半正則理想與Q0-Noether環

陳 丹, 王芳貴, 林詩雨

(四川師范大學 數學科學學院, 四川 成都 610066)

本文恒設R是交換環.眾所周知,在整環的環結構刻畫中,商域常常要發揮重要作用,所獲得的結論也非常豐富.因此,學者們希望把整環的環結構刻畫的方法和相關研究推廣到有零因子的交換環上.傳統地,人們以R的完全分式環T(R)(設S是環R的非零因子乘法封閉集,則T(R):=RS稱為R的完全分式環)的行為來代替整環時商域的行為.在實際應用中,T(R)的作用主要限于對正則理想的討論,即那些包含正則元的理想.例如,整環R是Dedekind整環,當且僅當R的非零理想是可逆理想,把Dedekind整環推廣到交換環時,自然地,學者們則把Dedekind環定義為滿足正則理想的可逆的交換環.

然而正則理想和T(R)在推廣整環上一些經典結果時,也存有不足之處.例如,設R是整環,則R是整閉整環(在R的商域中的整閉包即R自身)當且僅當多項式環R[x]是整閉整環.這一結果推廣到交換環時,Brewer等[1]注意到,“R在T(R)中整閉當且僅當R[x]在T(R[x])中整閉環”是不成立的,因而Lucas[2]關注了R的所謂有限分式環Q0(R),即由半正則理想構成的理想乘法系確定的環,這是R的一類比T(R)更大的擴環.借助Q0(R),Lucas[3]證明了若R是約化環,則R在Q0(R)中整閉當且僅當R[x]在T(R[X])中整閉.由此可見,當把整環上的某些結果推廣到交換環上時,Q0(R)的行為要好于T(R)的行為.

在文獻[3]中,Lucas首次借助R的有限生成半正則理想到R的同態等價類給出了有限分式環Q0(R)的構造.設I是R的理想,若I中包含R的一個非零因子,則I稱為正則理想;若存在I的有限生成子理想I0,使得ann(I0)=0,則I稱為R的半正則理想.相應地,理想I稱為R的非半正則理想,是指對I的任意的有限生成子理想J,都有ann(J)≠0.用表示R的有限生成半正則理想的集合.顯然是R的理想乘法系,即R∈,且對任意I,J∈,有IJ∈.設x表示R上的未定元.容易看到,設b0,b1,…,bn∈R,則理想I:=(b0,b1,…,bn)是半正則理想當且僅當多項式

f(x):=b0+b1x+…+bnxn

是R[x]的非零因子(參見文獻[4]).因此,Q0(R)更確切地可等價定義為

使得Iα?R},

其中T(R[x])表示多項式環R[x]的完全商環,即T(R[x])=R[x]S,這里S表示R[x]的非零因子乘法集.對α∈Q0(R),α也可以明確表示為

本文從對環R與環Q0(R)的相互關系進行對比研究入手,發現Q0(R)的許多性質集中表現在非半正則理想上.為了給出R的理想與環Q0(R)的理想的對比關系,引入了Lucas模和模的Lucas包絡概念,并證明了理想I的Lucas包絡Q0(I)≠Q0(R)當且僅當I是R的非半正則理想.作為應用,在第3節中也引入了Q0-Noether環的概念,即滿足非半正則理想升鏈條件的環,并證明了關于Q0-Noether環的Hilbert基定理,即R是Q0-Noether環當且僅當多項式環R[x1,x2,…,xn]是Q0-Noether環.

1 環Q0(R)和Lucas模

設M是R-模,定義

tor(M)={z∈M|存在J∈,使得Jz=0},

引理 1.1設M是R-模,f(x)∈R[x].若f(x)是M的零因子,則存在u∈M,u≠0,使得

f(x)u=0.

證明類似于文獻[4]中定理1.7.7的證明.

1)M是Lucas模;

Jz=f(J)=g(J)=Jy.

現在假設反之條件成立.對任何f:J→M,則存在同態g:R→E(M),使得對任何a∈J,有f(a)=g(a).記g(1)=z,則

Jz=g(J)=f(J)?M,

由條件有z∈M.因此,g:R→M是f的擴張,由命題1.4的1)有M是Lucas模.

命題 1.6設N是Lucas模,M是N的子模,則以下各條等價:

1)M是Lucas模;

證明1)?2) 設M是Lucas模,因為M?N,故可以假設E(M)?E(N).于是可記

E(N)=E(M)⊕A,

則有

z=y+a,y∈E(M),a∈A.

3)?2) 顯然.

稱之為M的Lucas包絡.

1)Q0(M)是Lucas模;

2) 若N是Lucas模,且M?N,則Q0(M)?N,于是Q0(M)是包含M的最小Lucas模;

3)M是Lucas模當且僅當Q0(M)=M;

4)Q0(Q0(M))=Q0(M);

5) 若A是M的子模,則Q0(A)?Q0(M).

證明1) 設Jz?Q0(M),其中

Jz?M?N.

注意到z∈E(M)?E(N),由命題1.5有z∈N.

3) 由2)即知.

4) 由3)即知.

5) 由于A?M?Q0(M)以及Q0(M)是Lucas模,由2)得到Q0(A)?Q0(M).

其中T(M[x])表示M[x]在R[x]的非零因子構成的乘法封閉集S下的局部化,即

T(M[x])=M[x]S.

顯然,H是R-模.

1) 設

2)Q0(M)=H.

證明1) 類似于文獻[4]中命題6.4.4的證明.

2) 先證明H是M的本性擴張,即H?E(M).

設

其中,ui∈M,i=0,1,…,n,α≠0,則

故

則

故

由dkα=uk,得到對任何i、k,有dkui=bkui=biuk,故Q0(M)?H,于是得到Q0(M)=H.

定義

于是Q0(M)作成了一個Q0(R)-模.特別地,Lucas模其實是Q0(R)-模.此外,若A是M的子模,則Q0(A)是Q0(M)的Q0(R)-子模.特別地,若I是R的理想,則Q0(I)是Q0(R)的理想.

下面給出Q0(R)的理想與R的理想的關系.

命題 1.101) 設J是R的有限生成半正則理想,則Q0(J)=Q0(R).特別地,若a∈R是非零因子,則Q0(Ra)=Q0(R).

3) 若I是R的非半正則理想,則Q0(I)是Q0(R)的非半正則理想.

4) 設a∈R,若a是R的零因子,則

Q0(Ra)?Q0(ann(ann(a))≠Q0(R).

證明1) 由J1?J,故1∈Q0(J).由于Q0(J)是Q0(R)的理想,對任意的r∈Q0(R),有r·1∈Q0(J),故Q0(R)?Q0(J),因此Q0(J)=Q0(R).特別地,a∈R是非零因子,因此ann(Ra)=0,Ra是R的有限生成半正則理想,則Q0(Ra)=Q0(R).

Q0(I)=Q0(R).

4) 因為Ra·ann(a)=0,因此

Ra?ann(ann(a)),

故有Ra?ann(ann(a))?R.從而

Q0(Ra)?Q0(ann(ann(a))≠Q0(R).

若有Q0(ann(ann(a))=Q0(R),則由命題1.10的2)知存在J∈,使得J?ann(ann(a)).于是對任何b∈ann(a),有Jb=0.由于J是半正則的,故b=0,即ann(a)=0,這與a是零因子的事實矛盾,故

Q0(ann(ann(a))≠Q0(R).

2 非半正則素理想

由命題1.10,環R與環Q0(R)之間的聯系主要依賴于非半正則理想,下面著重討論R的非半正則理想性質.

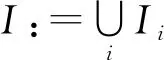
證明設N是I的有限生成子理想,則存在下標k,使得N?Ik.由于Ik是非正則的,故annR(N)≠0.因此,I是非半正則理想.

引理 2.21) 設I是R的非半正則理想,則存在R的極大的非半正則理想m,使得I?m.

2)R的極大的非半正則理想是素理想.

證明1) 對偏序集

Γ={A|A是R的非半正則理想,且I?A},

由于I∈Γ,故Γ非空.用集合的包含關系作為序關系,則Γ就做成了一個偏序集.設{Ai}是Γ中的一個鏈,由引理2.1可得A=∪Ai是R的非半正則理想.若A=R,因為R是半正則理想,故矛盾,則A≠R,且A∈Γ,故A是理想{Ai}的上界.由Zorn引理,存在R的極大的非半正則理想m,使得I?m.

命題 2.3設p是R的素理想,則以下各條等價:

1) p是R的非半正則理想;

2)Q0(p)是Q0(R)的素理想;

3)Q0(p)≠Q0(R);

4)Q0(p)是Q0(R)的非半正則理想;

5)Q0(p)∩R=p.

2)?3) 顯然.

3)?1) 由命題1.10即得.

1)?4) 由命題1.10的3)即得.

4)?3) 顯然.

5)?3) 顯然.

定理 2.4設I是R的非半正則理想,P是Q0(I)上的極小素理想,則P是Q0(R)的非半正則理想,且P=Q0(p),其中p=P∩R.

假設反之條件成立.設z∈M,令I=ann(z),對m∈-Max(R),由于在Mm中,故存在s∈R,s?m,使得sz=0,故Im.由引理2.2的1),I是半正則理想,故有J∈,使得J?I,于是有Jz=0,即M是-撓模.

命題 2.6對R-模M,以下各條等價:

2)?3) 0→A→F→M→0是正合列,其中F是自由模.由命題2.6的2)有F?Q0(A).

證明在命題2.6的3)中取A=N,F=Q0(N),M=Q0(N)/N即得.

3 Q0-Noether環

下面借助上節討論的非半正則理想來引入Q0-Noether環的概念,并討論其Hilbert基性質.

定義 3.1環R稱為Q0-Noether環,是指R的的任何非半正則理想的升鏈都是穩定的,即若

I1?I2?…?In?…

是R的非半正則理想升鏈,則存在正整數m,使得當m≥n時,恒有In=Im.

定理 3.2對環R,以下條件等價:

1)R是Q0-Noether環;

2)R有關于非半正則理想的極大條件,即R的任何非半正則理想的非空集合必有極大元;

3)R的任何非半正則理想都是有限生成的.

證明1)?2) 設Γ是R的任何非半正則理想的非空集合,反設Γ中無極大元,任取I1∈Γ,則I1不是極大元,因此有I2∈Γ,使得I1?I2.由于I2也不是極大元素,故存在I3∈Γ,使得I2?I3.如此進行下去,則在R中有一個不穩定的非半正則理想升鏈

I1?I2?I3?…?In?…

這與R是Q0-Noether環的事實矛盾.因此,反設不成立.

2)?3) 設I是R的非半正則理想,令

Γ={A?I|A是有限生成的}.

由于0∈Γ,故Γ非空.由假設條件2)知Γ有極大元A.若A≠N,則存在z∈I-A,于是A1=A+Rz是I的有限生成子理想,且真包含A.這與A的極大性矛盾,因此I=A是有限生成的.

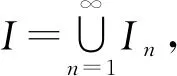
I=Rz1+Rz2+…+Rzk,z1,z2,…,zk∈I,

故存在一個m,使得zi∈Im,i=1,2,…,k.因此,有I=Im.于是當n≥m時,In=Im,故該升鏈是穩定的.

命題 3.3若R的有限生成半正則理想是正則理想,則R是Q0-Noether環當且僅當R滿足非正則理想的升鏈條件.

證明顯然正則理想都是半正則理想,從而非半正則理想都是非正則理想.由命題3.3的條件,有限生成半正則理想是正則理想,故半正則理想也是正則理想,從而非正則理想都是非半正則理想,故斷語為真.

命題 3.4設R是任何環,則在多項式環R[x]中,有限生成半正則理想是正則理想.

證明設A是R[x]的半正則理想,由文獻[4]中習題6.31(2),A中包含有非零因子,從而是正則理想.

結合命題3.3和命題3.4知,R[X]是Q0(R)-Noether環當且僅當R[x]滿足非正則理想的升鏈條件.下面證明關于Q0-Noether環的Hilbert基定理.

設A是R[x]的理想,用Ln(A)表示0與元素a的集合,其中a是某個n次多項式f∈A的首項,則Ln(A)是R的理想.

引理 3.5設A、B是R[x]的非零理想,則有:

1) 若i≤j,則Li(A)?Lj(A);

2) 若A?B,則對任何n,有Ln(A)?Ln(B);

3) 設A?B,則A=B當且僅當對任何n,有

Ln(A)=Ln(B).

證明參見文獻[10]的引理7.12.

引理 3.61) 設A是R[x]的非正則理想,則對任何m,Lm(A)是R的非半正則理想;

2) 設I是R的非半正則理想,則I[x]是R[x]的非正則理想.

證明1) 反設Lm(A)是半正則的,則存在一個半正則理想J=(d1,d2,…,dn)?Lm(A),于是有m次多項式f1,f2,…,fn∈A,使得fi的首項系數就是di,i=1,2,…,n.因為A是R[x]的理想,從而有

f=f1+xm+1f2+x2m+1f3+…+x(n-1)m+1fn∈A.

用c(f)表示f的系數生成的理想,則J?c(f).因此,c(f)是半正則的,故f是A中的非零因子.因為A是R[x]的非正則理想,A不含有非零因子,故矛盾.

2) 反設I[x]是正則理想,則I[x]有非零因子f.記f=anxn+…+a1x+a0,則ai∈I,且有

J:=(a0,a1,…,an)

是R的半正則理想,這與I是非半正則的假設矛盾.

定理 3.7(Hilbert基定理) 環R是Q0-Noether環當且僅當對任何n≥1,多項式環R[x1,x2,…,xn]是Q0-Noether環.

證明設R是Q0-Noether環,為證明多項式環R[x1,x2,…,xn]是Q0-Noether環,只需要對n=1的情形進行證明.由命題3.3與命題3.4,只要證明R[x]滿足非正則理想的升鏈條件即可.

設A1?A2?…?An?…是R[x]的非正則理想的升鏈,對任何m、n,由引理3.6,Lm(An)是R的非半正則理想.注意當i≤m,j≤n時,Li(Aj)?Lm(An),從而

L0(A0)?L1(A1)?L2(A2)?…

?Ln(An)?Ln+1(An+1)?…

是R的非半正則理想的升鏈.由于R是Q0-Noether環,故存在m,使得

Lm(Am)=Lm+1(Am+1)=…=

Lm+k(Am+k)=….

設i≥m且j≥m,取定k,使得i≤m+k,j≤m+k,由于

Lm(Am)?Li(Ak)?Lm+k(Am+k),

則有

Li(Aj)=Lm(Am).

對固定的i,Li(A0)?Li(A1)?…?Li(An)?…是R的非半正則理想升鏈,故存在mi,使得j≥mi時,有Li(Aj)=Li(Ami).

情形1i≥m,由前面的分析知取mi=m即能滿足要求;

情形2i

綜上可知mi有上界,設為k,于是當j≥k時,對一切i,恒有Li(Aj)=Li(Ak).由引理3.5的3),Aj=Ak,故給定的非正則理想升鏈是穩定的.因此,R[x]是Q0-Noether環.

反之,設多項式環R[x1,x2,…,xn]是Q0-Noether環,同樣只需要對n=1的情況進行證明,即設R[x]是Q0-Noether環.

設I1?I2?…?In?…是R的非半正則理想升鏈,由引理3.6的2)知

I1[x]?I2[x]?…?In[x]?…

是R[x]的非正則理想升鏈.由于R[x]是Q0-Noether環,則存在正整數m,使得當m≥n時,恒有In[x]=Im[x].自然地,當m≥n時,恒有In=Im,從而R是Q0-Noether環.

顯然Noether環是Q0-Noether環.

注 3.8Q0-Noether環不是Noether環是顯然的.例如,設R是整環,但不是Noether環,則R的非半正則理想只有零理想,從而R是Q0-Noether環,但R不是Noether環.