一類偽單調變分不等式的雙投影算法
楊登煉, 張 燕, 張永樂
(四川師范大學 數學科學學院, 四川 成都 610066)
設C?Rn是一個非空閉凸集,F:Rn→Rn是連續映射.經典變分不等式問題:尋找x*∈C使得
〈F(x*),x-x*〉≥0, ?x∈C,
(1)
其中〈·,·〉是歐幾里得內積.為了便于表述,將問題(1)及其解集分別記為VI(C,F)和S.變分不等式作為非線性分析中的重要分支,它在工程、交通、數學規劃等領域有廣泛應用.因此,如何構造算法來求解變分不等式問題是值得研究的,而投影算法是解變分不等式的一類相對簡單有效的方法,被廣泛研究[1-8].最早的投影算法由Goldstein[2]提出
xk+1=PC(xk-λF(xk)),
(2)
其中λ>0為步長.該算法對映射F的要求為強單調和L-Lipschitz連續.雖然該算法的每一步迭代只需要一次投影,但強單調條件不容易滿足,因此為了削弱F的強單調性,Korpelevich[3]提出了外梯度算法,其迭代形式為
yk=PC(xk-λF(xk)),
xk+1=PC(xk-λF(yk)).
(3)
在映射F滿足單調和Lipschitz連續的條件時得到了該算法的收斂性.在此基礎上,文獻[5]通過引入Armijo線性搜索來削弱F是L-Lipschitz連續性.1999年,Solodov等[6]給出了一種利用二次投影求解VI(C,F)的算法,該算法采用Armijo線性搜索來確定步長,文獻[7]說明了該算法能夠得到一個較優的步長,從而在理論上優于其他投影算法.文獻[6]的關鍵是在第二步投影中利用F(zk)構造了一個嚴格分離當前迭代點和解集的超平面,通過向該超平面與約束集的交上投影得到收斂到解的無窮迭代序列.2006年,He[8]利用F(zk)和rμ(xk)構造了一種新的超平面,進而提出了一種求解偽單調變分不等式的的雙投影算法,該算法具有較好的數值計算結果.隨后許多學者通過構造不同的超平面提出了不同的雙投影算法[9-11].受此啟發,本文利用F(zk)、F(xk)和rμ(xk)給出一類與以往不同的新的超平面,它能嚴格分離當前迭代點和解集,從而建立了一種新的雙投影算法.在映射F連續和偽單調條件下建立了算法的收斂性,進一步假設F是Lipschitz連續的,進行了收斂性分析.最后,數值實驗結果表明該算法是有效的.
1 基本準備
Rn是一個有限維的Hilbert空間,其內積和范數分別記為〈·,·〉和‖·‖.設C?Rn是一個非空閉凸集,對任意的z∈Rn,dist(z,C):=表示z到C的距離,
PC(z):=argmin{‖y-z‖|y∈C}
表示z在C上的投影,則有‖z-PC(z)‖=dist(z,C).對任意的μ>0,記rμ(x):=x-PC(x-μF(x)),稱rμ(x)為自然殘差函數.
定義 1.1設C?Rn是一個非空閉凸集.映射F:C→Rn,對任意的x,y∈C,若
1) 〈F(x)-F(y),x-y〉≥η‖x-y‖2,則稱F在C上是強單調的,其中η>0稱為F在C上的強單調系數.
2) 〈F(x)-F(y),x-y〉≥0,則稱F在C上是單調的.
3) 〈F(x),y-x〉≥0?〈F(y),y-x〉≥0,則稱F在C上是偽單調的.
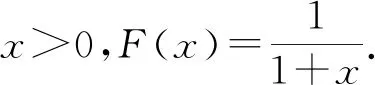
定義 1.2設C?Rn是一個非空閉凸集,映射F:C→Rn,任意x,y∈C,若
‖F(x)-F(y)‖≤L‖x-y‖,
則稱F在C上是L-Lipschitz連續的,其中L>0稱為F在C上的Lipschitz系數.
以下為本文定理證明中需要用到的引理.
引理 1.1[12]設C是Rn上的一個非空閉凸集,對任意的x∈Rn,PC(x)為x在C上的投影,則對任意的y∈C,有下列不等式成立:
1) 〈x-PC(x),y-PC(x)〉≤0;
2) ‖y-PC(x)‖2≤‖x-y‖2-‖x-PC(x)‖2.
引理 1.2[13]設C?Rn是一個非空閉凸集,給定參數μ>0,則x*∈S當且僅當rμ(x*)=0.
引理 1.3[8]對任意x∈C,〈F(x),rμ(x)〉≥μ-1‖rμ(x)‖2.
引理 1.4[8]設C是Rn上的非空閉凸集,h(x)是C上的θ-Lipschitz連續實函數,K={x∈C|h(x)≤0}.若Lipschitz系數θ>0,則對任意的x∈C,dist(x,K)≥θ-1max{h(x),0}.
引理 1.5[14]設tk>0且滿足
tk+1≤tk-βkt1+pk,βk≥0,p>0.
那么
tk≤t0(1+pt
特別的是,如果βk≡β,p=1,那么
t
2 主要結論
本文總假設以下條件成立:
(C1)S≠?;
(C2)F是連續和偽單調的.
2.1 雙投影算法下面敘述算法的具體內容.
算法 2.1選取初始點x0∈C,σ>0,μ∈(0,σ-1),γ∈(0,1),a≥0,b∈[0,μ-1].設k=0.
步驟1計算rμ(xk)=xk-PC(xk-μF(xk)),如果rμ(xk)=0,停止;否則,轉到步驟2.
步驟2計算zk=xk-ηkrμ(xk),其中ηk=γmk,mk是使得下面不等式成立的最小非負整數m,
〈F(xk)-F(xk-γmrμ(xk)),rμ(xk)〉≤
σ‖rμ(xk)‖2.
(4)
步驟3計算xk+1=PC∩Hk(xk),其中Hk:={v:hk(v)≤0},且函數
hk(v):=〈aF(xk)+F(zk)+bηkrμ(xk),
v-xk〉+(1-bμ)ηk〈F(zk),rμ(xk)〉+
b(1-μσ)ηk‖rμ(xk)‖2.
(5)
令k←k+1,轉到步驟1.
注 2.1關于構成超平面的函數hk(v),通過比較發現,本文構造的超平面與已有文獻中的超平面都不相同,并且包含某些已有超平面作為其特殊情形.如在文獻[9]中,
hk(v)=〈αηkrμ(xk)+βF(xk)+αμF(zk),
v-xk〉+αηk(1-μσ)‖rμ(xk)‖2,
hk(v)=〈F(xk)+F(zk),v-xk〉+
ηk〈F(zk),rμ(xk)〉,
它是(5)式中a=1和b=0的特殊情形,但反之不成立,因為文獻[11]中的超平面無‖rμ(xk)‖2這一項.
說明算法中(4)式是合理的.
引理 2.1對任意的k∈N+,當rμ(xk)≠0時,都存在非負整數m滿足(4)式.
證明假設這樣的m不存在,則存在k0∈N+,使得對所有的非負整數m,都有
〈F(xk0)-F(xk0-γmrμ(xk0)),rμ(xk0)〉>
σ‖rμ(xk0)‖2,
(6)
而F是連續的,且γ∈(0,1),則
〈F(xk0)-F(xk0-γmrμ(xk0)),
rμ(xk0)〉→0,m→∞.
由(6)式及σ>0可得矛盾式0<‖rμ(xk0)‖2≤0,則假設不成立,即存在非負整數m滿足(4)式.
其次證明算法2.1中的超平面能嚴格分離當前迭代點和變分不等式的解集.
引理 2.2設x*∈S,hk(v)如(5)式所示,則有如下不等式成立:
(i)hk(xk)≥(μ-1-σ)ηk‖rμ(xk)‖2,特別地,如果rμ(xk)≠0,則hk(xk)>0;
(ii)hk(x*)≤0.
證明由hk(v)的定義可得
hk(xk)=(1-bμ)ηk〈F(zk),rμ(xk)〉+
b(1-μσ)ηk‖rμ(x
(1-bμ)ηk(〈F(xk),rμ(xk)〉-
σ‖rμ(xk)‖2)+b(1-μσ)ηk‖rμ(x
(1-bμ)ηk(μ-1‖rμ(xk)‖2-σ‖rμ(xk)‖2)+
b(1-μσ)ηk‖rμ(xk)‖2=
(μ-1-σ)ηk‖rμ(xk)‖2,
其中(a)是因為(1-bμ)ηk≥0和(4)式,(b)由引理1.3可得.若rμ(xk)≠0,由于(μ-1-σ)ηk>0,則hk(xk)>0,(i)得證.
因為rμ(xk)=xk-PC(xk-μF(xk)),則xk-rμ(xk)=PC(xk-μF(xk)).對任意的x*∈S,根據引理1.1的1)可得
〈rμ(xk)-μF(xk),x*-xk+rμ(xk)〉≤0,
即
〈rμ(xk)-μF(xk),x*-xk〉≤
μ〈F(xk),rμ(xk)〉-‖rμ(xk)‖2.
從而有
〈rμ(xk),x*-xk〉=〈rμ(xk)-μF(xk),
x*-xk〉+μ〈F(xk),x*-x
〈rμ(xk)-μF(xk),x*-xk〉≤
μ〈F(xk),rμ(xk)〉-‖rμ(xk)‖2,
(7)
其中(c)由條件(C2)可得.于是有
hk(x*)=〈aF(xk)+F(zk)+bηkrμ(xk),
x*-xk〉+(1-bμ)ηk〈F(zk),rμ(xk)〉+
b(1-μσ)ηk‖rμ(xk)‖2=
a〈F(xk),x*-xk〉+〈F(zk),x*-xk〉+
bηk〈rμ(xk),x*-xk〉+
(1-bμ)ηk〈F(zk),rμ(xk)〉+
b(1-μσ)ηk‖rμ(x
〈F(zk),x*-xk〉+bηk〈rμ(xk),x*-xk〉+
(1-bμ)ηk〈F(zk),rμ(xk)〉+
b(1-μσ)ηk‖rμ(xk)‖2=
(〈F(zk),x*-zk〉+〈F(zk),zk-xk〉)+
bηk〈rμ(xk),x*-xk〉+
(1-bμ)ηk〈F(zk),rμ(xk)〉+
b(1-μσ)ηk‖rμ(x
〈F(zk),zk-xk〉+bηk〈rμ(xk),x*-xk〉+
(1-bμ)ηk〈F(zk),rμ(xk)〉+
b(1-μσ)ηk‖rμ(x
-ηk〈F(zk),rμ(xk)〉+bηk〈rμ(xk),
x*-xk〉+(1-bμ)ηk〈F(zk),rμ(xk)〉+
b(1-μσ)ηk‖rμ(xk)‖2=
bηk〈rμ(xk),x*-xk〉-bμηk〈F(zk),
rμ(xk)〉+b(1-μσ)ηk‖rμ(x
bηk(μ〈F(xk),rμ(xk)〉-‖rμ(xk)‖2)-
bμηk〈F(zk),rμ(xk)〉+
b(1-μσ)ηk‖rμ(xk)‖2=
bμηk(〈F(xk)-F(zk),rμ(xk)〉-
σ‖rμ(x
其中(d)和(e)由條件(C2)可得,(f)由zk=xk-ηkrμ(xk)可得,(g)由(4)式可得,(h)由(4)式可得.證畢.
2.2 收斂性與收斂率分析下面分別對算法2.1的收斂性以及收斂率進行分析.
定理 2.1假設條件(C1)~(C2)成立,則算法2.1在有限步終止或生成一個無限序列{xk}收斂到S.
證明總假設算法2.1生成無限序列,即對任意的k∈N+,rμ(xk)≠0.否則必存在k1∈N+,使得rμ(xk1)=0,則xk1∈S.即算法在有限步終止.
對任意的x*∈S,由xk+1=PC∩Hk(xk),根據引理1.1的2)得
‖xk+1-x*‖2≤‖xk-x*‖2-‖xk+1-xk‖2=
‖xk-x*‖2-dist2(xk,C∩Hk),
(8)
從而可得序列{‖xk-x*‖2}是收斂的,因此{xk}有界.同時由(8)式有
dist(xk,C∩Hk)=0.
(9)
因為F(x)和rμ(x)關于x是連續的,于是{F(xk)}和{rμ(xk)}都是有界序列,進而有{zk}和{F(zk)}有界,則存在一個常數0 ‖aF(xk)+F(zk)+bηkrμ(xk)‖≤M. 根據上式可知算法2.1中定義的hk(x)關于x在C上是Lipschitz連續的,且M為hk(x)的Lipschitz系數.于是由引理1.4以及xk?C∩Hk有 dist(xk,C∩Hk)≥M-1hk(xk), ?k∈N+. 結合上式以及引理2.2可得 dist(xk,C∩Hk)≥M-1hk(xk)≥ M-1(μ-1-σ)ηk‖rμ(xk)‖2, (10) σ‖rμ(xkj)‖2<〈F(xkj)- F(xkj-γkj-1rμ(xkj)),rμ(xkj)〉= 〈F(xkj)-F(xkj-γ-1ηkrμ(xkj)),rμ(xkj)〉≤ ‖F(xkj)-F(xkj-γ-1ηkrμ(xkj))‖‖rμ(xkj)‖, ?j∈N+. (11) 引理 2.3在定理2.1的假設條件下,進一步假設F是L-Lipschitz連續的,且存在常數α,δ>0以及任意的x,使得當rμ(x)≤δ時,有 dist(x,S)≤α‖rμ(x)‖, (12) 則存在常數β>0使得對充分大的k有 dist(x (13) 證明令η:=min先證明對任意的k∈N+,ηk>η成立.由ηk的構造可知ηk∈(0,1].若ηk=1,則顯然有于是可假設ηk<1,則有最小非負整數mk≥1使得ηk=γmk.根據mk的最小性以及映射F的Lipschitz連續性,有 σ‖rμ(xk)‖2< 〈F(xk)-F(xk-γ-1ηkrμ(xk)),rμ(xk)〉≤ ‖F(xk)-F(xk-γ-1ηkrμ(xk))‖‖rμ(xk)‖≤ Lγ-1ηk‖rμ(xk)‖2, 于是有ηk>L-1γσ≥η. 下證存在常數β>0使得對充分大的k,(13)式成立.設x*∈PS(xk),對于充分大的k,有以下不等式成立 dist2(xk+1,S)≤‖x ‖xk-x*‖2-dist2(xk,C∩H ‖xk-x*‖2-M-2(μ-1-σ)2ηk2‖rμ(xk)‖4≤ ‖xk-x*‖2-M-2(μ-1-σ)2η2‖rμ(x 其中(a)由(8)式可得,(b)由(10)式可得,(c)由(12)式可得.記β=M-2(μ-1-σ)2η2α-4,根據引理1.5可得到 dist(x (13)式得證.證畢. 本節給出數值實驗結果,在Windows 10,處理器為Intel(R) Core(TM)i5-4590 CPU@3.30 GHz的系統環境下,使用版本為R2019a的Matlab進行數值實驗.調用quadprog函數計算向非空閉凸集的投影.將本文的算法2.1與文獻[6]的算法2.2,文獻[10]的算法2.1和文獻[11]的算法3.1進行比較,并記錄計算機實驗結果.取‖rμ(x)‖≤10-4作為停機準則.x0表示初始點,nF表示計算F的次數,iter表示程序迭代的次數,time代表程序運行所需的時間. 例 3.1本例首先被文獻[15]測試.令C=[0,1]n,考慮映射F(x)=Mx+d,其中 分別選取x0=(0,0,…,0)和x0=(1,1,…,1)為初始點,且參數選取如下: 1) 文獻[6]的算法2.2:σ=0.3,γ=0.5,η-1=1,θ=4; 2) 文獻[10]的算法3.1:σ=2.5,γ=0.9,μ=0.2,α=β=1; 3) 文獻[11]的算法3.1:σ=6,γ=0.8,μ=0,15; 4) 算法2.1:σ=4,γ=0.8,μ=0.19,a=0.02,b=0.09. 前3種算法參數的選取與對應參考文獻中推薦的一致.數值結果分別見表1與表2. 表1 例3.1中初始點為x0=(0,0,…,0)各算法的數值結果 表2 例3.1中初始點為x0=(1,1,…,1)各算法的數值結果 例 3.2Kojima-Shindo非線性互補問題(n=4)被文獻[6]所考慮,其中函數F定義如下: F(x1,x2,x3,x4)= 其可行集為 文獻[10]的算法3.1中推薦的參數選取為σ=3,γ=0.9,μ=0.3,α=3,β=0.4.文獻[6]的算法2.2、文獻[11]的算法3.1和算法2.1推薦的參數選擇與例1相同.分別選取不同的初始點進行數值實驗,其結果見表3. 表3 例3.2中各算法的數值結果 通過數值實驗對比可以看出,在適當的參數選取下,本文中的算法較其他3種算法更快,這表明了本文中的算法在一定程度上的有效性.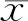
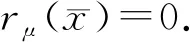
3 數值實驗