廣義Petersen圖的2-hued著色

劉鳳霞, 魏文娟

(新疆大學(xué) 數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院, 新疆 烏魯木齊 830046)

1 引言與基本概念

圖的著色理論是圖論重要的研究領(lǐng)域之一,其結(jié)論在工程領(lǐng)域中都有廣泛應(yīng)用.本文只考慮簡單有限圖,沒給出的術(shù)語和符號可參考文獻(xiàn)[1].

設(shè)

G=(V(G),E(G))

是一個圖,其中V(G)和E(G)分別表示圖的頂點集和邊集.頂點v∈V(G),圖G中與頂點v關(guān)聯(lián)的邊的數(shù)目稱為頂點v的度數(shù),記為dG(v).頂點集V(G)中所有與頂點v相鄰的頂點構(gòu)成的集合稱為頂點v的鄰集,即

NG(v)={u|uv∈E(G),u∈V(G)}.

閉鄰集記為

NG[v]=NG(v)∪{v}.

圖G稱為k-正則的,如果圖G中任意v∈V(G)都有

dG(v)=k.

頂點子集S?V(G)的導(dǎo)出子圖記為G[S].

圖的r-hued著色的定義早期是在文獻(xiàn)[2-3]中提出的.在文獻(xiàn)[4-5]中,r-hued著色又被稱為條件著色.特別地,當(dāng)r=2時,在文獻(xiàn)[4]中,2-hued著色被稱為動態(tài)著色.2008年,Li等[6]研究了條件著色的算法復(fù)雜性;2012年,林妍等[7]研究了r-hued著色的蟻群算法,并且給出廣義Petersen圖和其他一些圖類的這種算法，這使得研究條件著色更有意義.設(shè)k、r為正整數(shù),圖的一個(k,r)-著色是一個映射

φ:V(G)→C(k)={1,2,…,k}

滿足以下2個條件：

(i) 若uv∈E(G),則φ(u)≠φ(v)；

(ii) 任意v∈V(G),有

|φ(NG(v))|≥min{dG(v),r}.

圖的r-hued著色數(shù)是使得圖G具有(k,r)-著色的最小正整數(shù)k,記為χr(G).

廣義Petersen圖記為Pn,t,它的頂點集和邊集分別為:

V(G)={u1,u2,…,un;v1,v2,…,vn},

E(G)={uivi,uiui+1,vivi+t|1≤i≤n},

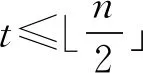
χ3(Pn,t)=4,

當(dāng)且僅當(dāng)n≡0(mod4),且t≡±1(mod4).

本文研究廣義Petersen圖的2-hued著色數(shù).由廣義Petersen圖定義知,廣義Petersen圖為3-正則圖.因此,要使得廣義Petersen圖滿足(k,2)-著色的條件,則任意頂點v∈V(G),|φ(NG(v))|≥2且φ(v)與其鄰點的著色不同,從而廣義Petersen圖的2-hued著色數(shù)χ2(Pn,t)≥3.關(guān)于圖著色的Brooks定理[10]指出,若G是連通的簡單圖,并且它既不是奇圈又不是完全圖，則

χ(G)≤Δ(G).

一般圖的r-hued著色數(shù)的上界也被深入研究，文獻(xiàn)[4]得到若G是Δ≤3的圖,則χ2(G)≤5,并且等式成立當(dāng)且僅當(dāng)G=C5,而廣義Petersen圖是3-正則圖且Pn,tC5,則χ2(Pn,t)≤4.因此

χ2(Pn,t)∈{3,4}.

關(guān)于一般圖的r-hued著色數(shù)的更多結(jié)論可查閱文獻(xiàn)[11-13].本文分別刻畫2-hued著色數(shù)為3或4的廣義Petersen圖.

2 主要結(jié)論及證明

廣義Petersen圖是一類重要的圖類,從文獻(xiàn)[14]中可以看出其在圖論研究中的重要作用.在廣義Petersen圖Pn,t中,設(shè)n與t的最大公約數(shù)為d,即(n,t)=d,則

V={v1,v2,…,vn}

定理 1若n≡0(mod3),t≡±1(mod3),則

χ2(Pn,t)=3.

證明已知χ2(Pn,t)≥3.下面構(gòu)造一個廣義Petersen圖Pn,t的(3,2)-著色φ.定義映射

φ:V(Pn,t)→{a,b,c}

如下：

φ-1(a)={ui,vj|i≡1(mod3),j≡0(mod3)},

φ-1(b)={ui,vj|i≡2(mod3),j≡1(mod3)},

φ-1(c)={ui,vj|i≡0(mod3),j≡2(mod3)}.

因為n≡0(mod3),對任意ui∈{u1,u2,…,un},有

φ({ui-1,ui,ui+1})={a,b,c},

所以

|φ(NG(ui))|≥2.

對任意uivi∈E(G),有

φ(ui)≠φ(vi).

對任意vi∈{v1,v2,…,vn},當(dāng)t≡1(mod3)時,有:

φ(vi+t)=φ(vi+1),φ(vi-t)=φ(vi-1);

當(dāng)t≡-1(mod3)時,有:

φ(vi+t)=φ(vi+2)=φ(vi-1),

φ(vi-t)=φ(vi-2)=φ(vi+1).

因此

φ({vi,vi-t,vi+t})={a,b,c},

從而對任意vi∈{v1,v2,…,vn},有

|φ(NG(vi))|=2,

故φ是廣義Petersen圖Pn,t的一個(3,2)-著色,所以χ2(Pn,t)≤3.進(jìn)一步,χ2(Pn,t)=3.綜上所述,定理1得證.

由定理1,當(dāng)n≡0(mod3)時,廣義Petersen圖Pn,t的2-hued著色數(shù)只剩t≡0(mod3)的情況沒有刻畫.下面這個定理將得到當(dāng)n≡0(mod3)且t=3時,廣義Petersen圖的2-hued著色數(shù).

定理 2若n≡0(mod3),t=3,則χ2(Pn,t)=3.

證明構(gòu)造廣義Petersen圖Pn,t的一個(3,2)-著色φ.

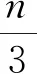
φ:V(Pn,t)→{a,b,c}

如下：

φ-1(a)={ui,vj|i≡1(mod3),

j≡5(mod6),j≡0(mod6)};

φ-1(b)={ui,vj|i≡2(mod3),

j≡3(mod6),j≡4(mod6)};

φ-1(c)={ui,vj|i≡0(mod3),

j≡1(mod6),j≡2(mod6)}.

因為n≡0(mod3),所以由上述映射得對任意ui∈{u1,u2,…,un},有

φ({ui-1,ui,ui+1})={a,b,c},

故

|φ(NG(ui))|≥2.

進(jìn)一步,對任意uivi∈E(G),有

φ(ui)≠φ(vi).

因為n≡0(mod3)且是偶數(shù),所以對任意vi∈{v1,v2,…,vn},由映射得

φ(vi-3)=φ(vi+3).

又因為

φ(ui)≠φ(vi),

φ(ui)=φ(ui-3)=φ(ui+3),

所以

φ({vi,vi-t,vi+t,ui})={a,b,c},

從而對任意vi∈{v1,v2,…,vn},有

|φ(NG(vi))|≥2.

因此,在這種情況下,φ是廣義Petersen圖Pn,t的一個(3,2)-著色.

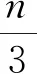
φ:V(Pn,t)→{a,b,c}

如下：

φ-1(a)={ui,vj|i,j≤n-6,i≡1(mod3),

j≡3(mod6),j≡5(mod6)};

φ-1(b)={ui,vj|i,j≤n-6,i≡2(mod3),

j≡0(mod6),j≡4(mod6)};

φ-1(c)={ui,vj|i,j≤n-6,i≡0(mod3),

j≡1(mod6),j≡2(mod6)}.

外圈剩余頂點un-5,…,un-1,un分別著色為b、c、a、c、a、b;里圈剩余頂點vn-5,…,vn-1,vn分別著色為a、a、b、b、b、c.因為頂點u1,u2,…,un-7,un-6用a、b、c循環(huán)著色,所以對頂點ui,2≤i≤n-7,有

φ({ui-1,ui,ui+1})={a,b,c},

從而|φ(NG(ui))|≥2.又因為

φ(u1)=a,φ(un)=b,

φ(u2)=b,φ(v1)=c,

所以

|φ(NG(u1))|=2.

同理可得

|φ(NG(ui))|=2,n-6≤i≤n.

由映射可得:

φ(vi-3)=φ(vi+3),φ(vi)≠φ(ui),

φ(ui)=φ(ui+3)=φ(ui-3).

因此,對任意vi∈{v4,v5,…,vn-9}有

φ({vi,vi-3,vi+3,ui})={a,b,c},

所以

|φ(NG(vi))|≥2.

又因為

φ(v1)=c,φ(vn-2)=b,

φ(v4)=b,φ(u1)=a,

所以

|φ(NG(v1))|=2.

同理可得

|φ(NG(vi))|=2, 2≤i≤3或者n-8≤i≤n.

因此,在這種情況下,φ是廣義Petersen圖Pn,t的一個(3,2)-著色.

綜上所述,當(dāng)n≠0(mod3),t=3時,Pn,t有一個(3,2)-著色.又因為χ2(Pn,t)≥3,即得

χ2(Pn,t)=3.

定理2得證.

由定理1知,當(dāng)n≡0(mod3),t≡±1(mod3)時,證明χ2(Pn,t)=3.由定理2,當(dāng)n≡0(mod3)時,證明當(dāng)t=3時,χ2(Pn,t)=3.對于t=6,9,…的情況,本文沒有完整刻畫出來,但下面的定理說明當(dāng)n≡0(mod3),t=6,9,…時的部分情況.

定理 3若n=mt,m≡0(mod3),t≡0(mod3),則χ2(Pn,t)=3.

證明因為(n,t)=t,則V={v1,v2,…,vn}導(dǎo)出的子圖G[V]是t個不交的m階圈.下面構(gòu)造廣義Petersen圖Pn,t的一個(3,2)-著色φ.定義映射φ:V(Pn,t)→{a,b,c}如下：

φ-1(a)={vft+i|1≤i≤t,

f=0,3,6,…,m-3};

φ-1(b)={vft+i|1≤i≤t,

f=1,4,7,…,m-2};

φ-1(c)={vft+i|1≤i≤t,

f=2,5,8,…,m-1}.

外圈頂點uft+1,uft+2,…,uft+t,當(dāng)f=0,3,6,…,m-3時,分別用b、c、b、c循環(huán)著色；當(dāng)f=1,4,7,…,m-2時,分別用a、c、a、c循環(huán)著色；當(dāng)f=2,5,8,…,m-1時,分別用b、a、b、a循環(huán)著色.

因為m≡0(mod3),t≡0(mod3),所以由映射可得

φ({vi-t,vi,vi+t})={a,b,c}.

因此

|φ(NG(vi))|≥2.

對于外圈頂點uft+2,…,uft+t-1,由著色過程可知

φ(uft+j)≠φ(vft+j),

φ(uft+t)≠φ(uft+t-1),

φ(uft+j+1)≠φ(uft+j),j=1,2,…,t-1,

所以對任意ui∈{uft+1,uft+2,…,uft+t},有

|φ(NG(ui))|≥2.

因此,φ是廣義Petersen圖Pn,t的一個(3,2)-著色.

綜上所述,在這種情況下,χ2(Pn,t)≤3,又因為χ2(Pn,t)≥3,即得χ2(Pn,t)=3.定理得證.

由已知結(jié)論,知道廣義Petersen圖的2-hued著色數(shù)是3或4,本文接下來刻畫2-hued著色數(shù)是4的廣義Petersen圖.

定理 4若n≠0(mod3),則χ2(Pn,1)=4.

證明廣義Petersen圖是3-正則圖,且

χ2(Pn,t)≤4.

只需證

χ2(Pn,t)≥4.

下面證明,對于Pn,1找不到一個(3,2)-著色.設(shè)存在φ:V(Pn,1)→{a,b,c}是Pn,1的一個(3,2)-著色.由于對稱性,不妨設(shè)

φ(u1)=a,φ(u2)=b.

情形1φ(v1)=c,則由(3,2)-著色的定義知

φ(v2)≠φ(v1)

且

φ(v2)≠φ(u2),

所以φ(v2)=a.進(jìn)一步,因為

|φ(NG(u2))|≥2,

故φ(u3)=c.又因為

φ(v3)≠φ(v2)=a,

φ(v3)≠φ(u3)=c,

所以φ(v3)=b.按上述著色過程可得:

φ-1(a)={ui,vj|i≡1(mod3),j≡2(mod3)};

φ-1(b)={ui,vj|i≡2(mod3),j≡0(mod3)};

φ-1(c)={ui,vj|i≡0(mod3),j≡1(mod3)}.

具體著色如圖1所示.當(dāng)n≡1(mod3)時,有

圖1 廣義Petersen圖Pn,1且φ(v1)=c

φ(un)=a,

而φ(u1)=a且u1un∈E(Pn,1),矛盾.當(dāng)n≡2(mod3)時,有φ(vn)=a,而φ(v2)=a,φ(u1)=a,則|φ(NG(v1))|=1,矛盾.

情形2φ(v1)=b,則由

|φ(NG(u1))|≥2,

得

φ(un)=c.

因為φ(vn)≠φ(v1)且φ(vn)≠φ(un),則φ(vn)=a.按上述著色過程可得φ(un-1)=b,φ(vn-1)=c,….觀察知,外圈頂點u2,u1,un,un-1,…,u4,u3按照b、a、c循環(huán)著色;里圈頂點v1,vn,vn-1,…,v3,v2按照b、a、c循環(huán)著色,具體著色如圖2所示.當(dāng)n≡1(mod3)時,有φ(u3)=b,而φ(u2)=b且u2u3∈E(Pn,1),矛盾.當(dāng)n≡2(mod3)時,φ(v3)=b,φ(v1)=b,且φ(u2)=b,則|φ(NG(v2))|=1,矛盾.

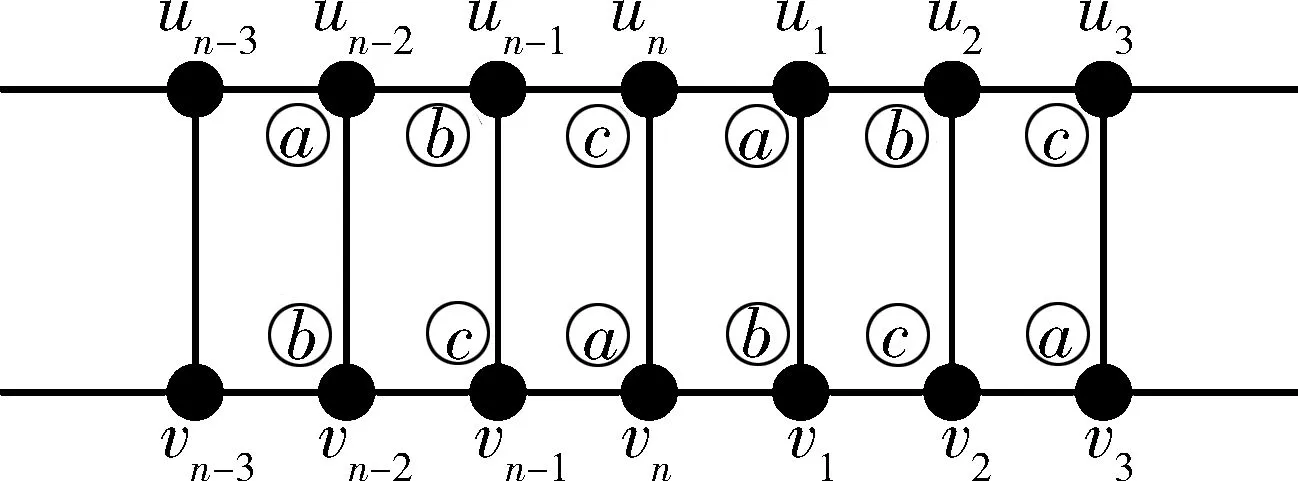
圖2 廣義Petersen圖Pn,1且φ(v1)=b

綜上所述,當(dāng)n≠0(mod3)時,χ2(Pn,1)>3.又因為χ2(Pn,1)≤4,故

χ2(Pn,1)=4.

定理1和定理2刻畫n≡0(mod3)的廣義Petersen圖的2-hued著色數(shù).當(dāng)n≠0(mod3)時,由定理4,證明得χ2(Pn,1)=4.但是本文只考慮t=1時的情況,對于t的其他情況,猜測χ2(Pn,t)=4.