三階非線性薛定諤方程新的精確解
劉靜靜, 曹 彧, 孫峪懷
(四川師范大學 數學科學學院, 四川 成都 610066)
非線性薛定諤方程是量子力學的基本方程.這里,討論如下形式的三階非線性薛定諤方程[1-4]
iqx+α2(qtt+2q|q|2)-iα3(qttt+
6qt|q|2)=0,
(1)
其中i是虛數單位,i2=-1,x表示沿傳播方向的歸一化距離,t表示延遲時間,q=q(x,t)表示電場的緩變包絡線,α2、α3是實參數.對非線性薛定諤方程,已經有很多求解方法,例如:修正的簡單方程方法[5]、拉格朗日恒等式法[6]、tan(φ(ξ)/2)展開法[7]、變分法[8]以及文獻[9-12]給出的方法.特別地,一些學者對三階非線性薛定諤方程的精確解進行了研究,例如,Liu等[1]通過Hirota雙線性法,Zkan等[13]通過擴展的修正子方程方法與Lie對稱群方法分別求得了三階非線性薛定諤方程的精確解.本文通過動力系統分支理論[14-18],試圖分析了此三階非線性薛定諤方程的演化規律,構建了其精確解及一些解所對應的圖像,具體過程與結果如下.
1 求解過程
將方程(1)表示成如下形式:
q(x,t)=u(ξ)eiφ(x,t),ξ=x-vt,
φ=-kx+wt+θ,
(2)
其中,u和φ分別代表q的振幅分量和相位分量,v和k分別代表孤子速度和波矢,w是頻率,θ是相位常數.現將方程(2)帶入方程(1),分離實部虛部得
(3)
α3u?v3+u′+(6α3u2u′-
2α2wu′-3α3w2u′)v=0.
(4)
對方程(4)積分一次并令其積分常數為0,可得
(5)
比較方程(3)和(5)得到
(6)
其中參數滿足如下條件:
對于(5)式,令u′=y,可得如下Hamilton系統:
(8)
以及Hamilton量
(9)
其中
為了得到(8)式平面相圖,令
f(u)=-Au3+Bu.
(10)
1) 當AB>0,得到f(u)的3個零點
(11)
零點處的Hamilton量分別為:
h1=H(u1,0)=0,h2=H(u0,0)=
(12)
2) 當AB<0,得到f(u)的一個零點
u3=0.
(13)
假設Si(ui,0)(i=0,1,2)是系統(8)的一個平衡點,則該平衡點處的特征值為
(14)
由動力系統定性理論可得:
1) 當f′(ui)>0時,則平衡點Si(ui,0)是鞍點;
2) 當f′(ui)=0時,則平衡點Si(ui,0)是退化的鞍點;
3) 當f′(ui)<0時,則平衡點Si(ui,0)是中心點.
由上述定理,根據系數A,B可得到系統(8)不同的分支相圖,如圖1~2所示.
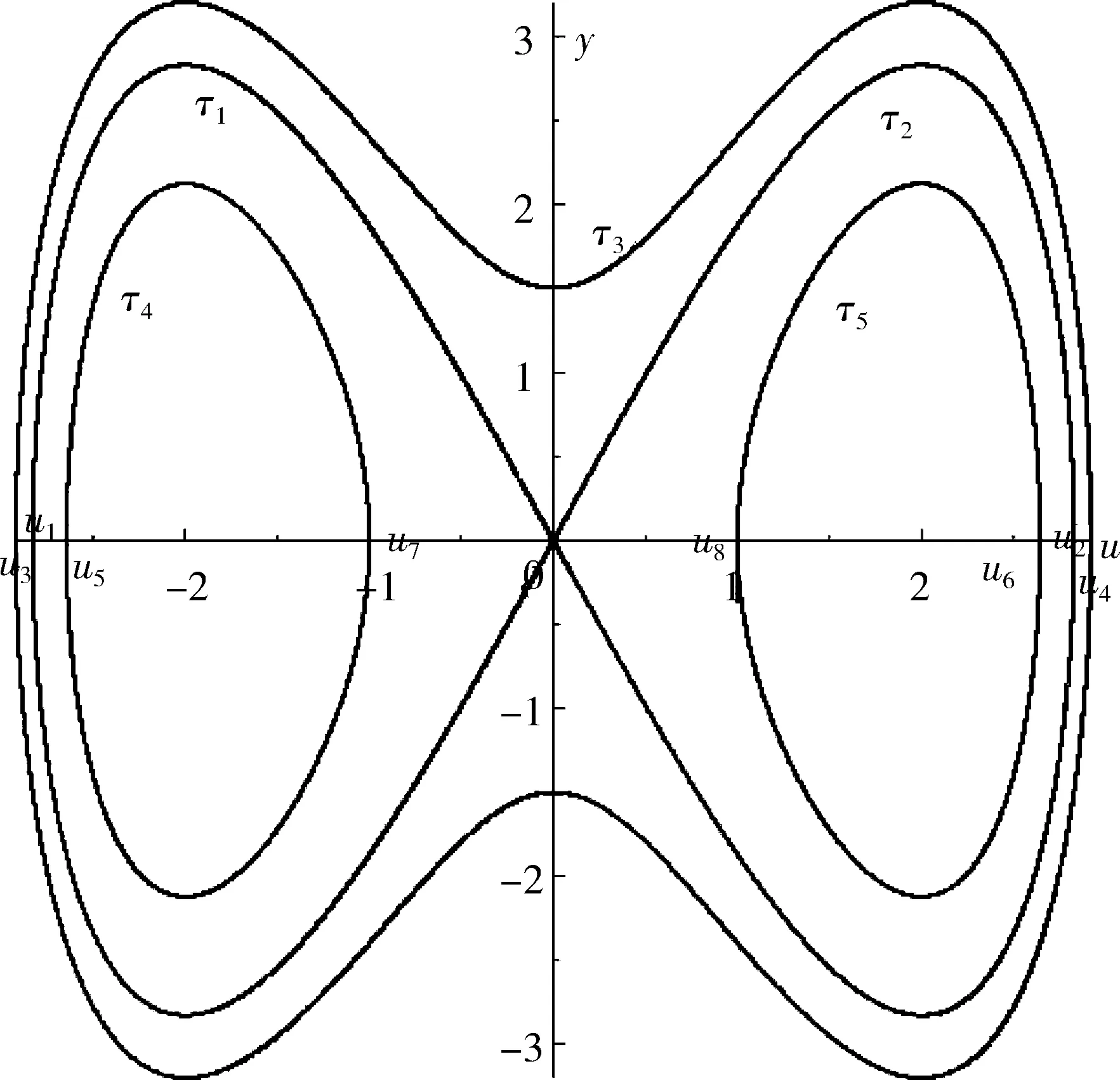
圖1 當A>0,B>0時,系統(8)的分支相圖

圖2 當A>0,B<0時,系統(8)的分支相圖
由圖1知,當A>0,B>0時,系統(8)有一個唯一平衡點.
是中心點,原點(u0,0)=(0,0)是鞍點.
情況 1當h=h1=0,由過點(u1,0)、(u2,0)、(0,0)的軌道τ1、τ2:
(15)
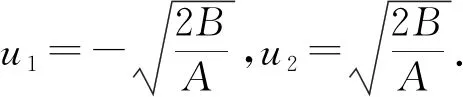
求解并化簡得
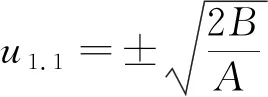
(17)
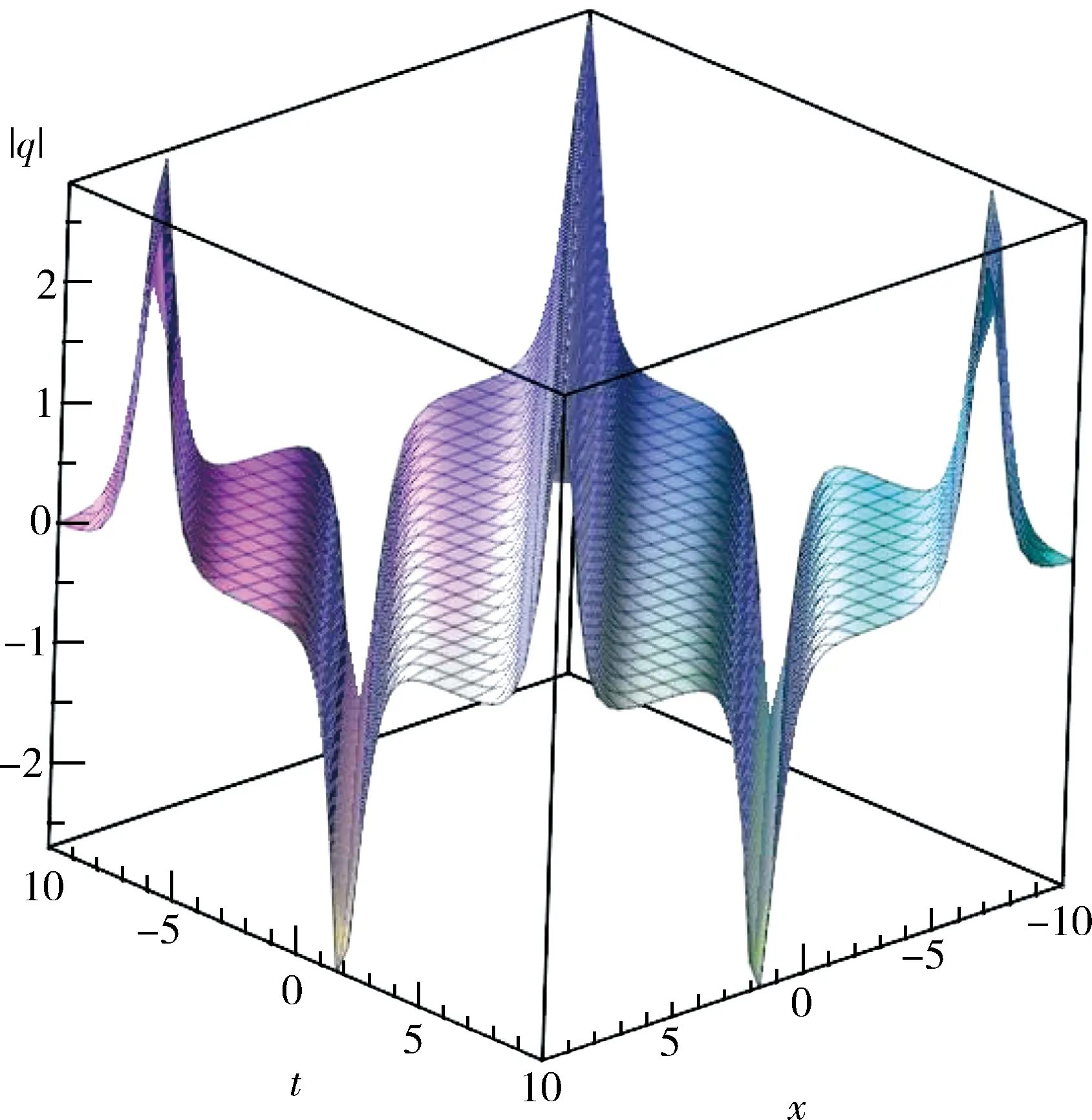
即得到方程(1)的亮孤立波解
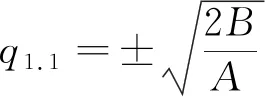
exp[i(-kx+wt+θ)],
(18)
其中
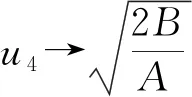
當參數A=1,B=4,c=1,-10 圖3 A=1,B=4,v=1,-10 情況 2當h>h1=0,由過點(u3,0)、(u4,0)軌道 τ3:y= 其中 (20) 求解并化簡得: (21) 其中 即得到方程(1)的周期波解: 其中 r1= exp[i(-kx+ωt+θ)]. (23) 圖 -10 圖 -10 圖-10 τ4,τ5:y= 其中, (25) 求解并化簡得: (26) exp[i(-kx+wt+θ)], (27) 其中 為進一步分析、理解和構建光纖傳輸中的孤波的演化,首先通過波變換將三階非線性Schr?dinger方程化為平面動力系統,進而分析出奇點及其分類、演化軌道.同時還得到系統色散關系和哈密頓量.沿不同演化軌道積分,構建了系列精確解.通過與先前文獻[1,13]結果的比較,發現q2.1、q2.2、q3.1、q3.2結果是新的孤立波.研究過程與結果表明,上述方法對求解其他類型的薛定諤方程具有普適性.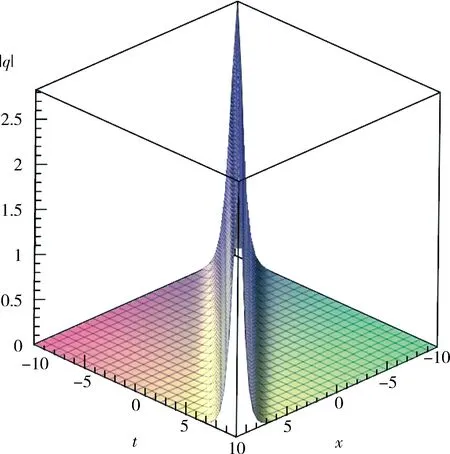
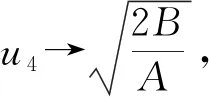
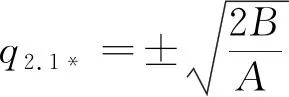


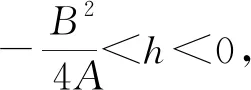

2 總結與討論

