基于卷積神經網絡的算法選擇研究

林秀麗, 李均利, 田竟民, 程小帆

(四川師范大學 計算機科學學院, 四川 成都 610101)

1 準備知識

受自然界生物進化機制和群體行為的啟發,許多元啟發式算法在過去幾十年中得到了廣泛的發展和應用,如遺傳算法[1-2]、模擬退火算法[3]、差分進化算法[4]、粒子群算法[5]、人工魚群算法[6]、人工蜂群算法[7]、蟻群算法[8]、灰狼優化算法[9]和螢火蟲算法[10]等.以上這些算法是不依賴于問題特征的高級算法,在解決各種復雜的優化問題上能達到優異的效果.然而,正如“沒有免費的午餐定理”[11]中所提到的：并不存在一個與具體無關的、普遍適用的通用型算法能夠解決所有的優化問題.因此,對于不同類型的問題,仍然需要不同的算法.這時,人們開始針對特定問題研發合適的算法[12-13].但是專用的算法設計需要不同領域的知識,很難為不同領域的問題開發新的算法.另外,通過進行大量實驗來選擇現有的最佳算法是也不切實際的,因為許多工業優化問題計算成本很高[14-15].目前最為常見的算法選擇方法是基于經驗進行的[16],實際上,算法選擇問題仍沒有根本解決.

為了解決算法選擇問題,Rice[17]提出了算法選擇概念框架,通過研究問題特征與算法之間的關系,從給定問題中獲取問題特征,找到特征與算法之間的映射關系.在此理論基礎之上,研究者們將算法選擇看作是一個學習的過程,并應用在機器學習領域,形成了元學習基本思想.元學習的基本思想是由Vilalta和Drissi[18]提出的,描述了分類問題的特征并驗證其特征對算法的影響.Smith-Miles[19]提出了基于元學習的算法選擇框架,將該方案快速拓展到了其他領域,其中包括時間序列的預測問題、回歸問題、排序問題、約束問題和優化問題等.Hutter等[20]提出適用于NP難題的算法選擇和配置的自動化技術.崔建雙等[21]基于Rice模型和元學習推薦的優化算法提出了組合優化問題算法自動選擇框架.在元學習思想基礎框架下,研究者們將算法選擇作為一個算法分類任務,并在機器學習算法上進行驗證,其中,Koch等[22]采用單側的支持向量回歸的方法幫助算法選擇.最近,深度學習的方法在各個領域興起[23],當然也有研究者采用深度學習方法解決算法選擇問題.如Kerschke等[24]將機器學習與探索性景觀特征相結合,提出自動構建優化問題的算法選擇模型,但該方法只針對單目標的連續黑盒優化問題.在此基礎之上,He等[25]提出從優化問題中提取特征信息并保存為二維圖像的方法,利用卷積神經網絡(VGG)對黑盒測試問題進行分類和選擇.Muoz等[26]試圖利用神經網絡來預測協方差自適應進化策略算法(CMA-ES)的性能,但是由于輸入的大小和能夠訓練參數的數量都比較小,該方法不能完全體現深度神經網絡的性能.雖然對約束滿足問題的算法選擇已經做了很多研究,但在單目標的無約束優化問題上卻很少有工作關注將深度學習模型應用于算法選擇問題.為了填補這一空白,本文將提出從優化問題中提取景觀信息的方法,并使用卷積神經網絡來學習這些景觀特征信息.

針對以上問題,本文提出了基于深度學習的算法選擇框架,即一個可以將深度學習應用于算法選擇問題的整體框架.在本框架中利用卷積神經網絡方法作為算法選擇問題的訓練和預測工具.

本文的安排如下:第2部分提出基于深度學習的算法選擇框架;第3部分介紹產生問題實例樣本的基準問題生成器;第4部分介紹基于卷積神經網絡算法選擇問題模型和設計;第5部分對算法選擇問題進行實驗,并對實驗結果進行分析;最后,對本文工作進行簡要總結以及對未來工作的展望.

2 基于深度學習的算法選擇框架

2.1 基于Rice的算法選擇算法選擇解決的主要問題是：對于待解決的問題,在已知算法上進行搜索,尋找效果最好的算法,即最佳匹配算法.1976年Rice首次提出了算法選擇問題的抽象模型,具體模型如圖1所示.

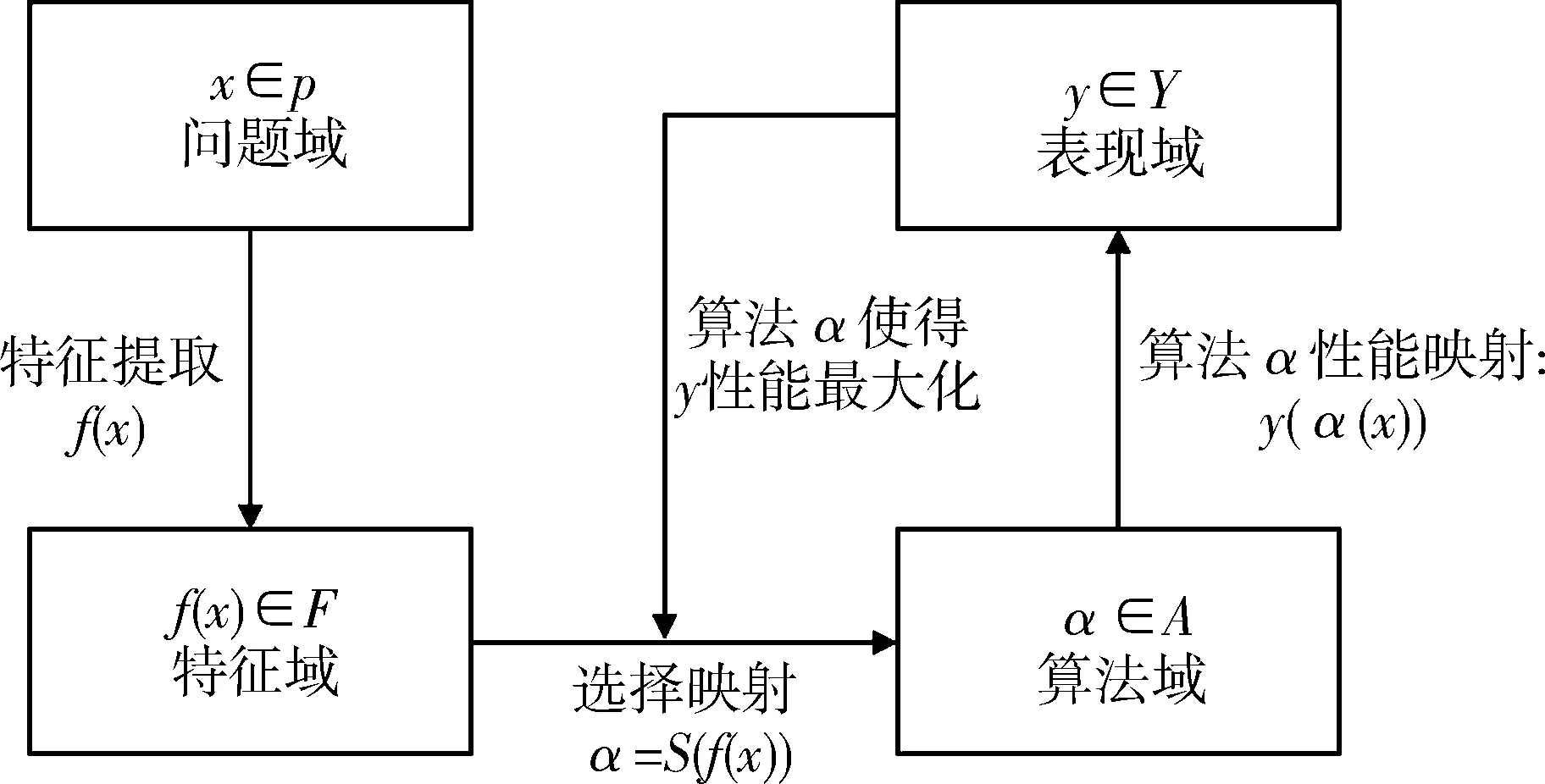
圖1 Rice算法選擇抽象模型

2.2 基于深度學習的算法選擇框架以Rice提出的算法選擇抽象模型為原型,本文提出基于深度學習的算法選擇框架,如圖2所示,其中算法選擇框架主要包含：問題域(P)、算法域(A)和表現域(Y).由于“特征域”是最難定義、最難選擇、最難提取的,而卷積神經網絡相較于傳統手工特征提取的方法最大的優點是它在學習過程中自動提取數據的主要特征,所以本文采用卷積神經網絡對問題特征進行自動提取,跳過了特征域的問題.

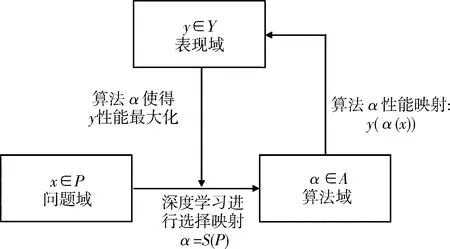
圖2 基于深度學習的算法選擇框架

基于深度學習的算法選擇過程如下：首先利用基準問題生成器,產生大量的問題實例樣本,將這些問題實例集作為訓練集.然后,采用深度學習中的學習方法進行特征學習,獲取問題特征與算法性能相對應的表現域.

基于深度學習的算法選擇過程實現步驟如下：

1) 通過收集或生成問題實例數據集;

2) 設計神經網絡模型;

3) 利用神經網絡訓練出算法選擇模型;

4) 將訓練好的算法選擇神經網絡模型預測新的數據集,驗證準確率并做出評價.

3 基準問題生成器(HFEBG)

由于本文采用卷積神經網絡實現算法選擇問題,需要大量數據對模型進行訓練.基準問題生成器能夠產生大量的基準優化問題.基準問題是標準優化的問題,應用于優化算法的估計、表現特征和性能度量.一般情況下,常用的基準問題有4類：

2) 在有影響力的文章中所使用的知名基準問題,如文獻[29];

3) 可調基準生成器,如最大集合高斯(MSG)景觀生成器[30];

4) 現實中優化問題[31].

本文采用Lou等[32-34]提出的基于層次適應度的基準問題生成器(HFEBG)生成滿足本實驗要求的訓練樣本.HFEBG的目的是找到在算法A1上表現最佳的問題實例(UE-A1),其中算法

A1∈SA={A1,A2,…,An}.

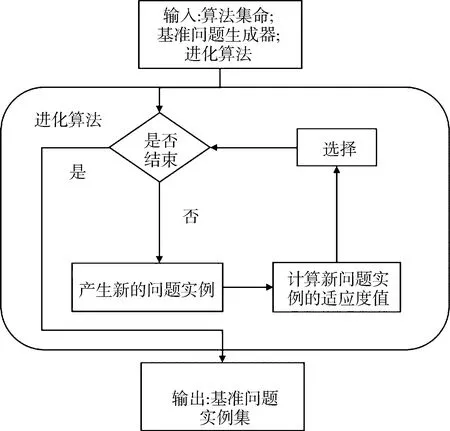
圖3 HFEBG產生問題實例流程

HFEBG通過輸入一組算法集合,可調基準問題生成器和進化問題實例的進化算法.最后輸出滿足條件的結果,即問題實例.HFEBG中采用最大集合高斯測試問題生成器(MSG)作為基準問題生成器.問題實例I由5個參數組成,分別是問題維度(d)、局部最優值的數量(n)、每個局部最優值的標準差σ(n*1)、在局部最優值的每個維度下的壓縮率Q(n*d)和局部最優值與全局最優值的比值r.通常問題維數d=d0和局部最優值個數n=n0都是固定的,于是問題實例I可以表示為

I=MSG(d0,n0)(x),

其中

x={σ,Q,r}.

I*=HFEBGDE(MSG(d0,n0)(x*)).

于是本文的問題實例的由3部分組成,分別是標準差、壓縮率和全局最優值和局部最優值的比值.

4 卷積神經網絡

4.1 卷積神經網絡卷積神經網絡[35]主要由3部分組成,分別是卷積層、池化層和全連接層.卷積層提取特征,池化層進行降維操作,全連接層完成分類輸出.具體操作如下：

1) 卷積層.卷積層主要是通過卷積核對輸入數據進行特征提取操作.卷積核的大小和數量對整個網絡的性能起著關鍵性的作用.卷積核的個數與網絡的整體性能是成正比的,但是一旦卷積核的個數增加(同時也在增加計算的規模)到一定的值后,性能的提升就微乎其微.因此,卷積核數量的設計對于不同的分類任務就會設置不同的參數.卷積計算公式為

i=1,2,…,q，

(1)

通常在卷積操作過后,會使用激活函數實現函數的非線性變換.常用的激活函數有Sigmoid、Tanh、ReLU和Maxout.卷積神經網絡中使用頻率最多的激活函數為ReLU,其表達式為

y(i)=f(g(i))=max{0,g(i)},

i=1,2,…,q.

(2)

該激活函數的作用是將所有非零數值都映射為0,將大于0的數值不變，其中g(i)表示ReLU的輸入數據,f(g(i))是ReLU的輸出數據.

2) 池化層.在卷積層后采用池化層(也稱采樣層),不僅降低了提取的特征的維數,也降低計算規模,還對特征提供基本的平移不變性.雖然池化層有以上這些好處,但池化的比例要適中,若池化的比例過大,大量的數據特征丟失,也會迫使網絡性能下降.常見的池化方法包括均值池化、最大池化等.具體池化計算公式為

p

j=1,2,…,q,

(3)

3) 全連接層.在卷積層和池化層之后,最后采用全連接層來完成分類任務.全連接層通常和激活函數一起使用.在處理兩分類問題時,輸出層一般采用Sigmod函數作為激活函數；處理多分類問題時采用Softmax函數.本實驗采用Softmax函數,函數將多個神經元的輸出映射到[0,1]區間內,輸出概率作為分類的結果.具體激活函數為

σ(z)

(4)

4.2 基于卷積神經網絡的算法選擇問題模型設計用于解決算法選擇問題的卷積神經網絡的整體架構由6個卷積層、6個歸一化層、一個池化層、一個輸出層(Dropout)和一個全連接層組成.考慮到本文中問題實例結構為向量形式,故卷積核大小設置為向量,總體框架設計如圖4所示,具體網絡參數設置如表1所示.

圖4 算法選擇問題神經網絡模型

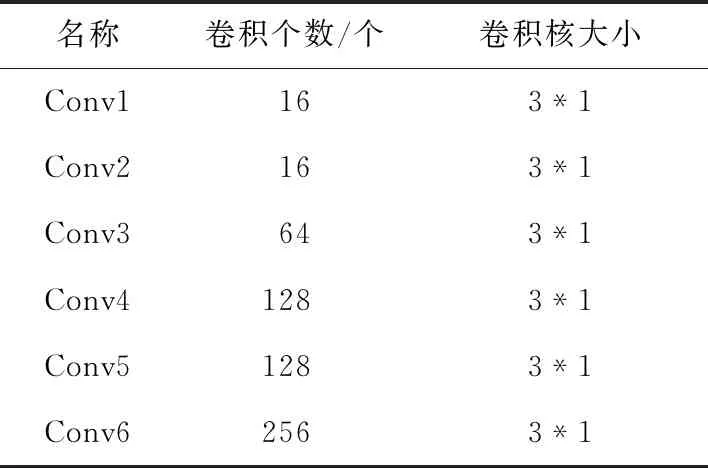
表1 算法選擇問題模型結構參數

為了使分類的效果達到最佳,特地對卷積神經網絡模型中參數的設置以及層次的安排做出一些調整.

首先,在每個卷積操作之后添加ReLU作為激活函數.另外,也在每一個卷積層后采用了批處理歸一化(BN)操作.批處理歸一化操作通過規范化使得每一個層的網絡輸入數據的均值和方差都在一定的范圍內,允許每一個層進行獨立的學習,提高整個神經網絡的學習速度.當學習率參數更新過大時,使用批處理歸一化操作就不會受到參數值大小的影響.另外還能夠有效緩解梯度消失等問題.

其次,還添加了Dropout層、L2歸一化方法和最大池化層.池化層用于減少輸出特征圖的大小和加快模型訓練的速度,而Dropout層能夠讓一維卷積神經網絡模型避免出現過度擬合的情況.

最后,利用Softmax函數將分類問題輸出.Softmax層的輸出數目等于分類個數.例如,如果是從3個算法組成的算法集中為給定的問題推薦一個合適的算法,那么該任務中Softmax層的輸出數應該是3.Softmax層采用交叉熵損失對分類誤差進行評估.交叉熵損失公式為

Losslog

(1-pi)log

(5)

5 實驗與結果分析

5.1 數據集在實驗中,采用基準問題生成器生成足夠多的訓練樣本集,作為卷積神經網絡的輸入數據.HFEBG基準問題生成器的輸入包含：

1) 建立好的一組算法集合

S={A1,A2,…,A};

2) 可調基準問題生成器;

3) 優化問題實例的算法.

輸出：與目標算法所對應的最佳問題實例.

SA={ABC,CoDE,CMA-ES}.

將集合中的算法依次設置為目標算法.選用最大集合高斯景觀生成器(MSG)作為問題生成器.選擇差分算法(DE)進化最佳問題實例,具體參數設置參照文獻[37].最后設置問題維數d0=10,局部最優值個數n0=10和重復迭代次數r=20,并且所有問題實例的搜索范圍在[-1,1]d0,最大評估數為d0×n0×103次.

通過以上參數設置運行程序后,分別產生了3類最佳的問題實例集,其中包含UE-ABC、UE-CoDE和UE-CMA-ES問題實例集,并為這3類問題進行標注標簽.詳細標簽值與問題的對應見表2.

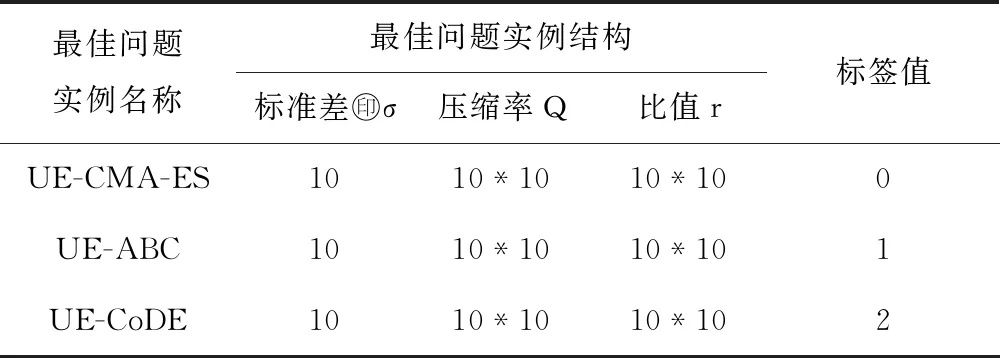
表2 問題實例結構和問題實例標簽值

5.2 實驗設置本實驗環境配置如表3所示.

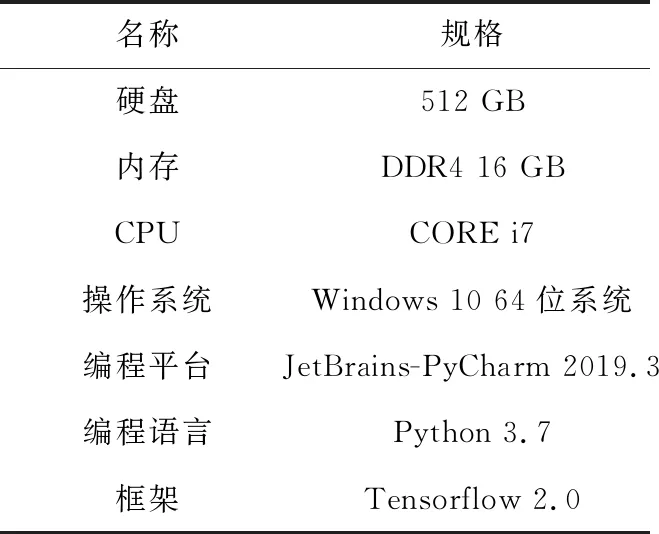
表3 實驗環境配置

實驗1中,將訓練迭代次數(epoch)設置為150,其中一輪迭代表示整個網絡訓練數據一次.將批量(batch size)設置為16,即每次訓練的實例數.使用Adam優化器來優化神經網絡,并將學習速率設置為3E-4.Adam優化器的第一動量(β1)、第二動量(β2)和ε分別設置為0.9、0.999和10E-8,遵循Tensorflow 2.0框架庫中的推薦設置.在每個時期結束時,使用驗證實例來測試網絡的性能.其參數在驗證實例上表現最好(即具有最高精度)的網絡將被保存.在訓練之后,使用測試實例來評估訓練有素的網絡的性能,并通過HFEBG共產生25 455個問題實例,讓其在3個優化算法(人工蜂群、復合差分進化算法和協方差自適應調整進化策略)獨立運行,并選擇最佳算法作為標簽.樣本實例按照6∶2∶2進行劃分,60%的實例用于訓練,20%的實例用于測試集和20%的實例用于驗證集,各類實例詳細樣本個數見表4.在這個實驗中,只研究了在維度為10的(D=10)問題實例在3個優化算法上的性能，于是只有3種可能的預測輸出，因此本實驗的基線精度應為1/3≈33.33%.為了獲得可靠的結果,重復訓練和測試過程5次,并記錄預測的3類問題實例的平均準確率.

表4 樣本數據集

實驗2中,將本文的算法選擇問題卷積神經網絡模型與傳統的機器學習的分類算法進行比較.傳統機器學習的數據預處理操作和訓練參數與卷積神經網絡中的設置相同,將算法選擇問題模型分別替換為：貝葉斯(Bayes)、邏輯回歸(Logistic Regression)、支持向量機(SVM).為保證實驗結果切實可信,重復執行5次操作.

5.3 分類指標依照常見的分類指標對算法選擇模型進行比較,其中包含精準率(Precision)、召回率(Recall)、F1分數值(F1-score)、準確率(Accuracy)和混淆矩陣等指標.在計算以上指標時,會使用到參數TP、FP、TN、FN.TP表示樣本真實類別為正值,預測樣本類別也為正值;FP表示預測類別為正值,真實類別為負值;FN表示預測類別為負值,但是真實類別為正值;TN預測類別為負值,真實類別為負值.

準確率是預測正確的樣本數量占總樣本量的百分比,計算公式為

Accuracy

(6)

精準率是模型預測為正樣本時結果中真實正樣本所占的百分比,計算公式為

Precision

(7)

召回率與精準率不同,是在實際為正樣本中被預測為正樣本所占的百分比,計算公式為

Recall

(8)

F

(9)

另外,還采可以用混淆矩陣,對分類模型進行評估.

5.4 實驗結果表5記錄了預測3類問題準確率結果.平均準確率為90.01%,完全優于基線準確率.對于大多數問題類,準確率都在90%以上.圖5記錄了算法選擇模型混淆矩陣結果.從圖5中可以觀察到,該模型能夠正確預測較多的第0類問題,是能夠幫助絕大部分的UE-CMA-ES問題實例準確找到最佳算法協方差自適應調整進化策略(CMA-ES).另外,相較于第0類問題，該模型將第1類和第2類問題錯誤分類的數量較多,但是也能為大部分的UE-ABC和UE-CoDE問題實體推薦最佳算法人工蜂群那和復雜差分.造成這兩類問題數據的錯誤分類,最有可能的原因是第1類和第2問題的相似特征比較多,所以導致了該結果.從表5和圖5的結果可以看出，該方法能夠為大多數優化問題實例推薦最合適的優化算法.

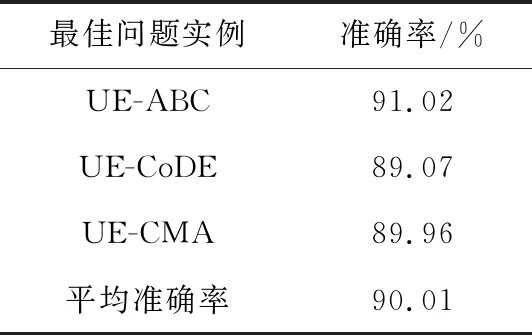
表5 預測實例準確率

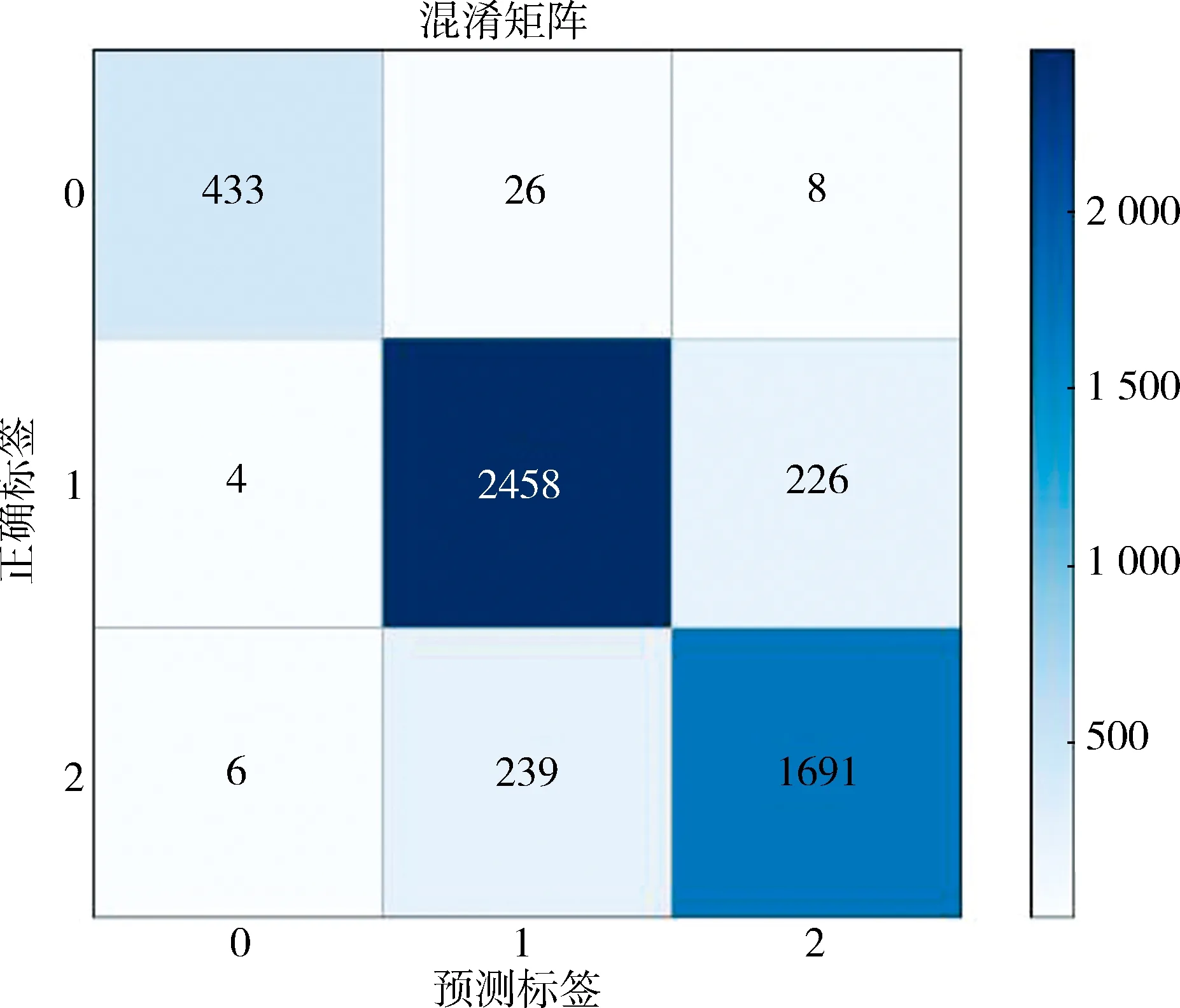
圖5 算法選擇問題模型混淆矩陣

在表6中,算法選擇問題模型的準確率可以達到90.01%,而貝葉斯的準確率僅僅只有54.51%,邏輯回歸和支持向量機中最高的準確率也只達到81.33%.很顯然這樣的結果是完全小于CNN的結果.另外,在精準率、召回率、F1分數值分類指標下CNN模型優于貝葉斯、邏輯回歸、支持向量機分類方法.該結果證明,在本文數據集上采用分類模型比傳統的機器學習方法更適合解決算法選擇問題.其原因在于淺層模型特征學習能力有限,學習到的特征不具備較好的分類特性.另外,從該實驗結果中還可以得出,無論是傳統的機器學習分類算法還是本文提出的基于深度學習的卷積神經網絡分類模型的結果都是遠遠高于這3類算法的試驗基線精度,這些方法都能夠有效的解決算法選擇問題,只是每種算法針對的這3類問題達到的準確率結果不同.

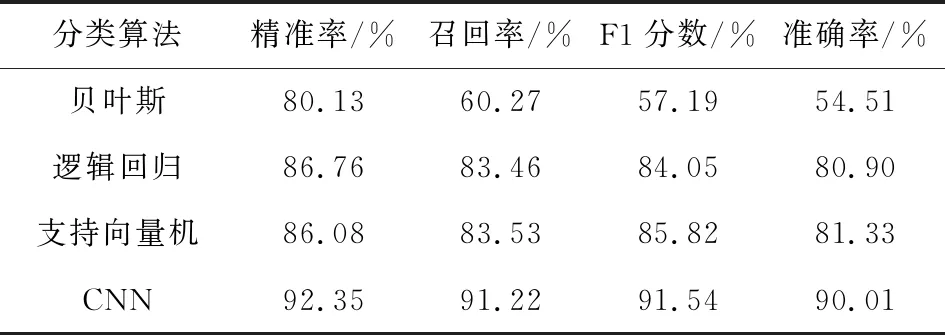
表6 分類模型算法性能比較

從以上實驗結果得出,本文提出的方法可以為大多數優化問題實例推薦最合適的優化算法.

6 結束語

算法選擇問題是一個重要的課題,因為不同類型的優化問題需要不同的優化算法.近年來,研究人員將算法選擇視為分類或回歸任務,并提出了許多解決方法.另外,神經網絡特別是卷積神經網絡在處理分類和回歸任務方面表現出很強的能力.然而,將深度學習應用于算法選擇的研究還比較少,而將深度學習應用于無約束的連續優化問題的算法選擇的研究就更少.

本文提出了基于深度學習的算法選擇模型,并利用卷積神經網絡結構對算法選擇的方法進行驗證.實驗利用訓練有素的卷積神經網絡來推薦優化算法,并采用預測的算法來優化給定的問題.比較實驗結果表明,深度學習方法中的卷積神經網絡可以有效地解決優化問題.

對于下一步的工作，首先,本文只是把算法選擇問題當作分類任務,其實將其作為回歸任務也是可行的.其次,本文的卷積神經網絡結構也可以替換成深度學習算法中更新的架構，這也是合理的.此外,還需要提高提取有效數據集的問題特征,查找能夠反映問題難度的問題特征,能夠更進一步探討算法性能與問題特征的關系.最后,不僅僅要關注低維問題特征,還應該從高維度問題對算法性能進行評估.