活用“兩差”辨“穩定”
文/李海寧

“兩差”即極差、方差,它們以不同的方式刻畫一組數據的離散程度。極差可以反映一組數據的變化范圍,方差則能反映一組數據偏離平均值的程度。這“兩差”都展現了數據之間的差異,描繪了數據的波動情況,即數據的離散程度。它們是初中統計學知識的重要內容,廣泛應用于生活。
一、極差的應用
例1某市5月25日—5月29日的氣溫情況如下:

請對該市這5天的日溫差情況進行分析。
解:5月25日的溫差是23-21=2(℃),5月26日的溫差是25-22=3(℃),5月27日的溫差是23-15=8(℃),5月28日的溫差是25-15=10(℃),5月29日的溫差是24-17=7(℃)。所以這5天的日溫差先逐漸增大再減小,相對來說5月25日與5月26日的氣溫較穩定。
【點評】計算日溫差是一個典型的極差應用的例子。因為極差只是利用了一組數據中的最大值和最小值,不能反映數據整體的離散程度,所以提供的只是數據粗略的離散情況。
二、方差的應用
例2為考察甲、乙兩種小麥長勢,農技人員在同一時期分別從兩塊試驗田中隨機抽取6棵麥苗植株,并標號為1~6,將測得的苗高數據繪制成統計圖。請你根據統計圖所提供的數據,計算甲、乙兩種麥苗高度的平均數和方差,并比較這兩種麥苗的長勢。
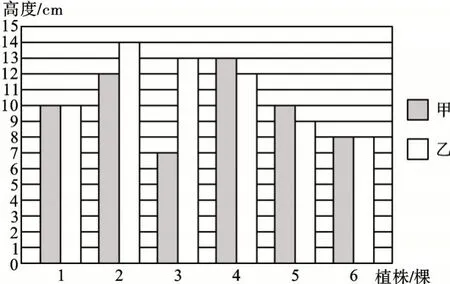

【點評】比較兩種麥苗的長勢不能僅考量數據的極端值,還應該關聯每一個數據,更精確地考量這組數據的離散程度(波動情況)。
三、“兩差”的綜合應用
例3甲、乙兩人在相同的情況下各打靶10次,打靶成績(單位:環)如圖所示:

(1)填表:
甲乙極差(環) 平均數(環) 方差(環2)
(2)從不同的角度評價甲、乙兩人打靶的成績。
解:(1)
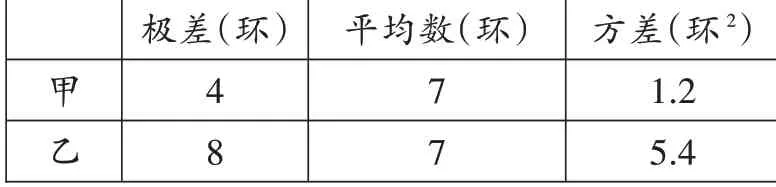
甲乙極差(環)4 8平均數(環)7 7方差(環2)1.2 5.4
(2)本題答案不唯一,下列解法供參考。
例如:
①甲、乙打靶的成績的平均數都是7環,說明兩人的打靶實力相當。
②甲、乙兩人打靶的成績的極差分別是4環和8環,說明甲打靶成績的波動范圍較小;甲、乙兩人打靶的成績的方差分別是1.2環2和5.4環2,說明甲打靶的成績更穩定。
③甲、乙命中9環及9環以上的次數分別是1次和3次,說明乙命中9環及9環以上的次數更多,更有潛力。
【點評】在實際問題中,極差與方差都是表示一組數據離散程度的統計量,都能反映數據的穩定性。但兩者還是有區別的,極差只是反映出一組數據大致的波動范圍,而方差關聯每個數據,能更精確地反映問題。我們在面對具體問題時要靈活選用。

