多因素綜合作用下高寒地區輸油管道剩余壽命的預測

張 維

（湖南鐵道職業技術學院，湖南 株洲 412000）

原油中含有大量的 CO2、H2S、SO2、酸堿鹽、固體沉淀物等，它們具有極強的腐蝕性，能引起管道內壁的電化學腐蝕和化學腐蝕，造成管道內壁的點蝕和坑蝕，嚴重時會使管壁變薄、產生裂紋，從而造成管道損壞失效[1]。高寒地區因地形和環境特殊，如若發生管道腐蝕開裂較難及時發現。因此，為保證管道的正常運行，必須對含有內腐蝕的高寒地區輸油管道進行剩余壽命的預測和估算。

在高寒地區，對含有內腐蝕缺陷的輸油管道進行剩余強度評估和剩余壽命預測可以防止由于管道腐蝕而引起的爆管事故，可以防止由于管道打壓試驗而引起的停工停產，也能防止由于過早更換管道而產生的巨大成本。早在20世紀70年代初期，美國、英國等發達國家就對管道腐蝕剩余強度評價進行了研究工作，頒布了如ASME B31G，CSA-Z184-M86[2]等與管道腐蝕剩余強度評價相關的標準與規范。利用上述標準與方法可以對含體積型腐蝕缺陷管體的完整性進行半經驗定量地分析，能夠對其剩余承壓強度進行預測，對其是否可以繼續安全地使用或采取降壓措施做出相應的判斷。由于有限元方法能較好的反映實際工況，因此，在我國，目前已有許多人將有限元分析方法用于管道剩余強度的計算，但這些研究大都針對的是單一因素，而實際上，管道缺陷處的等效應力往往是由多因素共同影響作用的。

文章將結合高寒地區管道的施工和敷設環境，利用 ANSYS有限元仿真軟件對含有內腐蝕缺陷輸油管道進行分析，建立含有內腐蝕缺陷的高寒地區管道模型，分析多因素在管道缺陷處的綜合影響，計算管道的失效壓力，結合理論壽命預測公式對管道的剩余壽命進行計算。

1 物理模型

在高寒地區，管線敷設分為地下敷設、地面敷設和支架敷設三種。沿線敷設時，約有一半長度采用的時地下敷設，這部分管段附近的土壤溫度變化不大；而另一半采用地上支架敷設，這部分管道的周圍氣溫變化范圍最大可達到66 ℃[3]。因此，管道本身和管基將在產生差異性熱應力，管道自身的重量、管道周圍土壤的應力、管道內流體運行的壓力和集中約束等也會對管道造成一定的載荷作用[4]。

目前，在高寒地區，一般選用尺寸為1 220 mm×14.3 mm 的管材，管材采用API 5LX標準中的高強度、耐低溫的X70鋼，其性能數據見表1。

表1 管道性能數據

文章所選用的仿真流體是原油，在仿真過程中綜合考慮了原油的物理性質，如密度、黏度等。已知原油的標準密度ρ20（即原油的密度在 20 ℃下是849.24 kg·m-3），則溫度為t時的原油密度，可以利用公式（1）來求得：

式中:ρt—溫度為t時的原油密度，g·cm-3；

ρ20—溫度為 20 ℃時原油密度，g·cm-3；

γ—原油密度的溫度系數，其值取 0.000 61。

運動黏度可由公式（2）計算：

式中：v—運動黏度，m2·s-1；

T—溫度，℃；

u—黏溫指數，1/℃，取值范圍0.01~0.03。

文章數據以阿拉加斯高寒地區的管道為基準。采用3.1 m·s-1的流速輸油，全程密閉輸送不加熱，利用管道內部流體沿程摩擦所產生的熱量，使沿線的油品溫度維持在 60 ℃左右[5]。通過式（1）（2）計算可得到在60 ℃時原油：密度為849.216 kg·m-3，運動黏度為7.068×10-5m2·s-1，動力黏度為6.002×10-2kg·(m·s)-1。

在管道仿真材料設置時，由于考慮到材料的非線性變化，采用了一種雙線性彈塑性模型，因此需要對管材的屈服強度和正切模量參數（Tangent modulus）進行設置[6]。文章選用的X70鋼材其切線模量為 934 MPa。

2 管道剩余強度分析

含內腐蝕管道的剩余強度分析是指在正常的工作壓力下，具有內腐蝕缺陷的管道是否能夠在滿足管道安全可靠要求的前提下繼續運行。但由于管道周邊環境、輸送介質的流速、管內的壓力以及腐蝕區域的尺寸大小等因素，都會影響到管道缺陷處的局部應力，當管道在各種載荷作用下時會在缺陷處出現應力集中，當產生的應力超出了管道的極限強度時，就會出現穿孔、破裂等現象，使管道無法正常運行下去。對含有內腐蝕缺陷的輸油管道進行剩余強度的分析，它既能夠對腐蝕導致的泄漏、裂管、爆裂等事故的產生一定的預警作用，同時也可以盡量減少由于頻繁更換管道而帶來的經濟浪費。一般選用的方法有以下兩種。

1）AMSE B31G標準方法

失效壓力[7]的計算公式為：

式中:Pf—管道剩余強度，MPa；

D—管道外徑，mm；

t—管道壁厚，mm；

d—腐蝕缺陷深度，mm；

l—腐蝕缺陷長度，mm；

M—膨脹系數；

2）有限元分析法

隨著 ANSYS有限元分析方法在工程上的廣泛應用，許多學者都開始采用這種非線性有限元方法來研究管道缺陷之間的相互作用對管道剩余強度的影響[8]。這種方法不僅可以模擬管道內復雜的腐蝕狀態，又能同時考慮各種載荷的耦合作用，使模型更加接近實際，從而提高了模擬結果的準確性。在選用有限元方法分析時，材料失效準則、有限元模型假設、模型參數等都會對結果的準確性產生直接影響。

文章選用的是 ANSYS有限元分析法來對含有內腐蝕缺陷輸油管道的剩余強度進行分析。

2.1 仿真模型的建立

文章在應用 ANSYS有限元方法對管道進行受力分析前，假定：①建模時考慮流體內壓對管道內壁的作用以及兩端的固定約束作用；②在高寒地區，考慮環境溫度的影響；③埋地管道周圍管土的相互作用較為復雜[9]，但與其他因素相比其影響較小，因此，建模時不考慮周圍土壤對管外壁的作用；④管道的腐蝕缺陷只對缺陷附近的管道應力產生影響，所有僅分析具有內腐蝕缺陷的管段。基于上述假設及前提，建立了以下仿真模型。

2.1.1 仿真模型的基本信息

1）管道基本信息。選取仿真計算管道的長度為20 m，管道壁厚0.014 3 m，管徑1.22 m，保溫層厚度0.1 m。根據ASME B31G—2009來確定內腐蝕的尺寸：缺陷的最大許可深度可設為公稱壁厚的80%。如缺陷深度未達到公稱壁厚的10%，此時可不用考慮缺陷的存在[10]。

2）邊界條件的設置。對管道內部進行填充，并命名為Fluid，將原有的Solid重命名為Pipe，保溫層命名為 Wall。流體域入口設置為 inlet，出口為outlet。

圖1 管道仿真模型

2.1.2 網格劃分

1）內部流體的網格劃分：對流體進行網格劃分時要對管壁和保溫層進行抑制，同時，還應注意對內腐蝕處的網格進行加密。

2）管道和保溫層的網格劃分：劃分管壁和保溫層的網格之前，應先對流體進行抑制，然后在 Model模塊下進行網格劃分。為了便于后期載荷的加載和結果的區分，在網格劃分完后，還需要對有關面進行命名。將保溫層的外壁面命名為Wall-outer。為了進行流體壓力數據傳輸，需選擇一個管道內壁面，將其命名為Pipe-Fluid。管道兩端端面則分別命名為Pipe-in和 Pipe-out，保溫層兩端的端面分別命名為Wall-in 和 Wall-out。

2.1.3 邊界條件的加載

文章案例采用熱流固耦合方法進行模擬計算，一共要用到 Fluent、Steady-State Thermal和 Static Structure三個模塊來完成流場、流體溫度場、固體溫度場和固體熱應力的計算，這三個模塊之間通過數據傳輸線相連。

邊界條件的設置主要包含了內部流體和外部固體的邊界條件加載。進行內部流體邊界條件設置時，入口選擇速度入口，也就是 Velocity-inlet，出口選擇壓力出口，即Pressure-outlet。

2.2 失效準則

文章選用 ANSYS軟件后處理中的等效應力（Von Mises）模塊，來對管道腐蝕區的最大等效應力進行分析。選用材料力學第四強度理論作為失效準則，也就是當管道腐蝕區的最大等效應力超過管道材料的屈服強度時，即認為該管道極大可能會失效[11]。在三維主應力空間上，Von Mises[12]條件表述為：

式中：σv—屈服應力，MPa；

σ1、σ2、σ3—分別為x、y、z方向上的主應力，MPa。

2.3 仿真結果分析

由圖2可知，腐蝕處的最大等效應力隨著環境溫度的降低逐漸減小。對比有保溫層管道與無保溫層管道最大等效應力可知保溫層在低溫條件下，對管道起到了一定的保護作用，并且保溫層越厚，對管道的保護作用越大。

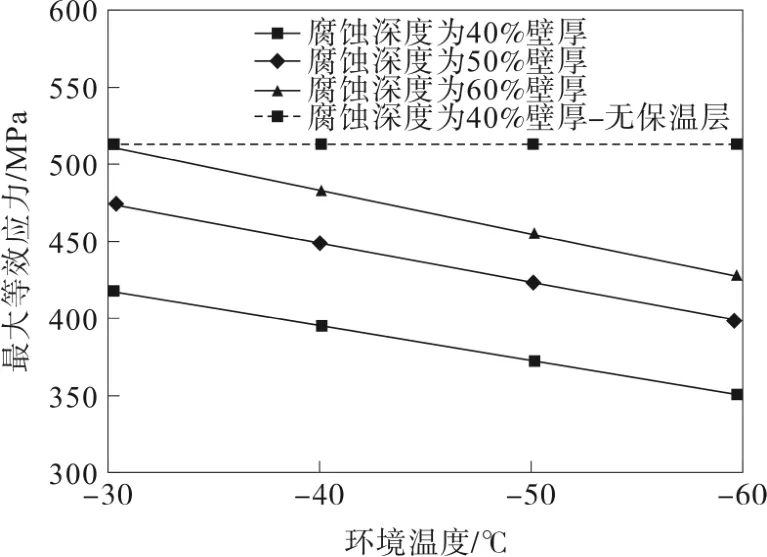
圖2 環境溫度和最大等效應力的關系

由圖3可知，當流體流速的變化時，管道的最大等效應力幾乎沒有改變。這主要是由于仿真分析時，流體對象為純流體，在湍流狀態下，其流場的速度分布變化很小。然而，這并不能否認流體的流速在化學腐蝕過程中的重要作用。因為原油中含有顆粒雜質，顆粒本身會對管道造成一定的沖擊，不同的流速會影響到顆粒的運動，也會影響到原油中腐蝕成分之間的分布，導致腐蝕速度快慢不一，從而最終使管道的剩余使用壽命受到影響。

圖3 流速與最大等效應力的關系

由圖4可知，腐蝕區最大等效應力隨管道內部壓力的增大而增大。且腐蝕深度越大，內壓的作用更為明顯，這說明由管道流體運行產生的內壓對腐蝕區的應力作用是不容忽視的。

圖4 內壓和最大等效應力的關系

不同的腐蝕尺寸參數對管道的最大應力數值與分布有不同的影響。從圖5可看出，管道腐蝕區的最大應力隨著腐蝕深度的加深而呈線性增加，其影響效果是顯著的。

圖5 腐蝕深度和最大等效應力的關系

從圖6可看出，當腐蝕坑的軸向長度增加時，管道腐蝕區的最大等效應力值也隨之增加，但相對腐蝕深度的變化而言，其變化幅度較小；當腐蝕坑的徑向長度增加時，腐蝕區最大等效應力幾乎沒有變化。

圖6 軸向長度/徑向長度和最大等效應力的關系

綜上所述，在保持腐蝕區參數不變時，腐蝕區最大等效應力隨管道內壓的增加而呈上升趨勢；不隨流體的流速發生改變；隨環境溫度的降低而下降。在保持其他參數不變時，對腐蝕區最大等效應力的影響效果依次為：腐蝕深度＞軸向長度＞徑向長度，同時仿真結果顯示，該模型的最大等效應力值不會隨著參數的改變而線性地發生變化，這說明了理論計算公式地應用范圍是有限地，也凸顯了有限元仿真方法的優勢。

3 管道剩余壽命的預測

剩余壽命預測對于管道安全狀況的衡量和維修策略的制定具有十分重要的意義。根據上述仿真分析結果可以看出，腐蝕深度是影響管道失效的最關鍵因素，故可通過有限元分析法來計算在不同腐蝕深度下的管道失效壓力。即逐步增大腐蝕深度的尺寸，當管道腐蝕區所受的最大等效應力值大于485 MPa（管道的屈服強度）時，此時的腐蝕深度尺寸為管道允許的最大腐蝕深度。分析結果如圖7所示：當最大等效應力接近于屈服強度時，腐蝕深度約為9 mm。

圖7 腐蝕坑直徑與最大等效應力的關系

得到極限腐蝕深度時管道失效壓力的步驟為：①將根據ASME B31G計算出的安全工作壓力值作為仿真分析時的初始工作內壓。②將初始工作壓力下所分析得到的最大等效應力值與管道的屈服強度進行比較。③當仿真分析得到的腐蝕區最大等效應力值比屈服強度大時，則用現階段仿真的壓力值減去相應的差值作為下一步仿真的初始壓力；反之，當仿真分析得到的腐蝕區最大等效應力值比屈服強度小時，則用現階段仿真的壓力值加上相應的差值作為下一步仿真的初始壓力，來實現初始工作壓力的調整。④反復調整工作壓力值，直到分析得到腐蝕區最大等效應力值與屈服強度之差在5%之內時，可認為，此時對應的壓力值就是該工況下管道所能承受的最大內壓，即管道的失效壓力值。根據以上步驟，采用有限元方法分析得到，當管道腐蝕缺陷深度為9 mm時，管道的失效壓力為10 MPa。

圖8 失效壓力仿真計算流程

計算含內腐蝕管道的剩余使用壽命經驗[13]公式如下：

式中:tr—管道已使用年限，a；

k—校正系數，值取0.85[13]；

δs—管道臨界壁厚（達到屈服強度時的腐蝕壁厚），mm；

SM—安全余量，其值等于計算失效壓力與屈服壓力的比值減去最大操作壓力與屈服壓力的比值；

t—管道公稱壁厚，mm；

GR—腐蝕速率，mm·a-1；

ts—管道剩余壽命；

td—管道設計使用壽命。

管道的各項性能參數通過上述仿真分析已知，在腐蝕速率為0.048 mm·a-1，腐蝕厚度9 mm時，通過式（6）計算出管道的已使用年限為36.76年。在已知管道設計使用壽命時，通過式（7）就能夠快速得到管道在任意壁厚下所對應的剩余使用壽命。

4 結 論

1）采用ANSYS-Workbench軟件對含有內腐蝕缺陷的高寒地區管道進行了建模，并對其腐蝕缺陷處所受的等效應力與各因素之間的關系進行了比較分析。結合剩余壽命預測經驗公式，對含有內腐蝕缺陷的高寒地區管道進行了剩余壽命估算，這對制定高寒地區管道的檢修和換管計劃提供了一定參考價值。

2）文章結合有限元分析法和經驗公式，完成了對管道剩余使用壽命的預測，但仿真分析的環境是純流體，而實際運行的原油管道中往往會存在顆粒等雜質，這些雜質在流動過程中，會影響管道的內腐蝕速度。因此，若要實現更為精準的預測，還需進行大量的現場檢測和實驗數據。