大壩洪水漫頂風險率理論研究

張文燦

（深圳市廣匯源環境水務有限公司九江分公司,江西 九江 332000）

1 引言

我國是一個地勢特別復雜的國家,由于地勢復雜,導致我國常年遭遇到洪水的侵害,尤其是南方地區,大洪水直接損害我國人民群眾的生命安全和財產安全,雖然每個河流附近,都有大壩屹立在河流之上,但依然沒有辦法避免這些問題。基于此現象,針對大壩洪水漫頂風險率進行研究分析,這對我國大壩遇洪水漫頂現象產生時,具有重要指導意義。

鑒于此現象的嚴重性,我國大量學者對此進行大量的研究分析,也得出了相關理論依據。董華飛等[1]研究大壩洪水漫頂情況下涌浪疊加作用,由此進行模型實驗。陳生水等[2]利用混凝土面板上構造成分的破壞機理,提出一種數值計算方法,該方法可以有效模擬混凝土面板上構造成分的破壞過程。胡澤林等[3]提出LHS-MC 與Copula 函數算法公式,分析水電站在加固情況下的洪水漫壩率，并控制不同變量研究其變化對結果的影響。石振明等[4]通過研究壩體結構,分析大壩結構問題引起的事故,進而進行室內模型實驗、現場試驗和數值模擬研究潰決過程下,大壩水土物質移動規律。黃靈芝等[5]基于模糊數學理論,建立歷史失事數學模型,利用模糊數學中隸屬函數分析失事程度并進行分析。張修照等[6]介紹我國大壩在洪水漫頂時的潰壩過程,并提供資料分析其中原因。李清富等[7]根據洪水漫頂導致大壩潰壩的原因進行分析,對大壩洪水漫頂風險情況進行評估,并建立風險模型,探討不確定因素對洪水漫頂風險率的影響以及解決方法。張興凱等[8]建立物理模型演示尾礦庫的大壩在洪水漫頂情況下的潰壩過程。基于沖刷機理和模型相似理論,分析在洪水來臨時的防護措施。

由上述研究情況可知,雖然目前對于大壩洪水漫頂風險率研究得到多方學者探究,但沒有考慮洪峰、洪量相關關系,也未對比多種計算函數的結果,并進行對比。本文通過數值計算,研究大壩前端最高水位分布情況和系數大小對大壩洪水漫頂風險率的影響。

2 計算模型

2.1 工程概況

某大壩建設工程位于河流下游,且水流湍急,該地區位于我國南方,多雨,因此每有大雨降臨之時,便會產生洪水。大壩所處流域面積為14430 km2,選擇洪水時間超過7 天的過程。壩高為206 m,高度為151 m,長度為654 m。而大壩的隔河水位線高192.2 m,并且擁有5 億m3儲水庫容。利用公式計算,研究大壩在洪水來臨時的風險率。

2.2 模型建立

本試驗通過風險率理論公式進行計算,建立風險分析模型并對其洪水峰量進行分布處理和風險率計算。基于分析模型的建立,得出風險率的表達式為：

式中：L 為系統荷載；R 為其對應抵抗力。

L 和R 的情況可以反映出工程結構和實際存在的問題。對于分析模型,水庫最高水位為Hmax,其也表示大壩能夠承受的最大荷載,是抗力,由此得到計算公式：

式中：FHmax（hmax）為最高水位Hmax的概率分布情況函數。

由于在實際工況中,FHmax（hmax）難以被求出,由此通過蒙特卡羅模擬法對風險率進行求解。假設Q 和W 分別為洪峰和洪量,其分別對應小寫字母q 和w 表示,將Q 和W 進行聯合,形成一個二維分布函數：

式中：u 和ν 分別為邊緣分布情況；F（q,w）為Q,W 的聯合分布函數；為公式參數。

利用三種變量公式,分別為Gumbel-Hougaard、Frank 和Clayton,對公式進行依次1～3 的編號編輯,建立公式τ與值的關系表,如表1 所示。并由此計算出統計量Sn,公式如下所示：

表1 三種編號對應的公式與τ 值的關系表

基于洪水峰量的分布情況,對風險率進行計算,求解洪水漫頂風險率。通過Copula 函數得出洪水的過程線：

式中：DFH（t）和（TFH（t）分別為洪水過程和在t 時的洪水流量；QD、WD、w 和q 分別為洪峰流量、DT 時間內的洪量、洪峰流量和洪量。

重復Copula 函數計算n 次,可以得到Hmax值,并采用期望公式可得洪水漫頂風險率計算公式：

3 結果分析

3.1 分布情況的確定

根據某城市某項目大壩位置,選擇水庫洪峰和洪水時間超過7 天的洪水過程進行參數設計,具體情況見表2。

表2 水庫參數設計值

將表1 的計算公式與表2 的參數進行結合,建立洪峰和洪水時間超過7 天洪水量的聯合分布情況,并且基于Kendall算法計算參數,具體情況見表3。

表3 庫參數設計值

由表3 可知,P 值均大于0.05,表明設計都是合理的。由此對觀測變量的經驗分布情況和理論分布情況進行了對比,見圖1。

圖1 經驗分布情況與理論分布情況對比曲線

由圖1 可知,對比斜角為45°,表明兩種情況的一致性,證明經驗頻率與理論頻率的分布擬合情況很好,建立的分布模型也是合理的。

3.2 計算結果

基于對風險率計算過程,建立計算函數,根據條件分布隨機生成大量的洪峰和洪量,并對其進行組合,得出其相關結構。并且根據洪水時間超過7 天洪水量的過程,以經驗頻率為基礎,基于期望公式得出大壩前端的最高水位分布曲線見圖2。

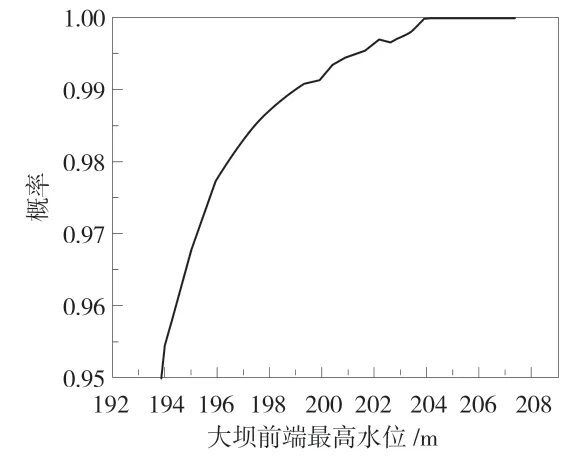
圖2 大壩前端的最高水位分布對比曲線

由圖2 可知,概率與大壩前端的最高水位曲線分布,在大壩最高水位為204 m 時,概率已經接近1,由此可以得出其風險率為379000。

3.3 取值的影響分析

三種函數對應的大壩前端最高水位分布曲線見圖3,其中編號1～3 分別為Gumbel-Hougaard、Frank 和Clayton 函數公式。

圖3 三種函數公式對應的大壩前端最高水位分布曲線

由圖3 可知,三種概率公式都在大壩前端最高水位204 m 時,概率達到1,其中編號3 算法的概率幅度最大。當大壩前端最高水位為195 m 左右時,編號2 算法的概率幅度超過編號1 算法概率幅度,但當大壩前端最高水位198 m 左右時,編號1 算法和編號2 算法的概率幅度極為接近,并且曲線保持一致的角度。可以肯定編號1 算法和編號3 算法低估洪水風險,編號2 算法高估洪水風險,因此不同編號算法的風險率具有很大差異程度,所以在選擇算法時需要仔細斟酌。

3.4 系數大小影響分析

系數大小與大壩前端最高水位概率分布情況情況見圖4。

圖4 不同系數與大壩前端最高水位概率分布曲線

由圖4 可知,隨著系數增大,概率隨之變小,但當大壩前端最高水位升高時,最終概率都會回到1,其變化曲線幅度會隨著系數大小變大而變緩。為進一步研究系數與風險率關系,建立與之對應的洪水漫頂風險率與系數關系曲線,見圖5。

圖5 不同系數與洪水漫頂風險率關系曲線

由圖5 可知,隨著系數的增加,大壩洪水漫頂風險率也隨之增加,并且相關系數為0、0.5 和1 所對應的大壩洪水漫頂風險率分別為0、2.9 和 7.2,由此可知,在相關前提條件下,是被高估了,但在不相關情況下則是被低估了。

通過系數大小對漫頂風險率概率分析可知,Copula 函數計算方法合理有效,其能夠準確得到洪峰、洪量的相關關系,使公式計算得到大壩洪水漫頂風險率更貼近事實。

4 結論

（1）理論分布情況和經驗分布情況對比,表明兩種情況一致性,證明經驗頻率與理論頻率分布擬合情況很好,建立分布模型也是合理的。

（2）大壩前端最高水位為204 m 時,概率已經接近1,由此可以得出其風險率為379000。

（3）三種概率公式都在大壩前端最高水位204 m 時,概率達到1,編號3 算法概率幅度最大。當大壩前端最高水位195 m 左右時,編號2 算法超過編號1 算法概率幅度,但當大壩前端最高水位198 m 左右時,編號1 算法和編號2 算法的概率幅度極為接近,并且曲線保持一致的角度。但編號1 算法和編號3 算法低估洪水風險,編號2 算法高估洪水風險,并且不同編號算法風險率差異程度很大。

（4）隨著系數的增加,大壩洪水漫頂風險率也隨之增加,并且在相關前提條件下,大壩洪水漫頂風險率被高估了,但在不相關情況下則是被低估了。從而得知Copula 函數計算方法合理有效,其能夠準確得到相關系數,更加貼近實際應用。