基于模型預測控制的諧振式無線電能傳輸系統

王曉蘭，石圣昀，王惠中

（1.蘭州理工大學電氣工程與信息工程學院，甘肅 蘭州 730050；2.甘肅工業過程先進控制重點實驗室，甘肅 蘭州 730050）

近年來，磁耦合諧振式無線電能傳輸技術(Magnetically Coupled Resonant Wireless Power Transmission,MCR-WPT)憑借其安全、便捷、傳輸距離適中的優點，在電子設備、醫療設備、航空等領域得到大量應用[1]，但由于系統在實際運行中沒有足夠的穩定性[2]，整個系統缺乏可靠性和靈活性，因此提升系統輸出電壓的可控性以及對設定值的跟蹤能力非常重要[3]。

由于雙LCL 型拓撲結構具有較好的適應性、可操控性[4-5]，因此選擇雙LCL 作為MCR-WPT 系統的拓撲結構。目前適用于MCR-WPT 系統的建模方法較多，文獻[4]利用離散迭代建模法建立系統模型；文獻[5]基于遺傳算法搜尋最優控制參數，建立模型，實現對系統的控制；文獻[6]使用能量流理論建立模型；文獻[7]針對SS 拓撲結構，利用擴展函數法進行建模。對于系統的控制器，文獻[8]使用閉環數字PI控制器進行控制；文獻[9]提出一種基于最大接收電壓的頻率跟蹤控制方法；文獻[10]設計了一種積分滑膜控制器。

傳統控制方式存在超調量較大，調節時間長[11]，無法快速、準確地跟蹤設定值的問題，文中設計選擇具有響應迅速、調節時間短優點的模型預測控制器來調節輸出電壓，并加入PID 控制器、模糊PID 控制器進行對比。

1 雙LCL型MCR-WPT系統建模

1.1 雙LCL型系統工作原理

圖1 為采用雙LCL 拓撲結構的MCR-WPT 系統電路結構圖。

圖1 雙LCL型MCR-WPT系統電路結構圖

在該系統中，直流電源Udc作為輸入，經過逆變網絡，將直流電轉變為交流電，此時逆變器輸出電壓Uin，經過諧振電感L1、諧振電容C1、電感線圈Lp，通過磁感應耦合從原邊線圈Lp傳遞到副邊線圈Ls，副邊補償網絡產生諧振，由整流網絡D1-D4和濾波電容Cf將交流電轉換為直流電對負載RL輸出。

在傳輸過程中，為使系統工作在諧振頻率的電壓穩定，需要滿足L1=Lp、L2=Ls且諧振頻率ω=，原邊發射線圈電流I1、輸出電流Io計算如下：

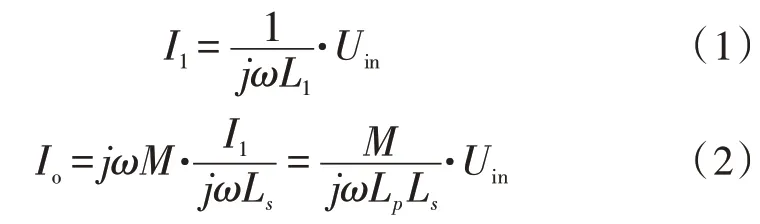
進一步得到：

其中，A=為常數，故由式（3）可知，系統輸出Uout只與輸入Uin有關，確定了系統參數間關系，證明通過控制器調節輸入電壓使系統輸出電壓穩定并達到設定值可行。

1.2 電路建模

廣義狀態空間平均法(Generalized State Space Averaging,GSSA)用函數來表示電路中非線性環節的開關規律，通過等效電路得到拓撲結構的微分方程，對狀態變量進行傅里葉級數展開并分離實部虛部，得到系統狀態空間方程。通過此方法建立解決MCR-WPT 系統復雜、高階、非線性問題的模型[12]。

雙LCL 拓撲結構等效電路如圖2 所示。

圖2 雙LCL拓撲結構等效電路

圖2 中，g1(t)、g2(t)分別為描述逆變器、整流模塊開關規律的函數，邏輯值為1 和-1。根據圖2 所示的等效電路，利用基爾霍夫定律可得到系統微分方程，并進行傅里葉級數展開，將方程中直流分量用0 階表示，交流分量用1 階表示[13]，得到廣義微分方程，展開并分離方程中各狀態變量系數的實部和虛部，得到廣義狀態變量如下：

最終得到系統廣義狀態空間模型如下：

式（5）中，A∈R13×13，B∈R13×1，C∈R1×13，D=[0]，y為輸出變量。

2 模型預測控制器

2.1 模型預測控制原理

模型預測控制(Model Predictive Control,MPC)是解決在每次采樣有限時間內最優問題的一種控制方法，相比傳統PID 控制，具有響應速度快、調節時間短、震蕩少的特點。MPC 原理如圖3 所示。

在圖3 中，曲線1 為參考軌跡，利用當前時刻k的測量值和模型，預測系統未來時間的輸出，即曲線2。圖中矩形波4 為通過求解目標函數的最優問題而得到的預測控制量，用該控制量的第一個值作為實際控制量，再次預測系統未來時間的輸出，并持續重復完成對系統的滾動優化，實現對輸出的持續控制。

圖3 MPC原理圖

2.2 預測方程

MPC 是對模型未來動態的預測，為了使式（5）中的模型適用于MPC 控制器，需要將該模型寫為離散化形式[14]，如式（6）所示:

式中，k為當前時刻，x(k)為測量值，Δx(k)為預測系統未來狀態的起點，y(k)為系統輸出，由此經過推導可進一步得到系統輸出在未來p步的預測方程：

Yp(k+1|k)為系統p步的輸出矩陣，ΔU(k)為p步控制輸入變量矩陣，其中：

2.3 滾動優化

滾動優化是通過使式（9）最優準則的值為最小來確定的，使系統在未來的輸出值更加接近設定值。

因此，整個滾動優化過程就是將每個采樣時刻優化解的第一個值作用于系統，并反復進行，采用的是時間向前滾動式的優化策略。雖然沒有設立一個不變的全局目標，只能得到次優解而不是最優解，但是卻能解決系統模型在匹配、時變等情況下遇到的不確定性問題[15]。

2.4 反饋校正

在系統實際運行過程中，對于模型的預測不可能與實際完全一致，因此在控制過程中，比較實際輸出值與預測值，得出輸出誤差e，利用誤差對模型的預測值進行修正，進而對整個模型的預測值進行補償。綜合以上步驟可設計如圖4所示的MPC控制器。

圖4 雙LCL拓撲結構MCR-WPT系統MPC控制器

3 仿真實驗

基于以上模型，利用Matlab/Simulink 平臺驗證MPC 控制器的控制效果和跟蹤能力。MPC 預測水平Np=1 000，控制水平Nc=20，其余參數如表1 所示。仿真結果如圖5-8 所示。

表1 電路元件參數表

圖5 MPC控制器作用時系統輸出電壓波形圖

圖5為MPC控制器作用時系統輸出電壓波形圖，設定輸出電壓80 V，仿真時間0.2 s 時，系統輸出電壓在0.043 s達到最大值82.44 V，存在2.44 V 的偏差；系統輸出電壓在0.1 s時達到穩定值80.01 V，控制精度為99.9%，整個過程響應迅速，超調量小。圖6為仿真時間4 s時，MPC、PID、模糊PID三種控制器的控制效果，系統輸出電壓達到設定值并穩定分別需要0.71 s、2.84 s、3.14 s，MPC 控制器相較于PID、模糊PID 控制器，時間分別縮短了2.13 s、2.43 s，調節速度更快。PID 控制器精度為99.76%，模糊PID 控制器精度99.72%，MPC 控制器在精度上提高約0.2%，控制精度是指控制系統中最終的控制參數值與設定值的符合程度，即最終穩定值與設定目標值的比值[16]，超調量、對設定值的偏差也明顯更低，由此驗證了MPC 控制器處理MCR-WPT系統響應速度快、震蕩少、精確度高的優點。

圖6 MPC、PID、模糊PID控制器作用時系統輸出

圖7-8 為當設定參考值在40～80 V 范圍內每1.25 s 變動一次，三種控制器分別作用時的跟蹤能力對比圖。當電壓發生變動后，MPC 控制器在電壓上升時需要0.1 s 達到設定值，下降時需要0.09 s 達到設定值；PID 控制器電壓上升時需要1.25 s 達到設定值，下降時需要1.3 s；模糊PID 控制器電壓上升時需要1.25 s 達到設定值，電壓下降時需要1.30 s，MPC控制器響應速度在電壓上升時與PID 控制器、模糊PID 控制器相比分別提升1.15 s、1.2 s，下降時與PID控制器、模糊PID 控制器相比均提升1.21 s 且超調量均明顯小于其他。MPC 控制器在電壓再次變動前即可達到設定值，精確度99.9%，PID 控制器精度為99.76%，模糊PID 控制器精度為99.72%，高于PID、模糊PID 控制器，驗證了MPC 控制器對于設定值的跟蹤能力優于PID、模糊PID 控制器，對于MCRWPT 系統有更好的控制效果。

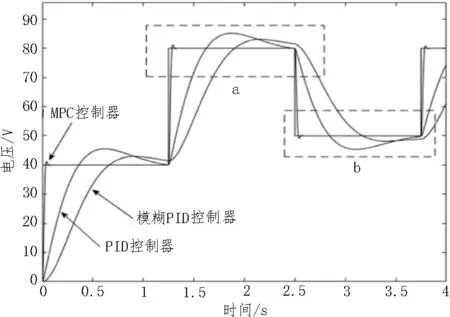
圖7 設定值變化時三種控制器的跟蹤效果

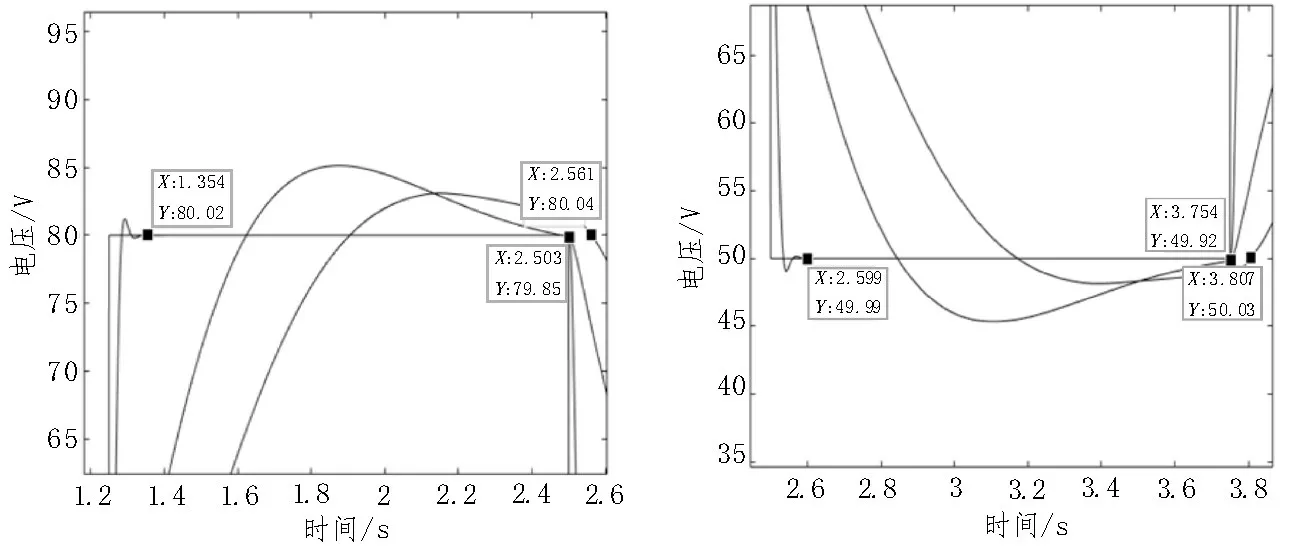
圖8 對圖7虛線框a、b局部放大

4 結論

利用MPC 控制器控制雙邊LCL 拓撲結構的廣義狀態空間模型輸出，解決了傳統控制器控制系統輸出電壓時存在超調較大、調節時間長、響應速度慢的問題。仿真結果表明，上述方法設計的MPC 控制器在相同環境下能夠準確快速地跟蹤設定電壓，在0.1 s 內達到設定值，精確度為99.9%，相比PID、模糊PID 控制器，其調節時間大幅縮短，輸出平滑且超調量小，具有更好的穩定性和控制精度，為MCR-WPT系統控制策略提供一種新的方式。