F=1旋量玻色-愛因斯坦凝聚的向列壓縮

楊超楠,鄭任菲，趙興東,周魯

(1.華東師范大學 物理與電子科學學院,上海 200241；2.合肥工業大學 物理學院，合肥 230009；3.河南師范大學 物理學院，河南 新鄉 453007)

與標量玻色-愛因斯坦凝聚[1-5](Bose-Einstein condensate,BEC)相比，旋量BEC是磁性超流，所以展現出更加豐富的物理性質，成為近幾年來實驗和理論的研究熱點[6-13].很多有趣的物理學現象在該體系中被觀測到，比如量子糾纏[7]、自旋壓縮[8]和自發退磁現象[14]等.因而，旋量BEC領域的研究具有極大的價值.自旋壓縮對量子信息的研究有重要的意義.在超高精密測量領域的作用也尤其突出.與自旋壓縮不同，向列壓縮引入了高階的向列張量，展現了更加豐富多元的壓縮性質[15].CHAPMAN等人[16]首次在實驗上實現了旋量BEC的向列壓縮.2013年，他們又發現了不穩定點與壓縮之間的關系[17].同年，日本東京的一個小組將向列壓縮歸類為第二類壓縮，并且給出了詳細的分類依據[18].很快，利用周期性微波脈沖將自旋向列壓縮存儲在旋量BEC中的方案出現.在適當的脈沖周期和相移條件下，壓縮可以增強并保持較長時間，從而實現最大壓縮的存儲[19].同時，腔場中的BEC也可以產生向列壓縮[20].

本文從旋量BEC的模型[21-23]出發，在理論上總結了自旋向列壓縮的產生和動力學演化行為[24]，在自旋向列球上展示了極化態為初態的自旋向列壓縮的物理特性和壓縮圖像.然而，僅僅描繪極化態的壓縮行為顯然是不充分的，缺乏普遍性，因此，還研究了在任意初始態下系統的向列壓縮行為.

1 旋量BEC模型的介紹

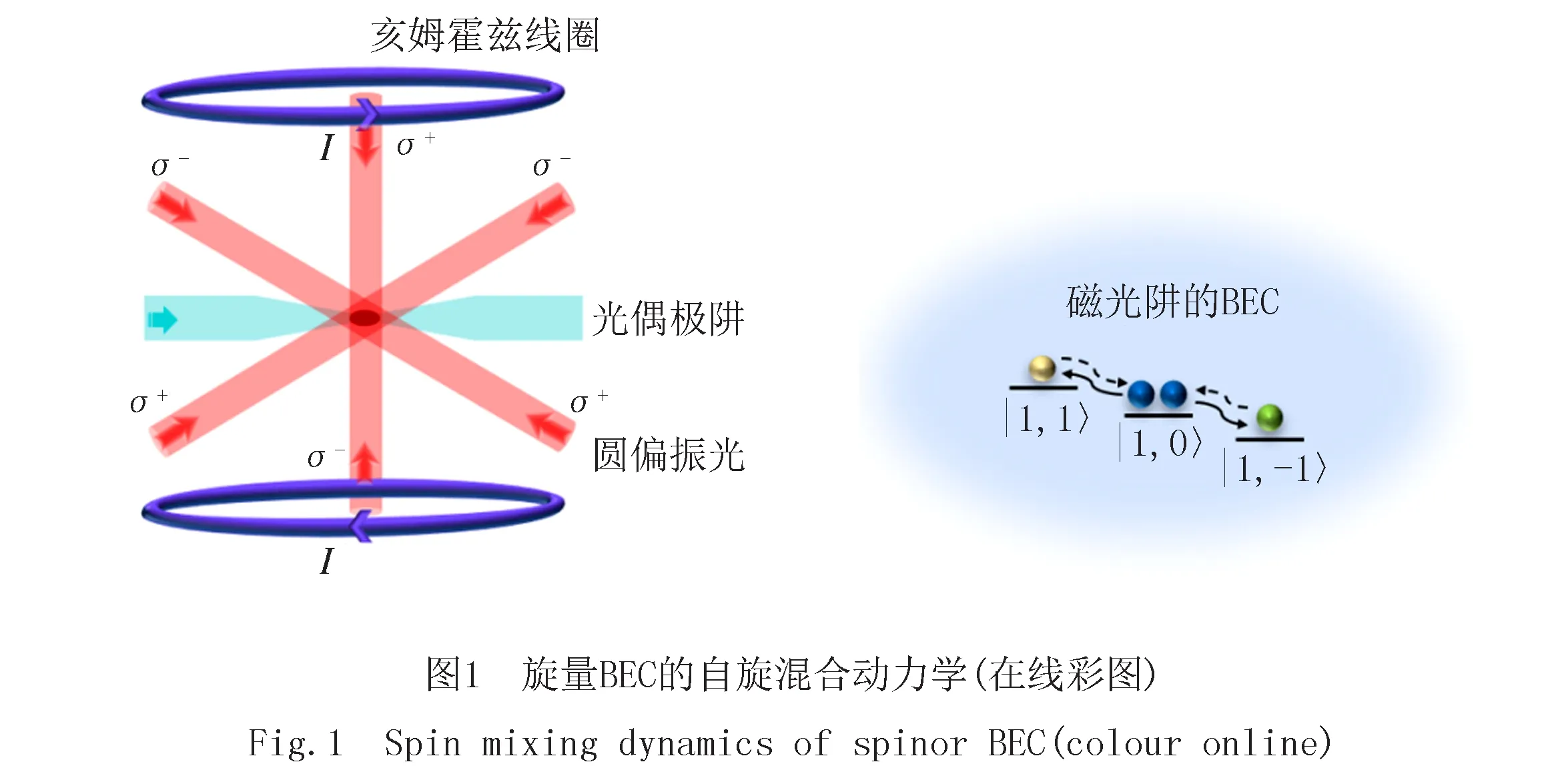
考慮被冷卻并囚禁于三維磁光阱中的超冷原子，用于產生旋量BEC.對于F=1的旋量BEC，自旋磁量子數mF是-1,0,1,對應的3種塞曼態|F,mF〉：|1,1〉,|1,0〉|1,-1〉，如圖1所示[25-26].根據單模近似原理，在有限的磁場中旋量BEC的哈密頓量[27-28]

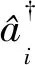
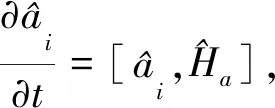
(1)

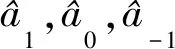
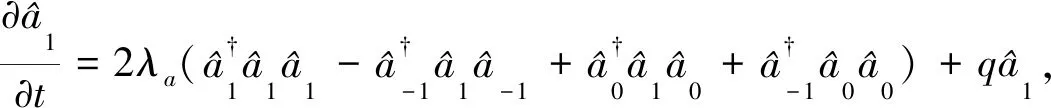
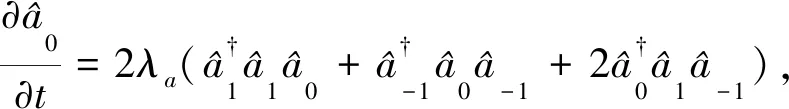
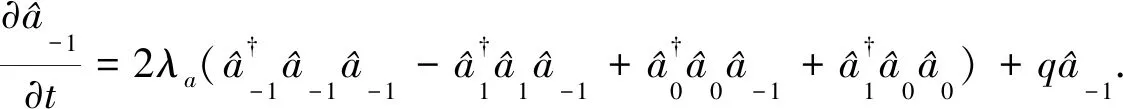
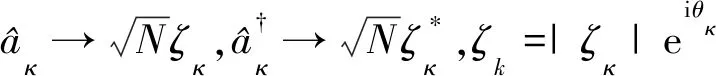
(2)

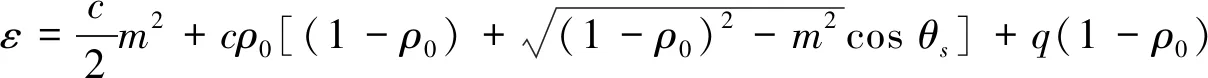
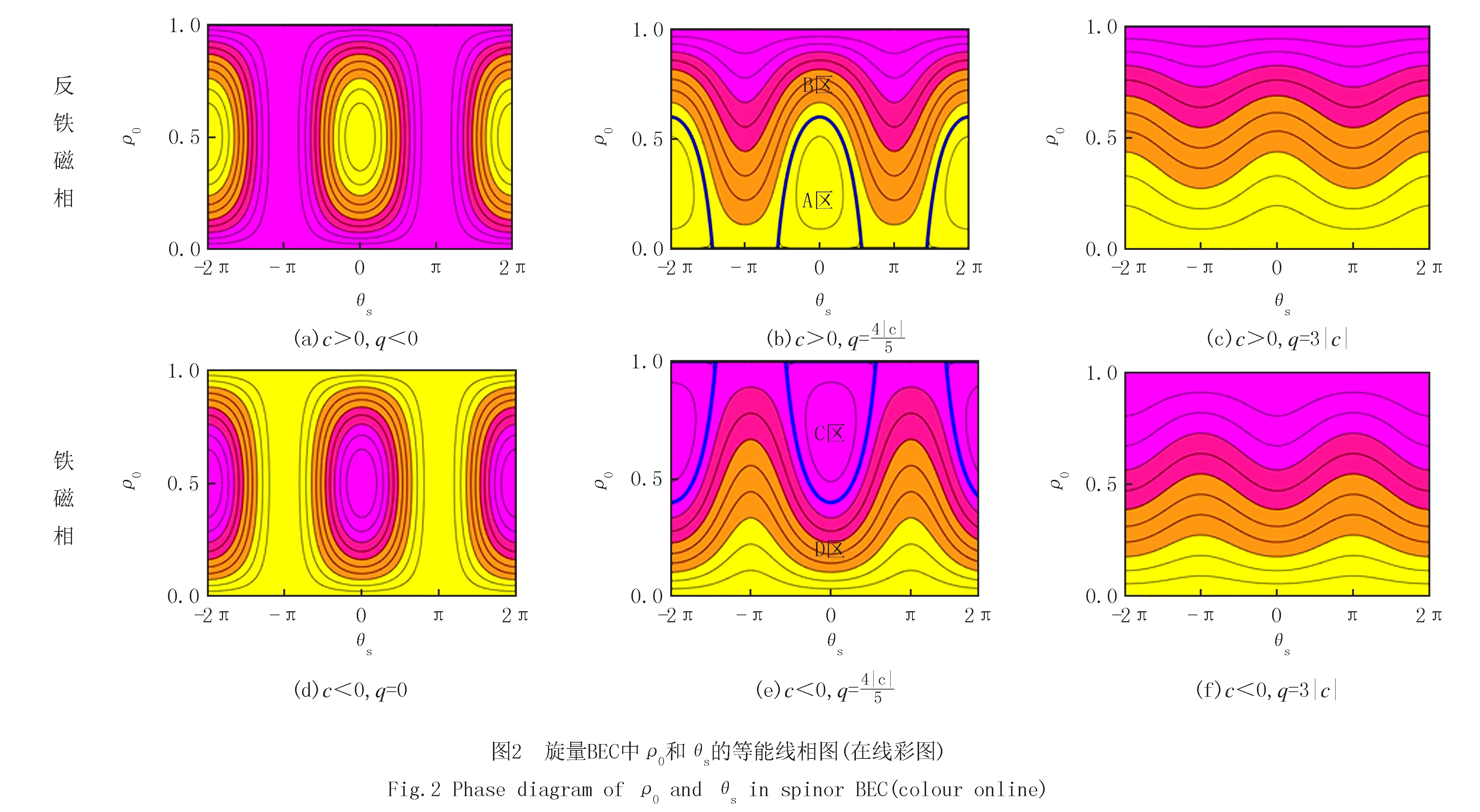
當2個區域都存在的時候，就會有分離線的存在.c<0,q>0時，分離線對應ε=0的等能線，ρ0=1對應系統的不穩定點；c>0,q>0時，分離線對應ε=q的等能線，ρ0=0對應系統的不穩定點.等能線的相圖可以用于預測初態未來的演化趨勢[23].

然而，平均場方法是在粒子數趨向于無窮大并忽略量子起伏的情況下得到的.顯然，在粒子數有限的情況下，與量子相關的性質，如壓縮、漲落等無法通過平均場方法體現.雖然全量子方法可以很好地描述量子性質，但是其計算效率較低.當原子數目比較多時，全量子方法可能會達到計算機極限.而半經典的截斷維格納近似方法[30]結合了平均場方法的思路和全量子中的漲落特點，用一個維格納分布代替一個點來描述初態.這在解決壓縮這類問題中展現出巨大的優勢.既能保證計算速度，又可以準確地描述系統的量子特性[31-32].

2 向列壓縮

在研究自旋壓縮的時候，通常會定義自旋算符

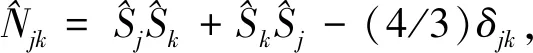
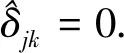
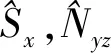
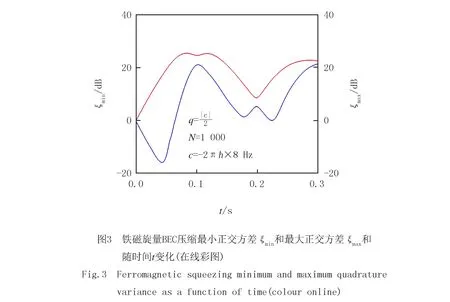
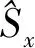
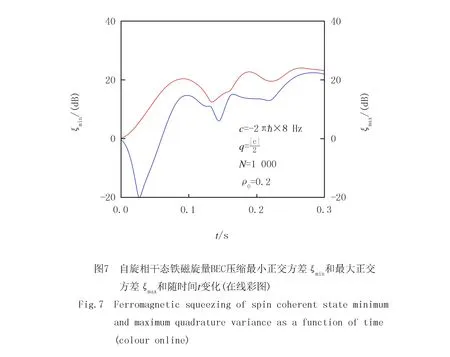
應用變換ξ→10lgξ，相應地，ξmin≥0 dB代表沒有壓縮；ξmin<0 dB代表發生了壓縮，且ξmin的值越小，代表壓縮越明顯.可以看出，初始的時候ξmin=0 dB，代表沒有壓縮，隨著時間演化，最小正交方差不斷變小，直至t=43 ms,最小正交方差達到最小值，隨后壓縮仍然持續一段時間，但是壓縮強度逐漸變小.

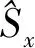
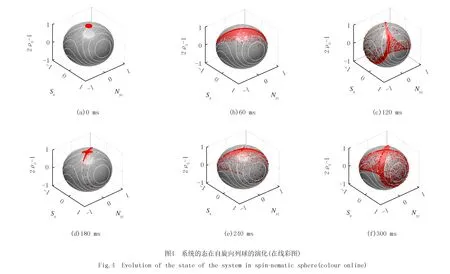
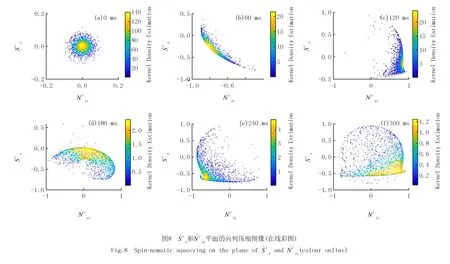
如圖4(a),初始時刻態是一個在球體北極的圓形分布.圖中白色的線是等能線，其中穿過上頂點(不穩定點)(0，0，1)的等能線對應相圖的分離線.將初態制備在不穩定點，隨著時間變化態會沿著分離線壓縮，成為一條細長的曲線.然后散點會沿著分離線散開(圖4(c)).在180 ms時，散點開始沿著分界線的另一支壓縮，在北極處形成交叉的圖像.隨著壓縮的減弱，散點最終散開，但是并非完全散開，而是集中在分離線所在的曲面上(圖4(f)).將圖4中的一系列圖像進行投影，使用顏色標記散點的密度，得到圖5.

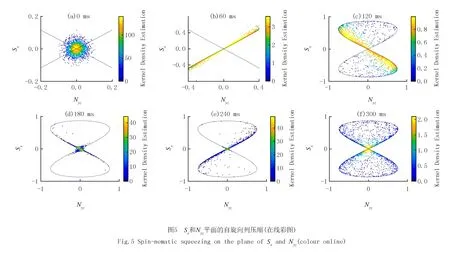
在圖5中，黃色代表散點的密度較大，其次是綠色和藍色.從投影圖可以更加直接觀測到Sx和Nyz.初始時刻，Sx和Nyz的分布近似是一個圓，說明此時沒有發生壓縮.隨著時間的演化，在60 ms時，Sx和Nyz的分布集中在一條線上，且這條線是與分離線重合的，說明此時沿著分離線發生了壓縮，并且壓縮越強，散點構成的區域面積越小，幾乎完全分布在分離線上；相反，壓縮越弱，散點逐漸分散(圖5(c)).Sx的漲落小于Nyz的漲落，說明對Sx有更加準確的測量.在180 ms時，在圖5(d)中散點開始沿著分離線的另一支壓縮.圖5(f)和圖5(c)的形狀相似，但是顏色分布有較大的差別，圖5(c)中黃色區域集中在中心和分離線上，而圖5(f)中黃色區域較少且只集中在中心，藍色區域散布在分離線圍成的閉合圖形中，此時壓縮強度較弱.由此可見，制備在不穩點的初態總是沿著分離線壓縮的.

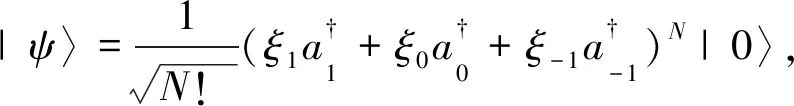
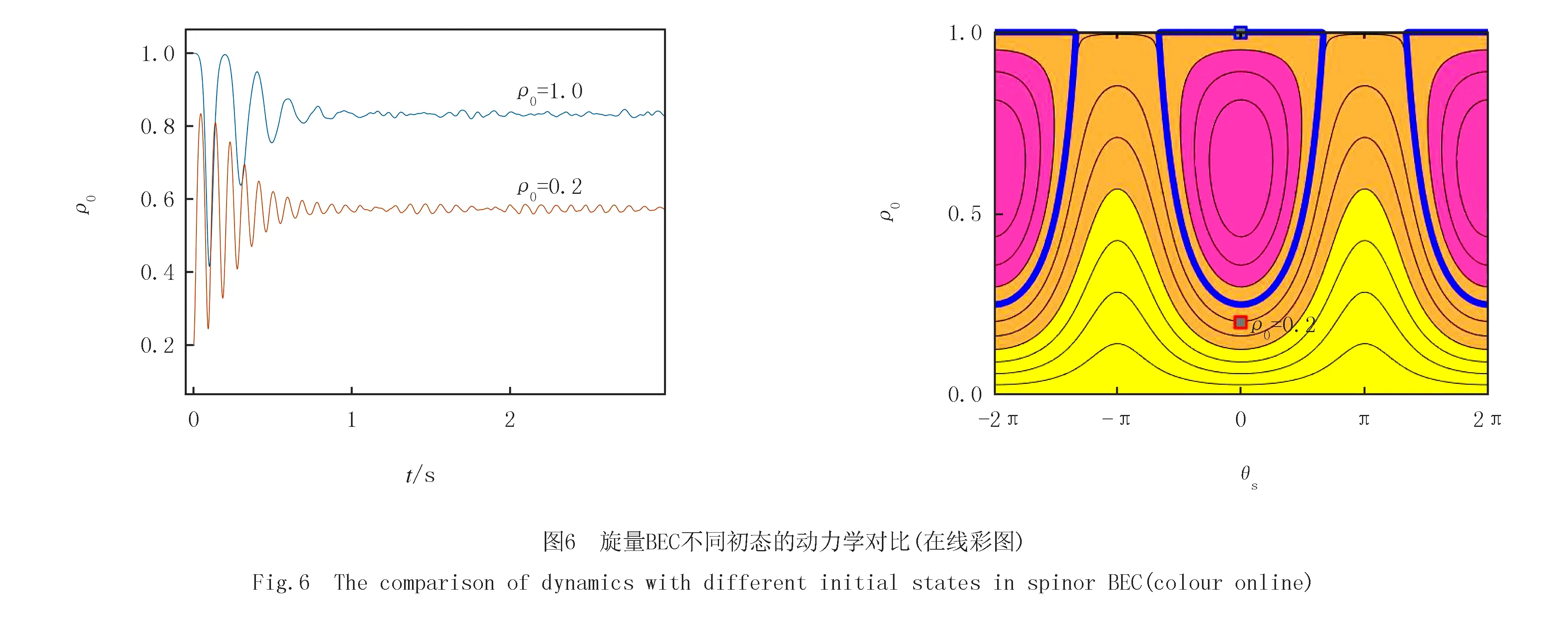
在旋量BEC的鐵磁相(c<0,q>0)中，不穩定點往往對應ρ0=1的極化態，圖6(a)中給出了初態為ρ0=0.2的自旋相干態和初態為ρ0=1的極化態隨時間演化的動力學圖像，可以看到兩種初態最終都趨向于穩態，趨于穩態的時間略有不同，圖6(b)則標出了不同的初態在相圖的位置.

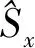
3 總 結

本文從理論上回顧了旋量BEC系統中的自旋向列壓縮特性，推導出了向列壓縮參數的形式，并從數值上模擬了在不穩定點對應的態隨時間演化的規律.通過模擬自旋向列球及其投影圖更清楚地展示了旋量BEC系統中豐富的向列壓縮特性.并且，還研究了任意初態情況下系統的壓縮性質，發現某些自旋相干態的壓縮效果比極化態更佳.