共軸多組充退磁線圈均勻磁場優化設計研究

張健 陳紹露 張紹華 郭濤 劉超波 肖琦

（1 北京宇航系統工程研究所，北京 100076；2 北京衛星環境工程研究所，北京 100094）

0 引言

磁場模擬裝置在航天器磁性控制[1-4]、艦船消磁等領域有著重要的應用[5,6]。磁場線圈是磁場模擬裝置的主要組成部分，中心區域的磁場均勻度是關鍵技術指標之一[7-9]，對其性能有直接影響。方形赫姆霍茲線圈是最簡單的磁場線圈形式，加工制作方便，并且可以通過增加幾何尺寸來滿足均勻區指標要求，但是其代價是線圈常數降低，電源功耗增加，尤其在線圈空間尺寸受到限制時，均勻性指標很難滿足設計要求。所以，在磁場均勻性要求較高，工程安裝空間有限，勵磁電源功耗受限等情況下，可以采用共軸多組線圈組合的方式加以解決。

隨著線圈組數增多，各組線圈尺寸、安裝位置、線圈匝數、電纜截面、電感電阻等參數，存在眾多的組合形式，如果選擇不合理會使得磁場均勻性降低，工程代價增加，甚至不能滿足設計要求。所以，需要結合工程可行性約束條件進行優化設計與計算分析，使其綜合指標性能達到最優。

線圈參數的計算有多種方法，常用的有高階求導法[10,11]、智能優化法[12-16]等。隨著線圈組數的增加，待優化參數也相應增加。張偉等利用磁位的拉普拉斯方程在球坐標系下的解，給出了典型的多段環形線圈的設計方法和過程[7]；對于高階求導法，4對線圈參數優化需要8階求導[10]，9對參數優化需要16階求導[11]，高階求導法十分復雜。呂志峰等針對多線圈均勻磁場優化設計中的高階求導及優化結果可信度評估問題，提出一種基于粒子群優化算法和有限元法相結合的多線圈均勻磁場優化設計方法[12]；王志峰等利用差分進化算法對線圈的均勻磁場進行優化設計[13]。

多組線圈參數的計算問題可以歸結為求解由物理指標（如磁場均勻度指標等）和工程約束條件（如線圈安裝空間等）耦合的目標函數。線圈優化的目標函數中包含非線性函數，是非線性規劃問題。非線性規劃目前還沒有適用于各種問題的一般算法，已有的各種方法都有其特定的適用范圍。序列二次規劃（Sequence quadratic programming，SQP）算法是目前公認的求解約束非線性優化問題最有效的方法之一[17-19]。與其他算法相比，序列二次規劃法的優點是收斂性好、計算效率高、邊界搜索能力強，因此受到了廣泛的重視及應用。本文使用序列二次規劃方法進行共軸多組充退磁線圈系統優化設計，通過優化線圈位置和驅動電流等參數來實現所需的磁場均勻度指標，并且給出了典型的多組矩形線圈在不同工程邊界約束條件下的線圈優化參數、磁場均勻區及電參數的計算結果。

1 線圈參數及磁場計算

方形線圈和圓形線圈是工程中常用的兩種線圈形式。方形線圈具有結構簡單，加工制作方便的優點。不失一般性，本文以共軸正方形多組線圈為例，對磁場分布的均勻性指標進行參數優化研究。

圖1 給出4個方形赫姆霍茲線圈系統及線圈離散單位電流元產生磁場示意圖，坐標原點位于充退磁線圈系統的中心點。4個線圈大小相同，邊長均為a。在實際應用中為保證勵磁電流的同步性，4個線圈串聯，通過電流為I，并假定逆著x軸正方向看電流是逆時針方向。需要說明的是，雖然每個矩形線圈的尺寸可以不同，但是考慮實際加工制作及工程應用，通常設置為相同的大小尺寸。為了滿足軸向整體磁場的對稱性，線圈繞制匝數也成對相等。因此，內側線圈距離d1，線圈匝數相同，均為N1匝；外側線圈距離d2，線圈匝數相同，均為N2匝。預先固定線圈邊長a，需要優化的線圈參數有三組，即d1，d2和內外線圈電流比例（即，ck12=N1/N2）。隨著線圈匝數增多，相應的待優化參數增加。

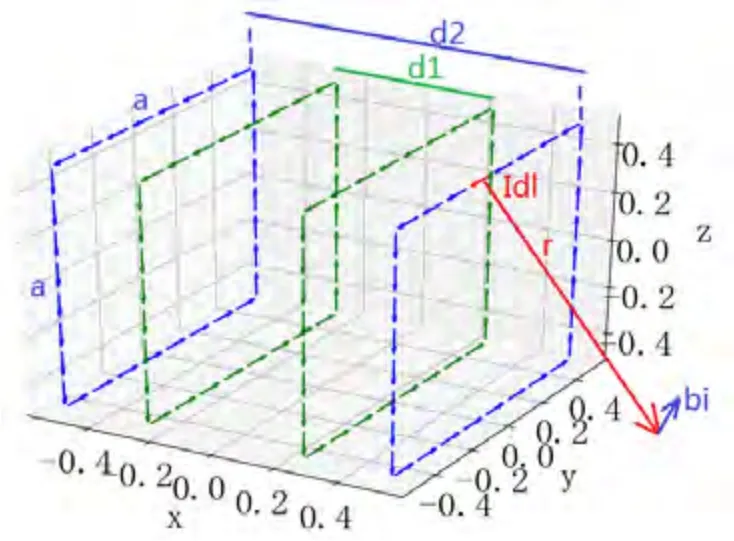
圖1 4個方形赫姆霍茲線圈系統及線圈離散單位電流元產生磁場示意圖Fig.1 Schematic diagram of 4 square Helmholtz coil systems and coil discrete unit current elements to generate magnetic field

優化時需要計算線圈系統在優化區域內多個空間點的磁場。對于方形線圈的磁場計算有很多種方法。解析法在中軸線上的磁場計算相對簡單，但是偏離中軸線的磁場矢量解析公式非常復雜。有限元方法在計算大尺寸空心線圈的三維空間磁場時，對于細導線的網格劃分與空間點的網格劃分差別巨大，導致離散網格點過多、計算耗時甚至解不收斂。本文采用離散積分的方法來計算消磁線圈在空間點的磁場分布。把線圈電流等效為理想線電流模型，線圈離散成微小的電流矢量單元，根據畢奧薩伐爾公式，每個電流矢量單元在某個空間點P的磁場矢量計算公式如下：

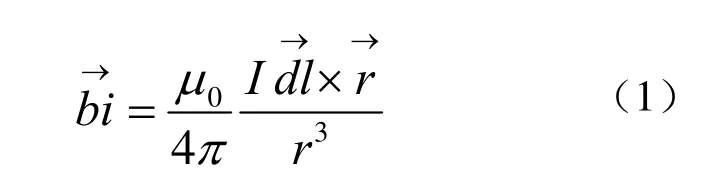
2 優化過程

共軸多組充退磁線圈均勻磁場優化設計過程如下：1）確定線圈組數及待優化參數；2）給出磁場均勻度的目標函數，并結合工程實際給出物理參數邊界條件；3）采用序列二次規劃優化算法對目標函數進行迭代尋優；4）線圈匝數取整化，再次尋優計算；5）數值仿真驗證指標。

2.1 確定線圈組數及待優化參數

優化設計首先需要確定充退磁線圈所采用的線圈組數及對應的待優化參數，通常待優化參數隨著線圈匝數增多而增多。例如：4線圈系統待優化參數有3個，即內線圈距離d1、外線圈距離d2及內外線圈電流比例ck12；6線圈系統的優化參數增加為5個，即內中外三對線圈的距離d1、d2、d3，中線圈與最內線圈電流比ck12，最外線圈與最內線圈電流比ck13。

2.2 定義磁場均勻度指標目標函數

一般采用磁場偏差來衡量磁場均勻度指標大小，磁場偏差值越小，表明磁場均勻度越好。在考察空間內取m個計算點，以線圈系統中心的磁場強度B0為參考，第i個考察空間點的磁場偏差定義為：

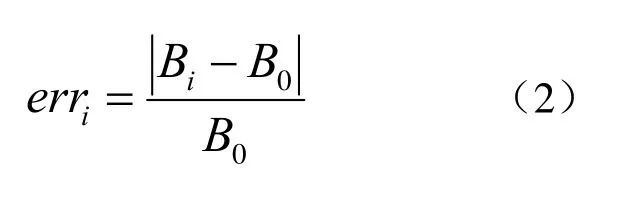
本文采用磁場平均相對誤差作為磁場均勻度指標的目標函數，平均相對磁場偏差定義為：

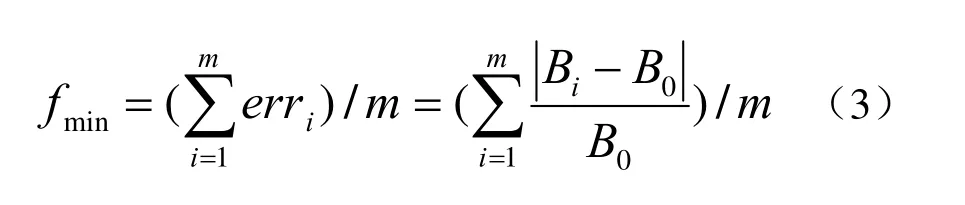
式（3）中，m為網格點總數。根據式（3），可以引入平均相對磁場均勻度指標越大代表磁場均勻度越高。根據2.1知道，對于4線圈系統是關于參數(d1,d2,ck12)的函數，對于6線圈系統是關于參數(d1,d2,d3,ck12,ck13)的函數。實際工程對線圈距離有限制，體現為待優化參數的邊界條件，一般要求d2>d1，d3>d2，d3

2.3 序列二次規劃算法迭代尋優

線圈優化的目標函數 minf是非線性函數，并且通常包含多個約束條件，本文采用的序列二次規劃算法是公認的求解約束非線性優化問題最有效的方法之一。序列二次規劃把問題的求解主要分為兩個步驟：第一步為通過泰勒展開，將原非線性優化問題轉換為簡單的二次優化問題；第二步為對簡單的二次優化（QP）問題進行迭代搜索求解。在序列二次規劃（SQP）的迭代過程中，每一步都需要求解一個或多個二次規劃（QP）子問題。序列二次規劃（SQP）算法流程見圖2，具體算法參考文獻[16-18]。

圖2 序列二次規劃（SQP）優化算法流程圖Fig.2 Sequential Quadratic Programming (SQP) Optimization Algorithm Flowchart

2.4 線圈匝數整數化及二次尋優

線圈匝數需要整數化處理。步驟2.3對于磁場均勻度目標函數 minf計算中以內線圈電流I0=1A為基準，利用2.3中優化參數計算出線圈系統中心磁場強度B0。如果指標要求的中心點最大磁場強度為Bmax，勵磁電源系統允許的最大電流為Imax，那么Bmax/B0就是線圈系統的安匝數，N1=Bmax/（B0*Imax）就是系統最內線圈組單個線圈的匝數，N2=N1/ck12=Bmax/（B0*Imax*ck12）是第2個線圈組單個線圈的匝數，N3=N1/ck13=Bmax/（B0*Imax*ck13）是3個線圈組單個線圈的匝數。這里用迭代尋優線圈電流比例系數計算得到的線圈匝數（N1、N2、N3）通常不是整數，而實際加工繞制都是以整數繞制的，所以需要對線圈匝數進行整數化處理。為保證線圈中心最大磁場強度，一般需要對小數向上取整。線圈匝數整數化之后，其它線圈參數就不是最優了，因此需要固定線圈匝數整數化后的電流比例，對其它的可變參數以步驟2.3的結果為初始值，并在較小區域范圍內進行二次尋優計算，得到最終線圈系統最優參數。

2.5 線圈系統均勻性指標驗證

通過以上過程計算得到線圈系統的最優參數后，需要進行數值仿真計算，檢驗在該參數條件下磁場的均勻性指標是否滿足技術指標要求。此外，需要綜合考慮其它工程約束條件是否滿足，如線圈系統電阻、電源最大功耗、電纜總重量等。如果不滿足，則需要調整線圈系統的約束條件，如線圈個數或者線圈組合形式等，重新進行優化計算。在線圈加工過程中受到加工精度、加工公差及線圈繞制精度的影響，實際的磁場均勻度指標可能會與理論仿真計算結果有一定偏差，所以對于目標函數的優化計算一般需要留有一定余量，例如，如果某區域的目標函數是平均相對磁場均勻度 %100)1(min×-f不低于90%，也就是平均相對磁場偏差 minf<10%，在理論計算中可設置稍微嚴苛一些，如要求目標函數 minf必須不大于8%，為工程加工留有2%的余量。

3 線圈設計實例

結合工程應用，給出一個共軸6線圈充退磁系統的設計實例。為了給某系列包絡尺寸不大于2m的衛星充退磁，要求設計一個空間尺寸長寬高不大于3m的方形共軸赫姆霍茲充退磁線圈系統，最大線圈間距3m，中心待考察衛星工作區域2m×2m×2m立方體均勻區的磁場均勻度不低于95%，中心點最大磁場強度不低于5mT，電源峰值電流不大于100A，充退磁勵磁電源最大功耗不大于40kW。

下面給出該設計實例的優化計算過程及結果。根據普遍采用的方式，優化前的線圈寬度a=3m，6個線圈等間距（線圈間距3/5m），電流相等。設計優化計算中采用平均相對磁場偏差函數作為優化目標函數，以待考察中心區域的總體磁場偏差作為優化目標，而不是只考慮某一個點的磁場偏差。

表1給出了優化前、初次優化及線圈匝數取整二次優化的參數結果。優化前采用最常用的線圈參數，即6線圈等間距分布，匝數相等，d1=3/5m，d2=9/5m，d3=3m，ck12=1，ck13=1，中心待考察的2m×2m×2m立方體區域內的平均相對磁場偏差值為0.073428，最低均勻度為88.22%。初次優化后得到的最優線圈參數，d1=0.4426m，d2=1.3610m，d3=3m，ck12=0.8827，ck13=0.2630，中心待考察的2m×2m×2m立方體區域內的平均相對磁場偏差值為0.003259，最低均勻度為95.95%。優化前與初次優化對比，看出預定區域內的平均相對磁場偏差降低到了優化前的1/23，表明區域內的整體磁場均勻度都得到了很大提高。同時，預定區域內的最低磁場均勻度也由88.22%提高到95.95%。

表1 參數計算結果對比Table 1 Comparison of parameter calculation results

3.1 線圈匝數整數化處理

要求的中心磁場強度為5mT（即5000000nT），優化前單位電流（1A）得到的線圈常數為1536.58nT，最大允許電流為100A，則單個線圈匝數5000000/1536.58/100=32.53，取整為33匝，6個線圈共198匝；初次優化，以最內線圈通電1A為基準，計算得到的線圈常數是2579.58，所以計算得到充退磁線圈系統最內、中間、最外三組線圈的匝數分別為N1=5000000/2579.58/100=19.38，N2=N1/ck12=19.38/0.8827=21.95，N3=N1/ ck13= 19.38/0.2630=73.69。對稱線圈匝數向上取整數之后，N1=20匝，N2=22匝，N3=74匝，線圈系統的總匝數為2×(N1+N2+N3)=232匝。

線圈匝數整數化之后，對于線圈距離參數進行二次尋優，得到d1=0.4272m，d2=1.3753m，d3=3m，ck12=20/22=0.86956，ck13=20/74=0.27027，中心待考察的2m×2m×2m立方體區域內的平均相對磁場偏差值為0.004858，最低均勻度為96.26%。線圈匝數取整并二次優化之后與初次優化相比較，最內與中間線圈組的間距d1與d2有稍微調整，平均相對磁場偏差值從0.003259增加到0.004858，符合預期。

圖3是沿著線圈中心軸x=[-1m，1m]范圍內，優化前、初次優化及線圈匝數取整二次優化的磁場均勻度對比圖，虛線是優化前線圈等間距、等電流（匝數）的計算結果，實線是初次優化之后的結果，虛點線是匝數整數化之后二次優化的結果。由圖2可知，優化前線圈系統在中心軸的磁場均勻度分布極其不均勻，不能滿足技術指標要求，只有在x=[-0.6m，0.6m]范圍內大于95%。初次優化后，在線圈中心軸x=[-1m，1m]區域范圍內磁場均勻度整體提高到97.5%以上。在線圈匝數取整二次優化之后，均勻度稍微降低，但整體均勻度變化不大，仍然在97.5%以上。

圖4中的子圖（a）（b）（c）分別是優化前、初次優化及線圈匝數取整二次優化在中心區2m×2m×2m立方體表面的磁場均勻度分布圖。圖中的方框是6個方形線圈的位置，給出了中心區立方體6個表面的磁場均勻度等值面分布圖。由圖3（a）看出，待考察的立方體區域表面最低磁場均勻度88.22%，并且大部分表面磁場均勻度值低于90%，不滿足磁場均勻度95%的指標要求。從圖4（b）、（c）看出，全部區域滿足磁場均勻度大于95%的指標要求；磁場均勻度在立方體的8個角點附近相對略差，其值大約在96%附近，這也符合矩形線圈在角點附近的磁場均勻度偏差的普遍規律。在4個側面的大部分區域磁場均勻度在98.9%以上。所以，線圈系統優化之后整體磁場均勻度分布有顯著提高，更能滿足充退磁線圈對于中心工作區域的均勻度指標要求。

圖3 沿著線圈中心軸x=[-1m，1m]范圍內，優化前、初次優化及線圈匝數取整二次優化的磁場均勻度對比Fig.3 Along the coil central axis x=[-1m, 1m], the comparison of the magnetic field uniformity before optimization, the first optimization and the second optimization of the rounded number of coil turns

圖4 均勻區磁場均勻度分布圖，a）b）c）分別是優化前、初次優化及線圈匝數取整二次優化的結果Fig.4: The distribution diagram of the uniformity of the magnetic field in the uniform area, a) b) c) are the results of the optimization before optimization, the first optimization and the second optimization of coil turns

3.2 線圈電參數計算

線圈尺寸優化設計完成后，需要根據充退磁電源允許的峰值電流和最大功耗等參數，選取電纜的尺寸，估算線圈電纜總電阻、總重量、電源功耗等。本設計方案允許的最大電流為100A，根據經驗選取直徑4mm的漆包銅線作為繞線電纜。銅線電阻率ρ通常取值1.75×10-8Ω/m，銅線電阻計算公式如下：

式（4）中a為方形線圈寬度，Nc為線圈系統總匝數，d為銅線直徑取值4×10-3m。

分別對優化前及匝數取整二次優化的線圈物理常量進行計算，表2給出線圈物理常量的計算結果對比。得到優化前（Nc=198匝）的充退磁線圈參數：長度2376.00m，電阻3.31Ω，功耗33.09kW，重量265.73kg；線圈匝數取整二次優化（Nc=232匝）的充退磁線圈參數：長度2784.00m，電阻3.87Ω，功耗38.77kW，重量311.36kg。雖然優化設計后的線圈系統匝數、功耗與重量增加約17.2%，但是在中心待考察衛星工作區（2m×2m×2m立方體區域）的平均相對磁場偏差降低到了優化前的1/23，整體磁場均勻度得到了極大提升。

表2 線圈物理常量計算結果對比Table2 Comparison of calculation results of coil physical constants

4 結論

本文基于序列二次規劃（SQP）方法，對共軸多組充退磁線圈進行系統優化設計。用離散積分的方法計算消磁線圈在空間點的磁場，以待考察區域的平均相對磁場偏差作為優化目標函數，并考慮工程約束條件，優化計算出不同線圈位置和驅動電流等參數。對線圈匝數整數化后進行二次優化，提高了均勻區的指標。結合一個實際工程中的共軸6線圈系統設計案例，給出了詳細的優化步驟及結果，對于線圈匝數取整及二次尋優有詳細闡述。仿真計算結果表明，經過優化設計后的共軸充退磁線圈系統的磁場均勻度得到了極大提升，在中心待考察衛星工作區的平均相對磁場偏差降低到了優化前的1/23，其它電參數均能滿足技術指標要求。