基于浮動基座偏載發射的初始擾動影響分析

陳苗 姜蘇洋 張博宇 弓韜 孟艷

(1 北京航天發射技術研究所，北京，100076；2 火箭軍裝備部駐北京地區第一軍事代表室，北京，100076）

0 引言

隨著作戰樣式和發射方式的不斷變化，發射地點的選擇范圍也隨之擴大以增加武器裝備的機動性能、隱蔽性能和打擊范圍。發射地點的結構強度和穩定性會對直接影響作用到發射裝置上的載荷，由此會影響導彈發射的初始擾動。

目前，發射地點的選擇趨于多樣化，國內外諸多學者關于發射地點對導彈初始擾動的影響研究也隨之進行。趙風成[1]對艦載武器建立全剛體動力學模型，在不同海況作用下的導彈出筒姿態進行仿真分析；劉榮華等[2]對某型路基行進間發射武器系統建立剛柔耦合動力學模型，分析不同瞄準精度下導彈的發射精度；廖莎莎[3]應用ADAMS軟件建立了“捕食者”機載導彈發射系統動力學模型，得出了機載導彈初始擾動與載機之間的影響規律；魏昕林[4]以有限元接觸理論為基礎建立了機載導彈水平向后發射的有限元模型，結合載機周圍流場分析，得到了不同發射影響因素對機載導彈初始擾動的影響；董曉彤[5]通過非線性有限元動力學數值計算，分析了發動機推力偏心、地面傾斜度等不同發射工況對車載雙聯裝發射平臺前后兩發彈發射精度和發射平臺穩定性的影響規律；發射箱口的下沉直影響彈體的初始擾動，李璞等學者[6]結合實際產品的實測數據對發射箱口下沉規律進行研究；風載荷會直接影響發射車系統的穩定性，從而影響導彈的出筒姿態，劉瑞卿等學者[7]基于流固耦合方法針對大型車載垂直發射系統進行了穩定性影響分析；機載武器在發射過程中載機的自身力學環境和空氣動力耦合作用會對導彈的初始擾動產生直接影響，高慶等學者[8]建立了氣-剛-柔多場耦合系統分析模型，同時結合試驗數據分析確定了機載武器彈性的影響。

本文以某型浮動基座發射平臺偏載發射為研究對象，通過建立剛柔耦合系統動力學模型，對偏載發射情況下彈體出筒姿態進行仿真，仿真結果經過試驗驗證仿真可信度90%以上。基于仿真結果和試驗數據分析浮動平臺結構剛度與偏載發射耦合作用對彈體初始擾動的影響，以指導后續相關方案設計和優化。

1 發射動力學建模

1.1 模型建立原則

在進行發射動力學仿真分析時，根據計算工況需對仿真模型進行簡化處理[9]，實際導彈發射時，運載體裝載筒彈組合體支撐在浮動基座發射平臺上，考慮浮動平臺本身的剛度特性，將浮動平臺的支撐剛度特性簡化為彈簧阻尼模擬，彈體按剛體模擬。仿真模型簡化為浮動平臺本體、發射筒、彈體、運載體架體四個分系統，仿真模擬發射角度為94°，最終將模型簡化為剛柔耦合的彈-架系統動力學仿真模型。

按照幾何建模、賦予材料屬性、建立約束關系、施加載荷和邊界條件、仿真結果判讀、根據試驗結果模型修正、系統仿真分析的步驟建立基于剛柔耦合方法的發射系統動力學仿真模型，對應的原則如下：a)按真實參數建立發射筒、彈體、浮動平臺、運載體的三維模型，并使各部件模型及相關參數（質量、質心、轉動慣量等）與設計一致；b)模型裝配關系與實際產品裝配關系一致；c)忽略緊固件等不傳遞運動、不起支撐作用的小部件；d)對部件中的倒角、螺紋孔等影響網格質量的部位進行簡化處理；e)模型中僅將彈體考慮為剛體，其余均為柔性體；f)模型中各類約束關系均當做理想約束處理，不添加摩擦因素。

1.2 建模過程及拓撲關系

通過三維建模軟件Creo建立各部件的三維幾何模型并進行裝配，導入Abaqus后對各部件賦予材料屬性、建立約束關系、施加載荷和邊界條件、劃分網格，由此建立剛柔耦合動力學仿真模型，各部件之間的拓撲關系如圖1所示，各部件之間的位置關系如圖2所示。浮動平臺有四個支撐點位，單個支撐點位的支撐剛度為9000N/mm。

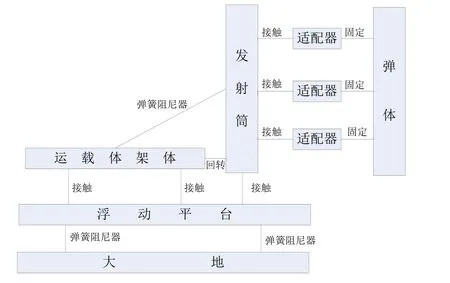
圖1 各部件拓撲關系圖Fig.1 Topology diagram

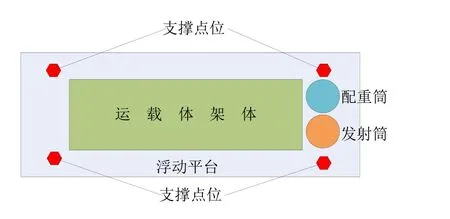
圖2 各部件位置關系圖Fig.2 Location diagram

仿真坐標系說明：發射原點為回轉支耳中心線與縱向對稱面交點，X軸正方向為縱向，與運載體前進方向相同；Y軸正方向為側向，即水平向右（沿車行進方向看）；Z軸正方向為垂向，即垂直于地面為豎直向下。

2 發射過程仿真分析

2.1 仿真可信性分析

對導彈發射過程進行動力學仿真分析，彈體在推力作用下出筒，結合實際試驗的高速攝像結果和其他實測數據修正仿真模型，同時分析浮動平臺結構剛度與偏載發射耦合作用對彈體初始擾動影響。

對彈體而言，初始擾動的主要影響因素之一就是彈架系統的振動影響彈體的姿態角度和角速度，為更有效的評估仿真可信性，采用試驗數據與仿真數據對比進行驗證。驗證的內容包括筒口振動和彈體出筒姿態，試驗過程中彈體在0.6s出筒，因此主要分析0s～0.6s的試驗數據。發射筒口振動測點布置如圖 3所示。

圖3 振動傳感器安裝位置示意圖Fig.3 Vibration sensor installation position diagram

據安裝電容加速度傳感器，電容加速度傳感器具備過載測試功能，數據處理對筒口振動曲線進行平滑濾波處理，提取趨勢性項數據即為筒口過載加速度數據，處理后數據曲線如圖 4～圖 6所示。

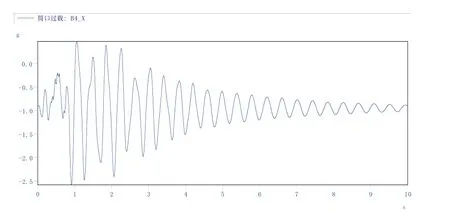
圖4 筒口x向振動Fig.4 X direction vibration of canister head

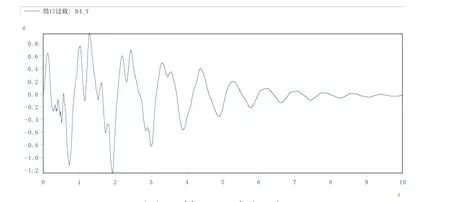
圖5 筒口y向振動Fig.5 Y direction vibration of canister head

圖6 筒口z向振動Fig.6 Z direction vibration of canister head

彈體出筒時刻筒口過載加速度對比情況如表 1所示。

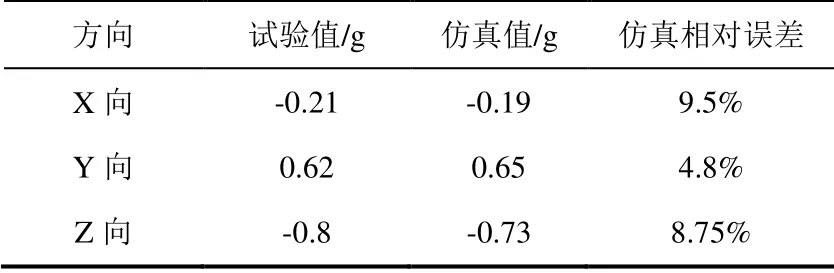
表1 彈體出筒時刻筒口過載加速度對比Table1 Acceleration of canister head

因為偏載發射工況，導致發射過程中在發射載荷作用下浮動平臺左側支撐裝置壓縮，導致整體出現側向偏移，因此筒口Y向和Z向過載較大。

根據高速攝影結果分析，彈體出筒時的角速度為3.153°/s；根據仿真分析結果，彈體出筒瞬間，筒口側向速度0.2m/s，彈體質心側向速度0.18m/s，角速度3.10°/s。由此角速度仿真誤差1.68%。

圖7 高速攝像結果Fig.7 High speed photography diagram

根據高速攝影判讀，彈體出筒瞬間筒口側向偏移271mm、垂向下沉56mm；根據仿真結果，彈體出筒瞬間筒口側向偏移251mm、垂向下沉52mm。側向偏移仿真誤差在7.4%，垂向偏移仿真誤差在7.1%。

圖8 筒口偏移情況Fig.8 Deviation of canister head

通過試驗結果與仿真結果對比分析，仿真結果與試驗數據吻合良好，誤差在10%以內，仿真模型準確，仿真結果可信。

2.2 浮動平臺對出筒影響分析

為對比浮動平臺偏載發射對彈體初始擾動的影響，對比分析浮動平臺偏載發射和普通硬質場坪發射的仿真結果。因為浮動平臺為偏載發射，所以主要對比彈體側向姿態和筒口的側向變化情況。

仿真設置中前1s為靜平衡階段，第1s開始發射載荷開始作用，隨即彈體在0.6s完全出筒，因此后續仿真結果主要對比1s～1.7s的數據。

2.2.1 彈體出筒角度對比

彈體出筒側向角度對比如圖 9所示，硬質場坪發射時最大側向角度為0.258°，浮動平臺偏載發射時最大側向角度為1.223°，由此浮動平臺偏載發射下角度增加374%。

圖9 彈體出筒側向角度對比Fig.9 Lateral angle comparison

2.2.2 彈體出筒角速度對比

彈體出筒側向角度對比如圖 10所示，硬質場坪發射時出筒側向角速度為0.84°/s，浮動平臺偏載發射時出筒側向角速度為2.8°/s，由此浮動平臺偏載發射下出筒角速度增加233%。

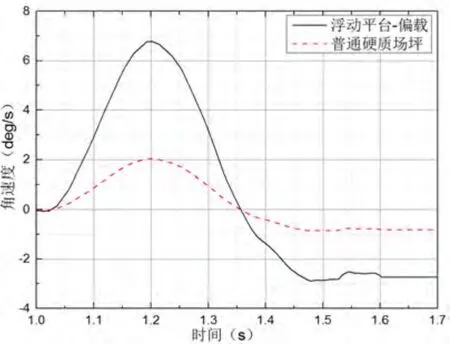
圖10 彈體出筒側向角速度對比Fig.10 Lateral angle speed comparison

硬質場坪發射過程中最大側向角速度為2.03°/s，浮動平臺偏載發射過程中最大側向角速度為6.8°/s，由此浮動平臺偏載發射下出筒過程最大角速度增加207%。

2.2.3 彈體出筒角加速度對比

彈體出筒側向角度對比如圖 11所示，硬質場坪發射時最大側向角加速度為18.35°/s2，浮動平臺偏載發射時最大側向角加速度為67.03°/s2，由此浮動平臺偏載發射下側向角加速度增加265%。

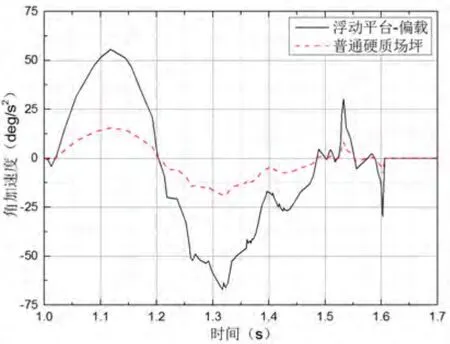
圖11 彈體出筒側向角加速度對比Fig.11 Lateral angle acceleration comparison

2.2.4 筒口位移變化

因為是偏載發射工況，因此重點關注發射筒筒口側向位移情況，具體如圖 12和圖 13所示。

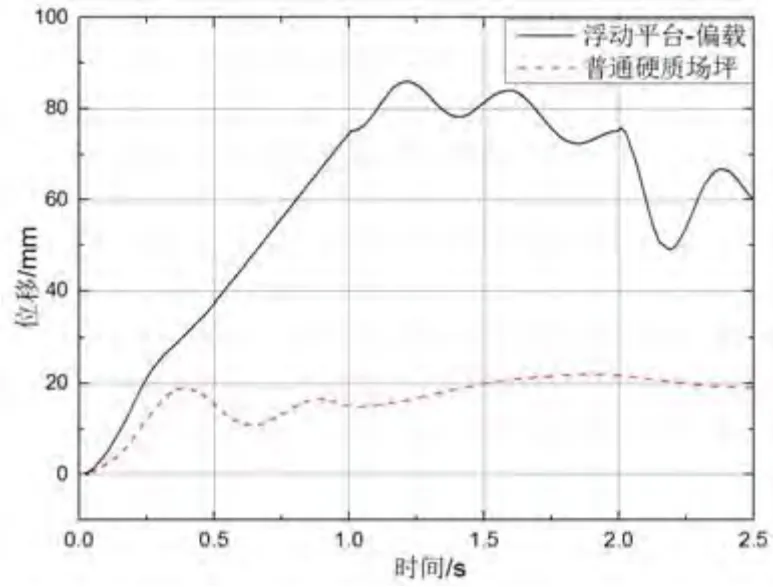
圖12 彈體出筒過程筒口垂向位移Fig.12 Vertical position of canister head

圖13 彈體出筒過程筒口側向位移Fig.13 Lateral position of canister head

浮動場坪偏載發射工況在靜平衡階段發射筒口垂向下沉75mm、側向偏移17.8mm，這是由于浮動平臺支撐剛度和偏載工況引起的。發射過程中，在發射載荷作用下發射筒口的側向偏移量為26.5mm，垂向下沉12mm，彈射結束后相比于初始位置，發射筒筒口垂向上移17mm。

硬質場坪發射工況在靜平衡階段發射筒口垂向下沉14.7mm、側向偏移0.299mm。發射過程中，在發射載荷作用下發射筒口的側向偏移量為13.26mm，垂向下沉7.3mm。

3 結論

a)本文以某型浮動基座發射平臺偏載發射為研究對象，建立剛柔耦合系統動力學模型，經試驗驗證仿真誤差小于9.5%，仿真模型真實有效。

b)通過對比分析浮動平臺偏載發射工況和硬質場坪地面發射工況，前者主要影響彈體側向出筒姿態，前者的側向出筒角度增加374%、角速度增加233%、角加速度增加265%。

c)在浮動平臺支撐剛度和偏載發射耦合作用下，發射過程中發射筒出現較大側向偏移，由此引起彈體出筒姿態的變化。