新課標引領下“指數函數與對數函數”單元教學剖析
——以人教A版教材為例

哈爾濱師范大學教師教育學院 劉金煥

《普通高中數學課程標準(2017年版)》(以下簡稱《標準》)頒布后，各版本新教材紛紛亮相.《標準》中的課程理念和課程目標為中學數學教學指明了新的方向，同時也要求廣大數學教育工作者在新課標視角下解讀新教材，挖掘其育人價值.

高中數學課程分為四條主線：函數，幾何與代數，概率與統計，數學建模活動與數學探究活動[1].函數作為描述客觀世界中變量關系和規律最為基本的數學語言和工具，是高中數學課程的重要內容.而“指數函數與對數函數”單元又是函數主線的重要組成部分，有著廣泛的應用，所以在新課標引領下，以人教A版《普通高中教科書· 數學》必修第一冊(以下簡稱“教材”)為研究對象，對此單元進行分析，并分享一些教學啟示.

1 章節編排與知識框圖

1.1 章節編排

“指數函數與對數函數”章節編排見表1.由表可看出，章節分布非常明晰，先進行基礎知識的學習，而后是綜合應用.

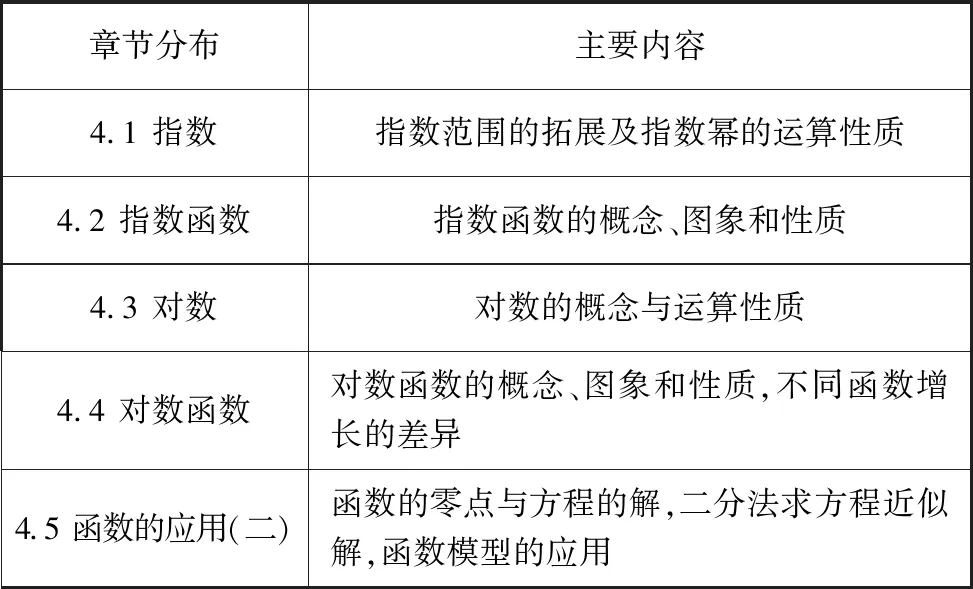
表1 指數函數與對數函數章節編排

知識分為兩塊：指數函數與對數函數.每一類函數前都編排了相應的支架知識：指數，對數.而學生之前已經接觸過指數，對數是一種新的代數對象，它與指數可以互化，所以將指數與指數函數安排在對數與對數函數之前.

教材很重視應用，不僅本單元末尾設置了“函數的應用”，在每一節的每一知識塊后都配備了練習，突出即學即用的特點.此外，函數的應用既包括數學內部的應用，又包括現實生活中的應用，多角度詮釋數學的價值.

1.2 知識框圖

“指數函數與對數函數”單元中數學知識互相關聯，知識框圖如圖1.

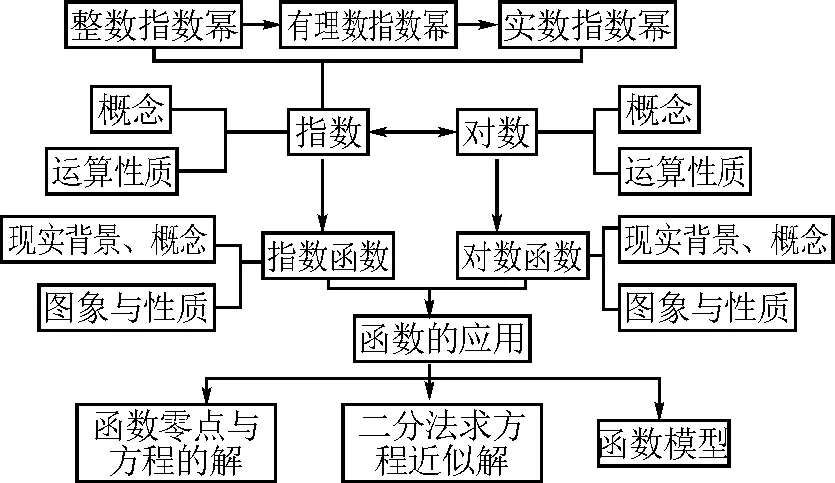
圖1

2 主要內容剖析

2.1 指數

(1)主要內容

初中已學過整數指數冪，教材以此為生長點引入n次方根并推出其基本性質，進而定義分數指數冪，給出有理數指數冪的運算性質；而指數由有理數拓展到實數運用了逼近思想.指數的拓展為指數函數(尤指定義域)做鋪墊，且指數冪的運算性質對指數函數也適用.

經歷指數拓展的過程，體會變化中的不變性，并通過指數冪運算性質的運用進一步熟悉分數指數冪、無理數指數冪，熟練掌握指數冪的運算性質，為指數函數和對數的學習打基礎，提升邏輯推理、數學運算素養.

(2)內容剖析

指數拓展過程中既有變化，又有不變性，變的是指數的范圍，不變的是運算性質.其實，指數范圍拓展的過程與數系擴充的過程類似.不禁聯想：指數能否為虛數？可以，且eiθ=cosθ+isinθ，這是著名的歐拉公式.

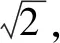
2.2 指數函數

(1)主要內容

概念一節中，從景區游客人次變化(以下稱“情境一”)、生物體內碳14含量變化(以下稱“情境二”)兩個問題情境出發，將其中的變化規律用數學語言表示出來，歸納其共同特征，從而抽象出指數函數的概念，并給出其定義域R，呼應上節課指數的拓展.

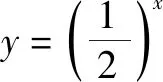
(2)內容剖析

指數范圍拓展到了實數，也研究了冪函數，本章用研究冪函數的過程與方法來研究另一基本初等函數：指數函數.它們都遵循著“背景-概念-圖象與性質-應用”的研究路徑，且都是根據圖象來歸納性質[2].后面學習對數函數、三角函數時也是如此，但三角函數具有周期性，所以還有特殊的方法.

對于情境一，從數據和散點圖兩方面分析游客人次變化趨勢，并結合運算得到B地具體的變化情況，建立合適的模型來描述這種規律.該情境貼近學生生活，易于理解，能激發學生學習熱情，且整個過程相當于一個小型建模活動，能積累數學活動經驗，有效提升數據分析、數學建模、直觀想象、邏輯推理、數學運算素養.情境二與情境一總體上大同小異，但不多余，要抽象出指數函數的概念，并歸納函數的共同特征，至少需兩個函數，所以情境二是必要的，同時還擴充了學生的知識面.

得出函數關系后，歸納其共同特征，進而給出指數函數的概念.此處抽象歸納的過程類比了抽象冪函數概念的過程，能提升學生數學抽象素養和思維的嚴謹性.另外，引入指數函數概念后要引導學生區分指數函數與冪函數.

第一課時難點：情境一如何想到做除法找規律？為什么指數函數中a>0,且a≠1？教學過程中教師要適當引導，激活學生的思維，不可直接告知.

2.3 對數

(1)主要內容

在情境一中拋出問題“經過多少年游客人次是2001年的2倍、3倍？”，從而引入對數的概念，并介紹常用對數和自然對數.根據指數與對數的關系得出對數的基本性質，借助指數冪的運算性質來研究對數的運算性質.換底公式則是為了解決底數不同的對數的運算問題.

學生需明晰對數概念，能進行指數與對數的互化，體會對數簡化運算的作用，能用對數運算性質解決簡單的數學問題和實際問題，為對數函數的學習打基礎.

(2)內容剖析

由指數運算性質推出對數運算性質，教材中有詳細步驟.性質一由小組合作探究完成，性質二、三可由學生嘗試獨立完成.這是訓煉學生數學思維的好機會，設置合適的問題鏈進行引導，讓學生通過自己的努力獲得新知，提升邏輯推理素養，增強學習數學的信心，養成自主思考、合作探究的習慣.

對數是一個新的代數對象，與指數有著類似的研究路徑“背景-概念-性質-運算性質-應用”.教師和學生都應該明確這樣的研究路徑，讓學生不僅學會，還能會學.

重視乘方運算、對數運算、開方運算的關系.如果ab=N，那么a，b，N三者知二可求一[3].若已知a與b，求N，是乘方運算(即求指數冪)；若已知b與N求a，是開方運算；若已知a與N，求b，是對數運算.所以，嚴格來講，乘方運算的逆運算有兩種：一種是開方運算，一種是對數運算[2].另外a，b，N三者確定其一之后，另兩個在滿足一定條件下可構成函數關系.若a確定，則N是b的指數函數(這里a>0,a≠1)；若b確定，則N是a的冪函數.

對數的發展是個漫長的過程，適當滲透相關數學史，可拓寬學生的視野，學生也能感悟到對數的廣泛用途以及數學家們嚴謹求實的科學精神.

2.4 對數函數

(1)主要內容

在情境二中提出問題：死亡時間x是碳14含量的函數嗎？根據指數與對數的關系對函數解析式進行變形，分析圖象抽象出對數函數的概念，明確其定義域.

對數函數的圖象與性質，整體沿用研究指數函數圖象與性質的方法，學生較容易概括出對數函數的性質.此外，需知道反函數的概念，明確底數相同的指數函數和對數函數互為反函數.

學習了冪函數、指數函數與對數函數三種基本初等函數，遇到具體問題該用哪種函數來刻畫呢？所以要研究不同函數增長的差異，充分借助信息技術，讓學生體會“對數增長，直線上升，指數爆炸”的變化特點.

(2)內容剖析

互為反函數的兩個函數，一個函數的定義域是另一函數的值域，而它的值域是另一函數的定義域.學生在大學會更加深入地學習反函數，高中階段，可借助指數函數與對數函數來簡單認識.它們定義域與值域的關系，是從數的角度來看指數函數與對數函數，那么從形的角度來看它們又有什么聯系？可引領學生利用信息技術開展探究活動，使學生體會數形結合思想，積累數學活動經驗.

2.5 函數的應用(二)

(1)主要內容

將預備知識中二次函數與一元二次方程的關系進行推廣：函數y=f(x)的零點是方程f(x)=0的實數解.這其實是將問題進行轉換，滲透了轉化思想、函數思想、方程思想.那函數何時有零點呢？通過探究得到零點存在定理.

零點存在定理只能判斷函數在某區間是否存在零點，如果有零點，具體是幾個則不能確定.介紹求方程近似解的方法——二分法，需引導學生探索二分法求方程近似解的思路并畫出程序框圖，滲透算法化思想，訓練學生的數學思維，提升邏輯推理、數學運算素養.二分法的步驟非常明確，且都是重復的，有時運算量比較大，可設計計算程序借助信息技術來完成.這不僅能讓學生增長見識，體會到信息技術的強大，也為對這方面感興趣的學生提供另一解決問題的途徑.

以上是函數在數學內部的應用，函數在實際生活中也有著廣泛的應用.建立函數模型解決實際問題的內容不容小覷，數學建模已是數學六大核心素養之一，可見它的重要性.這一小節，要讓學生學會如何選擇合適的函數模型刻畫現實問題中的變化規律.

(2)內容剖析

函數零點存在定理看似簡單，實則內涵豐富.“如果函數y=f(x)在區間[a,b]上的圖象是一條連續不斷的曲線，且有f(a)f(b)<0，那么函數y=f(x)在區間(a,b)內至少有一個零點”.需要明確：①兩個條件“連續不斷”“f(a)f(b)<0”都要滿足，結論才是至少有一個零點；②“至少一個零點”，即可能有多個零點，但無法確定個數；③條件是閉區間，結論是開區間，表述很嚴謹，條件暗中表明函數在[a,b]上是有定義的，而f(a)f(b)<0說明f(a)，f(b)不為0，即a，b都不是零點，結論中用開區間很合理，那如果條件中是開區間呢，須保證a，b處有定義才能寫f(a)f(b)，且函數要滿足在a處右連續，b處左連續，此時結論也成立，但這種描述與定理是等價的，且定理更加簡潔；④若條件是f(a)f(b)≤0，能得到什么結論？這時結論需要改成“若f(a)f(b)<0，(a,b)內存在零點，若f(a)f(b)=0，則a或b是零點”；⑤定理的逆命題為假命題.以上均可借助圖形輔助解釋.對零點存在定理要細致解讀，體會數學語言的嚴謹性、簡潔性.

二分法只是求方程近似解的一種方法， 中外還有很多種求解方法，尤其是比較知名的牛頓逼近法，可作為拓展，讓學生自行搜集資料了解相關內容.

建立數學模型解決實際問題是本章的重點內容.教材給出了40多個實際問題，在導入的問題、例題、練習、習題中均有涉及.它們體現了數學與實際生活以及與其他學科的聯系，能提高學生運用模型思想發現和提出問題、分析和解決問題的能力.

3 教學啟示

3.1 明確研究路徑

新一輪課程改革以“數學的整體性、邏輯的連貫性、思想的一致性、方法的普適性、思維的系統性”為追求，強調突出數學本質，不僅要引導學生學會知識，還要引導學生學會學習，為其終身學習提供保障.本單元的學習，要讓學生明確研究一類函數的過程與方法，以及研究代數對象的套路.

3.2 重視數學建模

指數函數和對數函數能刻畫很多實際問題，且與其他學科密切聯系，所以要重視引導學生運用所學知識建立模型解決現實生活中的問題，并與其他學科達到有機地融合.注意把控難度，循序漸進，初始階段解答并適當引申，后期可開展數學建模活動.

3.3 善用信息技術

《標準》指出：要注重信息技術的運用，實現信息技術與數學課程的深度融合，提高教學的實效性.善用信息技術，能使抽象的問題形象化，還能提升課堂效率，提升學生直觀想象素養，培養學生運用其他工具來研究數學問題的意識.比如：研究情境一，可借助信息技術繪制散點圖；研究指數函數與對數函數的圖象性質時借用信息技術畫圖，可以減少工作量，節省時間.

3.4 把握情境“復用”

情境“復用”，是指同樣的問題情境多次出現.但“復用”不是簡單的重復，而是在原有基礎上有所深化，或從另一角度來看待問題，總體而言是螺旋上升的過程.情境“復用”在一定程度上有利于學生融入情境，且從不同角度看待這個情境，學生會有溫故而知新的成就感，還有助于培養多角度看問題的能力.比如本單元中情境一出現在指數函數的概念生成與此節例題中，又用來引出對數的概念，得到換底公式之后又用換底公式解決引入對數時該情境中的問題.

3.5 挖掘教材例、習題的育人價值

教材例習題蘊涵豐富的育人價值，解這些題不僅能鞏固相關的數學知識，還能讓學生體會到數學多方面的價值，激發學習數學的興趣.比如：氫離子濃度和溶液酸堿度的關系，這和化學有聯系；血液中酒精含量的變化，這與生活息息相關，還能滲透法律知識；習題4.5中第6，11題涉及計算機知識；習題4.3中1.01365,0.99365，則是“小問題、大道理”.