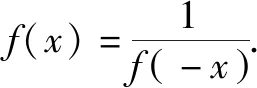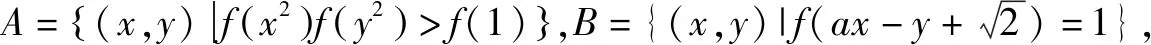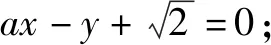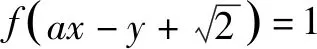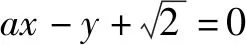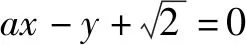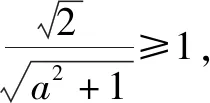三類抽象函數常考題型例析
廈門集美中學 陳習儉
1 f(x+y)=f(x)+f(y)型
求最值問題是有關抽象函數問題常見的一類題型,需要根據函數的自身基本特征求解,例如f(x+y)=f(x)+f(y)類型的抽象函數,可以先構建一次函數(f(x)=kx)進行轉化:①分析函數f(x)的原型解析式,以及該函數的周期性、奇偶性、單調性等;②利用f(x+y)=f(x)+f(y)等基本特征求解,通過構造不等式判斷函數在定義域內的單調性;③具體問題具體分析,結合所知條件得到所求最值.
例1對任意的x,y∈R,函數f(x)均滿足f(x+y)=f(x)+f(y),并且當x<0時,有f(x)>0,f(1)=-3,求函數f(x)在區間[-2,3]上的最大值和最小值.
分析:本題是很明顯的一次函數型抽象函數問題,其中f(x)的原型是y=-3x.猜想該函數是實數集R上單調遞減的奇函數,要求解在區間[-2,3]上的最值,即分析f(-2),f(3)的值.
解:根據題意,得f(0)=0,f(-x)=-f(x),f(2)=2f(1)=-6,f(3)=3f(1)=-9.
令任意x1 f(x1)-f(x2) =f[(x1-x2)+x2]-f(x2) =f(x1-x2)+f(x2)-f(x2) =f(x1-x2). 依題意,由x1-x2<0,得f(x1-x2)>0. 即有f(x1)>f(x2). 所以f(x)在區間[-2,3]上是減函數. 故它的最大值為f(-2)=-f(2)=6,最小值為f(3)=-9. 分析:由于一次函數滿足f(x+y)=f(x)+f(y),可假設函數f(x)=-kx,借助已知條件f(1)=-2求出具體函數解析式,判斷所得解析式是否滿足“當x>0時,f(x)<0”這一條件.最后將所求一次函數解析式代入命題中的不等式中,求出具體解集,即可判斷命題的真假. 解析:設函數f(x)=-kx. 由f(1)=-2,可得k=2. 即f(x)=-2x,且滿足x>0時,f(x)<0. 代入不等式,可得-6x2+4x<-6x+4. 整理,得6x2-10x+4>0. 故所給命題為真命題. 求自變量的值是抽象函數問題的另一類常見題型,也需要利用其函數基本特征求解,例如f(xy)=f(x)f(y)特征類抽象函數,可以構建冪函數型(f(x)=xn)特征函數進行轉化,需要遵循以下思路:①猜想具體函數解析式,根據題設信息分析函數的具體形式,例如f(x)=x-1等;②根據猜想的函數形式判斷對應函數的單調性,并利用單調性解題;③利用函數基本特征解題,即將f(xy)=f(x)f(y)等基本特征與實際問題相結合進行求解. 解:根據題意可知 所以f(x)在區間(0,+∞)是減函數. 又因為f(1)=f2(1),f(x)>0,所以f(1)=1. 又f(m)f(3)=f(3m),所以f(3m)=1=f(1). 變式2已知f(x)在(0,+∞)上都有f(x)>0,且滿足f(xy)=f(x)f(y),f(3)=27,若f(-a2)=-64,則求a的值. 分析:猜測滿足條件f(xy)=f(x)f(y)的函數f(x)為冪函數型,則假設f(x)=xn,利用該條件與f(3)=27推斷函數f(x)的解析式,并判斷函數的奇偶性,然后由f(-a2)=-64,即可得到a的值. 解析:假設函數f(x)=xn. 由f(3)=27,可得f(x)=x3. 則有f(-x)=-f(x). 所以f(-a2)=-f(a)f(a)=-64. 因此f(a)=8,故a=2. 抽象函數問題常見的還包括證明不等式成立問題,利用其函數基本特征是求解的常規手段,例如形如f(x+y)=f(x)f(y)的抽象函數,可以構建指數函數型[y=ax(a>0,a≠1)]特征函數進行轉化:①確定函數的解析式,即由題設信息分析得到函數的具體形式,例如y=a2等;②判斷函數的單調性,即根據函數解析式和題設條件,猜測函數在對應定義域內的單調性;③利用函數基本特征分析求解,即結合已知條件和函數的基本特征如f(x+y)=f(x)f(y),解得所求值. 例3已知函數f(x)對任意x,y∈R,都滿足f(x+y)=f(x)f(y),且當x>0時,有0 分析:首先結合題意得到y=e-x是函數f(x)的原型,從而猜測f(x)是減函數,再利用指數函數的基本特征f(x+y)=f(x)f(y)分析,得到0 證明 :依題意,得f(1)=f(1+0)=f(1)f(0). 又f(1)>0,所以f(0)=1. 所以f(0)=f[x+(-x)]=f(x)f(-x)=1. 當x<0時,則-x>0,0 故f(x)>1. 綜上所述,當x<0時,f(x)>1. 證明:因為當x>0時,0 f(x2)f(y2)=f(x2+y2)>f(1). 因為函數f(x)在R上單調遞減,所以 x2+y2<1. 故集合A代表圓面x2+y2<1內點的集合. 因為f(1)=f(0+1)=f(0)f(1),且f(1)>0,所以 f(0)=1. 由上述三個案例及其解題思路可以發現,對于有關抽象函數問題,首先需要根據題意構建對應函數類型,然后分析函數單調性,再利用對應的基本特征求解.因此一定要仔細分析題意,并熟悉各類函數的形式和性質,確保求解方向正確.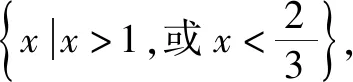

2 f(xy)=f(x)f(y)型
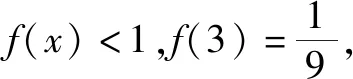
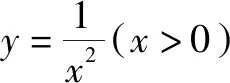
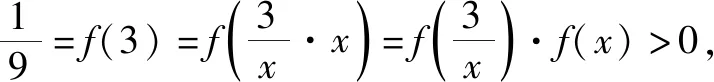
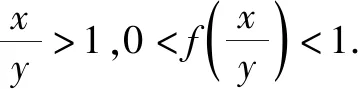
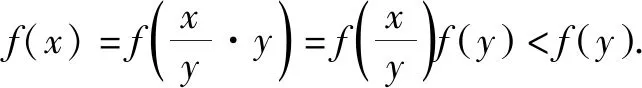
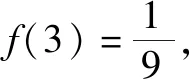
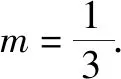
3 f(x+y)=f(x)f(y)型