Caputo 型線性分數階常微分方程的一種新的高階數值方法
2022-12-07 07:52:40朱鵬程
科學技術創新 2022年34期
朱鵬程
(貴州民族大學數據科學與信息工程學院, 貴州 貴陽 550025)
現如今,很多的領域都涉及到了分數階微分方程的應用問題。比如在數學、航天工程、金融、粘彈性材料等領域。并且,它正逐漸成為國內外學者研究的熱點之一。
文獻[1]的作者利用格林函數和不動定理,解決了非線性黎曼- 劉偉爾型分數階方程耦合系統問題。文獻[2]的作者通過證明并使用經典的控制收斂定理直接證明了非線性高階時滯方程解的存在性。文獻[3]的作者研究出了一種變分迭代法用于解決含有某類分數階積分微分方程的問題。文獻[4]的作者構造了一種新穎簡便的正則化方法來逼近分數階導數。在文獻[5]中, 作者通過阿多米安多項式逼近一類非線性分數階積分微分方程中的積分項,從而得到這類問題的數值解。文獻[6]的作者為Caputo 型的分數階常微分方程提供了一個新的平滑度數值解。
本研究的主要研究工作分為三個部分:在第一部分通過分段的三次插值公式近似Caputo 型分數階導數,從而構造了線性分數階常微分方程的高階數值格式。在第二部分對構造的數值格式的截斷局部誤差進行估計。在第三部分我們舉出一個數值算例證明理論分析的正確性。
1 高階數值格式的構造
我們用下面的等式來表示線性分數階常微分方程的高階數值格式:
2 局部截斷誤差估計
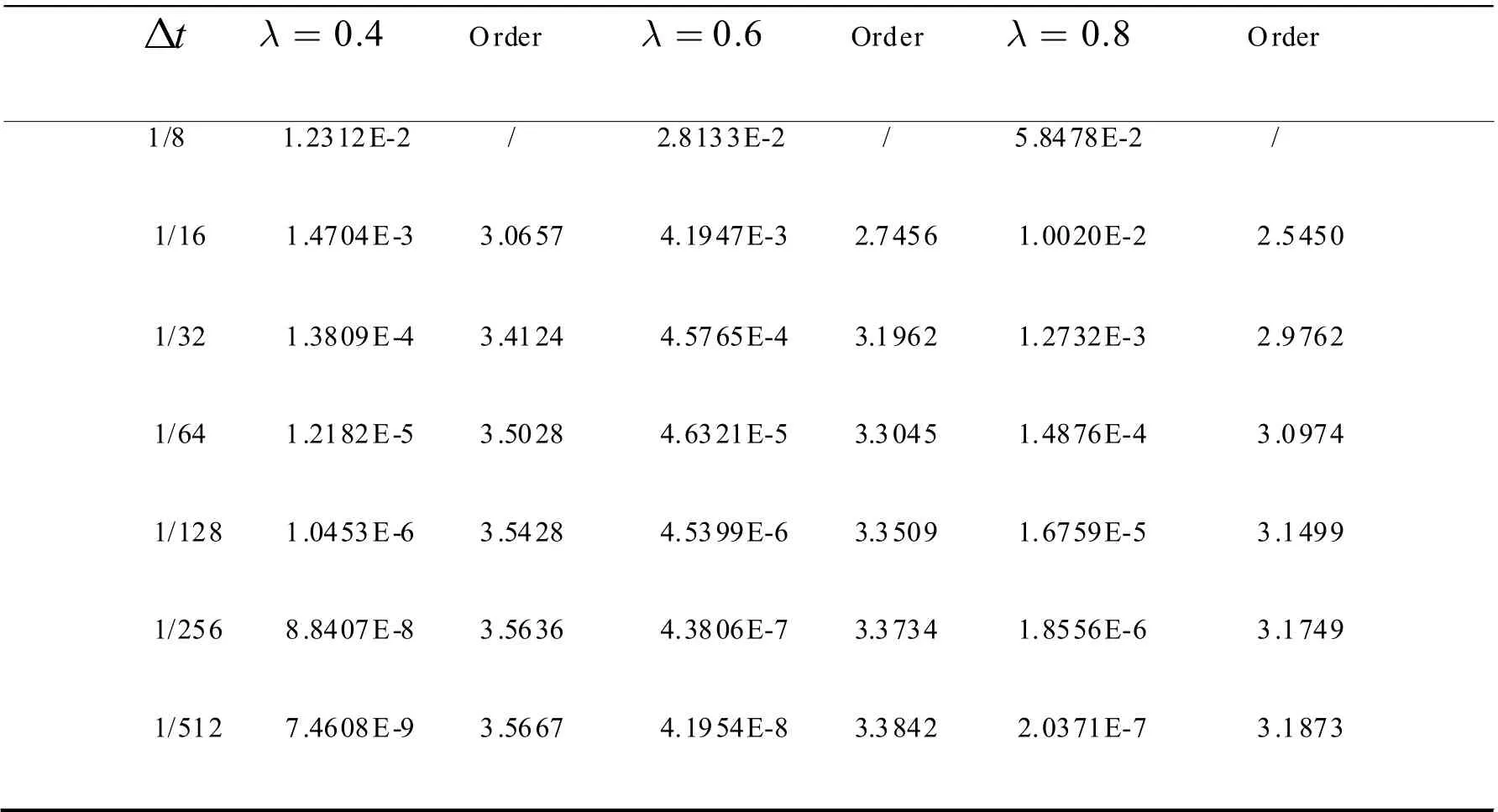
表1 Δt 分別取1/8,1/16,...,1/512 時的最大絕對誤差和收斂階

