面向三自由度平面關節機器人的“S”形軌跡規劃算法研究

陳登錢，孔維賓,2，王德智，孔祥曄，平 欣

(1.鹽城工學院，江蘇 鹽城 224051；2.鹽城工學院光電信息技術研究所，江蘇 鹽城 224051；3.光馳科技(上海)有限公司，上海 200444)

1 引言(Introduction)

隨著機器人技術的迅速發展，智能機器輔助等成為現代機器人技術的研究熱點[1-2]。機器人的使用場合不同，對末端執行器位移、速度等的要求也不盡相同，因此需要對機器人的運行軌跡進行規劃以滿足其穩定性要求。平面關節機器人廣泛應用于汽車等重要行業。關節空間軌跡是針對各關節實時位移角度及連續的運動軌跡，機器人以各關節同時啟停為目標，保證關節同時到達指定位置；而多軸運動插補的總時長取決于運動距離最遠軸，并以關節運動時間為基礎，其余多軸通過改變規劃的最大運動速度與加速度實現時間同步[3-4]。關節空間規劃路徑中無突變點存在，避免規劃中出現瞬時速度過大導致關節運動失控[5-6]。

現有軌跡規劃常用的方式包括五次多項式和“S”形軌跡規劃[7]等。王川等[8]對五次多項式函數插值方法中軌跡中間點角速度的設置方法提出改進。錢文學等[9]提出一種多節點、多樣條曲線運動的軌跡規劃方法。由于關節轉角范圍未確定最優解，同時加加速度軌跡均為不連續曲線，因此在加減速的啟動停止瞬間存在突變現象將會導致系統振蕩，對機械會產生柔性沖擊[10-13]。本文采用雙變量反正切函數規劃機器人的最優關節轉角范圍，利用三角函數結合傳統“S”形軌跡規劃算法，約束運動過程中的最大速度、加速度、加加速度，改善機器人運動過程中由于加加速度非連續軌跡導致的關節驅動力矩的突變，從而保證機器人運動過程的穩定性。

2 運動學模型(Kinematic model)

如圖1所示，平面關節機器人具有3 個自由度，其中2 個旋轉關節，1 個移動關節。為了描述相鄰兩個坐標之間的位置和姿態，采用D-H模型方法建立坐標系，如圖2所示。表1給出了機器人各關節D-H參數。

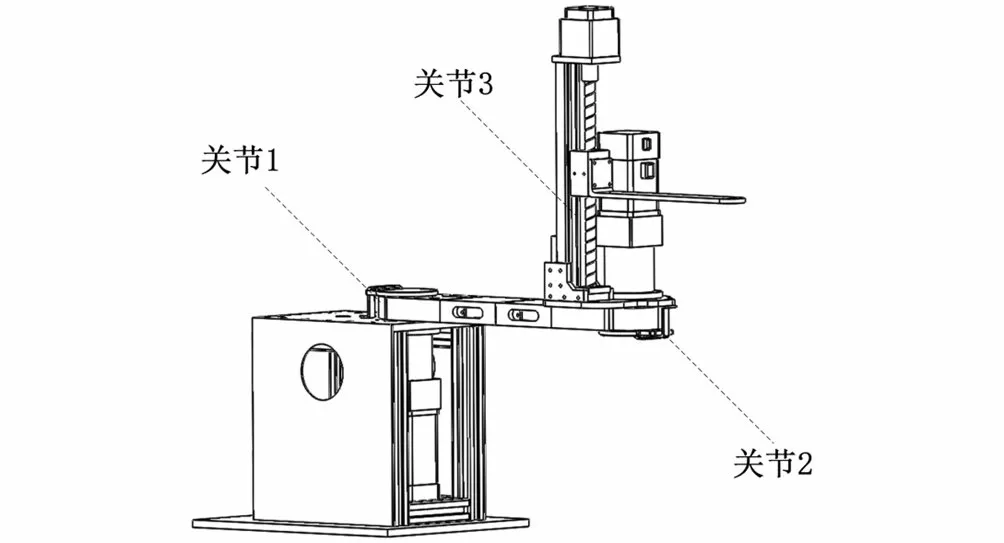
圖1 平面關節機器人結構圖Fig.1 Structural diagram of planar joint robot

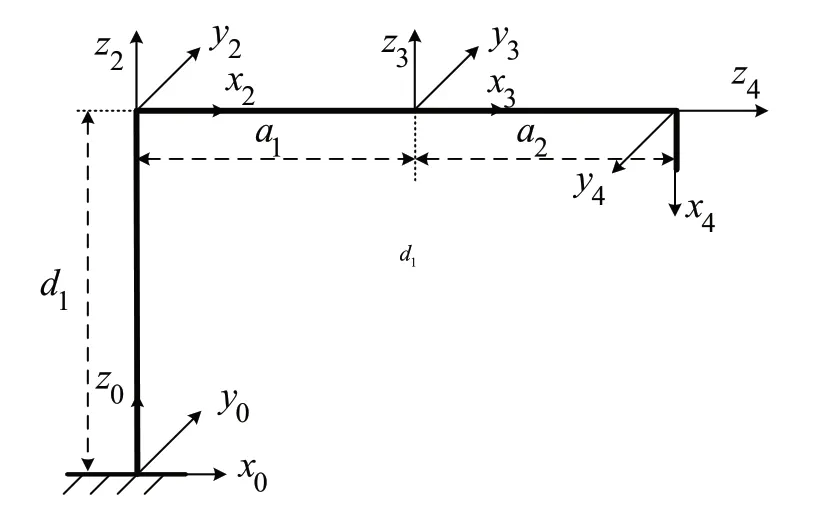
圖2 平面關節機器人D-H模型Fig.2 D-H model of planar joint robot

表1 機器人各關節D-H參數值Tab.1 D-H parameter values of robot joints

以每個關節分別作為坐標原點建立局部坐標系，旋轉矩陣表示關節i相對于關節i-1的位姿矩陣變換，其表達式如下：

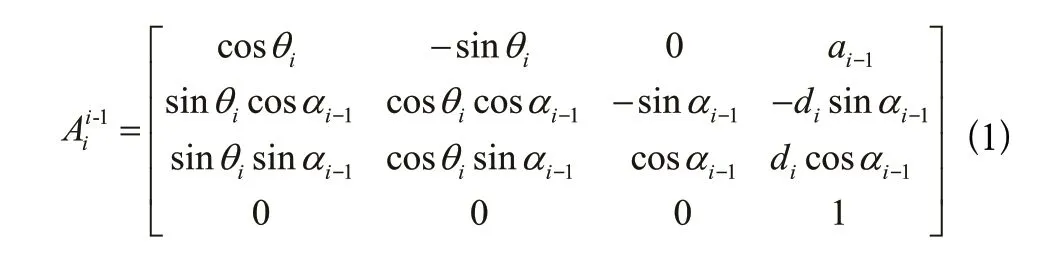
其中，αi-1表示連桿扭角，由于連桿無自轉，所以三關節連桿扭角均為0。表示連桿長度，θi表示關節轉角，di表示關節偏置量。

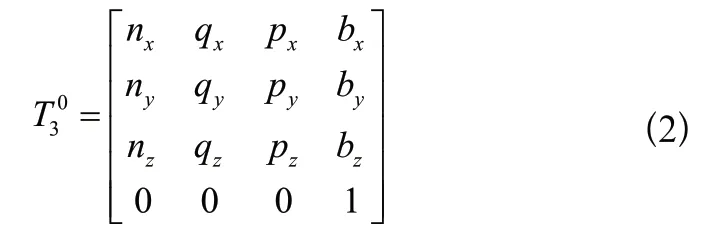
每個關節相對于初始關節坐標系的旋轉變換矩陣可以通過若干個關節的旋轉變換矩陣乘積表示，即機器人末端關節相對于初始關節坐標系的旋轉變換矩陣可以表示為，等式兩邊同乘，可得，從而得到：

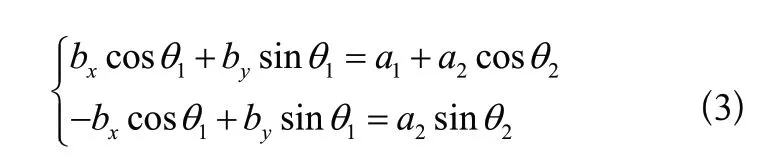
為了有效避免運動學逆解的復雜性及減小逆解的誤差，引入雙變量反正切函數arctan 2(y,x)，反正切函數相比反正弦和反余弦函數主要有以下優點：①確定唯一解，由于雙變量規定了x和y符號，因此能夠確定角度所在象限，所以使其在內具有唯一解，避免出現多解情況。②降低逆解的誤差，保證逆解的精度，函數y=f(x)的計算誤差可以表示為 Δy=Δxf＇(x)。由于f1(x) = arcsinx和f2(x)= arccosx的導數值域范圍內都存在趨向于無窮的值，致使Δy變大，而f3(x)= arctanx的導數值域保持在[0,1)的范圍內，因此可以保證機器人的精度。

依據式(3)可得：

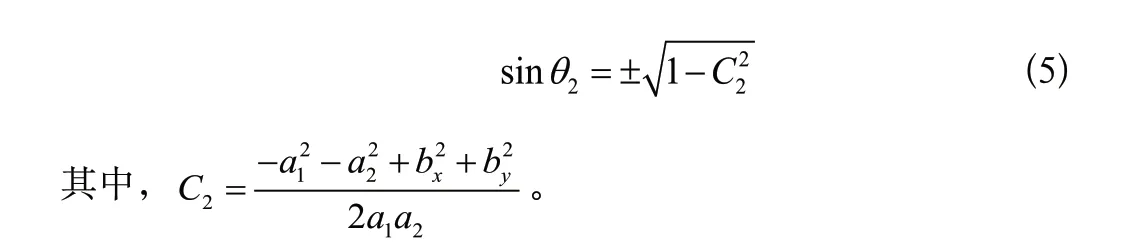
記S2=sinθ2，由式(3)、式(4)和式(5)可得平面關節機器人關節1、2的轉角θ i與關節3的偏移量d3：

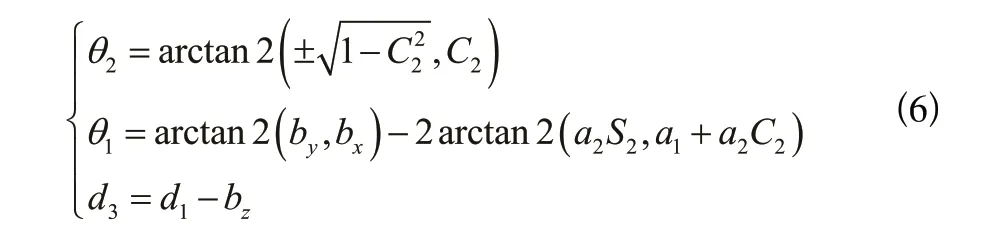
當確定機器人末端位姿矩陣時，對于θ2與θ1，關節1與關節2都有兩個解，分別對應每個關節電機的正反旋轉，因此機器人進行路徑規劃時，需要對多組解進行最優化選解，使機器人的運動處于最佳狀態。如圖3所示，由機器人運動準則可得最優選解過程。

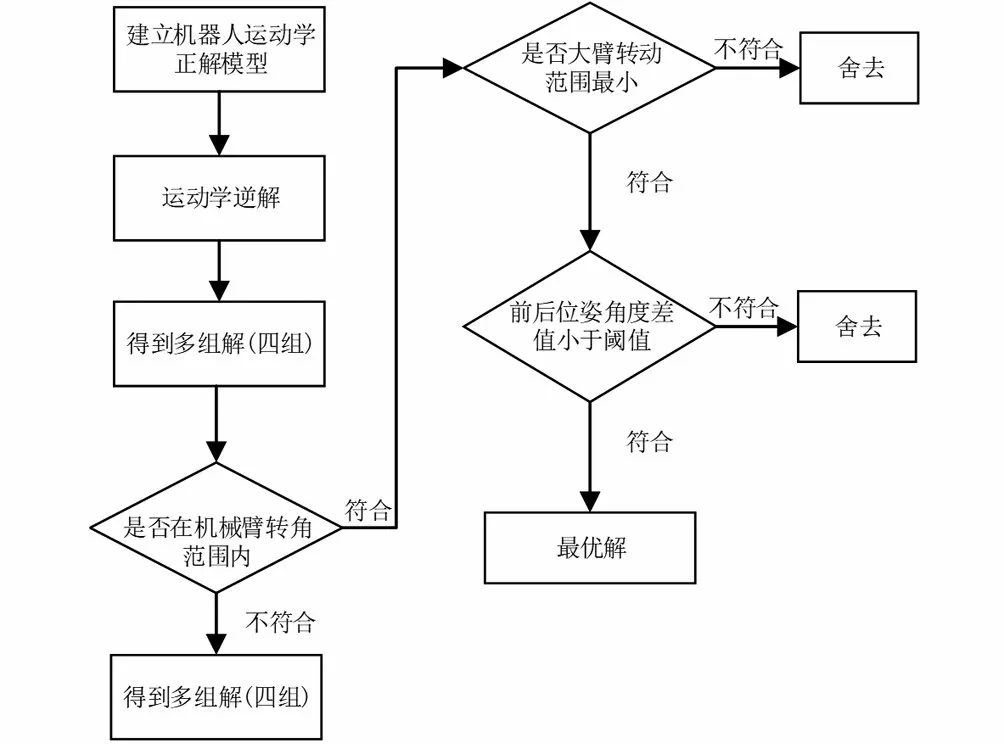
圖3 機器人最優選解流程圖Fig.3 Flow chart of robot optimal selection

使用Matlab Robotic工具箱對機器人末端進行仿真，將機器人末端從初始坐標點運動到目標點。如表2所示，第二組解中，關節1轉角，超出關節1的轉角允許范圍。第二組解中，關節1的轉角大于第一組解關節1的轉角，依據機器人最優選解準則，選擇第一組解作為完成該運動的最優逆解。依據最優逆解，機器人末端運動軌跡及各關節運動曲線圖，如圖4所示，關節1的位移量與速度比關節2小，并且各關節的運動均勻平穩，速度及位移沒有出現突變現象，符合機器人運動的柔順性要求。

表2 平面關節機器人末端運動逆解Tab.2 Inverse solution of end motion of planar joint robot

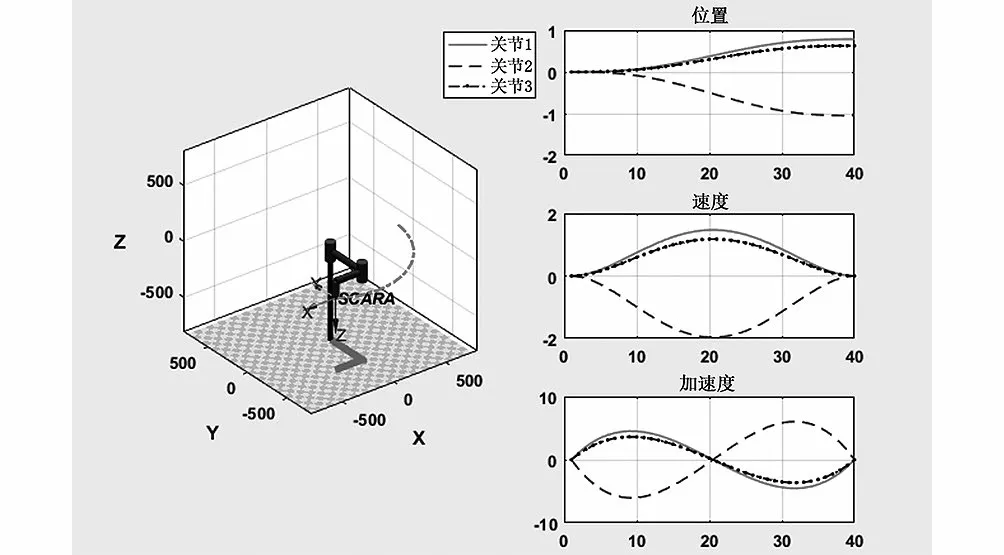
圖4 機器人各關節運動曲線圖Fig.4 Motion curve of each robot joint

3 關節空間軌跡規劃(Joint space trajectory planning)

3.1 改進“S”形軌跡規劃

如圖5所示，將“S”形軌跡分為加加速段[0,t1]、勻加速段 [t1,t2]、減加速度 [t2,t3]、勻速段 [t3,t4]、加減速段 [t4,t5]、勻減速段 [t5,t6]、減減速段 [t6,t7]七段。軌跡規劃的輸入參數包括機器人系統機械性能約束量最大速度Vm、最大加速度Am、最大加加速度Jm及目標軌跡約束的各關節運動位移Qi。假設三個關節中最大位移為Qm，并以該位移規劃整體軌跡運行時間，將各關節速度、加速度、加加速度的始、末數值均為0設置為初始條件。

圖5 改進“S”形規劃軌跡Fig.5 Improved S-shaped trajectory planning

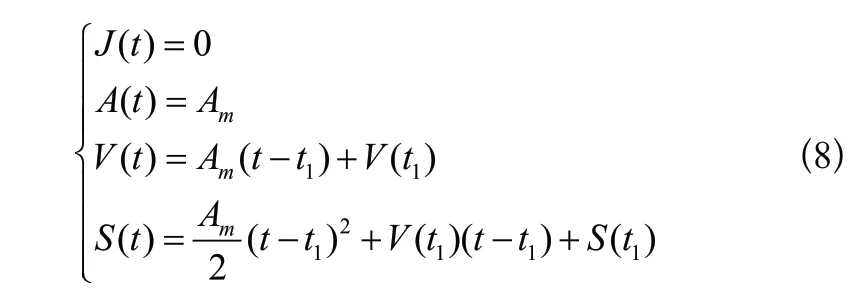
(3)減加速段t∈[t2,t3]。該段軌跡初始加加速度J(t2)為0，加速度為Am，結束時加加速度J(t3)為0，加速度A(t3)減為0，速度達到Vm，根據以上條件可以得到該段時間內的軌跡，即

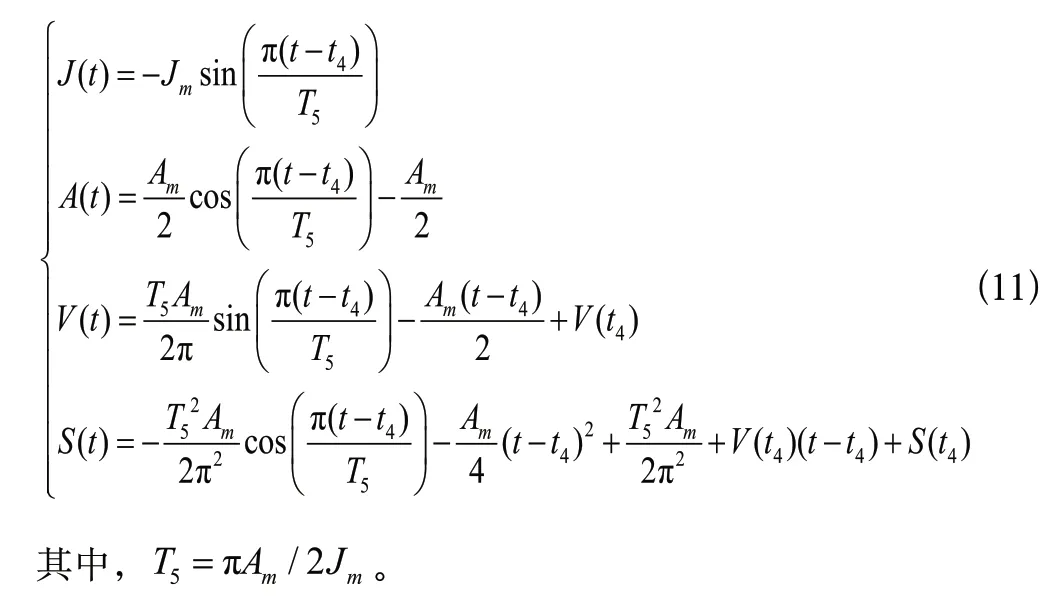
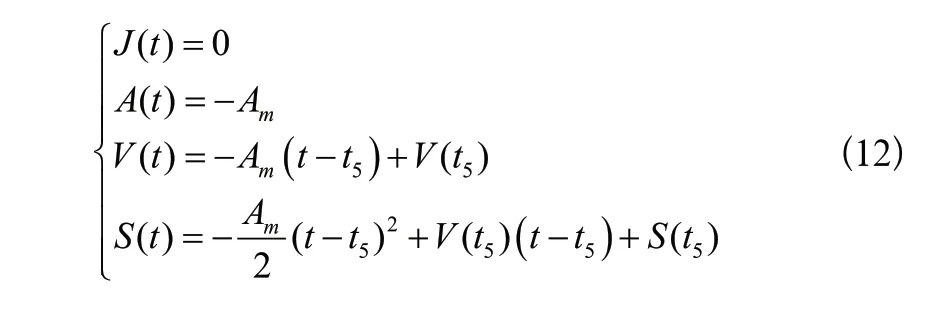
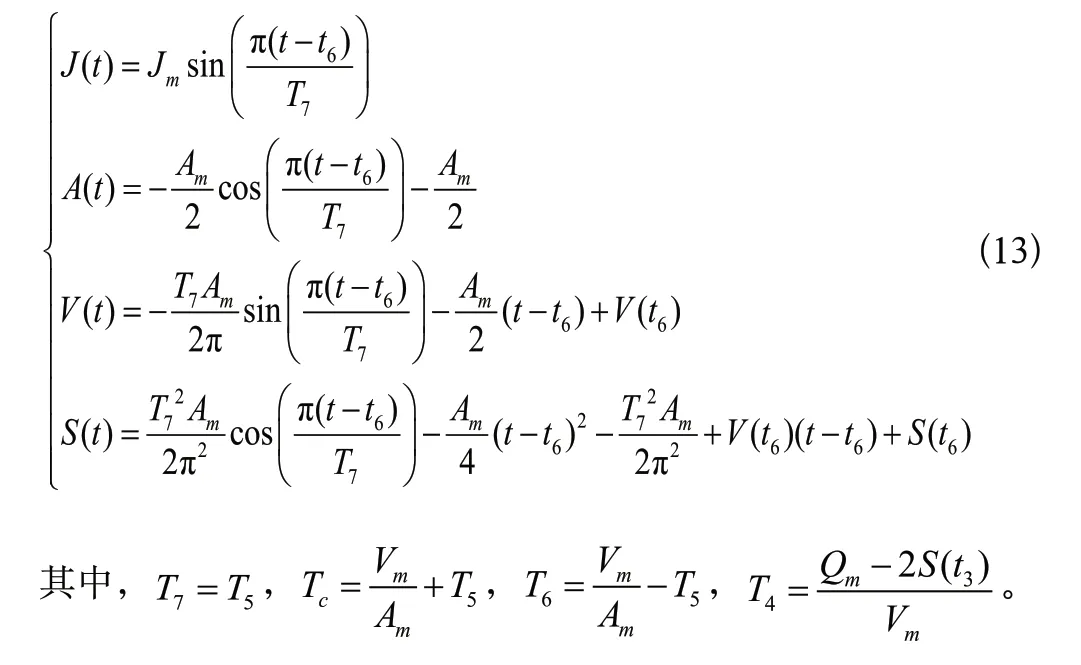
3.2 關節軌跡規劃流程

根據目標軌跡約束條件，勻加速、勻速、勻減速部分時間長度，即T2、T4、T6為0，軌跡規劃步驟如圖6所示。

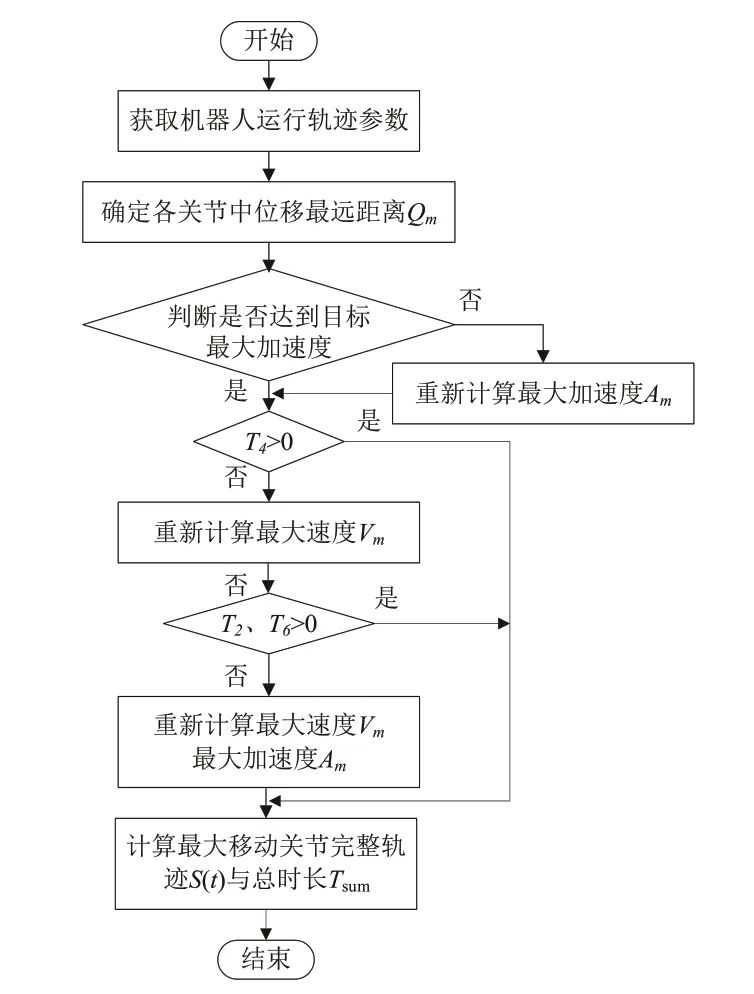
圖6 關節軌跡規劃流程圖Fig.6 Flow chart of joint trajectory planning

步驟1：獲取機器人運行軌跡參數，包括各關節當前位置P1、目標位置P2、最大速度Vm、最大加速度Am、最大加加速度Jm，判斷位移距離最遠關節的運動范圍

步驟2：根據設定的最大速度與加加速度計算是否能達到目標最大加速度，如果，則調整最大加速度約束量，即

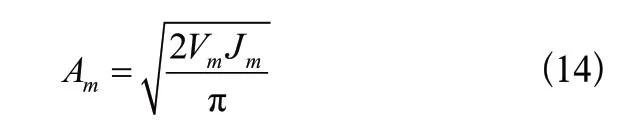
步驟3：判斷軌跡中是否存在勻速段，即計算T4>0是否成立，若成立則規劃軌跡為完整軌跡，跳轉到步驟7。

步驟4：若T4>0不成立，即軌跡無勻速段，最大速度不可達，調整最大速度約束量，其條件為T4=0且S(t7) =Qm，即

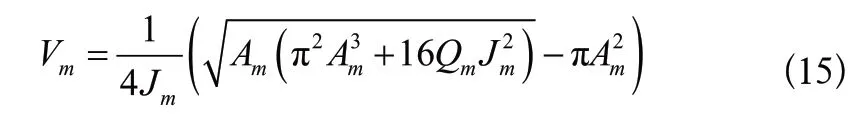
步驟5：判斷是否存在勻加勻減速段，即計算T2>0，T6>0是否成立，若成立，則跳轉到步驟7。

步驟6：若T2>0，T6>0不成立，即軌跡無勻加減速段，最大加速度不可達，調整最大速度與最大加速度的約束量，根據條件T2=0、T4=0、T6=0且S(t7) =Qm，可得

步驟7：根據上述所得最終最大速度與加速度，可以得到最大移動關節的完整軌跡、各段軌跡時間長度T(i)及總時長。

4 實驗分析(Experimental analysis)

為驗證所提出連續有界的多關節改進“S”形時間同步軌跡規劃算法，設置平面關節機器人運動路徑起始點P1及終止點P2，采集并分析機械臂第一關節期望軌跡與實際反饋的關節運動軌跡。圖7(a)的A、B兩點表示機器人換向運動階段，此時機器人關節經歷減速、靜止、加速三個階段，由于慣性力和減速器背隙的存在，因此會出現較大的誤差波動。如圖7(b)、圖7(c)所示，傳統“S”形軌跡算法出現了較大的誤差波動，而改進“S”形軌跡算法的誤差變化較為穩定。由此可知，本文所提出的加加速度連續有界的多關節改進“S”形時間同步軌跡規劃方法能夠正確規劃出不同約束條件下的目標軌跡，該方法適用于平面關節機器人連續有界平滑軌跡規劃，利用改進“S”形軌跡實現速度、加速度和加加速度有界的連續軌跡規劃，避免階躍與沖擊，并且保證規劃的最大速度、加速度、加加速度均不超過系統設定的最大限制量。

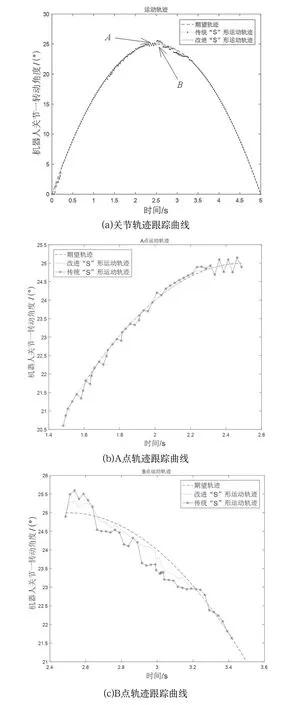
圖7 平面關節機器人第一關節軌跡跟蹤曲線Fig.7 Trajectory tracking curve of the first joint of planar joint robot

5 結論(Conclusion)

本文通過引入雙變量反正切函數結合運動學逆解的方法規劃機器人最優關節轉角范圍，利用三角函數改進“S”形軌跡規劃算法，約束運動過程中的最大速度、加速度、加加速度的限制值，改善了機器人運動過程中由于加加速度非連續軌跡導致關節驅動力矩的突變。相較于傳統算法，改進的“S”形軌跡規劃算法有效提升了機器人的穩定性，改善了機器人的運動軌跡突變情況。