基于特征曲線法的圍巖-支護系統安全性分析

趙昌杰，饒軍應，熊 鵬，王亞奇，陳 憶

(1.貴州大學土木工程學院，貴州 貴陽 550025；2.貴州大學空間結構研究中心，貴州 貴陽 550025)

1 概述

近年來高速公路、高速鐵路等系統交通工程的建設日新月異，隧道工程亦隨之迅速發展。尤其在西南山區，高速公路及高鐵的隧道占比高，埋深大，所處地質較復雜，支護結構設計困難。以往的隧道穩定性分析及支護結構設計方法包括數值法[1- 2]、經驗法[3- 4]和解析法[5- 9]等，但通常依靠經驗類比，不能充分反映圍巖及支護結構的平衡關系。而特征曲線法[10- 14]視圍巖為主要的承載單元，充分考慮了圍巖-支護系統的相互作用，支護的本質作用是“調動圍巖承載”和“協助圍巖承載”[15]。特征曲線法是國際隧道協會(ITA)歸納的4種隧道結構設計模型之一[16]，廣泛應用于新奧法，其核心思想是將圍巖視作隧道的主要承載單元，隧道開挖時允許圍巖有一定的變形量，使之在隧道周圍形成承載環，但又采取薄層支護手段對變形嚴格控制，避免隧道變形過大而失穩。該方法是通過圍巖特征曲線和支護特征曲線的交匯確定隧道支護體系的平衡點，圍巖和支護結構是其中2個關鍵的因素，它們的相互作用機理對圍巖穩定性的分析有重要的作用。

唐雄俊[17]最早提出了特征曲線法思想，Fairhurst[18]亦應用彈塑性原理，指出了圍巖特征曲線是一條隨著初始地應力逐漸釋放，圍巖變形逐漸增大的曲線。之后，Bernaud[19]驗證了特征曲線法在深埋隧道中的適用性。在理論方面，張常光等[20]基于統一強度理論和非關聯流動法則，推導了深埋圓形巖石隧道圍巖特征曲線解析新解；蘇永華等[21]基于并聯體系原理，導出了組合支護結構特征函數，并結合收斂-約束原理構建了支護結構穩定性系數計算方法；晏勤[22]考慮錨桿對圍巖的加固效應，通過均勻化方法，推導了錨桿加固作用下的圓形隧道復合巖體圍巖特征曲線解析解。在圍巖特征曲線影響因素方面，金豐年[23]考慮了時間效應對圍巖特征曲線的影響；張素敏等[16]選擇彈塑性有限元方法，作出了各種圍巖級別和不同埋深下的單、雙線毛洞的圍巖特征曲線。在支護時機和支護剛度選擇方面，陳峰賓[24]給出了考慮噴射混凝土硬化的軟巖隧道支護時機的確定方法和初期支護安全性能評價方法；張子龍等[25]提出了基于收斂約束原理和圍巖局部安全評價方法單元狀態指標的初期支護時機確定方法。

本文基于彈塑性原理，推導了深埋隧道圍巖位移計算理論，闡述了圍巖特征曲線(Ground Response Curve，GRC)與支護特征曲線(Support Characteristic Curve，SCC)及縱向變形曲線(Longitudinal Deformation Profile，LDP)的對應關系，并引入圍巖穩定安全系數、支護結構安全系數和圍巖變形控制率對支護起點和支護剛度的選擇進行綜合評價，進而定性分析了圍巖級別、隧道埋深和隧道洞徑對圍巖特征曲線的影響，最后利用該理論對實際工程案例進行應用、指導。

2 圍巖力學特性

2.1 圍巖應力狀態與破壞

當硐室開挖后，巖體出現臨空面，隨著應力局部釋放，圍巖向洞內發生擠入變形。由于變形，初始應力場狀態發生應力的重分布，即二次應力場。對于彈塑性巖體，其應力-應變關系呈非線性，當洞周切應力滿足巖體屈服條件時，圍巖即進入塑性狀態，塑性區使應力向圍巖深部不斷延伸。隧道硐室不加以支護，隨著圍巖應力和強度的降低，即出現松動區，此時圍巖裂隙不斷發展，松動區不斷增大，圍巖出現塑性滑移，硐室即將發生失穩破壞。彈塑性巖體中的應力圖形如圖1所示：

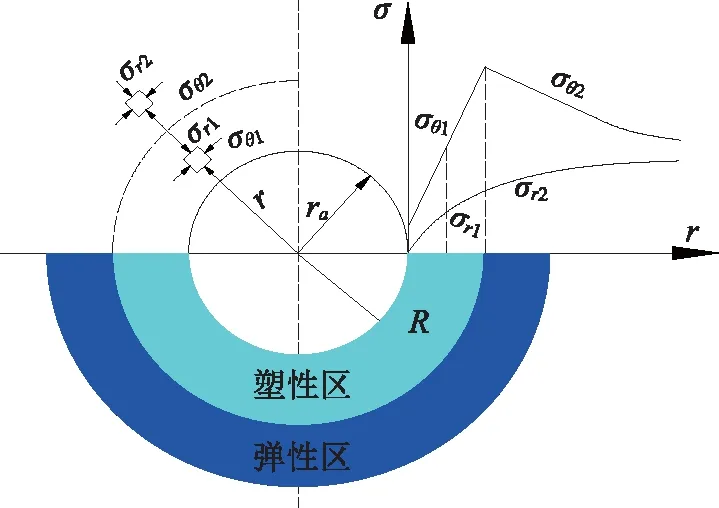
圖1 圍巖應力狀態分布圖

2.2 圍巖塑性判據

圓形隧道開挖問題計算模型如圖2所示，圍巖初始應力場為：

σz=γh，σx=λγh

(1)

式中，σz—自重應力場下的豎直應力，MPa；σx—自重應力場下的水平應力，MPa；λ—側壓力系數；γ—圍巖容重，kN/m3；h—隧道埋深，m。

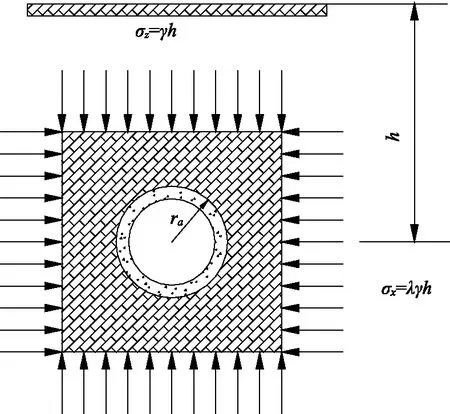
圖2 圓形隧道開挖問題計算模型

在彈塑性分析中，常選用Mohr-Column條件作為塑性判據，亦稱屈服準則[26]。式(2)便是現在常采用的硐室圍巖塑性區的塑性判據。

σθ1-ξσr1-Sc=0

(2)

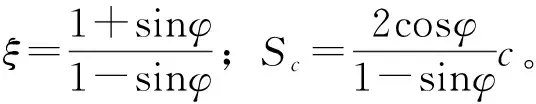
本文研究的是側壓力系數λ=1的軸對稱隧道問題。此時，硐室周邊的σθ=2σz，σr=0。將此式帶入式(2)得：

2σz-Sc=0

(3)

使σz=γh，即得軸對稱隧道壁圍巖進入塑性狀態的判別式：

2γh≥Sc

(4)

2.3 圍巖彈塑性分析

2.3.1塑性區的應力場

取塑性區內的任意一點進行分析，其需滿足平衡方程，在λ=1的條件下，其極坐標平衡方程為：

(5)

另還需滿足屈服條件，由(2)式得：

將σθ1代入(5)式計算得：

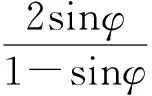
(6)

此時考慮支護阻力Pa的作用，即在r=ra時，σr1=Pa，得積分常數：

代入(5)、(6)式得：

將Sc、ξ代入得：

(7)

2.3.2彈性區的應力場位移場

當塑性區過渡到彈性區，其應力狀態僅受原巖應力狀態和塑性區邊界應力的影響。彈性的應力解答仍屬于無限彈性平面內的孔口問題，只需注意邊界條件有所差別：

在無限遠處(r=∞)有：σr2=γh。

在r=R處有：

σr2=σr1=σR，σθ2=σθ1

(8)

對于軸對稱問題(λ=1)，圍巖應力在彈性力學里有現成的G.Lame公式解答[22]：

(9)

(10)

式中，G—圍巖的剪切模量，GPa；v—圍巖切向位移，m。

在r>R處，考慮為作用有支護阻力Pa=σR，可得彈性區應力、位移解答：

(11)

(12)

當r=ra時，即得隧道洞周彈性圍巖解答：

(13)

2.3.3塑性區半徑

彈塑性邊界面上的應力既應滿足塑性條件，又應滿足彈性條件，將(11)式中的2式相加，消去σR，即得彈塑性邊界上應力彈性條件為：

σr2+σθ2=2σz

(14)

結合(8)式，即得彈塑性邊界上應力塑性條件：

σr1+σθ1=2σz

(15)

將式(2)、(14)和(15)聯立求解，即可解出在r=R處的應力：

(16)

將r=R代入式(7)，并聯立式(16)，即可求出塑性區半徑顯示表達式：

(17)

當R=ra時，即表示圍巖出現塑性區的臨界點，將R=ra代入(17)式得不形成塑性區時所需的支護阻力：

Pa0=σz(1-sinφ)-c·cosφ

(18)

始終，Pa0為不形成塑性區所需的支護阻力。

2.3.4塑性區的位移場

假定圍巖塑性區內的巖體在小變形的情況下體積不變，得：

εr1+εθ1+εz1=0

(19)

結合平面應變狀態下的幾何方程得：

代入式(19)得：

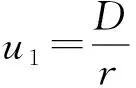
式中，D—待定系數，可由彈塑性邊界上的位移協調條件ur1=ur2，并聯立ur1、ur2解得塑性區位移表達式為：

(20)

將R代入ur1，并令r=ra即可解出隧道壁徑向位移ura與支護阻力Pa的關系式，即圍巖特征曲線函數(GRC)：

(21)

因式(21)的適用對象為圓形斷面隧道，對于非圓形隧道斷面，本文選用“當量半徑法”[27]進行轉化。即假想存在一個虛擬圓，其面積等于實際非圓形隧道斷面面積，其當量半徑為：

(22)

式中，RD—當量半徑，m；S—非圓形隧道斷面面積，m2；f—斷面形狀修正系數，取值見表1：

表1 地下洞室斷面形狀修正系數[27]

3 支護特征曲線

3.1 噴射混凝土

采用下式[24]計算噴射混凝土支護剛度Kc(N/m)：

(23)

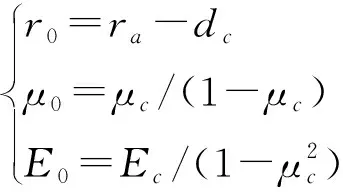
式中，Ec—噴射混凝土彈性模量；μc—噴射混凝土泊松比;dc—噴射混凝土厚度。

噴射混凝土的最大支護阻力為：

(24)

式中，Jc—噴射混凝土抗壓強度。

噴射混凝土允許的極限變形量為：

ulim，c=Pmax，c/Kc

(25)

3.2 錨桿

錨桿的受力條件比較復雜，常采用以下近似公式[28]確定其受拉剛度Kb：

(26)

式中，db—錨桿的直徑；l—錨桿長度；fx—錨桿的橫向間距；fy—錨桿的縱向間距；η—錨固端和錨固頭的荷載變形常數。錨桿最大承載力(Pmax，b)采用下式：

(27)

式中，Qbf—錨桿抗拔試驗破壞荷載。

錨桿允許的極限變形量為：

ulim，b=Pmax，b/Kb

(28)

3.3 鋼拱架

鋼拱架剛度Ks采用Oreste[29]提出的理論公式：

(29)

式中，Es—鋼拱架彈性模量；Ws—各鋼拱架橫截面面積；fs—鋼拱架縱向間距；hs—鋼拱架橫截面高度。

鋼拱架最大承載力Pmax，s采用下式：

(30)

式中，σs—鋼拱架的屈服強度。

錨桿允許的極限變形量為：

ulim，s=Pmax，s/Ks

(31)

3.4 組合支護結構

Carranza-Torresa[30]認為組合支護結構的組合剛度K等于各支護單元剛度Ki之和：

(32)

假定圍巖和支護結構緊密接觸，圍巖對支護結構的反力也是徑向分布的，組合支護結構與其徑向支護阻力可采用以下表達式：

Pmax=Kumin

(33)

式中，Pmax—組合支護結構最大支護力；umin—組合支護結構允許徑向位移，取各支護單元中最小極限位移，即umin=min{ulim，c，ulim，b，ulim，s}。

由上述成果可得SCC的函數表達式：

Pz=K(u-u0)

(34)

式中，Pz—組合支護結構支護力；u—隧道徑向位移；u0—支護起點處隧道徑向位移。

3.5 合理支護起點和支護剛度評價方法

GRC和SCC的關系如圖3所示。初期支護施作起點(u0)和剛度(K)影響著圍巖和支護結構的平衡效果(E點)，本文引入圍巖位移安全系數(Q1)、支護結構安全系數(Q2)和圍巖變形控制率(Ψ)對合理支護起點和支護剛度進行綜合評價。

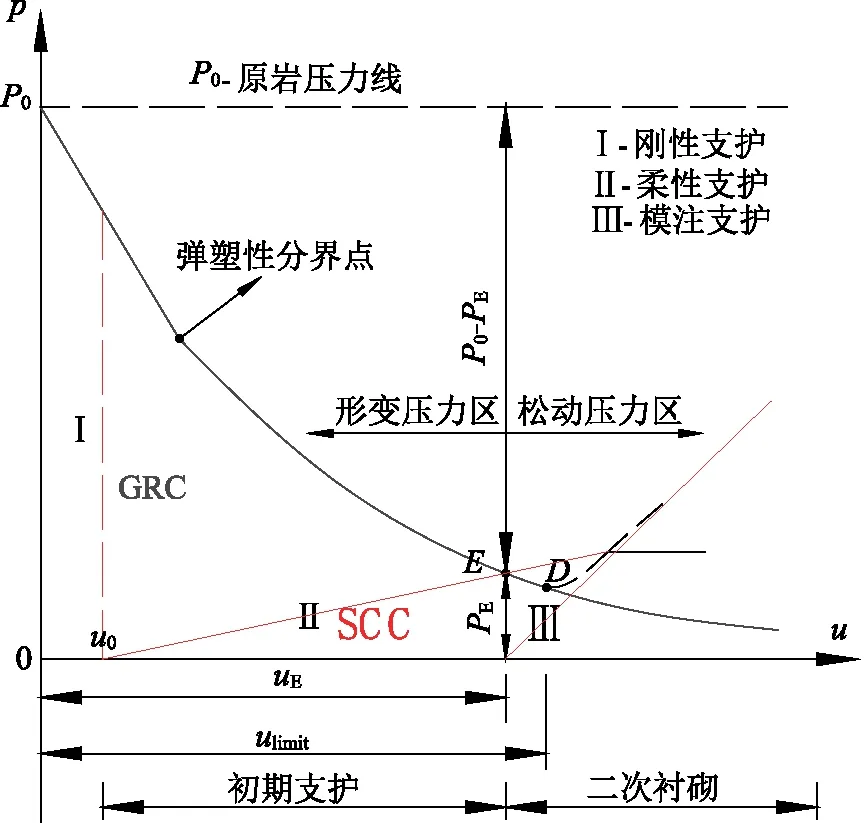
圖3 圍巖與支護結構的相互作用關系

3.5.1圍巖穩定安全系數

隧道圍巖支護系統是一個復雜的綜合體，有眾多因素對隧道支護安全性產生影響，其中圍巖力學狀態尤為重要。而實際施工中，圍巖的性質和狀態均不易監測，但圍巖及支護系統的位移量可反映出圍巖位移狀態，位移量監測簡單易行。故選用基于圍巖位移量的安全性評價方法[24]。

(35)

式中，Q1—圍巖穩定安全系數；ulim—隧道周邊圍巖允許最大位移量(D點位移值)；ueq—初期支護與圍巖變形平衡時圍巖位移值；u0—初期支護開始支護時圍巖位移。

3.5.2支護系統安全系數[21]

(36)

式中，Q2—圍巖穩定安全系數；Peq—初期支護與圍巖變形平衡時的支護力。

3.5.3變形控制率

引用變形控制率[31](Ψ)來反映初期支護的支護效果，Ψ越大，表示支護結構對于圍巖的變形控制效果越好：

(37)

式中，Ψ—初期支護結構對圍巖的變形控制率；ulim—無支護時圍巖發生的最大位移；ueq—施作初期支護后，圍巖最終的穩定位移。

4 縱向變形曲線

Vlachopoulos[32]對滿足彈塑性模型的圍巖，建立了以最大塑性區半徑Rmax為基礎的隧道縱向變形曲線：

(38)

式中,l—隧道斷面至掌子面的距離；Rmax—最大塑性區半徑；u*—掌子面處的位移釋放系數；umax—隧道圍巖無支護狀態下的最大位移。

利用GRC、SCC和LDP進行初期支護結構設計的步驟：

(1)結合式(13)、(18)和(21)，利用Matlab等軟件繪制出GRC；

(2)利用式(17)得到Rmax，再將Rmax、l代入式(38)，得到u0；

(3)利用式(33)繪制出剛度為K的SCC；

(4)通過式(35)—(37)求得Q1、Q2和Ψ。若Q1、Q2大于1，則說明圍巖處于穩定狀態，且支護系統有一定的安全儲備，設計合理；若Q1、Q2小于1，則說明在圍巖支護系統會發生破壞，需要對l及K進行調整，重復步驟b～d，直至Q1、Q2和Ψ取得最優值。

GRC、SCC和LDP的對應關系如圖4所示。

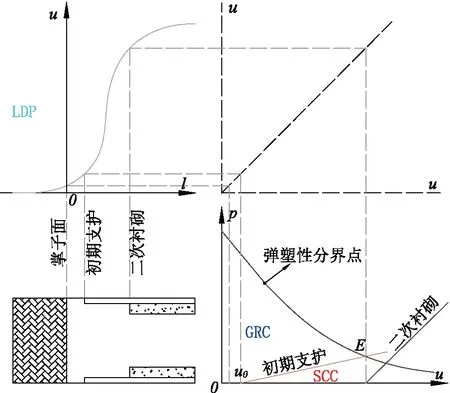
圖4 GRC、SCC和LDP關系圖

5 參數分析

為定性探明圍巖級別、隧道埋深和隧道洞徑對圍巖特征曲線的影響，現取3種工況進行分析，見表2。圍巖級別參數均取自2018版公路隧道設計規范[33]。

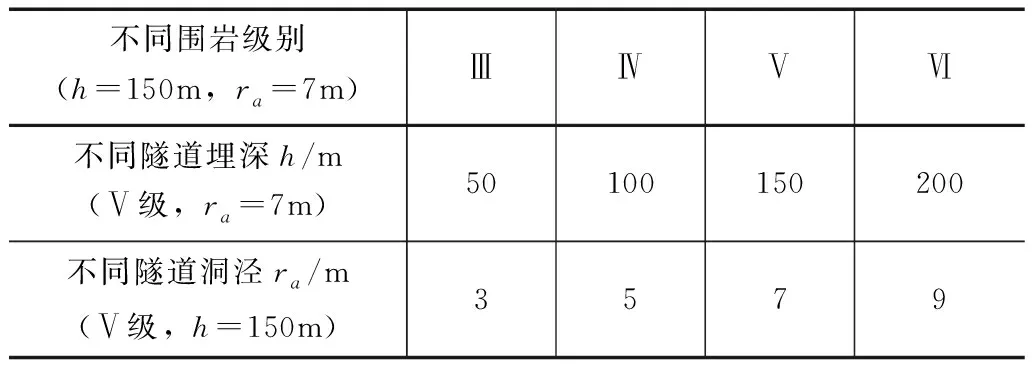
表2 不同工況參數表

5.1 不同圍巖級別對GRC的影響

不同圍巖級別下的GRC對比如圖5所示。由圖5可知，該工況下，整體上圍巖級別越高，隧道圍巖初始應力越低，但隨著位移的逐漸釋放，所需支護力隨之增大。這是因為：圍巖級別越高，其主要工程地質特征、巖石堅硬程度、巖體完整程度等巖性特征均越差；在原始應力狀態時，巖性差的地層應力得到了一定釋放，導致其初始應力較低，但圍巖位移逐漸釋放之后，此類圍巖所能提供的自承載能力越差，需要及時提供足夠剛度和極限承載能力的支護結構予以支撐。從圖5還可以看出，對于巖性特征較好的Ⅲ級圍巖，其最大位移為7.6mm，處于允許極限位移規范值[34]以內(此處為14mm)，表示在該工況下無需施作支護，圍巖依靠自承載能力即能達到自穩。

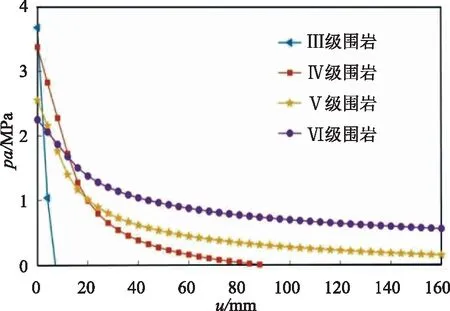
圖5 不同圍巖級別下的GRC對比圖

5.2 不同隧道埋深對GRC的影響

不同隧道埋深下的GRC對比如圖6所示。該工況下，選擇的是Ⅴ級圍巖，巖性較差。由圖6可知，隧道埋深對圍巖特征曲線的影響比較明顯。隨著隧道埋深的增加，表現為初始地應力愈大。在埋深較大的情況下，圍巖的塑性變形愈大，其彈性變形所占比例愈小，此時若要維持隧道圍巖在彈性階段，需要提供較大剛度和約束壓力。但若允許圍巖發生一定位移釋放后，其圍巖自身塑性變形所承擔的圍巖壓力增大，同時所需的支護壓力明顯減小。在此類圍巖中施作柔性支護的重要原因，就是依靠柔性支護既能使圍巖變形得到有效控制，又能使圍巖位移得到一定釋放，充分

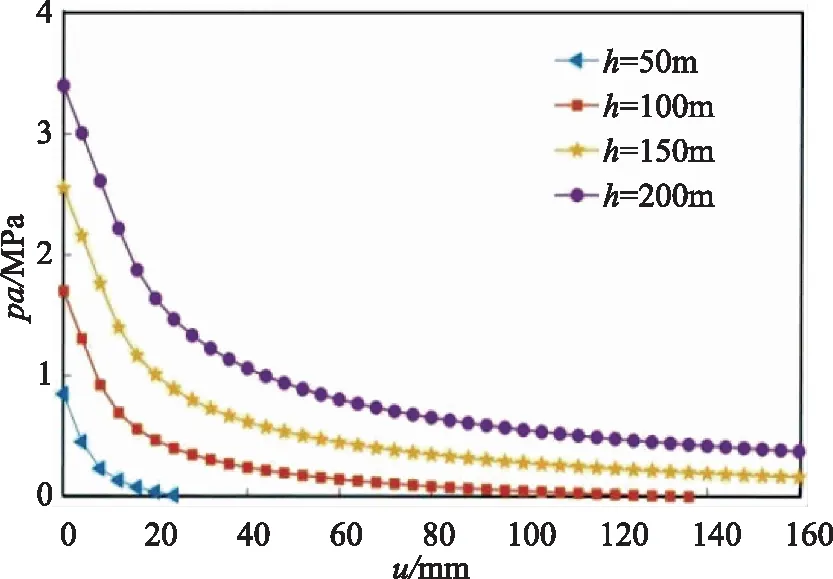
圖6 不同隧道埋深下的GRC對比圖

發揮圍巖自身的承載能力，更好地調節巖體和支護結構的應力、應變狀態，最大化減小支護結構所需提供的阻力。

5.3 不同隧道洞徑對GRC的影響

不同隧道洞徑下的GRC對比如圖7所示。由圖7可知，該工況下，圍巖初始應力均相同，但隨著隧道洞徑的增大，其圍巖塑性變形逐漸增大。這是因為：由式(17)可知，洞徑愈大，圍巖塑性區半徑愈大，對地層的影響范圍愈廣。

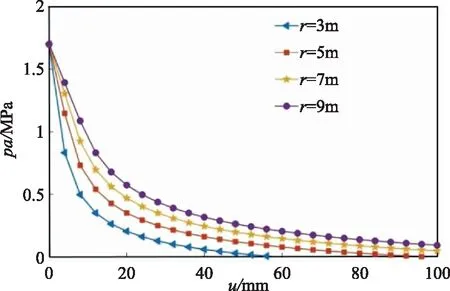
圖7 不同隧道洞徑下的GRC對比圖

6 典例分析

昭通至瀘州高速公路彝良至鎮雄段白巖腳隧道，隧道全長左幅5265m，右幅5245m，最大埋深470m。隧道區地形較為陡峻，屬構造侵蝕中山地貌區，圍巖以強風化白云巖為主，部分為中分化。選取典型里程段左幅ZK20+860～ZK21+000段和ZK25+200～ZK25+300段進行隧道初期支護設計驗證，左幅地質縱斷面如圖8所示。根據地質勘探資料，ZK20+860～ZK21+000段為Ⅴ1圍巖，最大埋深190m，支護結構橫斷面如圖10所示；ZK25+200～ZK25+300段為Ⅳ1圍巖，最大埋深200m，支護結構橫斷面如圖9所示。根據公路隧道設計規范，Ⅴ1圍巖和Ⅳ1圍巖均取規范值[33]，其物理參數如表3所示。有學者認為[34]，基于彈塑性原理分析下的隧道圍巖位移偏于保守，故隧道周邊允許相對位移值依據規范[35]，并結合巖性特征，Ⅳ1圍巖允許相對位移值按Ⅲ級圍巖取為0.2%；Ⅴ1圍巖按Ⅳ級圍巖取為0.4%。因Ⅳ圍巖斷面隧道寬12m，Ⅴ圍巖寬12.5m，故隧道周邊極限位移值Ⅳ圍巖為24mm，Ⅴ圍巖為50mm。

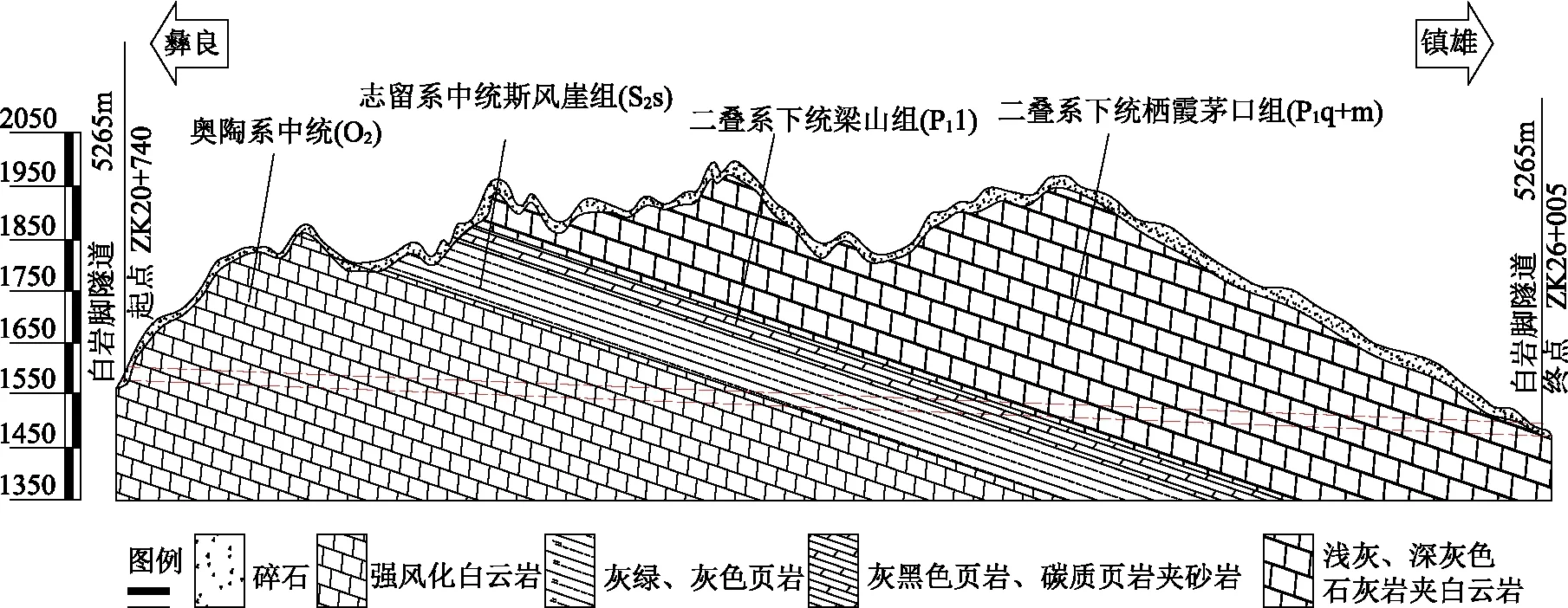
圖8 白巖腳隧道左線地質縱斷面示意圖

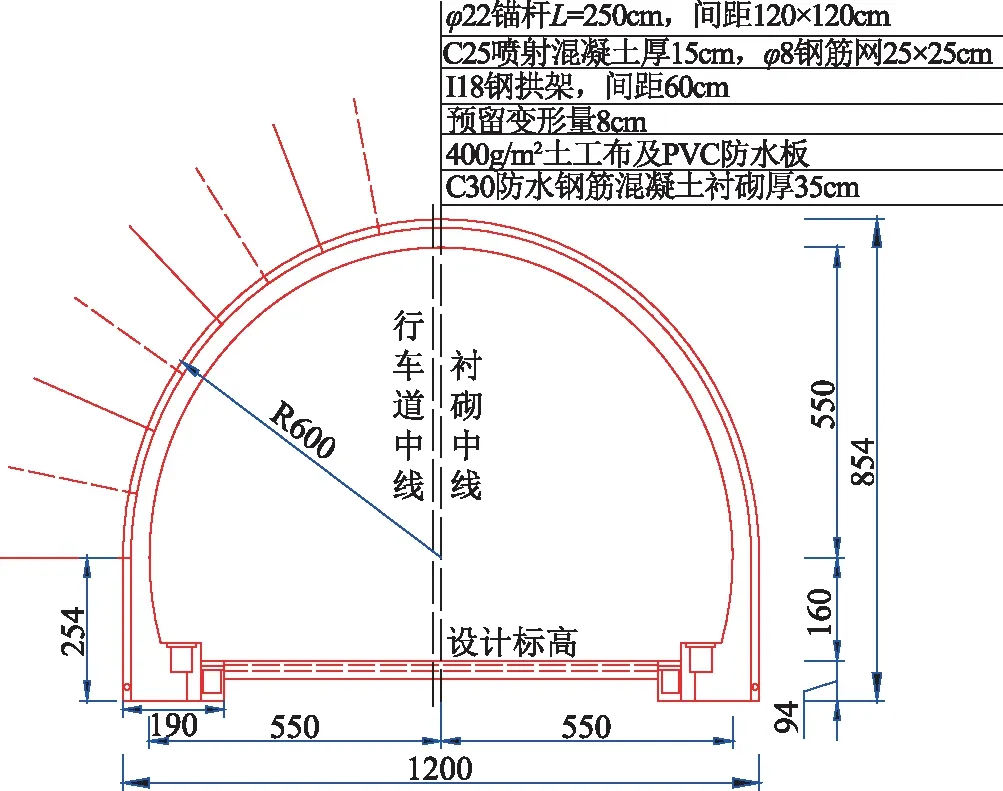
圖9 ZK25+200～300段支護結構橫斷面圖(單位：cm)

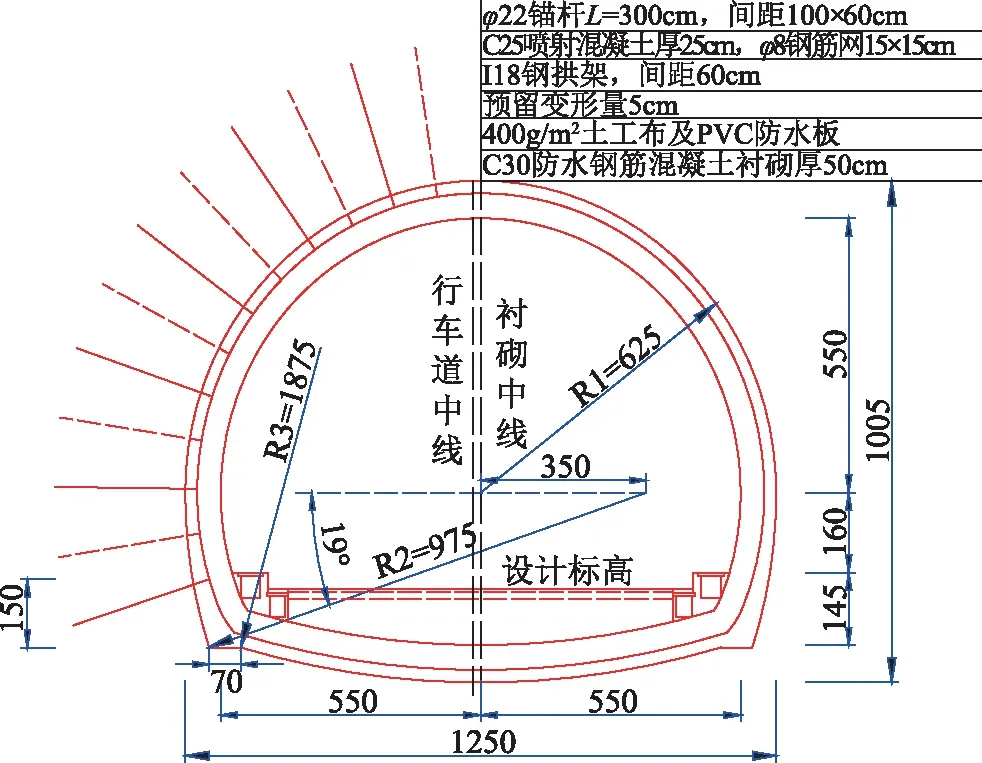
圖10 ZK20+860～21+000段支護結構橫斷面圖(單位：cm)

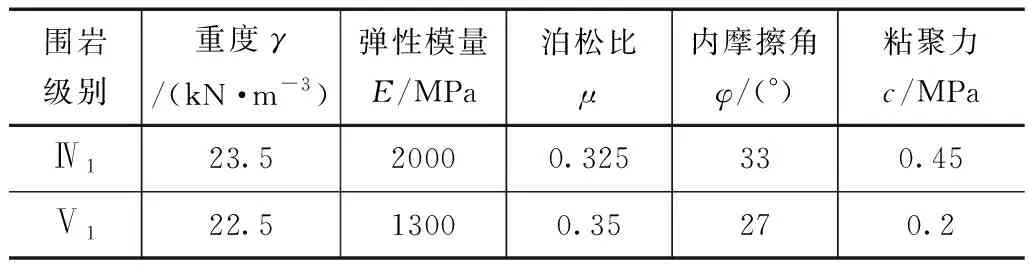
表3 Ⅳ1、Ⅴ1級圍巖物理力學參數

6.1 ZK25+200～300段

該段隧道斷面面積S=87.03m2，通過式(22)可得其等代圓半徑為5.79m。根據其初期支護參數，C25噴射混凝土彈性模量Ec=2.8×104MPa，抗壓強度25.1MPa，厚度為15cm，泊松比為0.2。φ22錨桿彈性模量E=210×103MPa，長度為l=250cm，間距120cm×120cm，破壞荷載Qbf=196kN，錨固端和錨固頭的荷載-變形常數η=4.2×10-5m/kN。

代入式(23)—(28)得：

Kc=133.082MPa/m，Pmax，c=0.650MPa，ulim，c=4.89mm。Kb=9.472MPa/m，Pmax，b=0.136MPa，ulim，b=14.37mm。由式(32)、(33)得組合支護系統剛度K=142.554MPa/m，最大支護阻力Pmax=0.6966MPa。

利用圍巖穩定安全系數(Q1)、初期支護安全系數(Q2)和圍巖變形控制率(Ψ)三者對開始施作初期支護的距離進行綜合評價。在分別距離掌子面0、1、2、3、4、5m處開始施作初期支護，其圍巖及支護系統安全系數如圖11所示。

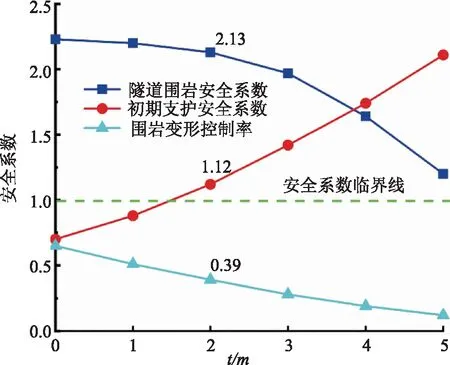
圖11 不同支護起點對應Q1、Q2、Ψ

由圖11可知，在0m及1m處，Q2小于1，即在安全系數臨界值以下，表示其支護系統在隧道穩定之前即達到了其支護阻力極限值，發生了破壞。2m以后，在平衡時支護系統有了安全盈余，但Q1和Ψ均逐漸降低，故選擇在距離掌子面2m處開始施作初期支護。此時，該段隧道圍巖特征曲線及支護結構特征曲線如圖12所示。

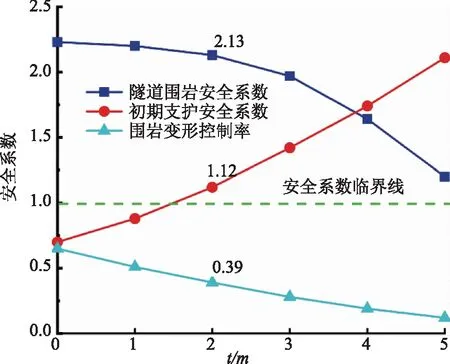
圖12 ZK25+200～300段收斂-約束曲線

由圖12可知，此時Q1=2.13，Q2=1.12，Ψ=0.39，圍巖處于較安全的狀態，初期支護系統亦有一定的安全盈余，說明初期支護起點距離掌子面2m是合理的。

6.2 ZK20+860～21+000段

該段隧道斷面面積S=103.83m2，通過式(22)可得其等代圓半徑為6.32m。根據其初期支護參數，C25噴射混凝土厚度為25cm；φ22錨桿，長度為300cm，間距100cm×60cm，噴射混凝土及錨桿其它參數同第6.1節。I18鋼拱架彈性模量E=210×103MPa，橫截面面積30.756cm2，橫截面高度h=18cm，間距60cm，屈服強度σs=268MPa。

代入式(23)—(31)得：

Kc=187.829MPa/m，Pmax，c=0.992MPa，ulim，c=5.28mm；Kb=20.943MPa/m，Pmax，b=0.327MPa，ulim，b=14.37mm；Ks=27.701MPa/m，Pmax，b=0.220MPa，ulim，b=7.96mm；由式(32)、(33)得組合支護系統剛度K=236.472MPa/m，最大支護阻力Pmax=1.249MPa。

同第6.1節，在分別距離掌子面0、1、2、3、4、5m處開始施作初期支護，其圍巖及支護系統安全系數如圖13所示。

圖13 不同支護起點對應Q1、Q2、Ψ

圖14 ZK20+860～21+000段收斂-約束曲線

由圖13可知，Q2逐漸增大，且在0m處，Q2即大于1，表示在掌子面處施作支護系統時，隧道穩定后支護結構亦有一定的安全盈余。Q1和Ψ均逐漸降低，在l=3m時，Q1突破了安全系數臨界線，此時隧道圍巖已經達到允許極限位移值，已經失穩。考慮新奧法“少擾動，早支護，勤量測，緊封閉”的施工原則，故選擇在掌子面處即開始施作初期支護。此時，該段隧道圍巖特征曲線及支護結構特征曲線如圖14。

由圖14可知，此時Q1=5.85，Q2=1.39，Ψ=0.45，圍巖處于較安全的狀態，初期支護系統亦有一定的安全儲備，說明在掌子面處施作初期支護是可行的。

7 結論

(1)本文基于彈塑性模型推導了深埋圓形隧道的圍巖特征曲線解析式，并結合“當量半徑法”得到了非圓形斷面隧道的等價圓半徑，實現了非圓形隧道荷載-位移關系曲線的轉化求解。

(2)利用GRC、SCC和LDP的對應關系，給出了初期支護結構設計的步驟，可為隧道初期支護設計提供指導。

(3)引入圍巖穩定安全系數、支護結構安全系數和圍巖變形控制率，對初期支護結構的合理支護起點的選擇進行綜合評價。

(4)定性分析了圍巖級別、隧道埋深和隧道洞徑對圍巖特征曲線的影響。發現圍巖所需支護力與圍巖級別呈正比，而初始地應力與圍巖級別呈反比；隧道埋深對圍巖特征曲線的影響較明顯；隧道洞徑愈大，圍巖塑性區愈廣，塑性變形愈大。

(5)利用文章理論成果對白巖腳隧道初期支護結構的合理支護起點進行了選擇分析。發現對于ZK25+200～300段，合理支護起點是距離掌子面2m處，此時Q1=2.13，Q2=1.12，Ψ=0.39，圍巖處于較安全的狀態；對于ZK20+740～850段，合理支護起點就是掌子面處，此時Q1=5.85，Q2=1.39，Ψ=0.45，圍巖處于較安全的狀態，且初期支護系統亦有一定的安全儲備。

(6)將噴射混凝土、錨桿和鋼拱架等單元剛度簡單疊加作為組合支護結構剛度，存在一定的誤差，后續研究需進一步優化。