基于Matlab輔助的“計算機控制技術”教學方法探討：以“最少拍控制系統”設計為例＊

朱家驥，李愛琴，段小匯

（鹽城工學院電氣工程學院，江蘇 鹽城 224051）

“計算機控制技術”是自動化類專業的核心課程之一，涉及的知識面廣，知識集成度高，在專業課程體系中占舉足輕重的地位。近年來，隨著計算機技術、控制技術、信息技術、通信技術的不斷發展及其相互之間的滲透和影響，極大地推動了計算機控制技術的迅猛發展。同時，以計算機控制技術為基礎的計算機控制系統在軍事、工業、農業、交通運輸等各個領域獲得了廣泛的應用[1]。基于這樣的應用需求，社會對掌握計算機控制技術的高素質人才的需求不斷擴大。由此可見，“計算機控制技術”課程教學效果的優劣對自動化類專業學生綜合應用能力的培養會產生直接影響。

1 課程特點及教學方法探討

“計算機控制技術”是一門理論性和實踐性都很強的綜合性課程，與“模擬電路”“數字電路”“單片機原理與技術”“微機原理與接口技術”及“自動控制原理”等諸多專業課程都有關聯[2]。它主要包含2部分內容：①計算機控制理論基礎。該部分內容包括采樣定理、Z變換、脈沖傳遞函數、離散系統分析、數字控制器設計方法等。②實現技術。該部分內容包括模擬量輸入與輸出通道、數字量輸入與輸出通道、數據處理與數字濾波等。這其中，計算機控制理論概念抽象、公式變換煩瑣、數學計算量大，學生在學習過程中普遍反映理論知識枯燥，難以理解和掌握[3]。因此，對于“計算機控制技術”任課教師而言，選擇合適的教學方法和手段是非常重要的一項任務與挑戰。

本課程的教學目標是希望學生能夠掌握計算機控制系統設計的步驟、方法以及分析問題、解決問題的能力，很顯然，通過單純的板書講解很難實現這一教學目標。鑒于此，借助軟件進行輔助教學是非常有必要的，考慮到Matlab軟件具有強大的數值、符號運算及圖形處理等功能，目前已成為大學教學中常用的計算機輔助教學軟件。因此，本課程嘗試在課堂教學中采用傳統板書講授理論為主、Mtalab軟件仿真為輔的模式，在此基礎上穿插實際案例分析的教學方法，使教學內容形象直觀、易于理解，以期提高教學質量，促進學生學習的積極性與主動性[4]。

2 案例分析

2.1 最少拍控制系統設計

最少拍控制系統設計是“計算機控制技術”課程的教學重點和難點內容之一，是控制器數字化設計方法的典型代表，在工業領域中最少拍控制系統常被應用于隨動系統、伺服系統、運動控制系統等系統中[5]。最少拍控制系統設計的具體要求是：①最少拍控制器的設計是在給定輸入信號的情況下進行的，且在到達穩態后，系統在采樣點的輸出值準確跟蹤輸入信號，不存在靜差；②各種使系統在有限拍內到達穩態的設計中，系統準確跟蹤輸入信號所需的采樣周期數應為最少；③最少拍控制器必須在物理上可以實現；④最少拍控制器與被控對象一起構成的閉環系統必須是穩定的[6]。

假設典型的數字控制系統框圖如圖1所示，在此基礎上，最少拍控制系統設計步驟總結如下[7]。

圖1 數字控制系統框圖

步驟1，計算廣義對象脈沖傳遞函數G（z），公式為：

步驟2，如果廣義對象脈沖傳遞函數G（z）有l個采樣周期的純滯后，有i個單位圓上及圓外的零點z1，z2，…，zi，j個單位圓上及圓外的極點p1，p2，…，pj，則：

步驟3，先由式（6）和式（7）確定Φ0（z）和F（z）中z-l的最高次冪，其中m是由輸入信號的類型確定的，如果輸入信號為單位階躍信號，則m=1；如果輸入信號為單位速度信號，則m=2；如果輸入信號為單位加速度信號，則m=3。然后將式（2）代入式（3）中，獲得恒等式及其對應的方程組，計算確定Φ0（z）和F（z）中的參數。

步驟4，由Φ0（z）、F（z）以及廣義對象的純滯后時間、單位圓外的零點和極點確定Φ（z）和1-Φ（z）的具體表達式。

步驟5，計算最少拍控制器脈沖傳遞函數D（z），公式為：

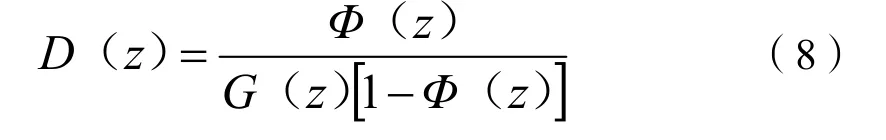
步驟6，計算系統輸出信號的脈沖傳遞函數Y（z）和最少拍控制器輸出信號的脈沖傳遞函數U（z），即：

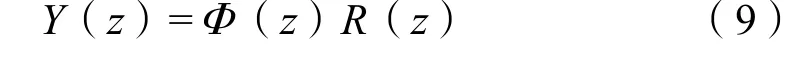
式（9）（10）中：R（z）為輸入信號的z變換。

雖然上述一般設計方法中考慮了被控對象有單位圓上零、極點（臨界點）的情況，但由于系統中總存在阻尼，這些臨界點是允許存在的。同時，考慮到設計的控制器不能過于復雜，故在上述步驟2中只考慮被控對象有單位圓外零、極點的情況，對被控對象單位圓上零、極點不做處理。

2.2 最少拍控制器解析法計算

系統的廣義對象脈沖傳遞函如下：

由廣義對象脈沖傳遞函數G（z）可知：G（z）無純滯后環節，即l=0；G（z）無單位圓外的極點，即j=0；G（z）無單位圓外的零點，即i=0。由于本系統參考輸入為單位階躍信號，則m=1。由式（6）和式（7）可得s=1，t=0。

由式（2）可知，Φ（z）的表達式為：Φ（z）=Φ0（z），其中，由式（4）可知Φ0（z）=m1z-1，故Φ（z）=m1z-1。

由式（3）可知，1-Φ（z）的表達式為1-Φ（z）=（1-z-1）F（z），其中，由式（5）可知F（z）=1，故1-Φ（z）=1-z-1。

由2個獨立表達式Φ（z）和1-Φ（z）可解得ml=1，故Φ（z）=z-1。在此基礎上，可由式（8）得到最少拍控制器脈沖傳遞函數D（z）的表達式，即：

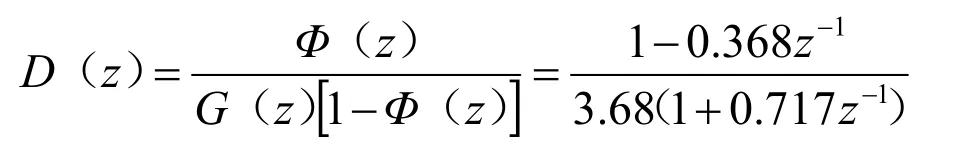
由式（9）可得系統輸出信號的脈沖傳遞函數Y（z）的表達式，即：

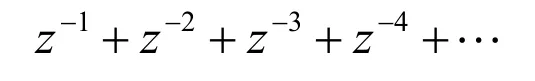
由式（10）可得最少拍控制器輸出信號的脈沖傳遞函數U（z）的表達式，即：

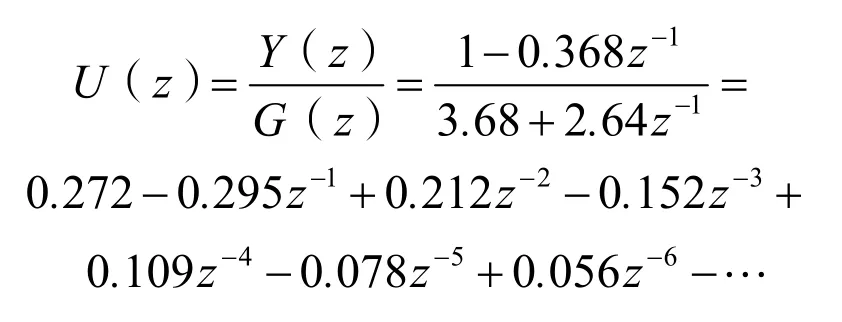
綜上所述，由Y（z）可知，系統輸出在一拍后達到無靜差的穩態；由U（z）可知，雖然控制量是收斂的，系統是穩定的，但由于控制量是波動的，實際上輸出量在采樣點之間也是波動的，即系統輸出存在紋波。

2.3 最少拍無紋波控制器解析法計算

最少拍控制器只能保證在采樣點上的穩態誤差為0，在許多情況下，系統在采樣點之間的輸出呈現紋波，這不但使實際控制不能達到預期目的，而且增加了功率損耗和機械磨損。系統輸出在采樣點之間存在紋波，主要是由控制量序列的波動引起的，其根源在于控制器的脈沖傳遞函數中含有非零極點。設計最少拍無紋波控制器時，處理這些非零極點的具體方法是：選擇閉環脈沖傳遞函數Φ（z）除了按上述的方法進行外（以保證控制器的可實現性及閉環系統的穩定性），像處理單位圓外的零點那樣，還應將廣義對象脈沖傳遞函數G（z）在單位圓內的非零零點包括在Φ（z）中，以便在控制器的脈沖傳遞函數中消除引起振蕩的所有極點。依據此思想，且在2.2節的基礎上進行最少拍無紋波控制器的設計。

由2.2節中計算得到的廣義對象脈沖傳遞函數G（z）可知，其存在一個單位圓內的零點z=-0.717，在設計最少拍控制器中，選擇Φ（z）時并沒有考慮該零點，從而使控制器的脈沖傳遞函數F（z）中有一負實部的極點z=-0.717，造成了控制量序列的上下波動。在設計最少拍無紋波控制器中，為了消除紋波，取Φ（z）=（1+0.717z-1）m1z-1。由于Φ（z）中z-1的冪次增加了一階，所以1-Φ（z）=（1-z-1）（1+f1z-1）。

由此可以解出，ml=0.58，fl=0.42，故Φ（z）=0.58z-1+0.42z-2。在此基礎上，可由式（8）得到最少拍無紋波控制器脈沖傳遞函數D（z）的表達式：

由式（9）可得系統輸出信號的脈沖傳遞函數Y（z）的表達式，即：

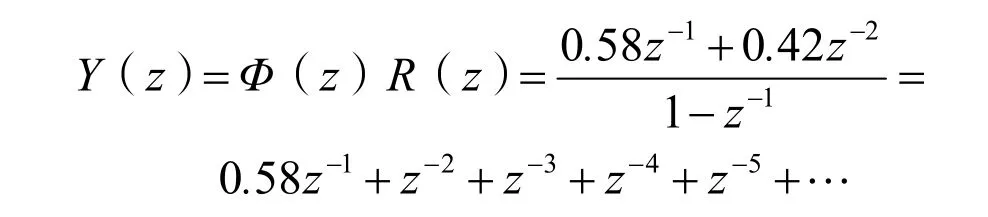
由式（10）可得最少拍無紋波控制器輸出信號的脈沖傳遞函數U（z）的表達式，即：

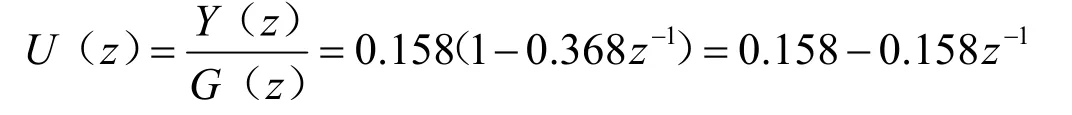
綜上所述，系統的輸出量序列為0、0.58、1、1、…，控制量序列為0.158、-0.058、0、0、…，系統在兩拍之后才達到穩態，調節時間比原來的系統增加了一拍，但紋波卻消除了，即控制量不再波動。

3 軟件輔助設計與仿真

本節以圖1所示的數字控制系統框圖為基礎，對第2節中所述案例采用Matlab/Simulink進行輔助設計與仿真。

3.1 最少拍控制器Matlab/Simulink輔助設計與仿真

由2.2節中最少拍控制器解析法設計過程可知，該方法設計步驟煩瑣，計算量很大，任何一個步驟出現錯誤都將造成整個系統出現錯誤。實際上，最少拍控制器的設計完全可以由Matlab編程實現，Matlab編程實現的程序代碼如下：

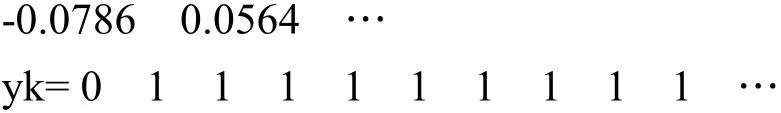
將上述結果與2.2節中解析法計算的結果進行對比，很明顯，通過采用Matlab編程輔助設計的整個過程既快速，獲得的結果又準確。同時，為了加深學生對理論計算方法的理解，可以采用Matlab中的Simulink功能對最少拍控制系統進行建模仿真。圖2為本示例中最少拍控制系統的Simulink仿真實驗模型，該模型運行后得如圖3所示的仿真實驗結果。

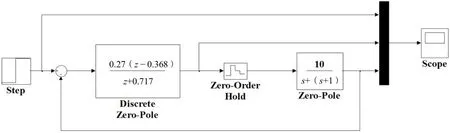
圖2 最少拍控制系統Simulink仿真實驗模型

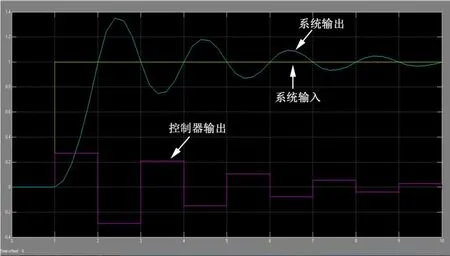
圖3 最少拍控制系統的輸入、輸出及數字控制器的輸出曲線

圖3采用Simulink建模仿真實驗得到的最少拍控制系統的輸入信號曲線、數字控制器D（z）的輸出u（k）曲線和系統輸出y（k）曲線。

如果單純地進行理論推導與計算，學生對最少拍控制系統各環節輸出的具體含義將很難理解，通過仿真實驗輸出的可視化效果，一方面使得輸出結果更直觀、更形象，另一方面有助于學生對最少拍控制器設計方法的理解與掌握。

3.2 最少拍無紋波控制器Matlab/Simulink輔助設計與仿真

由2.3節中最少拍無紋波控制器解析法設計過程可知，該方法設計步驟煩瑣，計算量很大，故在本節中采用Matlab編程實現最少拍無紋波控制器的設計，Matlab編程實現的程序代碼如下：

將上述結果與2.3節中解析法計算的結果進行對比，很明顯，通過采用Matlab編程輔助設計的整個過程既快速，獲得的結果又準確。

同時，為了加深學生對理論計算方法的理解，可以采用Matlab中的Simulink功能對最少拍無紋波控制系統進行建模仿真。圖4為本示例中最少拍無紋波控制系統的Simulink仿真實驗模型，該模型運行后得如圖5所示的仿真實驗結果，包括系統輸入信號曲線、數字控制器D（z）的輸出u（k）曲線和系統輸出y（k）曲線。

圖4 最少拍無紋波控制系統Simulink仿真實驗模型

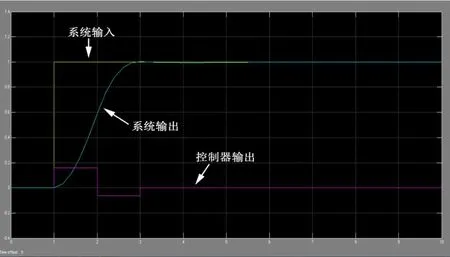
圖5 最少拍無紋波控制系統的輸入、輸出及數字控制器的輸出曲線

4 結束語

通過對“計算機控制技術”課程特點的分析，探索了教學方法的改進措施，并在教學過程中付諸了實踐。本文以最少拍控制系統（包括最少拍控制器和最少拍無紋波控制器）設計為教學案例，采用基于Matlab/Simulink的輔助設計與仿真實驗，加深了學生對最少拍控制系統設計方法的理解，促進了學生對該方法的掌握，從學生現場真實的實驗結果與課后作業情況以及期末考試中可以看出，取得了較好的教學效果。希望在今后的教學研究和教學實踐中，能進一步探索出更好的教學方法，提高學生分析問題、解決問題的能力，達到“新工科”教育背景下自動化類專業的培養目標。