改進混合粒子群算法求解旅行商問題

徐福強，鄒德旋，章猛，羅鴻赟

（江蘇師范大學 電氣工程及自動化學院，江蘇 徐州 221116）

0 引言

旅行商問題（TSP）是典型的NP-難問題［1］，也是經典的組合優化問題，故具有廣泛的應用背景，如計算機聯網、交通運輸、電氣布線、路線規劃等［2］。獲得高效的TSP 求解算法是組合優化領域的一個研究熱點，目前求解TSP 的方法主要分為兩大類。第一類是傳統的精確算法，主要有分支定界法、線性規劃法、動態規劃法等［3］。但是隨著TSP 中城市規模的增大，該類算法的求解能力顯著下降。第二類是近些年來隨著人工智能的發展而興起的智能優化算法，主要有遺傳算法（GA）［4］、蟻群算法（ACO）［5］、粒子群算法（PSO）［6］、模擬退火算法（SA）［7］等，現已廣泛地應用于TSP 求解，并且取得了很好的效果。

由于PSO 具有搜索迅速、容易實現、參數設置簡單等優點［8］，故對利用PSO 來解決TSP 的研究有著重要意義。但考慮到PSO 最初是用于連續型問題求解，而TSP 是離散型的組合優化問題。針對這個問題，近年來不斷有學者提出了適用于解決TSP的改進PSO。例如，高尚等學者［6］結合遺傳算法、蟻群算法和模擬退火算法的思想，提出用混合粒子群算法來求解TSP，并且在遺傳算法的交叉和變異的策略選擇上進行了詳細的介紹，但其解決TSP 的問題規模太小，并未驗證該算法在大規模TSP 上的實用性。鄧偉林等學者［9］提出一種離散粒子群算法來解決TSP，重新定義了速度及其粒子位置的相關算子，并設計距離排序矩陣來指導粒子進行高效的全局搜索，但是其參數設置較為復雜，算法收斂速度較慢。裴皓晨等學者［10］提出一種引入混沌算子的改進混合粒子群算法優化來解決TSP，可使搜索的范圍擴大，提高了搜索到更高質量解的概率，但在求解規模稍大的TSP時，解的質量明顯下降。Wei等學者［11］將概率初始化策略和遺傳算子引入到粒子群優化算法中，提出一種解決TSP 的改進混合粒子群算法，在算法迭代過程中節省了更多計算資源，增加了種群的多樣性并提高了算法的收斂精度，但在解的質量和求解穩定性上還有不足。

針對以上所述的解決TSP 的各種改進粒子群算法的優缺點，本文提出了結合貪心策略［12］、動態學習概率、Metropolis 準則［13］和2-opt 局部優化［14］的改進混合粒子群算法。依據貪心策略對種群進行初始化可以得到更高質量的搜索空間，一定程度上保證了解的質量；加入動態學習概率來平衡粒子群算法中的個體學習和群體學習；在個體學習和群體學習的過程中采用Metropolis 準則來依一定概率接受劣解，不僅增加了種群多樣性也提高了算法在搜索過程中跳出局部最優的能力；變異的部分采用2-opt 局部優化的策略可以消除路徑中出現交叉的現象，增強局部搜索能力，并進一步提高全局解的質量。最后，通過Matlab 將本文改進算法和其他4 種智能優化算法在TSPLIP 中的8 個實例上進行了仿真測試，證明了本文改進算法在求解精度、解的穩定性上具有更好的表現，并且對大規模的TSP 也具有較好的求解能力。

1 旅行商問題描述

旅行商問題最早由Flood［15］在1956 年提出，是一個具有代表性的離散組合優化問題。可以描述為一個商品的推銷員要去若干城市推銷商品，隨機選擇某一個城市作為起點，從該城市出發，要求經過所有的城市并且只經過一次，最后再回到起點城市。也就是構成一個哈密頓回路［16］，關鍵在于找到一條滿足條件的行進路線使得整個回路的路徑長度最短。

從圖論的角度來描述TSP［17］如下：設圖G＝（V，E），這里V表示所有城市組成的頂點集，E是集合V中元素（城市）兩兩相連組成的邊集，設每2個城市之間的距離記為則求解TSP 的數學模型可表示為：

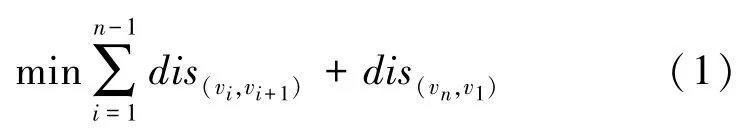
式（1）中的第一項是對從1到n個城市計算最短的路徑距離和，式（1）中的第二項是計算第n個城市回到第一個城市的距離，這2 項相加構成一個完整的回路路徑長度。

2 算法分析

2.1 粒子群算法

PSO 是一個由Kennedy 和Eberhart 在1995 年提出的群體智能優化算法［18］。其基本思想是先隨機初始化一群粒子，每個粒子都具有速度和位置以及由目標函數決定的適應度值這3 個屬性，再引入個體極值和群體極值的2 個概念。在每次迭代過程中，根據式（2）和式（3）來更新每個粒子的速度和位置，然后計算適應度值，并根據目前的適應度值來更新個體極值和群體極值，再經多次迭代，搜索到目標函數的最優解。標準PSO 的速度與位置的更新公式如下：

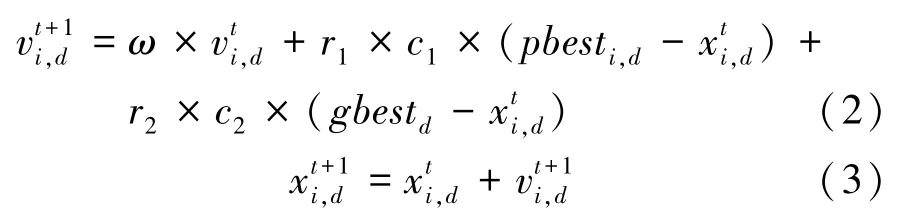
2.2 遺傳算法

遺傳算法是由Holland 教授［19］在所著的《自然界和人工系統的適應性》中首先提出的。是一種受到生物界自然選擇和自然遺傳現象啟發的隨機搜索算法。算法模仿自然遺傳現象中的繁殖、交叉和基因突變的情況［20］，根據一定的標準來進行選擇和保留較好的候選解，此后再經過不斷地重復迭代，直至找到最優解或者滿足終止條件為止。

2.3 解決TSP 的混合粒子群算法

混合粒子群算法就是把遺傳算法和粒子群算法進行了融合，通過遺傳算法的交叉操作和粒子群算法中的個體學習和群體學習來對每代粒子個體進行優秀子代的產生和遴選；在此基礎上將通過遺傳算法的變異來替代實現粒子群算法中的位置更新操作，經多次迭代后找到TSP 的最優解。近年來，經過較多學者研究和大量的實驗仿真結果充分地證明了混合粒子群算法的有效性和先進性。但是其在求解TSP 的精度和穩定性方面還有一定的提升空間，并且對大規模TSP 的求解能力較差。

3 算法改進

3.1 基于貪心策略的種群初始化

智能群體優化算法一般是隨機生成初始種群，這樣容易使初始種群個體的適應度值與研究需要的最優解的適應度值出現很大的偏差。造成算法收斂速度的降低和運行耗時的增加，還會導致解的質量下降、甚至增加了算法陷入局部最優的可能。

本文采用基于貪心策略的種群初始化來有效地保證初始搜索空間的質量。具體方法是按照在TSP中兩城市間距離最短的思想來依次選定一個起始城市，然后在剩余城市中選取與上個選定城市距離最近的城市作為下一個城市，循序重復操作直至最后一個城市。這樣得到的城市序列作為改進混合粒子群算法的初始解，在一開始迭代的時候就具有較好的適應度值，有利于加快算法的收斂速度，提高算法求解精度。

3.2 加入動態學習概率

在粒子群算法中通過個體學習和群體學習來更新粒子的速度，個體學習有利于拓展粒子的搜索空間，群體學習有利于粒子朝全局做最優搜索。結合解決TSP 的具體情況，本文采取加入動態學習概率的方法調節與個體最優交叉及與群體最優交叉的進行，來更好地平衡個體學習與群體學習。動態學習概率的數學定義式如下：

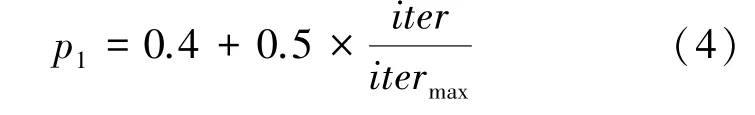
其中，iter表示目前的迭代次數，itermax表示算法設定的最大迭代次數。

通過式（4）可知，隨著迭代的不斷進行，p1會不斷變大，當取一個0～1 之間的隨機數大于p1時，與個體最優交叉，即個體學習；否則，與群體最優交叉，即群體學習。所以，算法迭代搜索的前期個體學習的概率更高，增加了種群的多樣性；到了算法迭代的后期，群體學習的概率更高，傾向于和群體最優進行交叉，利于算法的全局收斂。

3.3 采用Metropolis 準則接受劣解

由于混合粒子群算法在解決TSP時，容易陷入局部最優而導致算法收斂不到最優解。所以本文改進算法在個體學習和群體學習中采用Metropolis 準則來依概率p2接受劣解，從而在一定程度上豐富了種群粒子的多樣性，提高了算法跳出局部最優的能力。概率p2的數學表達式如下：

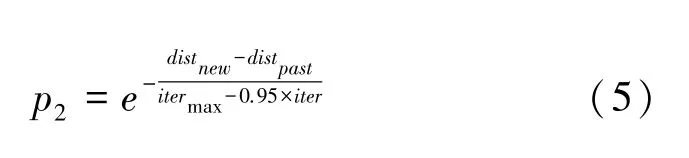
其中，distnew表示經過個體學習或群體學習產生的新城市序列對應的路徑長度；distpast表示之前的舊城市序列對應的路徑距離；隨著迭代的進行，itermax-0.95× iter的值在不斷減小，根據指數函數的特點，p2的值在逐漸減小，所以迭代到后期，接受劣解的可能性就不斷降低，保證了算法的收斂性。當distnew ＜distpast時，直接用新城市序列替換舊城市序列，實現算法朝距離最短的城市序列方向搜索。否則，在個體學習和群體學習中依據rand ＜p2的概率來接受distnew ＞distpast的城市序列。并且如果distnew -distpast的值較小，也就意味著新解和舊解對應路徑距離相差得小，p2值反而越大，則rand ＜p2的概率越大，接受該劣解的可能性就更大，并且該劣解經過此后的2-opt 局部優化得到更短路徑的可能性也越大。

3.4 2-opt 局部優化

TSP 中很容易出現路徑交叉的現象，并且路徑一旦有交叉勢必會導致整個路徑距離的增加，故而消除交叉現象的發生也是解決TSP 的重要一步。考慮到2-opt 局部優化的耗時性，本文對個體學習和群體學習后的粒子適應度值進行升序排列，取適應度值從小到大且20%種群規模數量的粒子進行2-opt局部優化。2-opt 局部優化操作示意如圖1 所示。

圖1中，圖1（a）表示原路徑，是經過個體學習或群體學習得到的目前搜索到的最好的城市序列：A→B→C→D→E→F→G→H→A，可以直觀地看出城市B和城市C及城市F和城市G之間有路徑交叉的現象；再觀察圖1（b）中的新路徑，就是把城市B和城市G的位置進行了調換，同時把原來城市B和城市G之間的城市序列順序進行了倒置。新的城市序列為：A→G→F→E→D→C→B→H→A。顯而易見，之前的交叉現象被消除了，路徑的長度也縮短了，故證明了2-opt 局部優化的有效性。

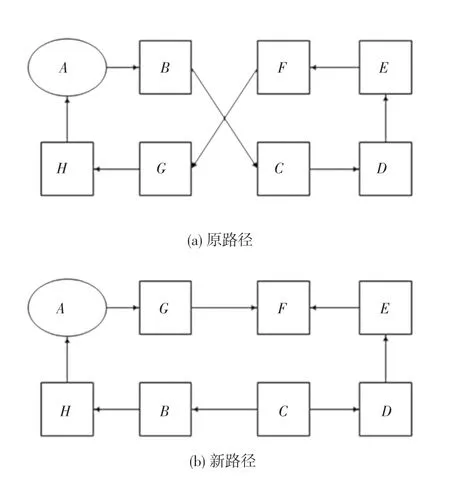
圖1 2-opt 局部優化操作示意圖Fig.1 Schematic diagram of 2-opt local optimization operation

本文采取2-opt 局部優化作為本文改進算法中的變異操作，同時也實現粒子群算法中綜合個體學習和群體學習后的位置更新操作。經過2-opt 優化后，比較選擇更短的城市路徑距離對應的城市序列，使得算法朝著全局最優搜索。

3.5 改進混合粒子群優化算法解決TSP 的步驟

步驟1加載TSP 實例和計算城市間距離。

步驟2算法初始化，包括種群的初始化，結合城市間的距離來基于貪心策略得到較高質量的初始種群，同時設置本文改進算法的最大迭代次數，作為算法結束的標志條件。

步驟3計算粒子適應度值，并確定個體最優和群體最優。

步驟4根據動態學習概率p1來進行學習策略的選擇，如果隨機數大于p1，則選擇個體學習，與粒子個體最優進行交叉，否則選擇群體學習，與群體最優進行交叉，并且在個體學習和群體學習中加入了Metropolis 準則，依概率p2來接受劣解。

步驟5對經過個體學習和群體學習的種群進行2-opt 局部優化操作，消除路徑交叉的情況，搜索更優解。

步驟6判斷是否達到算法終止條件，本文為設定的最大迭代次數，如果達到，輸出最優解及對應的最短路徑長度，否則返回步驟3，重復執行，直至滿足算法終止條件。

本文改進混合粒子群算法流程如圖2 所示。

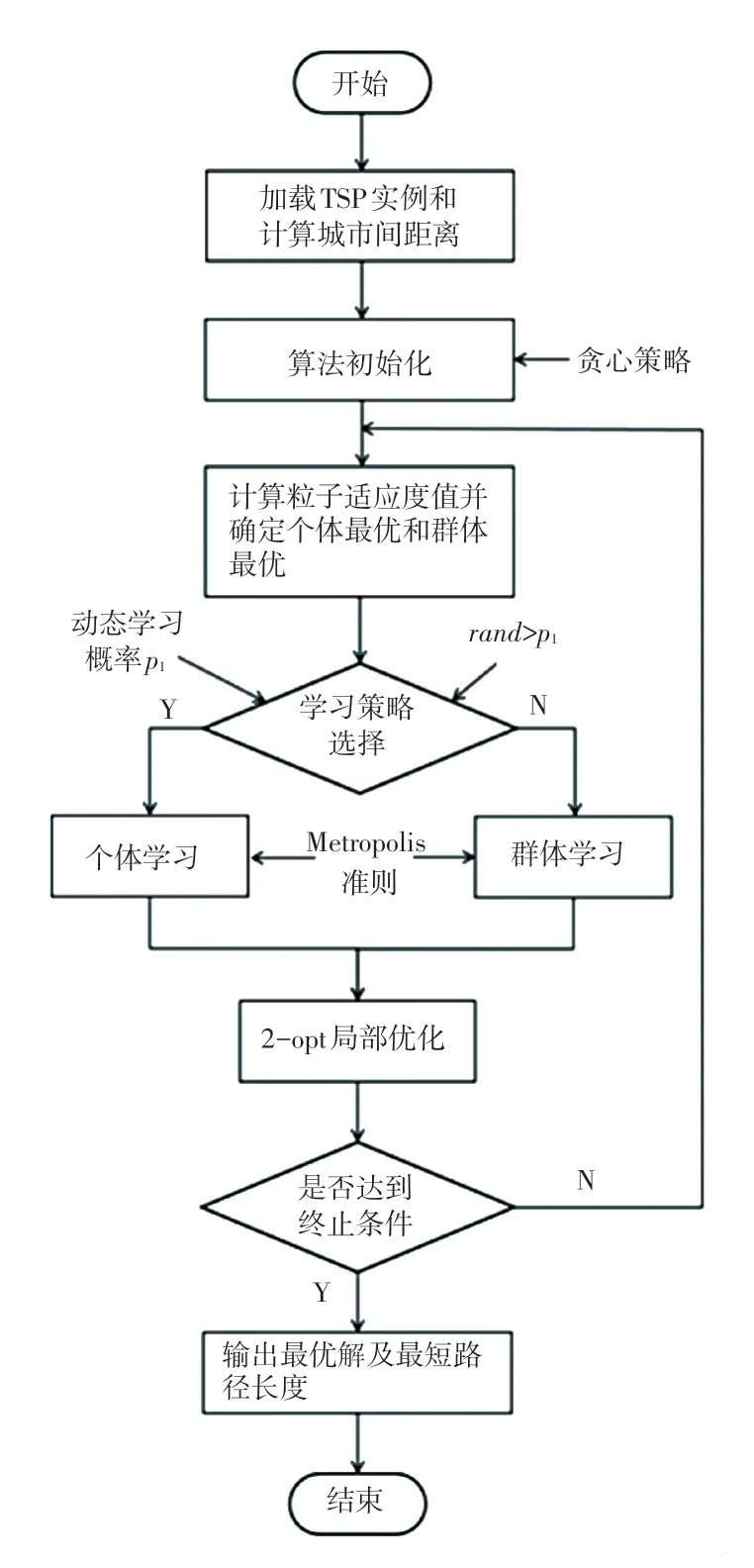
圖2 改進混合粒子群算法流程圖Fig.2 Flow chart of improved hybrid particle swarm optimization

4 仿真實驗及分析

4.1 仿真實驗基礎

根據以上分析，為了驗證本文改進混合粒子群算法解決TSP 的可行性與有效性，將混合粒子群算法、GA、ACO、SA 及本文改進混合粒子群算法在Matlab 仿真軟件上對TSPLIB 中的8 個不同城市規模的實例進行測試。

本文仿真實驗環境配置如下：硬件方面使用AMD Ryzen 7 5800H 3.2 GHz CPU，16 G RAM 的計算機；軟件環境基于Windows 10，Matlab R2019a。

本文仿真實驗選用了TSPLIB 中8 個不同城市規模的實例，從小到大分別是Oliver30，eil51，st70，eil76，eil101，ch150，pr226，pcb442。混合粒子群算法參數設置：種群規模取1 000，最大迭代次數取200，與個體最優交叉的概率取0.5，與群體最優交叉的概率取0.5，變異的概率取0.3；GA 參數設置：種群規模取1 000，最大迭代次數取200，交叉概率取0.7，變異概率取0.2；ACO 參數設置：螞蟻數量等于TSPLIB 實例中的城市個數，最大迭代次數取200，信息素重要程度因子取1，啟發函數的重要程度因子取5，信息素揮發因子取0.2；SA 參數設置：初始溫度61 ℃，結束溫度3 ℃，溫度衰減系數取0.985，馬爾科夫鏈長度取TSPLIB 實例中城市個數的100倍；本文算法參數：種群規模等于TSPLIB 實例中城市個數，最大迭代次數取200，動態學習概率為p1，Metropolis 準則中接受劣解的概率為p2，選取進行2-opt局部優化的粒子個數為種群規模的20%。

4.2 實驗結果與分析

經過以上分析，將5 種算法在8 個TSPLIB 實例上獨立運行30次，記錄每次的運行結果。對各算法在每個TSPLIB 實例上運行得到的30 個結果進行處理，找到最優解、最差解，計算出平均解，再結合TSPLIB 實例的已知最優解［21］，根據式（6）計算出平均偏差率。具體見如下：

5 種算法的實驗結果見表1。表1中，測試實例下面的括號中數值就是目前對應TSPLIB 實例的已知最優解。由表1 可以發現在解決實例Oliver30時，各算法搜索到的最優解都很接近已知最優解，并且平均偏差率都很小，說明各算法搜索的穩定性都還不錯，其中SA 的效果最好，略優于本文改進算法；而隨著TSP 規模的增加，各算法搜索到的最優解開始慢慢與已知最優解的偏差增大，其中混合粒子群算法和GA 體現得尤為明顯，當TSP 規模到100 及以上時，求解的質量很差，故而混合粒子群算法和GA 對ch150、pr226、pcb442 這3 個實例的實驗結果直接舍棄；雖然在本文仿真實驗中ACO 和SA求解了大規模TSP 的解，但是觀察表1 可知，ACO和SA 的最優解和偏差率都比本文改進算法的結果大，表明了本文改進算法對于解決大規模的TSP 具有更好的適應性和明顯優勢。

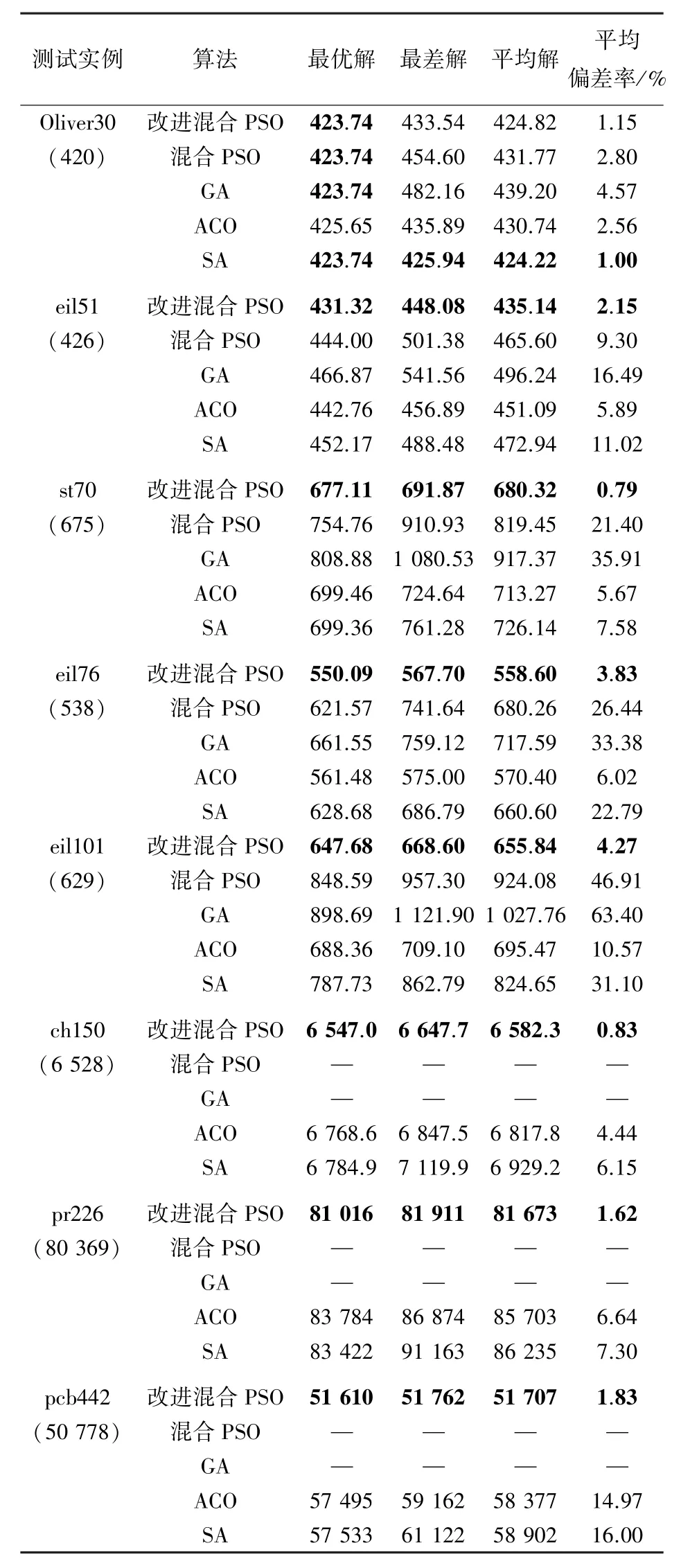
表1 算法實驗結果Tab.1 Experimental results of the algorithm

為了更加直觀地了解5 種算法解決TSPLIP 實例的過程情況，本文繪制出了5 種算法解決eil51、st70、ch150、pcb442 這4 個具有代表性的實例上的迭代曲線，如圖3～圖6 所示。觀察圖3 和圖4 可以發現，本文改進混合PSO 的初始解就具有很大優勢，并且收斂的速度要比其他4 種算法明顯更快，搜索到最優解的迭代次數更少，凸顯出算法的尋優能力較強。觀察圖5 和圖6 可知，當TSP 的規模較大時，本文提出的改進混合PSO 仍然具有很強的尋優能力。與ACO 和SA 相比，求解TSP 的質量更高，并且較少的迭代次數就可以搜索到最優解，表明了本文改進算法的適應能力強和求解精度高。為了直觀地考察本文改進算法的求解效果，根據上述分析做出對應的求解到的最優路徑圖如圖7～圖10所示。

圖3 eil51 迭代曲線圖Fig.3 Iteration curve of eil51

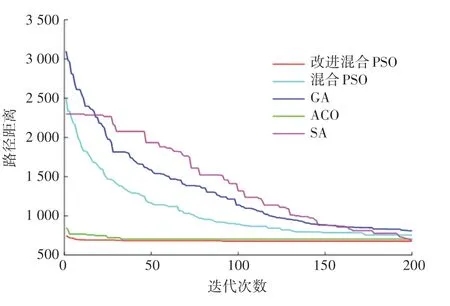
圖4 st70 迭代曲線圖Fig.4 Iteration curve of st70

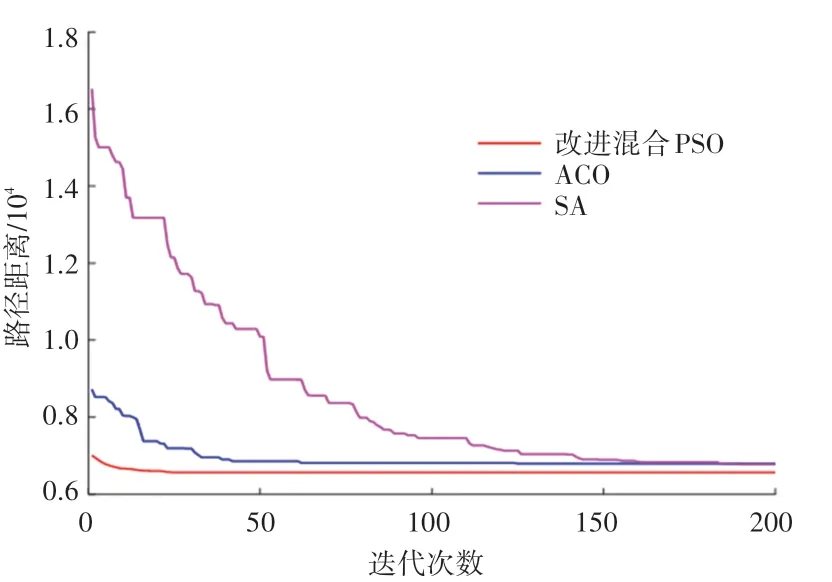
圖5 ch150 迭代曲線圖Fig.5 Iteration curve of ch150

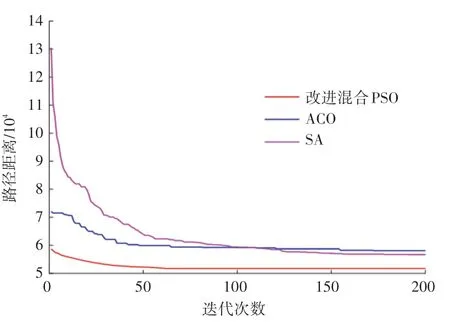
圖6 pcb442 迭代曲線圖Fig.6 Iteration curve of pcb442

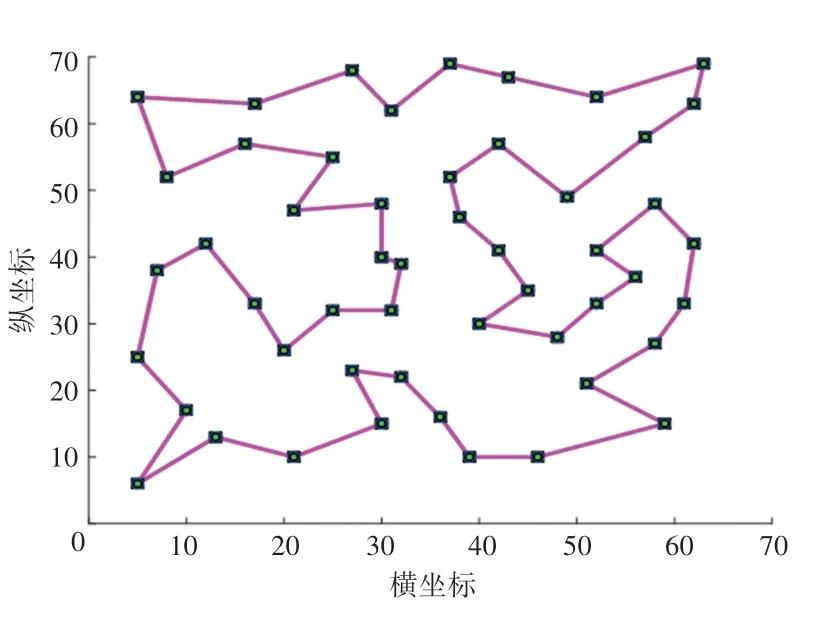
圖7 eil51 最優路徑圖Fig.7 Optimal path of eil51

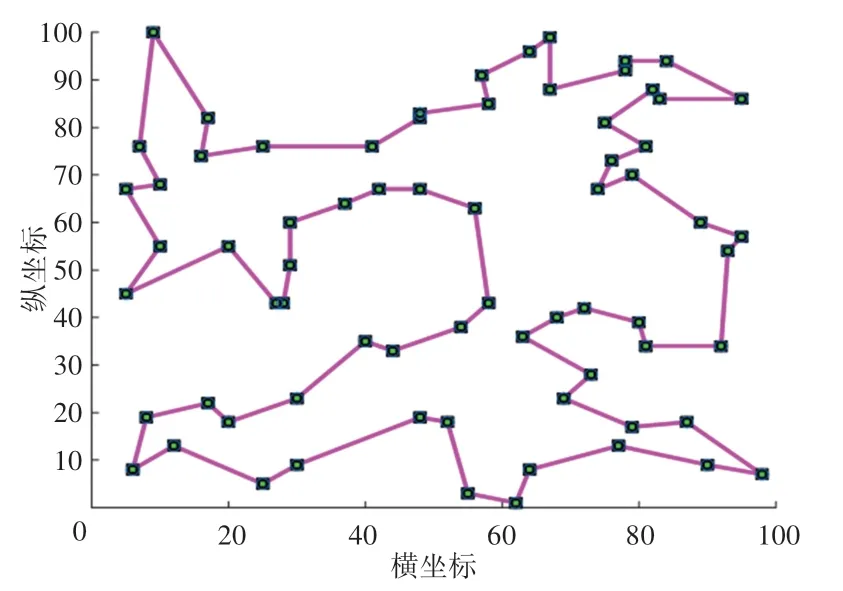
圖8 st70 最優路徑圖Fig.8 Optimal path of st70

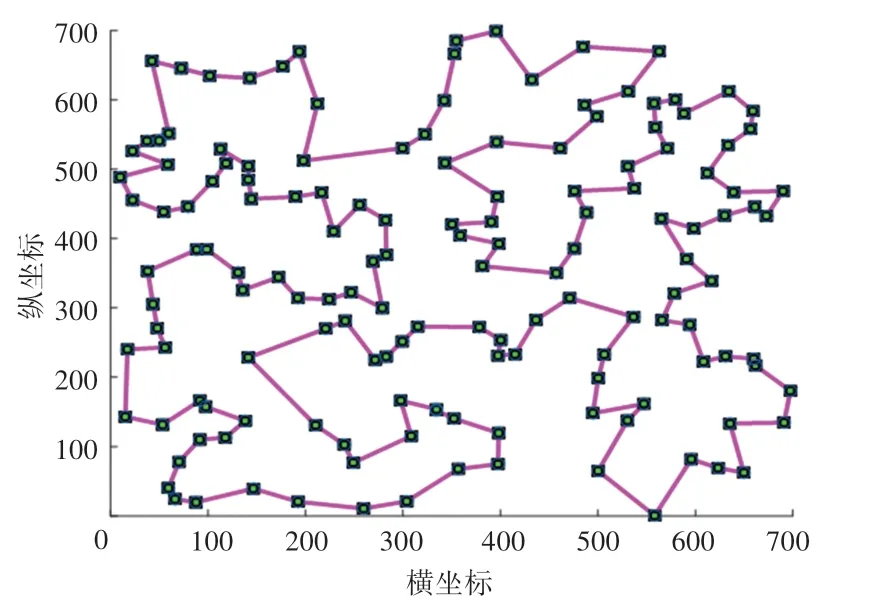
圖9 ch150 最優路徑圖Fig.9 Optimal path of ch150

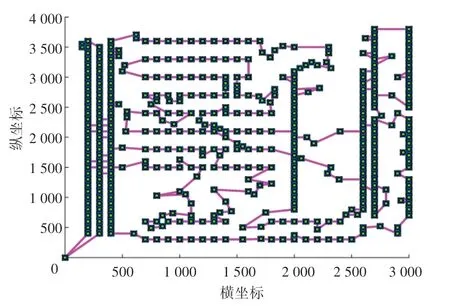
圖10 pcb442 最優路徑圖Fig.10 Optimal path of pcb442

5 結束語

本文提出了一種改進混合粒子群算法來解決旅行商問題，利用基于貪心策略的種群初始化很好地保證了算法搜索空間的質量；在算法的搜索過程中加入動態學習概率來選擇個體學習或群體學習，并在每個學習中引入Metropolis 準則來依一定概率接受劣解，既能增加種群粒子的多樣性，也能提高算法跳出局部最優的能力；再將經過個體學習和群體學習得到的城市序列進行2-opt 局部優化，有效地消除了城市路徑間出現交叉的現象，并且較好地保留更短的路徑及對應的城市序列，保證了算法朝著全局最優的方向進行收斂，提高了算法求解的精度。最后和其他4 種智能優化算法在Matlab 軟件上對TSPLIB 的8 個不同規模的實例進行了測試，仿真結果表明了本文改進算法的求解精度更高，算法的穩定性更好，并且更加適應于大規模TSP 的求解。