基于DNA編碼和二維混沌系統的圖像加密算法

唐浩哲 黃源源 任震宇 成江宇 李朝榮

(1.成都信息工程大學網絡空間安全學院,四川 成都 610225;2.宜賓學院人工智能與大數據學部,四川 宜賓 644000)

0 引言

近年來,隨著移動網絡時代不斷地飛速發展,人們能夠更便捷地獲取信息。然而,在與其他人交流互動的過程中,個人信息容易泄漏這個安全問題變得層出不窮。研究人員也隨之發現了網絡信息安全問題,并認為解決網絡信息安全以及傳輸中的問題刻不容緩。傳統的加密方法,如DES(data encryption standard,數據加密標準)、AES(advanced encryption standard,高級加密標準)等都只能保證應用在數據量較小的環境時,能夠有效保護多媒體版權,增強數據安全性[1]。

由于圖像所承載的信息具有高冗余度、巨大的數據存儲容量、較強的像素之間信息相關性等特點,所以使用圖像信息加密技術需要使用更加快速有效的加密算法。由此,傳統的圖像加密編碼方法(DES、AES等)已經無法滿足當前的數字圖像編碼加密安全性需求。

該領域的研究者在對圖像加密算法的實驗和研究中遇到過如下一些問題。

首先,CIE L*a*b*顏色空間在圖像處理和傳輸中都扮演了重要角色,被研究者應用到圖像的實驗和研究中。許莉等[2]提出了一種基于Lab顏色空間的運動目標檢測方法。通過選擇L*a*b*的顏色特征作為前景/背景進行分析的特征,分開處理亮度和色度,得到每個像素在各個通道上的不同信息;然后通過使用背景差和幀差相結合的查分監測模型對背景進行處理,最后通過背景差分得到運動圖像目標;不同的顏色空間也被加以應用,金漢均等[3]提出一種在HSV顏色空間中結合小波變換做的圖像檢索應用研究方法,但由于方法沒有融合圖像的多特征進行檢索,導致其準確度不高。

其次,通過應用DNA編碼來處理圖像,DNA編碼是將計算機科學與分子生物學相結合而產生的一個新興學科,通過模擬DNA生物操作,進行偽DNA計算來實現信息加密[4]。在實驗過程中,遇見了以下的一些問題:Zhang等[5]提出了一種基于DNA編碼和二維Logistic混沌映射的圖像加密算法,但發現這種算法得到的圖像難以抵擋已知明文的攻擊;田海江等[6]提出一種圖像加密算法通過基于普通混沌系統和DNA動態編碼,結果因DNA的運算規則不夠復雜,使得加密算法太過單一,圖像安全性也不高;因為其加密算法的不可逆現象,Bonny B R等[7]提出了一種基于DNA編碼的對稱密鑰加密算法,結果由于密鑰長度不夠,容易被暴力破解。

對于圖像加密,有不少學者也嘗試將混沌加密算法與人工智能領域中的DL(deep learning,深度學習)板塊相結合,通過卷積神經網絡的理論,使用足夠多的數據集去訓練加密算法或者超混沌系統,從而使算法處理后的加密圖像具有很高的安全性和抗噪能力。陳煒等[8]提出一種利用深度學習來壓縮重構圖像,再使用復合混沌系統、滑動置亂與矢量分解組成的加密算法對圖像進行加解密處理。但使用該算法加密的圖像并沒有得到很高的圖像信息熵值,加密圖像不具有足夠高的隨機性和安全性。

超混沌系統有很多特征:具有優秀的偽隨機性、對初始狀態及結構參數的極端敏感性以及其軌道具有不可預測特性等[9]。使用混沌序列成為隨機密鑰,能夠達到一次一密的效果。這樣的操作,在理論上是不可破的。然而,低維混沌序列存在許多問題,比如低維混沌序列會因計算機字節長度的限制,從而對混沌的動力學特性造成影響,使得加密算法不夠成熟;而且低維混沌系統產生的混沌只可短期預測,這讓其產生的混沌序列具有較差的隨機性,且獲得的密鑰空間小,加密后的結果安全性能低[10],易于破譯。相反,高維混沌系統能夠通過對更多的參數進行控制變化,提高圖像置亂的隨機性,從而增強圖像加密的安全性。因此,多維超混沌系統成為了一個很好的方法來確保混沌系統的復雜性。

為此,本文提出的基于DNA編碼和二維混沌系統組的圖像加密算法,結合了超混沌系統組(超混沌Chen系統、二維Logistic映射和廣義Arnold映射)和DNA編碼運算對目標加密圖像進行分塊加密。不僅能有效提高圖像加密過程密鑰的敏感性和傳輸過程中的安全性,還成功通過了包括差分攻擊在內的攻擊形式,以及灰度直方圖、相關系數計算分析等,具有較高的安全性。

1 基礎理論

1.1 CIE L*a*b*色彩空間

CIE L*a*b*是被常用來描述人眼可見的所有顏色的最完備的色彩模型[11]。即使目前絕大多數的彩色圖像信息的輸入和輸出均是根據RGB三色空間作為標準的,但是由于RGB三色通道均包含了其亮度信息,導致彩色圖像的三色間具有很強的相關性,從而影響圖像在后面部分加密置亂時無法得到一個更隨機安全性更高的的加密圖像。

CIE L*a*b*色彩空間是基于1931年的CIE XYZ色彩空間的一種更復雜的色彩空間,后者是采用X、Y、Z3個刺激值組成。X表示創建的非負曲線的圓錐體響應,Y表示亮度,Z表示藍色分量。由于RGB到CIE L*a*b*之間沒有直接的轉換公式,故需要先從RGB到CIE XYZ,再到CIE L*a*b*,以CIE XYZ作為顏色的中間層,起到起承轉合的作用。這兩個轉換步驟具體為

1.1.1 RGB—＞CIE XYZ

RGB和CIE L*a*b*色彩空間的轉換公式:

可見,XYZ和RGB在互相換算時,參數之和剛好為1。例如:X=0.433953×R+0.376219×G+0.189828×B,其中0.433953+0.376219+0.189828=1,這樣就做到了在轉換前后能夠獲得同等范圍的映射[12]。

1.1.2 CIE XYZ—＞CIE L*a*b*

CIE(國際照明委員會)在1964年提出了CIE L*a*b*均勻顏色空間。從XYZ到L*a*b*的轉換計算為

其中,Xn,Yn,Zn為CIE標準光源照射在完全漫反射體上后,再經過完全漫反射至觀察者眼中的三刺激值。通常情況下,Xn,Yn,Zn為常數且值均為255。另外,L∈[0,100],a∈[-127,127],b∈[-127,127]。真彩Lena圖像轉換至CIE L*a*b*色彩空間后的結果如圖1所示。

1.2 Chen混沌

2005年,通過狀態反饋控制構建了Chen氏混沌系統,其方程為

其中,x,y,z和ω作為系統的狀態變量,a,b,c,d和r為系統的控制參數。根據研究顯示:當a=35、b=3、c=12、d=7且0.085≤r≤0.798時,系統將表現為超混沌運動。

1.3 Logistic混沌系統

1.3.1 一維Logistic映射

單從數學式分析,一維Logistic映射是一個相當簡單的映射,但其實它在通信傳輸上擁有較高的復雜度。也有不少人在此基礎上研究圖像的加密問題,其數學公式為

Xn+1=Xn×μ×(1-Xn)

其中,μ作為Logistic參數,且μ∈[0,4],而研究表明,當變量X∈[0,1]時,此系統處于混沌狀態。

然而,在現在的各類攻擊手法作用下,普通的一維Logistic系統由于參數太少,無法生成復雜的混沌系統,無法使加密算法擁有較高的安全穩定性,因此本文將應用Logistic映射的二維混沌系統進行圖像加密。

1.3.2 二維Logistic映射

為保證加密后的圖像具有一定的安全性,引入一個新的二維Logistic函數。與現有的混沌映射相比,它具有更廣泛的范圍內混亂,更好的遍歷性和混沌性。其數學公式為

其中,μ、λ1、λ2和γ均為控制參數,通常情況下,取μ=4。經過計算得知:當λ1=0.9、λ2=0.9、γ=0.1時,此時的二維Logistic系統處于混沌狀態[13]。為了研究及其應用,提出一個置亂轉換(CMT),以有效地改變圖像的像素位置。結合二維Logistics與CMT,可以進一步實現圖像加密算法。

1.4 貓臉變換(Arnold)系統

1.4.1 離散Arnold變換

貓臉變換最早是由俄國數學家Arnold引入的,其數學式如公式為

其中,xn和yn均為實數且xn,yn∈(0,1),取模運算mod將(xn,yn)的相空間限制在 [1,1]×[1,1]內。

與一維Logistic混沌系統相同,離散Arnold映射因參數太少無法生成復雜混沌系統,無法有效保證加密過程的安全性。因此在文中使用廣義Arnold變換參與加密流程。

1.4.2 廣義Arnold變換

當然,Arnold映射同Logistic映射一樣,也是一種混沌映射[14]。其數學式為

其中,xn和yn是大小為N×N的圖像置亂前所處的像素位置,xn+1和yn+1為置亂后所處的像素位置,p,q,N均為正整數且p、q的值小于N。由于二維Arnold映射數字化是具有周期性現象[15],所以基于Arnold映射的圖像在加密時如果知道加密算法,通過在某一個密文空間以任意狀態進行迭代,都能夠在有限步驟中內被恢復為明文。例如:當p=40,q=8,N=124且iter=5(迭代輪數)時,此時加密圖像可恢復原樣,因而將Arnold映射和Logistic映射結合起來,能夠達到更好的加密效果。

1.5 DNA編碼規則和DNA基礎算法

1.5.1 DNA編碼規則

生物研究表明:DNA是由4種脫氧核苷酸通過堿基互補配對組成的雙螺旋鏈式結構。4種脫氧核苷酸分別為腺嘌呤(A)、鳥嘌呤(G)、胸腺嘧啶(T)和胞嘧啶(C),堿基互補配對規則為A與T配對、G與C配對。根據電腦二進制中1和0互補的特性可以利用DNA的堿基互補原則,用兩位二進制數值來表示4種脫氧核苷酸,且由于不同規則的核苷酸的二進制數值指定是不同的,所以滿足堿基互補配對的規則組合有8種[16],如表1所示。由于圖像在計算機中是由像素組成,且每個像素值都可以通過編制DNA單鏈來加密,然后通過互補單鏈來解密。以灰度值來舉例:設一個像素的灰度值為8bit,其二進制表示為“11000101”,用表1的規則1來編碼,可得編碼為“TACC”。

表1 DNA編碼規則

1.5.2 DNA基礎運算

整個加密過程中可能使用到的DNA編碼運算方法分為DNA的加法、DNA的減法和DNA的異或。DNA的加法、減法和異或運算類似于傳統的代數運算[17],運算規則如表2～4所示。

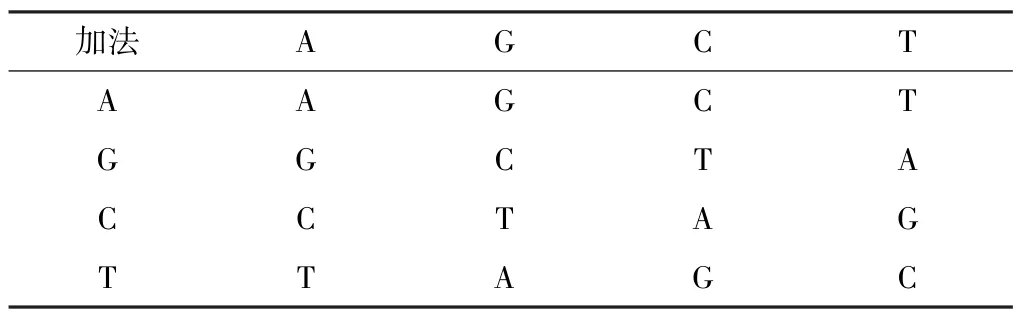
表2 DNA加法

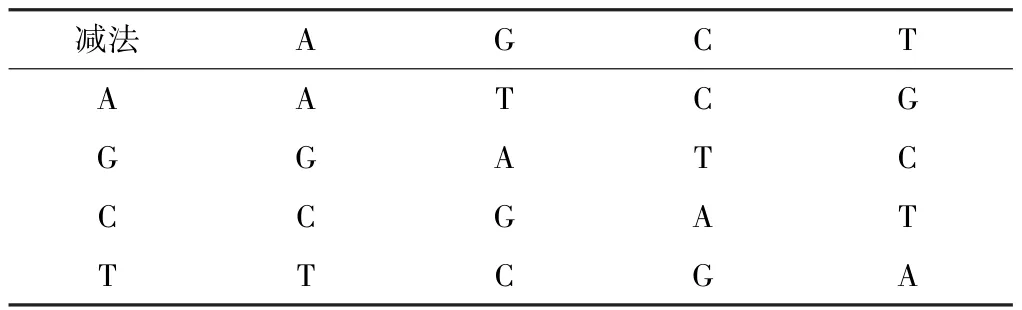
表3 DNA減法

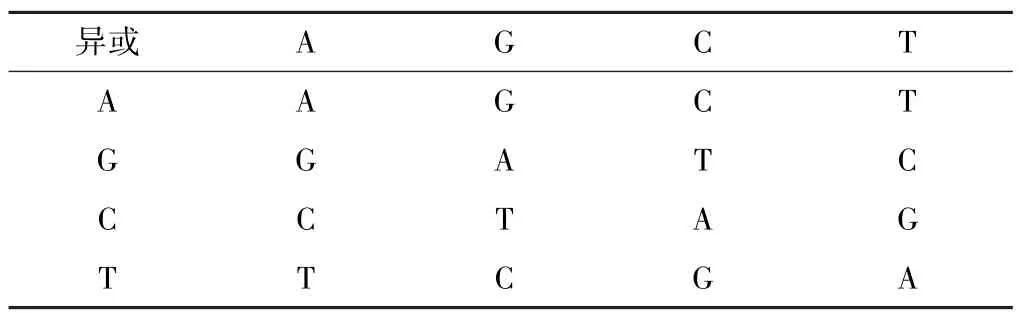
表4 DNA異或

2 加密過程與加密算法

本次加密算法使用真彩圖像進行實驗,先利用RGB轉CIE L*a*b*色彩空間原理將原圖轉換至該色彩空間,然后在Matlab中使用函數使其變為灰度圖像,再做進一步操作。加密過程如圖2所示。

文中對圖像加密分為4部分:

步驟1 根據RGB圖像至CIE L*a*b*色彩空間的原理和兩步轉換規則,轉換輸入的RGB圖像I0的色彩空間,并將圖像降至二維,分別得到CIE L*a*b*色彩空間下的圖像I1和降維后圖像I2。

步驟2 根據超混沌Chen系統生成4個混沌(8bit)序列,應用于后續DNA編碼置換的過程。

步驟3 根據二維Logistic混沌映射規則,對I2圖像進行擴散置亂,得到圖像E1,再根據廣義Arnold混沌映射規則,對E1圖像進行操作得到圖像E2。

步驟4 利用步驟2獲得的X＇,Y,Z,H4個混沌序列,結合DNA編碼規則將圖像的每個像素點進行對應轉換,對圖像E2進行置亂操作,得到最終加密圖像E3。詳細加密流程圖如圖3所示。

加密流程具體步驟如下:

輸入真彩圖像I0,參數初值

輸出加密圖像E3

步驟1 將真彩圖像I0進行色彩空間的轉換,得到CIE L*a*b*色彩空間的圖像I1。

步驟2 將步驟1得到的圖像I1通過降維函數將其改變為灰度圖像I,并將圖像矩陣I轉換成大小為M×N的二維矩陣I2。

步驟3 將圖像I2分解為4個相等大小子塊,編號依次為Ti(i∈[1,4]),并將圖像的行列數都補成可以被4整除的數。由于4塊的加密方法均相同,加密方法中混沌序列加密過程僅根據其中1塊進行說明,另外3塊加密方式類似。

步驟4 根據Chen系統所需的4個初值參數,采用ody45的方法和微分方程進行求解,輸入超混沌Chen系統的初始值x,y,z,ω,生成4個混沌(8bit)序列X＇,Y,Z,H,將應用于后續DNA編碼置換的過程。

步驟5 初始化Logistic映射控制參數:μ=4,λ1=0.9、λ2=0.9、γ=0.1,根據二維 Logistic公式進行迭代映射,得到圖像序列I3和加密圖像E1。

步驟6 廣義 Arnold變換矩陣的形式為A=[1,p;q,1+p·q];按照輸入的密鑰p,q構建廣義Arnold變換矩陣A,將輸入的圖像E1在A的作用下進行迭代置亂加密得到密文圖像E2,并得到圖像序列I4。

步驟7 根據步驟4獲得的X＇,Y,Z,H,取其前8MN項,并不重復地對T1,T2,T3,T4依次將連續8個比特數進行比特合并,得到4個長度為MN的隨機序列,分別記為K1,K2,K3,K4。接著,令Q=K1⊕K2⊕K3⊕K4。對于I4中的第i(i=1,2,…,MN)個像素點,構建公式:

可以得出,A、B、C、D∈(1,2,3,…,8),又根據DNA序列編碼和其運算規則,按照規則A,將密文圖像E2中的T1部分圖像塊進行DNA編碼,按照規則B,將T2部分圖像塊進行編碼,按規則C,將T3部分圖像塊進行編碼,按規則D,將T4部分圖像塊進行編碼;然后對對應的圖像塊根據編碼規則進行DNA運算操作;將運算結果再進行上一步驟的運算,成為擴散過程。最后將分別加密的圖像塊按照原始的分塊方式進行拼接,合并成完整的最終加密圖像E3。

解密為加密的逆向流程。在文中不做詳細說明。

3 仿真測試

3.1 測試環境

本次使用Windows10,內存16G,CPU為Inter i5的電腦配置進行實驗,測試平臺為Matlab 2018a。作為對比,選用Lena圖(256×256像素)進行測試。該算法的仿真測試從密鑰空間、灰度直方圖、相關系數、差分攻擊、信息熵等5個方面來進行,從而得出本文算法是否具有足夠高的安全性。圖4為本文算法測試的真彩Lena明文圖像和加密后的密文圖像。圖5為本文加密圖像的解密結果。無法簡單用肉眼分辨解密后圖像和加密前原圖的差異,基本判定該算法能夠將圖像信息進行加密傳遞,并讓接收者也能夠順利解密獲得該圖像信息。

3.2 密鑰空間分析

如果要讓加密的效果達到最好,也就是能夠接受多種密鑰的攻擊,需要足夠大的密鑰空間。研究數據顯示:當整個算法的密鑰空間達到2100時才能夠說加密圖像的安全性達到了可以保障的程度[18]。本次使用了64位的CPU,假設計算機浮點數的計算精度可以達到10-14,則整個加密算法的密鑰空間可以達到(1014)5=1070。經過計算,所要求的2100≈1.27×1030,1070遠大于2100,故滿足要求。因此,可以得出初步結論:這種加密方式有足夠大的密鑰空間,能夠有效地抵御絕大部分的物理攻擊。

3.3 灰度直方圖分析

灰度直方圖是將數字圖像中的所有像素,按照灰度值的大小,統計其出現的頻率。灰度直方圖是灰度級的函數,表示圖像中具有某種灰度級的像素的個數,反映圖像中某種灰度出現的頻率[19]。一個理想的加密算法應該使任何灰度圖像在加密之后得到的密文圖像中盡可能少地呈現出明顯的特征,即灰度直方圖在加密后呈現均勻分布。密文直方圖的分布越均勻,說明該加密算法就越安全[20]。圖6是該算法應用到Lena圖前后灰度直方圖的對比,可以看出:加密之后的灰度直方圖分布均勻,說明加密后的圖像不具有任何對解密有用的明顯信息,證明加密系統有效且安全性高。

3.4 相關系數分析

一般情況下,一張未加密的、完整的圖像相鄰像素之間的相關性較高,可以達到90%及以上。為防止攻擊者對圖像進行統計分析,需要降低圖片相鄰像素的相關性。本次實驗隨機選取原始圖像和加密圖像上5000對相鄰像素點(水平、垂直、對角方向),并計算像素間的相關性。

其中:x,y分別代表圖像中相鄰像素的橫、縱方向灰度值;cov(x,y)代表協方差;D(x)和E(x)分別代表方差和平均值。表5給出了原始圖像和加密后圖像在水平方向、垂直方向、對角方向相鄰像素的相關性。并與文獻[21-22]比較,以表現本文算法的安全性之高。

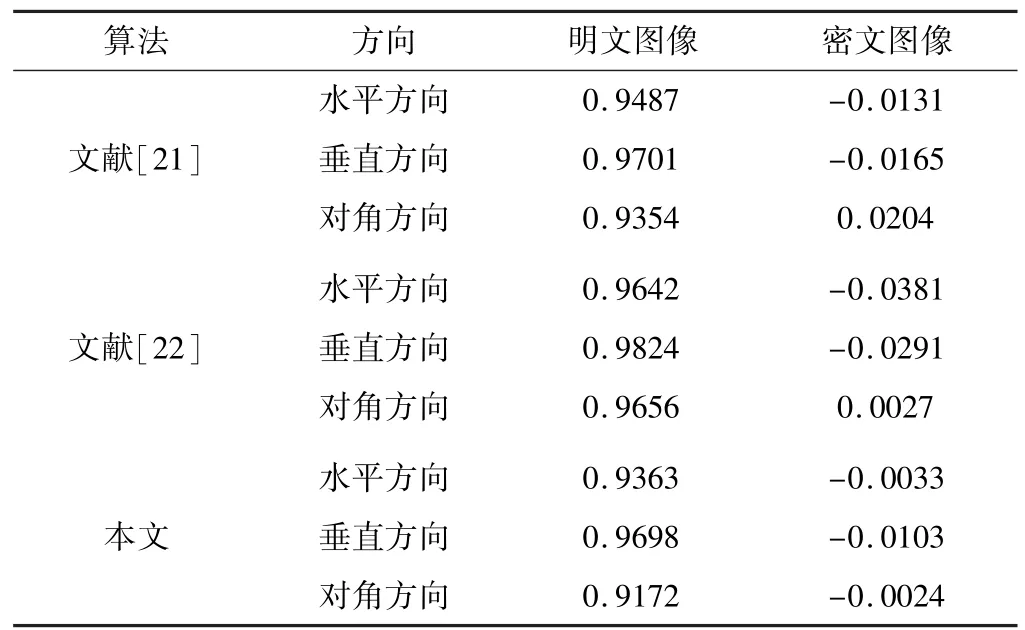
表5 相關系數測試結果

由表5可知,當明文圖像的相關系數均非常接近于1,同時加密圖像的相關系數均非常接近于0時,就表明明文圖像的相鄰像素點之間具有較強的相關性,而加密圖像的相鄰像素點之間基本不具備相關性[23]。圖7和圖8分別為Lena灰度圖加密前后的相鄰像素點在水平方向、垂直方向和對角方向的相關性散點相圖。

3.5 差分攻擊分析

本文的加密算法,使用的密鑰和明文圖像相關,使得明文圖像對密文圖像非常敏感,故只要稍微修改一點明文圖像的像素值就會使密文圖像大相徑庭,從而保證加密算法的安全性。這里,假設明文圖像為I,則H,W分別為明文圖像的長與寬,C1為加密圖像,通過將I中某一個像素值進行微調(將像素值加1bit或減1bit),得到調整后的加密圖像C2。引入兩個相關概念,分別是像素改變率(number of pixels change rate,NPCR)和歸一化平均變化強度(unified average changing,UACI)。

其中,C1(i,j)和C2(i,j)分別代表明文圖像像素值被微調之前后所對應的密文像素值。NPCR的值越接近100%,或UACI的值越接近33%,此時的加密算法處理后的加密圖像敏感性越高,抵抗差分攻擊的能力越強。表6是本文算法與文獻[8,21,25]的算法比較,可以看出,本文算法處理圖像能夠有效抵御差分攻擊。

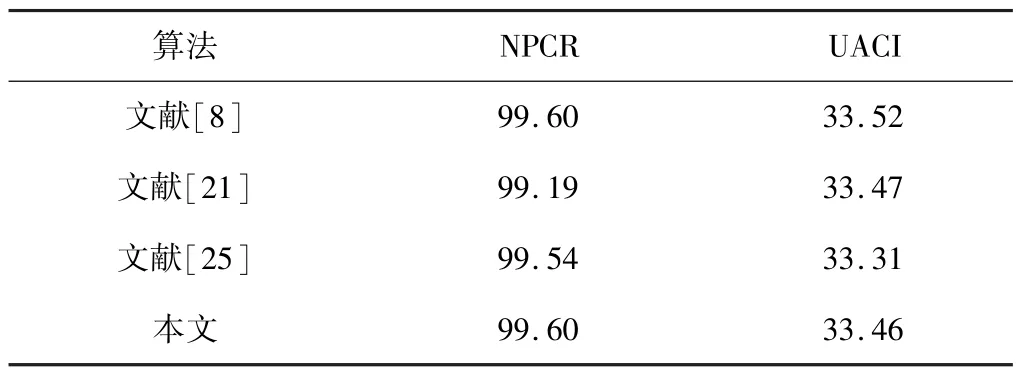
表6 NPCR/UACI測試結果 單位:%

3.6 信息熵

1948年,香農提出了“信息熵”的概念,為解決信息量化的問題。信息熵被定義為描述系統的不確定性的程度,可以用來表示圖像信息的不確定性。計算公式如下:

其中,p(mi)表示某信息mi出現的概率。根據實驗數據知,信息熵越大,越接近完全隨機的圖像信息熵8,則該加密圖像的灰度值分布越均勻、隨機性越大、信息傳遞越安全。表7為本文算法和文獻[8,25,27]的算法加密圖像后的信息熵測試結果。

表7 加密圖像信息熵

與其他算法比較,可以看出本文算法得到一個較大的信息熵值,非常接近理想值。這表明該加密圖像發生信息泄露的可能性極小,也間接證明了加密算法的安全性。

4 結束語

提出了一種將DNA編碼規則和超混沌系統相結合的圖像加密算法。通過轉化圖像色彩空間、降低圖像維度;利用Chen超混沌系統、二維Logistic系統、廣義Arnold系統和DNA編碼序列的多重運算來達到安全高效加密明文圖像,實現圖像置亂和像素值擴散過程。先轉換圖像顏色空間,再分別通過Chen超混沌系統、二維Logistic映射和廣義Arnold映射組成的超混沌系統對圖像像素值進行擴散、置亂操作,最后結合DNA編碼規則對處理后的圖像再次置亂加密,得到最終的密文圖像。本文經過密文圖像密鑰空間、灰度直方圖、相關系數、差分攻擊和信息熵值等測試方法,從多方面專業化地驗證了該算法處理后的加密圖像的安全性。下一步將研究深度學習和基于DNA序列卷積神經網絡的圖像加密算法。計劃針對深度學習中的LSTM神經網絡,通過預測時間序列,生成預測新混沌信號,并使用Pytorch等工具進行混沌序列的訓練,得到新混沌信號,再結合多維混沌系統和DNA編碼,能夠更進一步提升圖像加密的安全性。

致謝:感謝大學生創新創業訓練計劃項目(202010621260)對本文的資助。