基于GeoGebra的楊氏雙縫實驗動態模擬

鄭潤楠 姜玉梅

(揚州大學物理科學與技術學院 江蘇 揚州 225000)

蘇俊

(江蘇省海安高級中學 江蘇 南通 226600;華東師范大學教師教育學院 上海 200062)

1801年英國物理學家托馬斯·楊(Thomas Young)的雙縫干涉實驗，為光的波動學說提供了堅實的實驗證據支撐，被美國《物理世界》雜志評選為“最美”的十大物理實驗之一[1].楊氏雙縫實驗不僅被《普通高中物理課程標準》規定為學生必做實驗，也是高校光學、大學物理實驗等課程的重要內容.

近年來，國內學者對楊氏雙縫實驗的仿真研究數量頗多，比較常用的軟件工具有MATLAB，Mathematica，Labview等[2～4]，均能較好地實現參數可調節和實驗現象對應呈現等功能.然而，在課堂教學過程中運行此類大型應用程序并不方便，且現有研究主要側重于對楊氏雙縫實驗現象的模擬，對干涉原理的模擬則與常見教科書在介紹雙縫實驗原理時的配圖類似，都是基于惠更斯原理描繪出各個波陣面，并將其與干涉圖樣在同一平面內呈現，如圖1所示.

圖1 教科書中關于雙縫實驗的常見配圖

然而，惠更斯原理無法準確解釋波的干涉現象[5].并且，靜態圖無法體現波的傳播過程，平面圖也難以同時呈現波的疊加與分布，導致部分空間思維能力欠佳的學生在理解該實驗時存在一定困難[6].因此，本文運用GeoGebra軟件的3D繪圖功能，開發了一個三維動態模擬楊氏雙縫實驗的程序，可作為物理教學的輔助，降低學生的認知負荷，幫助學生更好地理解干涉原理與現象.

1 楊氏雙縫實驗的干涉原理

楊氏雙縫干涉是一種典型的雙光束干涉.如圖2所示，兩光源S1和S2的距離為d，光源所在平面與屏幕平行，兩者之間的垂直距離為D，在屏幕上任取一點P，它與S1和S2的距離分別為r1和r2.

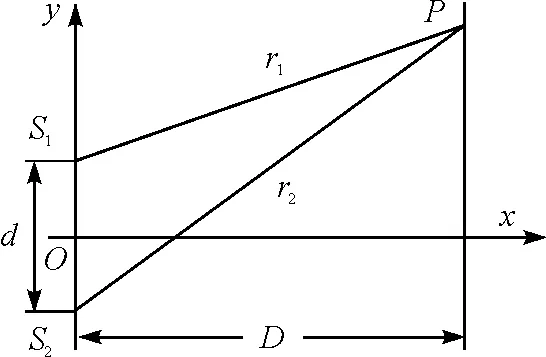
圖2 楊氏雙縫實驗示意圖

兩光源S1和S2的振動方向相同，圓頻率為ω，振幅大小分別為A1和A2，初相位分別為φ1和φ2，則S1和S2兩點的光振動方程分別為

E10=A1cosωt+φ1

(1)

E20=A2cosωt+φ2

(2)

E10=A1cosk1v1t+φ1

(3)

E20=A2cosk2v2t+φ2

(4)

t時刻，從S1和S2發出的兩列波引起P點的光振動分別是

E1=A1cosφ1-k1r1-v1t

(5)

E2=A2cosφ2-k2r2-v2t

(6)

P點處的合振幅為

(7)

P點處的光強為

(8)

其中

Δφ=φ2-φ1-k2r2-k1r1

(9)

當Δφ=±2jπ，j=0,1,2,… 時，干涉相長，光強最大.

當Δφ=±2j+1π，j=0,1,2,…時，干涉相消，光強最小.

楊氏雙縫實驗的裝置通常放在空氣中，因此有k1=k2=k，Δφ=φ2-φ1-kr2-r1，在D?d條件下，光學教科書常通過r2-r1≈dsinθ，sinθ≈tanθ兩次近似，得到干涉的規律，而沒有對近似條件之外的情況進行詳細探討.近似處理雖便于學生掌握，但會給定量研究引入一些誤差，利用幾何關系式(10)、(11)求出實際的幾何路程則可避免這一誤差.

(10)

(11)

2 楊氏雙縫實驗動態模擬程序的開發

GeoGebra是一款免費、開源、兼容性高的動態數學軟件，近年來將其用于輔助中學物理教學的研究熱度較高，其動態演示功能可以幫助學生更直觀地理解物理概念與規律.由于它還是一款漸進式網頁應用(PWA)，因此教師可直接在課堂上用瀏覽器打開鏈接進行演示，十分便捷.本節將對運用GeoGebra軟件開發此模擬演示程序時的主要思路與步驟進行介紹.

第一步定義物理量：首先，打開GeoGebra的3D繪圖區和默認繪圖區，調整合適的界面格局；然后，運用“描點”工具在3D繪圖區的y軸上取一點，命名為S1，使用“定長線段”工具設置在y軸上與點S1距離為d的點S2.接著，在與y軸距離為D處繪制一條平行于y軸的直線，在直線上取一點P，連接PS1和PS2，連線與x軸方向的夾角分別設為α1和α2；最后，在默認繪圖區中創建對應物理量的“滑動條”.

第二步輸入方程：為了演示波的傳播過程，首先輸入從兩光源S1和S2發出光波的波動方程.以光傳播距離在x軸方向上的投影為自變量X，t時刻，在S1P方向上與S1相距l1的一點P1(xP1,yP1)處產生的光振動為

EP1=A1cosφ1-k1l1-v1t

(12)

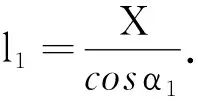
同理，S2在與其相距l2的一點P2(xP2,yP2)處產生的振動為

EP2=A2cosφ2-k2l2-v2t

(13)

且由于P1是線段PS1上的一點，因此，有

(14)

同理，對P2，有

(15)

在GeoGebra的“代數區”中輸入相應代碼，如圖3所示，即得到兩列波的圖樣，為了模擬波形隨時間的推進，此處還定義了自變量隨時間變化的取值范圍.

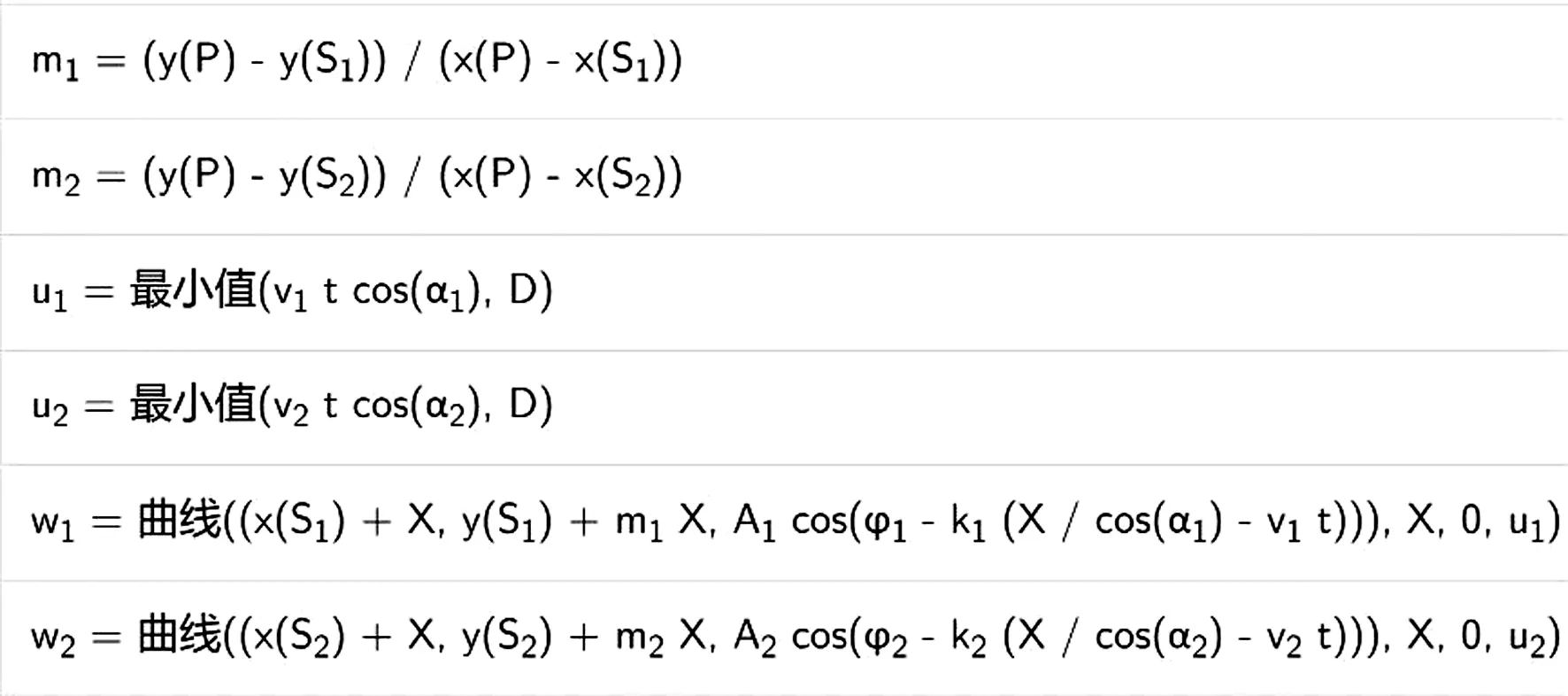
圖3 部分程序代碼

之后輸入不含近似處理的合振幅分布函數式(7)與光強分布函數式(8)等的代碼，可得到合振幅分布曲線以及光強分布曲線等圖樣.

第三步為功能拓展與完善：首先，由于楊氏雙縫實驗要求兩束光為相干光，所以在程序中設置了一個“同步”的功能，可以通過點擊“同步”按鈕將S1和S2的角波數、波速、初相位快速進行統一；之后，為了更直觀地呈現“干涉相消”和“干涉相長”現象，通過波動方程模擬出兩列波到達P點之后的延續狀態以及疊加后的波形；最后，為了讓學生更直觀地體會光程差對疊加效果的影響，尤其是當φ2=φ1時，光程差的作用效果，基于“折射率n=1時，光程差等于幾何路程差”的結論，以P點為圓心、以r1和r2兩者中的較小者為半徑，用虛線繪制了一個輔助圓，并用對比色突現出幾何路程差值部分的波形，加以復選框功能讓用戶自行選擇是否顯示相關內容.最終模擬程序的界面及其鏈接二維碼如圖4所示.

(a)

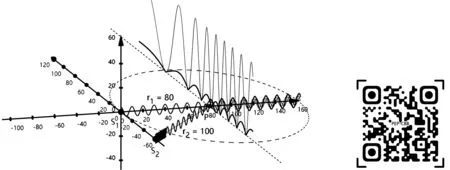
(b)

3 楊氏雙縫實驗動態模擬程序的演示

3.1 光波的傳播與疊加

此程序可向學生動態展示從S1和S2發出的兩列波的傳播過程以及在P點疊加的任意情況，尤其是在P點發生干涉相長和干涉相消的情況.例如：在λ1=λ2=10參數條件下的兩列相干波，當光程差恰好等于一個波長時，如圖5(a)所示，則合振幅最大，光強最大；而當光程差恰好等于半個波長時，如圖5(b)所示，則兩列波相互抵消，合振幅最小，光強最小.

運用GeoGebra進行動態模擬演示，可將抽象的干涉規律形象化，調動學生的視覺直觀功能，從而加深學生對干涉現象及干涉條件的理解.

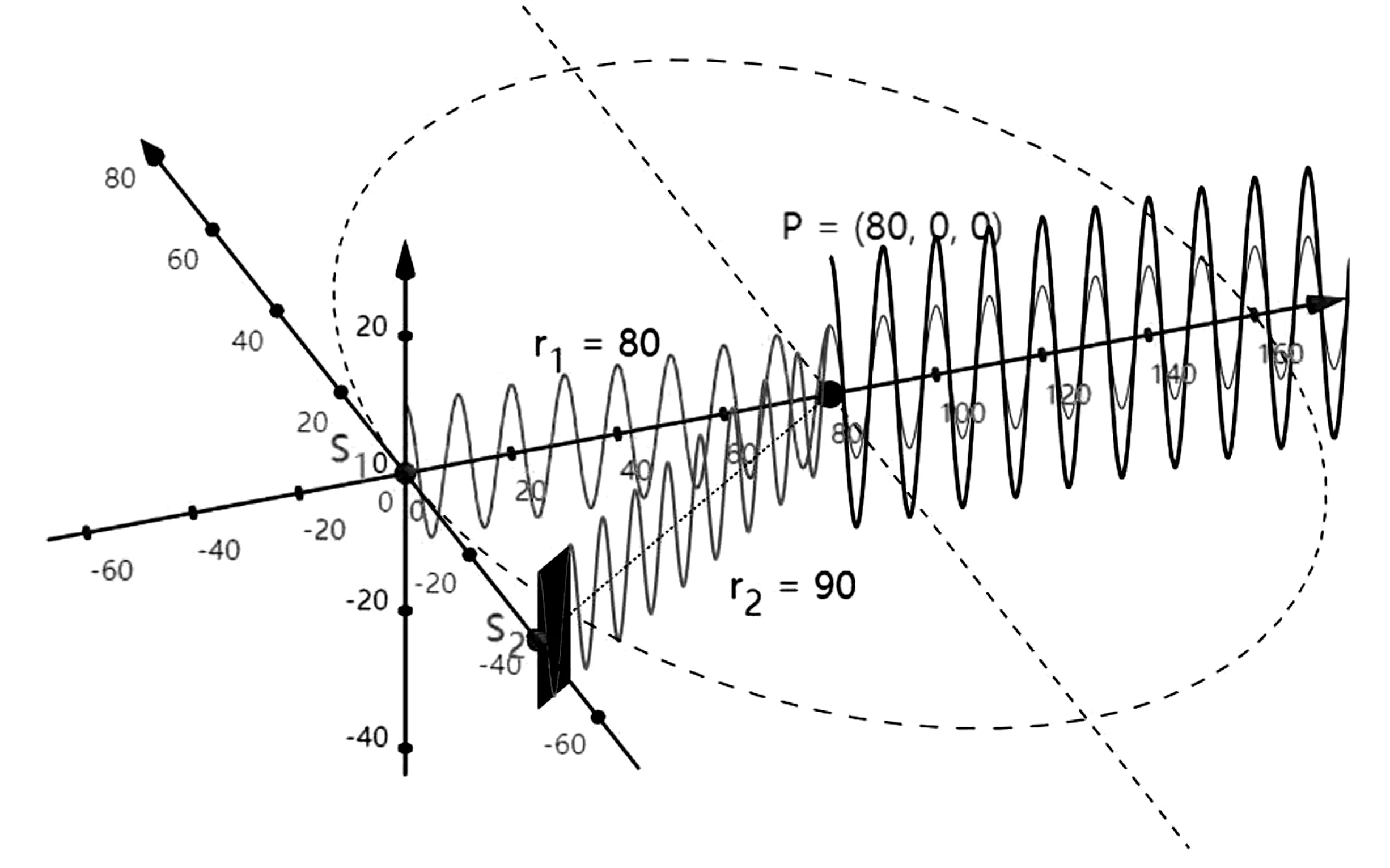
(a)楊氏雙縫實驗干涉相長的動態模擬

(b)楊氏雙縫實驗干涉相消的動態模擬

3.2 不同參數下的干涉圖樣

學生對光波波長λ,雙縫間距d,光屏與雙縫距離D這些參數對干涉圖樣影響的認識，僅局限于在近似條件下干涉圖樣相鄰明(暗)條紋的間距Δx與上述參數間的定量關系式

(16)

由于缺乏形象感知，大部分學生對此公式只能死記硬背，更不了解不同參數對干涉圖樣強度的影響.而GeoGebra可以將這些參數對干涉強度和干涉條紋間距的影響可視化，有助于學生靈活把握此類公式，加深對楊氏雙縫實驗的理解.

例如，分別設置λ,d,D對應滑動條的播放速度，可以直觀地演示干涉圖樣隨單一參數的動態變化，從而讓學生感知相鄰明(暗)條紋間距Δx與λ,d,D3個參數之間的定性關系，如圖6所示.

而通過調節“全局設置”中的“精確度”，還可運用GeoGebra直接測出干涉圖樣相鄰明(暗)條紋的間距Δx.如圖7所示，設置精確度為“保留10位小數”，輸入參數λ=640 nm，d=0.4 mm，D=50 cm，可計算出相鄰兩暗條紋的間距，即B,C兩點的距離，所得結果與運用近似公式(16)計算的結果差異極小，表明GeoGebra也可用于開展物理定量研究.

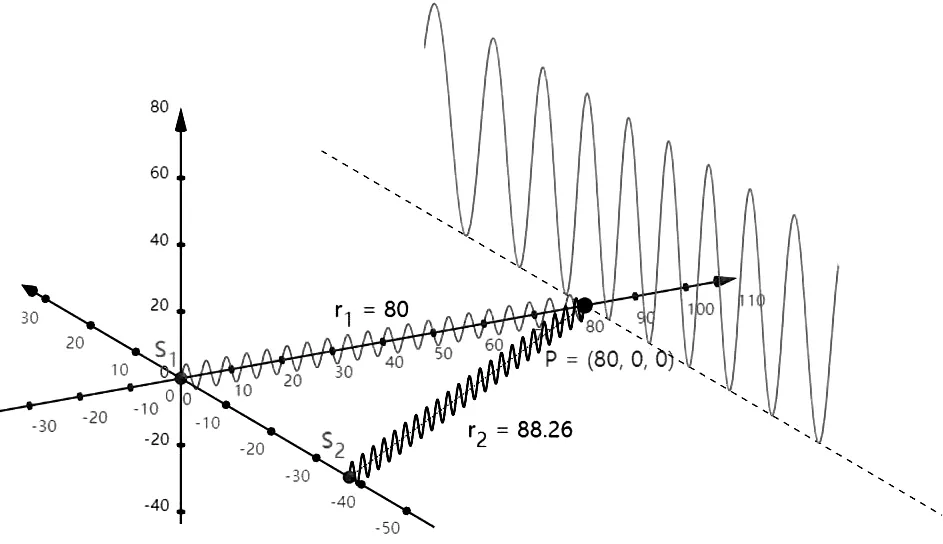
圖6 楊氏雙縫實驗光強分布的動態模擬

圖7 運用GeoGebra測量相鄰暗條紋的間距

4 結束語

本文運用GeoGebra軟件的3D繪圖功能，開發了一個動態模擬楊氏雙縫實驗的程序，能夠實現干涉過程的可視化，直觀地揭示出干涉現象的成因，還能用于定性和定量地研究干涉條紋、光強分布與光波波長λ,雙縫間距d和光屏與雙縫距離D的關系，輔助楊氏雙縫實驗的教學.并且，由于此程序中幾乎所有參數都可自行設置，因此,除了用于模擬相干波的疊加，還可用于研究其他非相干波的疊加.GeoGebra程序的源代碼都是開放的，教師可根據教學與研究的需要對本文所設計程序進行更深入的拓展與應用.