基于“一題多解”促核心素養(yǎng)發(fā)展
馬淑紅 焦照勇 賈光瑞
(河南師范大學(xué)物理學(xué)院 河南 新鄉(xiāng) 453007)
1 引言
點(diǎn)的合成運(yùn)動(dòng)是理論力學(xué)課程教學(xué)的重難點(diǎn)內(nèi)容之一[1],許多實(shí)際問(wèn)題涉及的主要是做一般運(yùn)動(dòng)的剛體系統(tǒng),求解這類復(fù)雜運(yùn)動(dòng)問(wèn)題需要正確分析運(yùn)動(dòng)間關(guān)聯(lián)和運(yùn)動(dòng)形式,恰當(dāng)選取體(動(dòng))坐標(biāo)系,以及靈活運(yùn)用力學(xué)知識(shí)和方法.許多學(xué)生在解決問(wèn)題時(shí)主要運(yùn)用基點(diǎn)法公式,解題方法單一死板,形成了思維定式.當(dāng)遇到復(fù)雜運(yùn)動(dòng)問(wèn)題時(shí),學(xué)生會(huì)感到困惑、迷思、無(wú)從下手,不利于發(fā)散思維和創(chuàng)新思維的發(fā)展[4].本文基于教學(xué)實(shí)踐,以教材中飛機(jī)上螺旋槳運(yùn)動(dòng)的典型問(wèn)題為例[1],通過(guò)“一題多解”多途徑探究[2~4],展示和探討它對(duì)促進(jìn)學(xué)生整合知識(shí)、優(yōu)化方法,靈活運(yùn)用、融會(huì)貫通和物理核心素養(yǎng)發(fā)展的作用和重要性.
2 一題多解
【例題】當(dāng)飛機(jī)在空中以一定值速度u沿半徑為R的水平圓形軌道O轉(zhuǎn)彎時(shí),求當(dāng)螺旋槳尖端B與中心A的連線和豎直線成θ角時(shí),B點(diǎn)的速度vB及加速度aB.已知螺旋槳的長(zhǎng)度AB=l,螺旋槳自身旋轉(zhuǎn)的角速度為ω1.
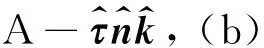

(a)
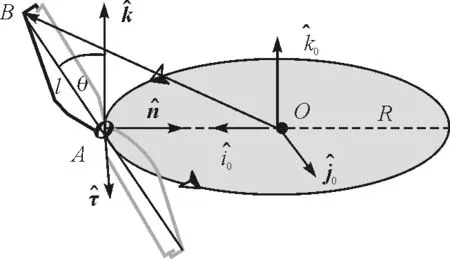
(b)
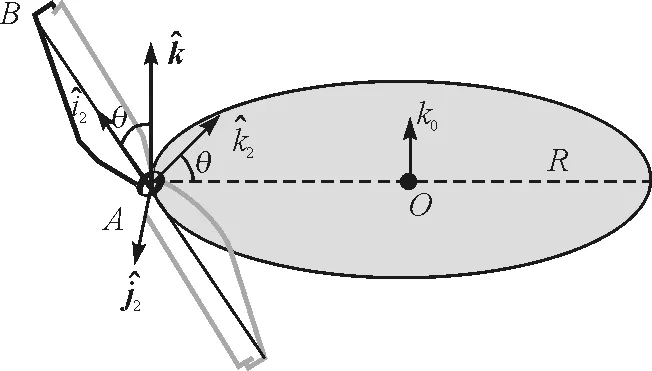
(c)
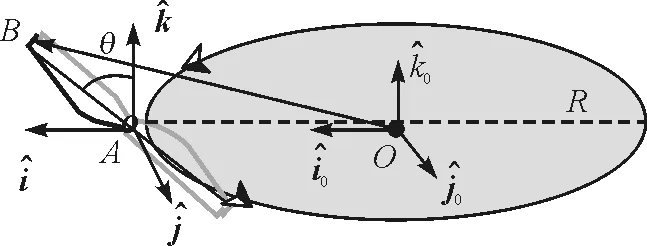
(d)
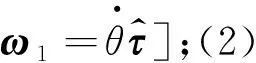

(1)
解法1:自然坐標(biāo)系絕對(duì)位矢求導(dǎo)法.
如圖1(b)所示,螺旋槳尖端點(diǎn)B相對(duì)于固定點(diǎn)O的絕對(duì)位矢
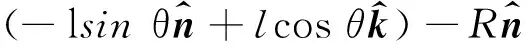
(2)
對(duì)式(2)兩邊求時(shí)間的瞬時(shí)變化率,得到點(diǎn)B的速度
(3)
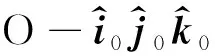
(4)
類似地,對(duì)式(4)兩邊求時(shí)間的瞬時(shí)變化率,并應(yīng)用式(1),可得點(diǎn)B絕對(duì)加速度
(5)
上述解法是從動(dòng)點(diǎn)的絕對(duì)位矢出發(fā),基于運(yùn)動(dòng)學(xué)量關(guān)系,通過(guò)求矢量對(duì)時(shí)間的瞬時(shí)變化率,得出動(dòng)點(diǎn)的速度和加速度.該解題方法思路簡(jiǎn)單,關(guān)鍵在于求動(dòng)系單位矢量瞬時(shí)變化率.
解法2:剛體運(yùn)動(dòng)基點(diǎn)法.
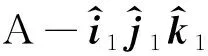
(6)

(7)
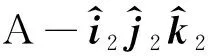
運(yùn)用剛體基點(diǎn)公式
可得結(jié)果式(8)
(8)
綜上,由于坐標(biāo)軸選取不同,該結(jié)果與解法1結(jié)果表示形式有別;解法2中建立的剛體體坐標(biāo)系更直觀明了,其關(guān)鍵是確定剛體繞基點(diǎn)瞬軸轉(zhuǎn)動(dòng)運(yùn)動(dòng)狀態(tài).
解法3:點(diǎn)的合成運(yùn)動(dòng)法.
由點(diǎn)的合成運(yùn)動(dòng)理論:動(dòng)點(diǎn)B相對(duì)于靜系的絕對(duì)運(yùn)動(dòng)(vB、aB)等于其相對(duì)動(dòng)系的相對(duì)運(yùn)動(dòng)(vr、ar)與動(dòng)系相對(duì)于靜系的牽連運(yùn)動(dòng)兩者的疊加,即
(9)

動(dòng)點(diǎn)對(duì)動(dòng)系的相對(duì)運(yùn)動(dòng):螺旋槳尖端動(dòng)點(diǎn)B相對(duì)動(dòng)系原點(diǎn)A的相對(duì)位矢、相對(duì)速度和相對(duì)加速度分別為
(10)
經(jīng)上述分析計(jì)算,可得動(dòng)點(diǎn)B對(duì)靜系的絕對(duì)速度和加速度.
類似地,若建立以螺旋槳中心點(diǎn)A為原點(diǎn)的動(dòng)坐標(biāo)系[如圖2(b)],則點(diǎn)B相對(duì)動(dòng)系靜止(ar和vr等于零),解法3回歸到解法2.
該方法的關(guān)鍵是動(dòng)系的建立和相對(duì)運(yùn)動(dòng)分析[5],這里分別以機(jī)身和螺旋槳?jiǎng)酉禐槔罨瘜W(xué)生對(duì)知識(shí)理解,加強(qiáng)學(xué)生靈活運(yùn)用和掌握解題方法.
3 解法討論及對(duì)學(xué)生創(chuàng)造性思維等核心素養(yǎng)的培養(yǎng)
比較上述解法不難發(fā)現(xiàn):
(1)剛體基點(diǎn)公式法僅適用于固結(jié)于剛體上的點(diǎn)的運(yùn)動(dòng),其余兩種方法在求解任意動(dòng)點(diǎn)的復(fù)雜運(yùn)動(dòng)問(wèn)題時(shí)更具普適性.
(2)絕對(duì)位矢求導(dǎo)法是最基礎(chǔ)的解法,基于動(dòng)點(diǎn)的絕對(duì)位矢,運(yùn)用求導(dǎo)運(yùn)算推導(dǎo)出動(dòng)點(diǎn)的速度和加速度,推理過(guò)程簡(jiǎn)單,學(xué)生都能熟練掌握.該方法有助于培養(yǎng)學(xué)生科學(xué)的邏輯思維方法和嚴(yán)謹(jǐn)?shù)耐评砟芰Γ瑥?qiáng)化求導(dǎo)微分物理思想的滲透,具有與其他方法異曲同工之妙.
(3)點(diǎn)的合成運(yùn)動(dòng)法是基于運(yùn)動(dòng)疊加原理來(lái)描述點(diǎn)的復(fù)雜運(yùn)動(dòng),其運(yùn)動(dòng)變換關(guān)系為

歸結(jié)為“一點(diǎn)、二系、三運(yùn)動(dòng)”,其解題思路清晰,學(xué)生易形成解題程序性范式,其關(guān)鍵是正確分析各種運(yùn)動(dòng),是一種普適解法.
上述3種解題方法和思路從不同的觀點(diǎn)出發(fā),能夠開闊學(xué)生眼界和思路,促使學(xué)生對(duì)所學(xué)理論知識(shí)進(jìn)行整合和重構(gòu),貫通各章節(jié)碎片化的知識(shí)以達(dá)到靈活運(yùn)用,啟迪創(chuàng)新思維,培養(yǎng)學(xué)生多途徑解決問(wèn)題的能力.通過(guò)一題多解對(duì)問(wèn)題進(jìn)行反思,多問(wèn)多想為什么,弄清物理本質(zhì),站在物理觀念的角度,運(yùn)用科學(xué)思維和深入分析探究的科學(xué)方法,培養(yǎng)學(xué)生的發(fā)散性和創(chuàng)造性思維,促進(jìn)核心素養(yǎng)發(fā)展.
4 結(jié)論
本文運(yùn)用絕對(duì)位矢求導(dǎo)法、剛體基點(diǎn)公式法、點(diǎn)的合成運(yùn)動(dòng)法一題多解“飛機(jī)上螺旋槳的運(yùn)動(dòng)”問(wèn)題,討論了各解法的關(guān)鍵和坐標(biāo)系選取的影響.旨在通過(guò)“一題多解”強(qiáng)化學(xué)生對(duì)所學(xué)理論的融會(huì)貫通和解題方法的靈活運(yùn)用,提高學(xué)生解決問(wèn)題的能力,促進(jìn)學(xué)生創(chuàng)新思維能力的發(fā)展.
它能促進(jìn)學(xué)生整合知識(shí)、優(yōu)化方法,靈活運(yùn)用、觸類旁通、融會(huì)貫通的教學(xué)效果,提高學(xué)生解決問(wèn)題的能力,激發(fā)學(xué)習(xí)物理的積極主動(dòng)性和創(chuàng)造性思維,促進(jìn)核心素養(yǎng)發(fā)展.

