基于Phyphox和Origin的簡易實驗設計
——定量探究向心加速度公式
李雨茜 黃澤璇 鄧浩儀 張軍朋
(華南師范大學物理與電信工程學院 廣東 廣州 510006)
1 問題的提出
對于向心加速度公式的教學,已有研究均是通過設計自制教具對向心加速度公式進行定量探究[1,2],但相關教具的制作難度大且耗時長.為此,教師可充分利用已有器材和身邊事物,結合手機傳感器設計簡易實驗以確保實驗的順利開展.此外,在向心加速度公式的得出過程中,已有研究通過a-ω散點圖呈類似拋物線的趨勢而直接給出a-ω2圖像,并通過圖像為過原點的單調遞增直線得到a與ω2成正比的結論[3,4].仔細思考此推理過程不難發現其中還有值得推敲之處:指數大于1的冪函數圖像均具有類似于拋物線的變化趨勢,為何此處只考慮平方關系?能否通過更加直接、精確的數據處理結果來說明向心加速度是與角速度的平方成正比?
基于以上原因,本文設計了定量探究向心加速度公式的簡易實驗,借助Phyphox軟件測量手機做圓周運動時a與ω的數據,并應用Origin軟件進行乘冪函數擬合,從擬合公式中冪指數的結果得到向心加速度的公式為a=ω2r,強化學生的證據意識,培養學生嚴謹的科學態度.
2 探究向心加速度公式的簡易實驗素材
為有效利用生活中可做圓周運動的物品進行探究,此處選取演示效果較好的自行車[5]、脫水菜籃、轉椅作為示例.
(1)自行車
將自行車水平放于一左一右兩張椅子上,具體擺放方式見圖1.作為測量端的手機封入透明袋中,將二者用膠帶固定在后輪上,方便拿取,防止手機脫落飛出,保持車輪可順暢轉動,此時搖動自行車腳踏即可使后輪轉動的同時帶動手機做圓周運動.

圖1 自行車橫放示意圖(俯視圖)
(2)脫水菜籃
當前市面上出現一種脫水菜籃,由上蓋、菜籃和儲水圓盒組成.使用毛巾海綿等質量較輕的雜物頂住手機使之固定于菜籃中,為避免菜籃無法平衡導致轉動不順暢,在另一端放置與手機質量相當的物品作為配重,具體放置方式如圖2.轉動上蓋的手柄即可帶動內部菜籃中的手機進行圓周運動.

圖2 用海綿將手機固定于脫水菜籃中
(3)轉椅
將生活中常見的轉椅倒放如圖3,手機固定在其中一個可自由轉動的椅腳,當撥動椅腳時可帶動手機做圓周運動.
經筆者多次實驗發現,以上3種生活器材在探究向心加速度公式時均具有很好的實驗效果,可供師生自行選擇.本文將以自行車為例,對實驗過程及數據處理環節進行詳細介紹.

圖3 手機固定于倒放轉椅的椅腳處
3 基于Phyphox軟件的實驗數據收集
德國亞琛工業大學的S.Staacks 等人開發的Phyphox軟件,可調用手機中的傳感器實現對加速度、角速度、壓力、光照強度等基本物理量的測量[6].圖4為部分傳感器位置示意圖,由于傳感器模塊的位置接近手機的幾何中心,因此,設手機的幾何中心為起點,自行車后輪的轉動中心為終點,用直尺測量二者的距離記為轉動半徑值
r=0.230 0 m

圖4 華為手機上部分傳感器位置示意圖
為實時顯示手機做圓周運動時對應的向心加速度a與角速度ω,在手機端Phyphox軟件的向心加速度模塊設置允許遠程訪問,以從電腦端控制數據的采集過程.以自行車為例,后續實驗操作步驟如下:
(1)點擊手機端的“?”開始測量,隨即從慢到快搖動自行車腳踏,使測量手機做角速度不斷變大的圓周運動.在此過程中,學生能每隔0.5 s實時觀察到手機從慢到快做圓周運動時,電腦端a-ω坐標軸上對應出現的數據點,且數據點的分布趨勢有類似拋物線的特征.
(2)當呈現出連續、完整的數據圖像時,從電腦端點擊停止測量,此時Phyphox軟件的界面即為本次實驗測量所得的a-ω散點圖,最后導出含有時間t、加速度a和角速度ω的Excel數據表格.為方便對比實驗效果,圖5為手機在3種生活物品上做圓周運動后手機端實驗數據散點圖.
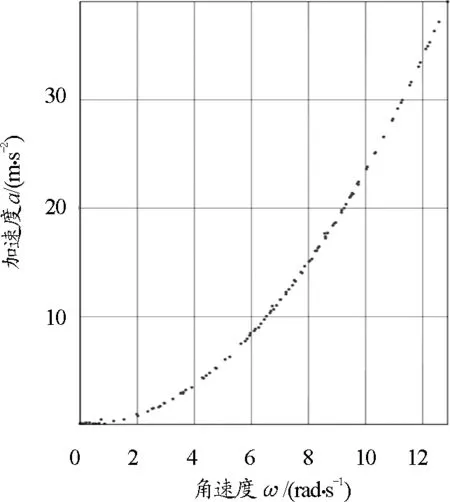
(a)自行車輪
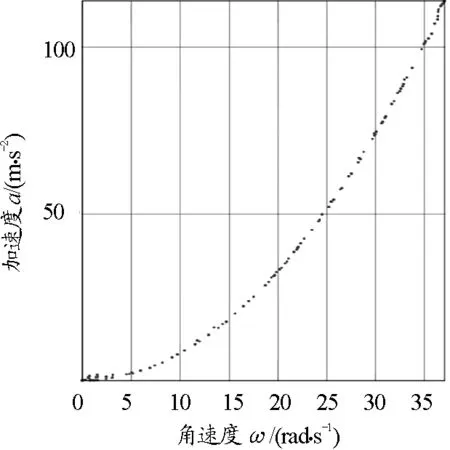
(b)脫水菜藍
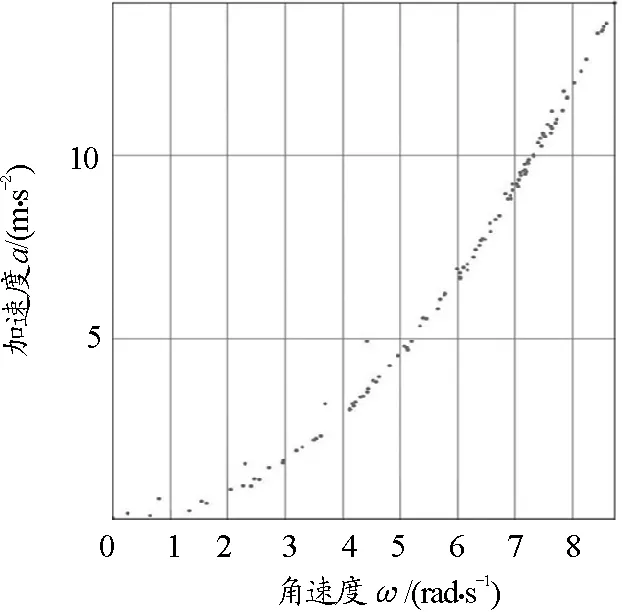
(c)轉椅
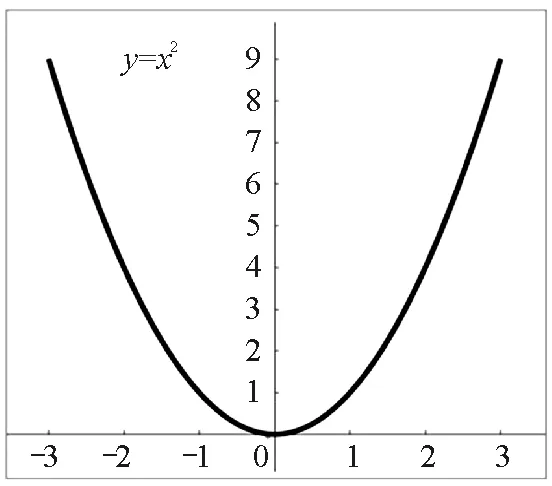
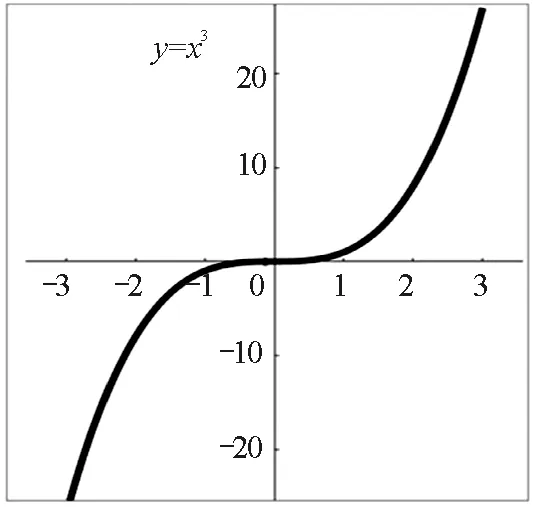
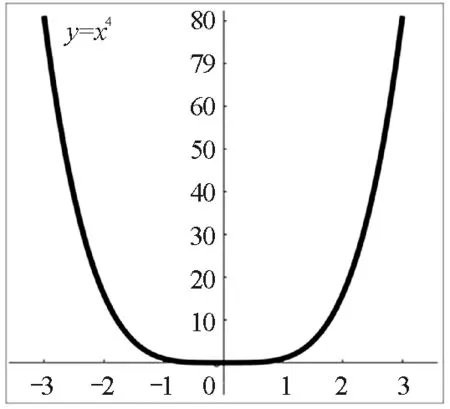
分析可知,3組數據點呈現的趨勢均是過原點在第一象限的單調遞增曲線,向心加速度隨角速度增大而增大,具有拋物線的部分特征.但僅以此趨勢不能直接判斷a與ω為二次函數關系,因為指數大于1的冪函數在第一象限都有可能出現這樣的曲線特征,如圖6所示為y=x1.5,y=x2,y=x3,y=x4等4種冪函數的圖像.此時如何確認a是與ω2成正比,而非與ω的其他次方成正比關系?為了解決這一問題,本文將應用Origin軟件進行數據擬合,應用信息技術更精確直觀地探尋二者間的關系.
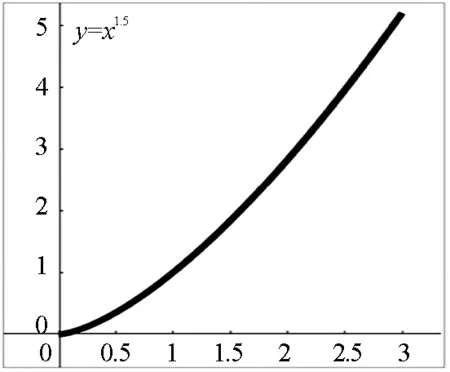
(a)
(b)
(c)
(d)
4 基于Origin軟件的實驗數據處理
Origin的強大之處在于,可直接調用函數對數據進行擬合并繪圖,尤其在非線性擬合上可以顯示更多參數,擬合結果更加準確[7].下面以手機在自行車輪上做圓周運動所收集的角速度與向心加速度數據為例,用Origin軟件進行數據處理.
(1)結合導出數據做散點圖
本次實驗共有189組的角速度ω與對應向心加速度a,表1為截選的8組數據.打開Origin軟件,將所有數據導入后點擊“散點圖”生成圖像.
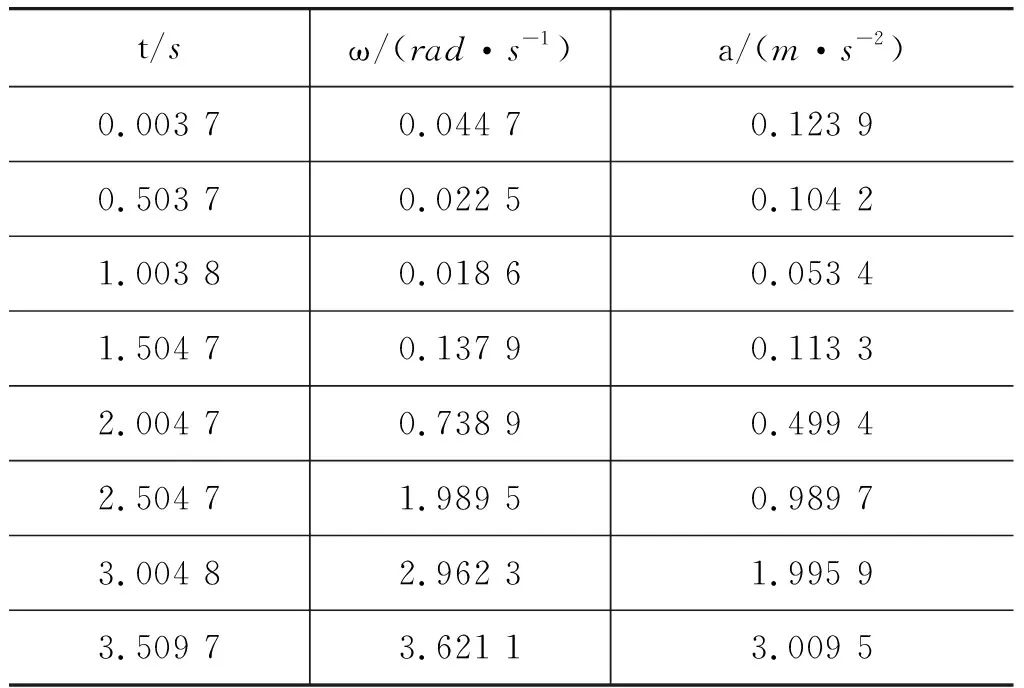
表1 手機在自行車輪上收集的角速度ω與向心加速度a數據
(2)選取數據擬合函數模型
由于a-ω散點圖明顯表現為非線性圖像,因此在Origin軟件中選擇非線性曲線擬合.根據數據點所呈現的趨勢具有乘冪函數的曲線特征,我們選擇乘冪函數模型(Allometric),以y=axb的擬合公式進行數據擬合.
(3)分析擬合公式得到結論
圖7為數據以乘冪函數擬合的結果,其中“R平方(COD)”一欄作為擬合程度的指標,其數值越接近1表示函數與實際值的擬合程度越好.本次擬合曲線的R2值高達0.999 9,代表擬合程度良好.根據擬合公式,a與ω滿足關系式
a=0.228 3ω2.011 4
(1)
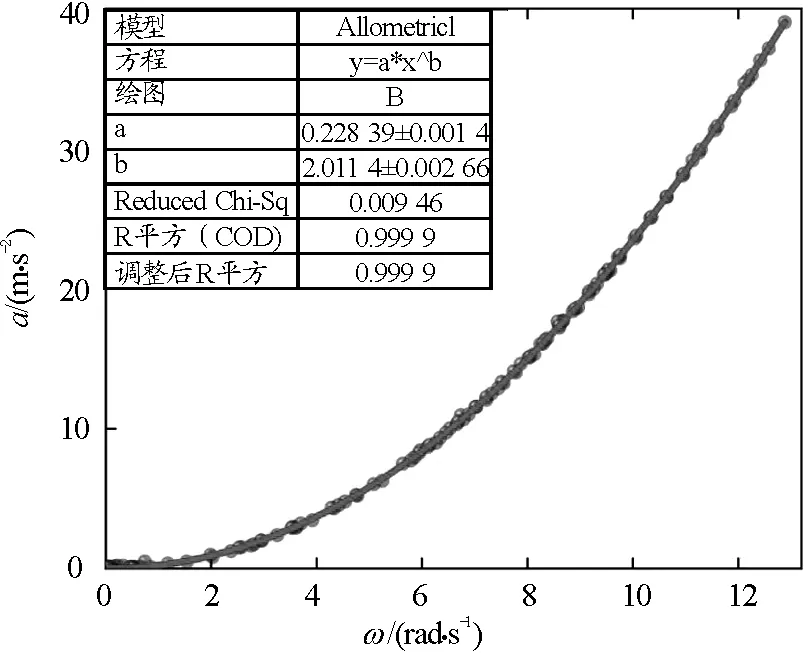
圖7 以乘冪函數模型進行擬合的結果
由式(1)可知,ω的指數為2.011 4,能更精確直觀地呈現出在誤差允許的范圍內a與ω2成正比關系.擬合公式的系數為0.228 3,對比實驗前用直尺測量的轉動半徑值r=0.230 0 m,二者誤差僅為0.739 1%.可見,本次定量探究的數據顯示向心加速度、角速度與轉動半徑三者的關系滿足a=ω2r.用相同方法處理手機在脫水菜籃、轉椅上做圓周運動時的數據結果,均可得到此結論.
5 結束語
相比于自制教具,結合Phyphox軟件取材日常生活的簡易實驗可操作性強,且制作成本低、制作時間短,并能有效解決角速度與向心加速度難以測量的痛點,因此,本文介紹的3種生活用品均可用于教師課堂演示實驗及學生課外動手實驗,拓展了探究實驗的實施空間.此外,本文借助Origin軟件進行數據擬合,以擬合公式中ω的指數2.011 4為依據呈現向心加速度與角速度平方成正比的關系,避免了只通過數據點的大致趨勢判斷變量間的函數關系,而缺乏嚴謹思維過程的問題.為學生完整而清晰地展現從原始數據到實驗結論的思維過程,體現物理學研究的邏輯性.

