虹與霓現(xiàn)象的MATLAB仿真研究

郭志興 張俊 閆苗苗 黃海強 劉成毅 朱麗娟

(湖北文理學院物理與電子工程學院 湖北 襄陽 441053)

1 引言

霓虹亦稱彩虹，是雨后天晴天空中常見的光學現(xiàn)象.早在3 000多年前的殷商時期，我國甲骨文中就已出現(xiàn)了虹的象形文字.東漢蔡邕的《月令章句》記載了當時對虹形成的外觀條件、虹的方位的認識[1].約公元200年雅典哲學家亞歷山大發(fā)現(xiàn)主彩虹和次級彩虹之間較暗區(qū)域亞歷山大暗帶[2].笛卡爾在1637年指出，彩虹是當太陽光被空氣中的水滴經(jīng)折射—反射—折射形成的[3].1811 年畢奧首次觀測到彩虹射線的內(nèi)入射角非常接近布儒斯特角[4].

20世紀開始霓虹的原理研究從光的折射、反射理論到洛倫茲-米氏散射、德拜散射理論、對水珠形狀影響分析等逐漸深入.文獻[5]從霓虹現(xiàn)象的認識歷史、簡單物理本質(zhì)、幾何原理的推論以及偏振狀態(tài)解釋了霓虹產(chǎn)生的成因.文獻[6]介紹了彩虹產(chǎn)生的物理機理.文獻[7]的作者設計演示了360°的霓虹，并提出在小球背面的反射點處鍍膜以增強霓虹的亮度.文獻[8]推導出了最小偏向角處的入射角.文獻[9]求出了水對紅、紫光的折射率.文獻[10]給出了不同波長光在水中的霓虹視角.文獻[11]簡述了根據(jù)彩虹的特點判斷天氣變化.文獻[12]用幾何畫板軟件再現(xiàn)霓虹的成因.基于前人的研究成果，我們對太陽光經(jīng)過小水珠前后的過程進行深入研究.發(fā)現(xiàn)了在實物實驗中方便測量最小偏向角的方法.

2 成因分析

天空中的小水滴可近似視為小球體.當太陽光以一定的角度照射時，在最小偏向角附近太陽光將以幾乎相同的角度經(jīng)歷多次折射和反射，所以經(jīng)水滴出射的光會集中在最小偏向角附近.當我們從正面觀察從小水滴中射出的光時，可以看到更清晰的彩虹[10].

同時還會受到光照強度、水汽特征等天氣條件.由于水對不同波長光的折射率不同，導致不同顏色光的偏折程度不同，所以我們看到的彩虹是五顏六色的.相對于觀察者，偏向角相同的小水滴一定分布在圓弧上，這就是我們看到的彩虹呈圓弧型的原因.太陽的位置越低，看到的圓弧越完整.所以在夕陽下，我們可以看到近半圓的弧形彩虹；乘坐飛機時，可能看到完整的彩虹[2].

3 光學原理

3.1 虹

虹的光路如圖1.設入射光AB進入小球的入射角i1=∠ABC，折射角i2=∠OBG，自B點射入，經(jīng)兩次折射一次反射從E點射出，則入射光AB與出射光ED夾角即偏向角為

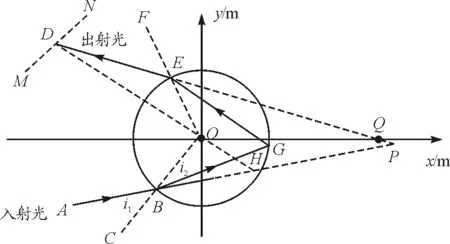
圖1 虹的光路圖

Ds=4i2-2i1

(1)

(2)

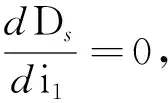
(3)

設入射光與水平線夾角θ，球半徑r，以球心為原點，建立笛卡爾平面坐標系,出射光ED的斜率

kED=tan(θ+Ds)

(4)

輔助線OF的斜率

kOF=tan(arctankED-i1)

(5)

出射光ED與小球交點E坐標(xE,yE)

yE=kOFxE

(6)

因此,光線離開小球時的位置E(xE,yE)和方向kOF就確定了.

3.2 霓

霓的光路如圖2.入射光AB從B點射入，經(jīng)兩次折射兩次反射后從E點射出，偏向角為

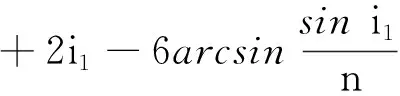
(7)

圖2 霓的光路圖

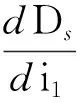
kOF=tan(arctankED+i1)

(8)

xE、yE、xQ的計算方法和虹類似，這里不再重復.

3.3 實物實驗的過程

用PMMA材料、半徑2 cm的小球模擬水滴，吊裝在暗箱內(nèi).接收屏設置在暗箱斜上方，成45°角傾斜放置，可同時顯示虹和霓.用全光譜LED模擬太陽光，光源固定在可旋轉(zhuǎn)角度且有角度刻盤的調(diào)整架上，可精確控制光源的入射角度.實驗裝置內(nèi)部結(jié)構(gòu)圖如圖3所示

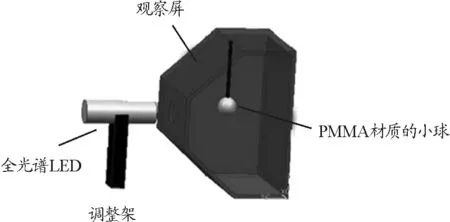
圖3 實驗裝置內(nèi)部結(jié)構(gòu)3D圖

3.4 角度分析

實物實驗中，霓虹的位置與最小偏向角之間的關(guān)系不易測得.我們利用MATLAB推導出兩者之間的關(guān)系.出射光ED的反向延長線與x軸交點Q的坐標(xQ，0)

(9)

所以，從球心向右移動xQ個距離，再旋轉(zhuǎn)arctankED度，與觀察屏的交點D即是霓虹的位置，計算的最小偏向角Ds即θDPA=θ-arctankED.

另一種求最小偏向角的方法：霓虹在觀察屏上的位置D與球心O所在直線DH與入射光AB的夾角θDHA容易測得，而它與偏向角θDPA的差值θPDH容易求得

θPDH=arctankED-arctankDH

(10)

4 基于MATLAB仿真的基本理論知識

4.1 波長到顏色的模型

張卉基于1931CIE標準色度系統(tǒng)和BP神經(jīng)網(wǎng)絡[14]，訓練出RGB到波長的BP網(wǎng)絡模型.表1給出了部分波長光對應的RGB值.

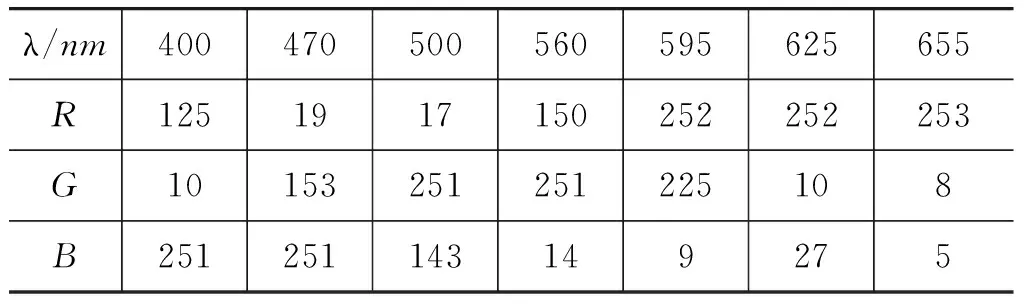
表1 R,G,B三色值與窄帶光中心波長的實驗數(shù)據(jù)

4.2 波長到折射率的模型

根據(jù)ZEMAX軟件玻璃目錄中PMMA所使用的the schott formula公式，PMMA小球的折射率n與波長λ的關(guān)系為

n(λ)2=2.186 4-0.000 244 75λ2+
0.014 155λ-2

(11)

此處波長λ的單位為μm.可見光在PMMA材質(zhì)中的折射率在1.49～1.51之間.將式(11)代入式(2)和式(7)，可分別求出不同顏色光的霓虹視角，如表2所示.

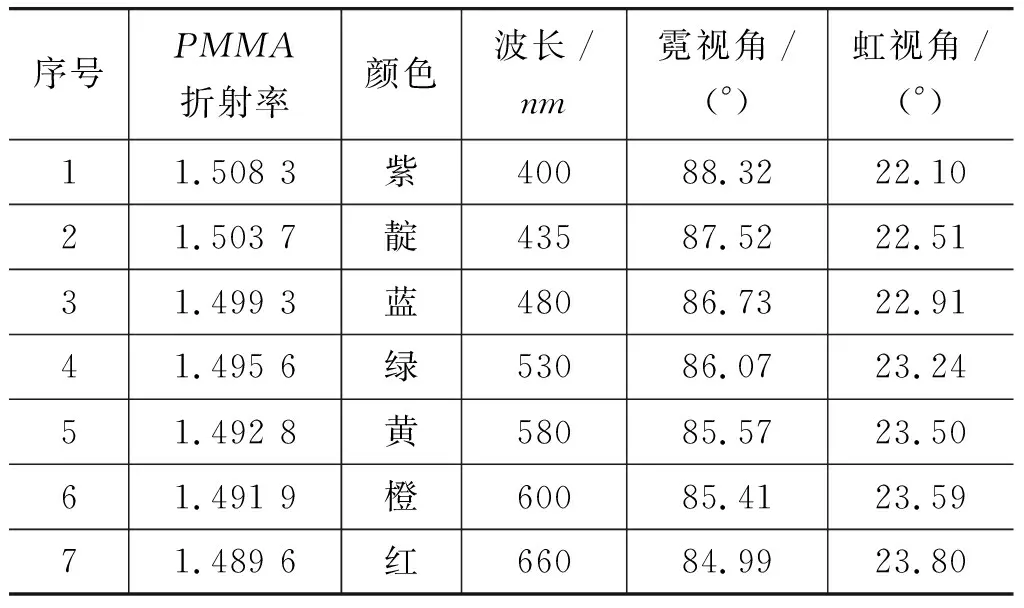
表2 不同波長光在PMMA材質(zhì)中的霓虹視角

對于虹，紅光的視角大于紫光視角，所以虹的紅光在上，紫光在下，最小偏向角約為23.80°.對于霓，紅光的視角小于紫光視角，因此霓內(nèi)紅外紫，最小偏向角約為84.99°.偏向角與入射角的關(guān)系如圖4和圖5所示.

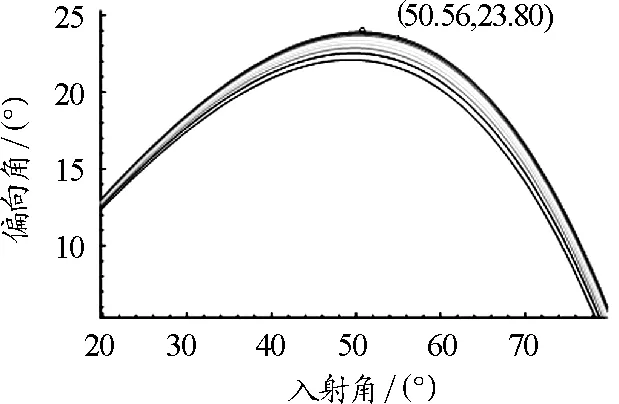
圖4 虹的偏向角與入射角關(guān)系

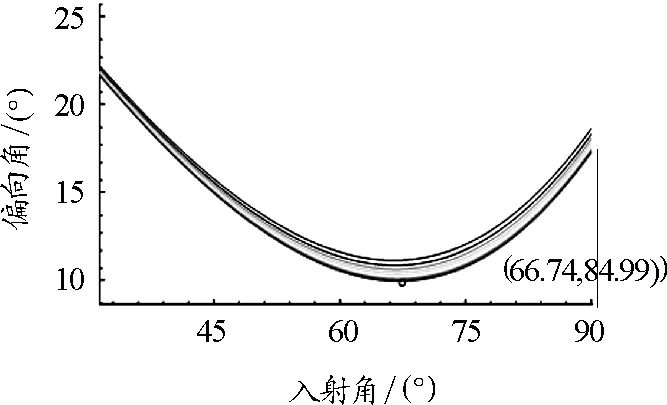
圖5 霓的偏向角與入射角關(guān)系

根據(jù)水對不同波長的可見光的折射率和柯西色散經(jīng)驗公式，水的折射率與波長的關(guān)系可以表示為[13]

n(λ)=1.324+3 076.25λ-2

此處波長λ的單位為nm.

4.3 仿真程序

將小球半徑r、入射光的角度θ，波長λ均以具體數(shù)值表示，根據(jù)折射、反射定律等光學原理繪制仿真圖.程序的主要流程如圖6所示.

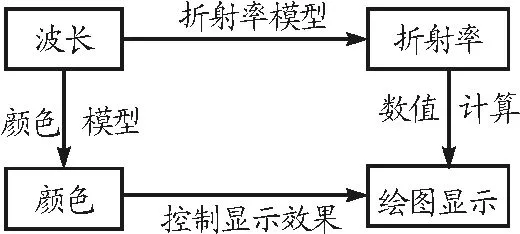
圖6 程序流程圖

radius=2;%小球半徑

k_light=tand(5); %入射光斜率

wave=linspace(0.4,0.7,100);%波長范圍

n1=1.0003;%空氣折射率

n2s=sqrt(2.1864-2.4475e-4.*wave.^2+0.014155./wave.^2); %折射率與波長

theta_i_n=acos(sqrt(((n2/n1)^2-1)/8));%求入射角

theta_reflect_n=asin(n1*sin(theta_i_n)/

n2);%求反射角

5 MATLAB仿真實驗軟件開發(fā)與功能演示

為替代GUI、順應Web潮流，mathworks公司于2016年正式推出MATLAB APP Designer.其界面簡潔，操作簡便，可直接在左側(cè)拖拽出需要的控件，并通過回調(diào)函數(shù)完成各個控件間的參數(shù)傳遞[15].

本文基于MATLAB APP Designer設計仿真軟件，將以上理論轉(zhuǎn)換成程序代碼，通過鍵入虹與霓的主要輸入?yún)?shù)，程序自適應匹配計算，實現(xiàn)虹與霓現(xiàn)象的交互式動態(tài)仿真，仿真實驗結(jié)果證明了該方法的可靠性以及增加仿真實驗環(huán)節(jié)的優(yōu)點.雖然本文設計的仿真APP是針對二維平面的，但只需要對程序代碼和UI界面稍作調(diào)整修改，該仿真APP也可以用在三維立體空間中.

5.1 APP運行結(jié)果

程序代碼經(jīng)過自適應調(diào)整參數(shù)后，可順利運行.在APP的對應窗口中輸入虹與霓的主要參數(shù)，并點擊“虹與霓的MATLAB仿真”按鈕，可在左側(cè)繪圖區(qū)得到計算的圖像，APP右下角是“計算結(jié)果”面板，顯示紫光經(jīng)PMMA小球折射、反射的最小偏向角和入射角等參數(shù).程序運行結(jié)果如圖7所示.

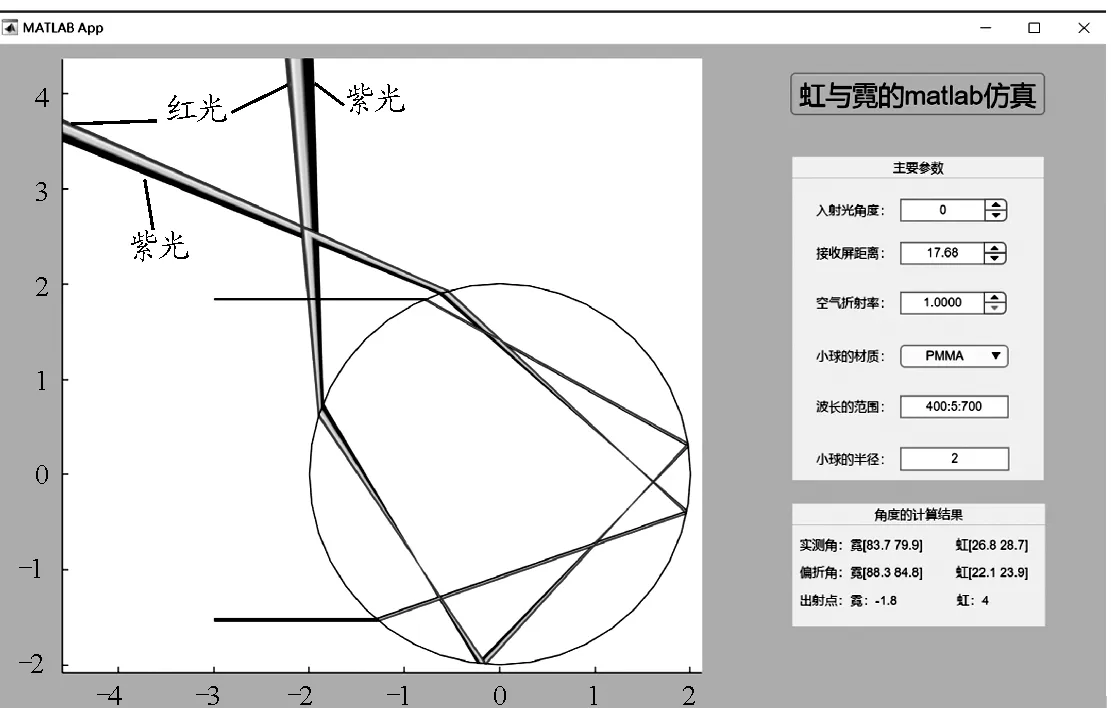
圖7 程序運行結(jié)果

5.2 三維效果展示

將二維圖形經(jīng)過旋轉(zhuǎn)，得到三維立體圖，如圖8所示,上為霓，下為虹,虹所在的圓環(huán)半徑比霓小.

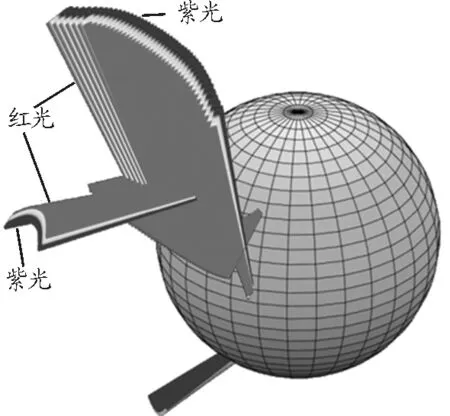
圖8 三維效果圖

6 結(jié)束語

本文基于MATLAB軟件，研究了太陽光經(jīng)過水滴前后的光路，為霓虹的再現(xiàn)提供了一種仿真模擬的方法.并為實驗提供新的理論方法指導，為學生全面掌握虹與霓的光學原理提供支持.