基于條件生成對抗網絡的深度點過程二次預測
卞瑋,李晨龍,侯紅衛
(太原理工大學 數學學院,太原 030000)
0 概述
時序點過程是建模不規則時間間隔事件序列的概率生成模型,并在現實建模中成為處理這一問題的有效數學模型[1]。時序點過程將歷史事件的依賴關系嵌入到強度函數的表達式中,得出事件發生時間間隔的概率密度函數[2],進而進行預測與分析。然而,傳統統計建模方法嚴格限定強度函數形式,從而導致建模能力較弱。近年來,為了解決這一問題,DU等[3]提出將歷史信息嵌入到循環神經網絡(RNN)的隱藏狀態中,利用深度學習的方法拓寬時序點過程的建模途徑。此后,涌現出很多基于RNN 的時序點過程模型[4-5](本文簡稱深度點過程),使得強度函數或者時間間隔概率密度函數更加靈活多變[6-7]。目前,深度點過程在效果上達到甚至超越了傳統點過程模型,為時序點過程在實際中的應用提供了更加有效的方案。然而,深度點過程靈活性的支撐是深度神經網絡參數化的非線性變換,這造成在求解時間預測值時,時間間隔概率密度函數難以顯式表達或者積分不存在解析解的問題,需要通過數值方法近似求解。此外,模型本身的系統誤差也同樣導致時間上的預測值與真實值之間的偏差較大。這兩點原因造成的預測精度不足限制了深度點過程在實際場景中的應用,為深度點過程在實踐中的推廣帶來極大挑戰。
時序點過程序列可以理解為一連串相互關聯的概率分布下的樣本,因此,產生的偏差可以假設為分布上的差異。圖像去運動模糊算法使用條件生成對抗網絡(CGAN)[8]去除因抖動、光暈、運動而產生的圖像模糊,從而提高圖像的清晰度[9-10]。受此思路啟發,本文將深度點過程預測值序列與真實值序列的偏差視為由模型及數值方法帶來的“模糊”,即預測值序列和真實值序列在分布上的差異,使用CGAN 對預測值序列進行二次預測修正。此外,考慮到點過程序列是一個隨機過程而非隨機變量[11],本文采用時序點過程Wasserstein距離的對偶形式及1-Lipschitz 正則項對CGAN 進行約束[12-13],從而提高時間預測的準確度并降低預測的均方誤差。
1 相關工作
1.1 時序點過程
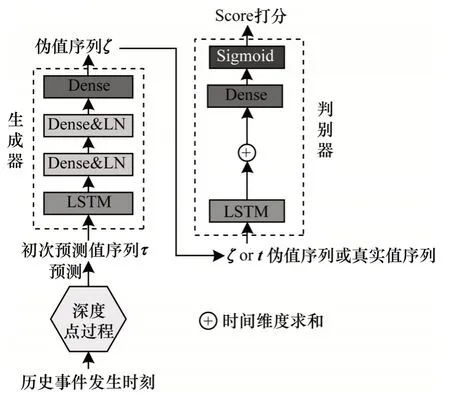
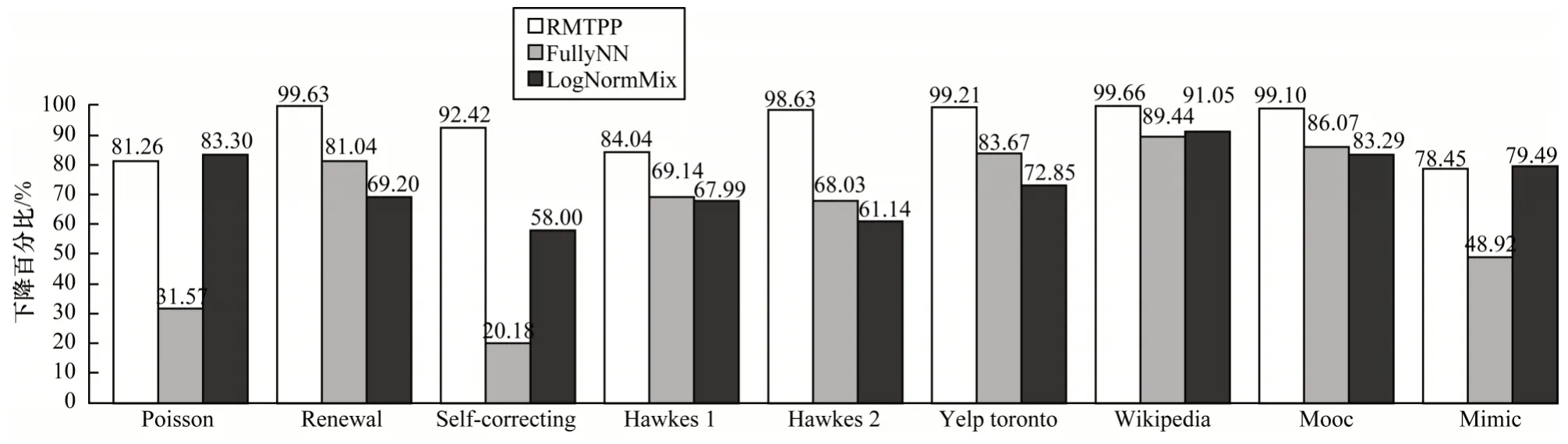
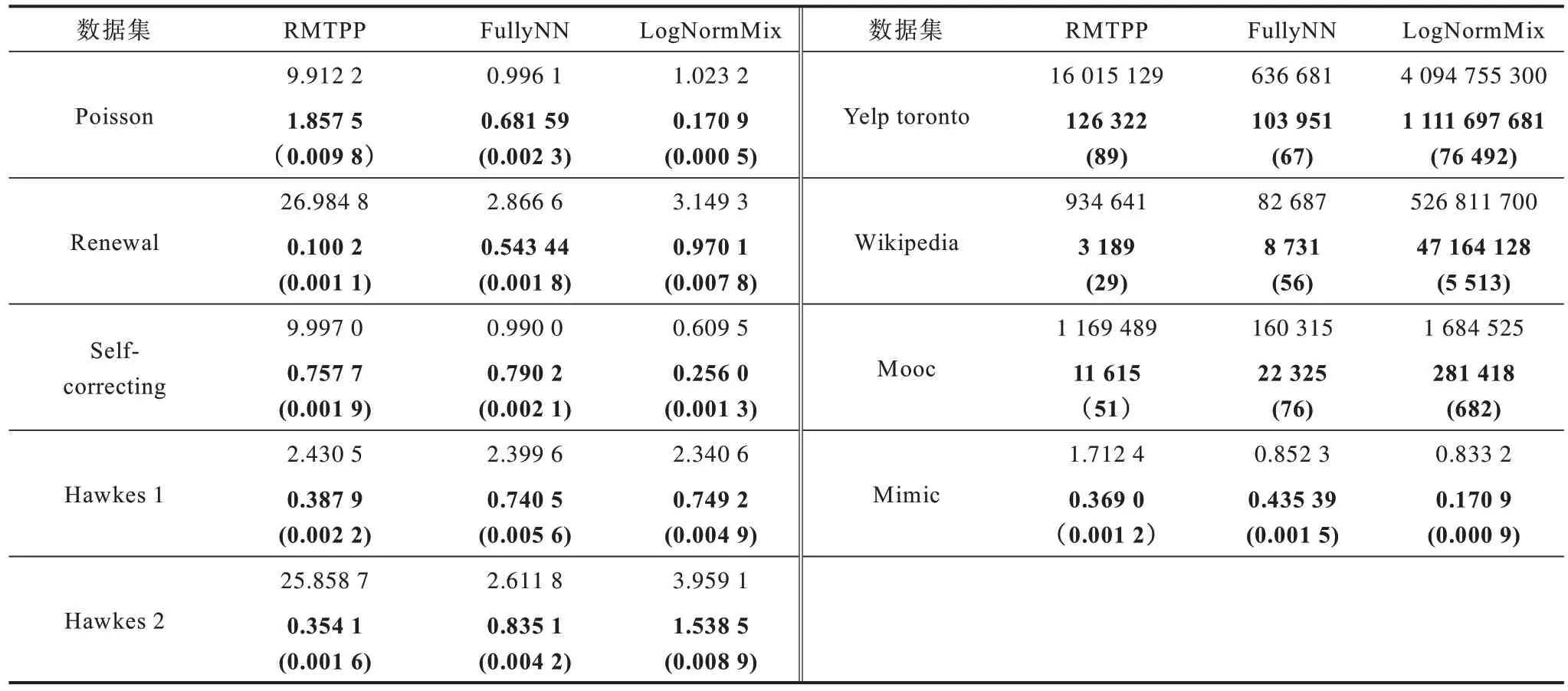
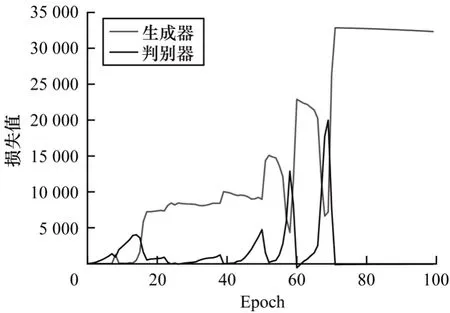
時序點過程是一類特殊的計數過程,如圖1 所示,其對時刻t之前的事件數量進行計數,核心是強度函數λ*(t)。若歷史事件Ht={ti|ti 圖1 時序點過程示意圖Fig.1 Schematic diagram of sequence point process 其中:N(t)表示t時刻之前事件發生的總次數;E(dN(t)|Ht)是給定歷史觀測值Ht的情況下在時間間隔[t,t+dt)中發生的平均事件數。事件發生時間間隔概率密度函數為: 其中:t′為t時刻之前最后一個事件發生的時刻。 深度點過程是以RNN 嵌入式表達歷史事件序列發生的潛在信息,并將強度函數或者事件發生時間間隔概率密度函數視為歷史潛在信息非線性函數的點過程建模方法。相較于傳統統計學上的點過程建模方法,深度點過程利用了神經網絡強大的擬合能力,但同時帶來大量的網絡參數和一系列的非線性變化,對時間預測造成了困難,需要用數值方法來解決。例如,循環標記時序點過程(RMTPP)[3]將條件強度函數形式化為Gompertz 分布: 其中:vt、ht′、wt、bt均由神經網絡得出。進而,事件發生時間間隔概率密度函數為: 由于式(5)中的積分通常不具有解析解,需要使用數值方法近似求解,因此產生了偏差。類似地,全神經網絡時序點過程(FullyNN)[14]通過神經網絡直接輸出強度函數的積分: 但是,強度函數λ*(τ)只能通過Φ(t)求導得出,無法得到顯示表達式,因此,使用中位數t*做預測值。然而,t*需要二分法求方程Φ(t*-t′)=loga2 的根得出,無法獲得解析的最優解,存在數值誤差。同時,由于模型設計上的缺陷,這兩種模型都存在系統誤差,即使巧妙地避開數值誤差也會存在系統誤差。例如,混合對數正態時序點過程(LogNormMix)[15]使用混合對數正態分布擬合時間間隔的概率密度函數: 通過上述過程后不存在數值誤差,但由于大小不可控,容易出現極端值,對預測精度有很大影響,從而導致系統誤差。 SHAHAM等[8]提出的CGAN是一種帶條件約束的概率生成模型。CGAN 引入條件變量y作為輔助信息(類別標簽、其他模態數據等),指導生成器的生成,其損失函數比生成對抗網絡(GAN)[16]多加入額外的條件信息y,如下: 在訓練時,WGAN[17]采用分布間的Wasserstein距離改進GAN,以減緩GAN 訓練不穩定的問題。 圖像去運動模糊的目標是將因抖動、光暈、運動而產生的模糊圖像恢復成清晰圖像[9-10],其模型定義為: 其中:IB、IS和K分別代表向量化的模糊圖像、原始清晰圖像和模糊核;B代表噪聲;?代表卷積運算。圖像去運動模糊過程是式(10)的逆操作,即從模糊圖像IB中還原出清晰圖像IS。由于CGAN 擁有概率生成模型的特性,能夠對圖像分布進行還原變換,因此通常被用來實現上述逆操作。 借鑒圖像去運動模糊的原理,將深度點過程模型由于數值積分與模型本身造成的預測值序列誤差視為與真實值序列分布上的差異[18],然后通過條件生成對抗網絡還原初次預測值序列為真實值序列。 設輸入的初次預測值序列為τ=,對應的真實值序列為t=,二次預測模型假設為: 其中:K為變換矩陣;N=為噪聲序列。 由于原始WGAN 假設處理的數據為隨機變量,這與時序點過程(屬于隨機過程)在樣本空間上存在差異。對此,采用時序點過程之間的Wasserstein 距離來約束生成對抗網絡的訓練以保證理論上的正確性,其具體形式為[13]: 其中:x、y為2 個點過程的實例。 條件生成對抗網絡中生成器的功能是逆向還原初次預測值序列為對應的真實值序列,也稱偽值序列。判別器的目標是最大化生成器還原出偽值序列的時序點過程分布與對應真實值序列的時序點過程分布之間的Wasserstein 距離(初次預測值序列與真實值序列的對應關系為額外的輔助信息): 其中:Pt、Pg分布分別為真實值時序點過程分布、偽值時序點過程分布;φ為Pt、Pg的聯合分布集合;g為CGAN 生成器的函數表示。為了便于計算處理,將式(13)轉化為對偶形式[13]: 其中:f為CGAN 的判別器函數;|·|*為時序點過程之間的距離;‖f‖L≤1 為1-Lipschitz 約束[7]。 首先訓練深度點過程模型得出初次預測值序列,接著對初次預測值序列進行修正[17]。二次預測流程分為3 個步驟: 步驟1將初次預測值序列τ輸入條件生成對抗網絡的生成器g中得出偽值序列g(τ),用ζ=g(τ)。 步驟2將偽值序列ζ及對應的真實值序列t輸入判別器f中分別求出得分f(ζ)、f(t),以判別真假。 步驟3通過對抗訓練得出具備還原能力的生成器。 算法訓練過程中生成器g的損失函數為: 其中:w為生成器g的參數。 判別器d的損失函數為: 其中:V 為判別器d的參數。 二次預測模型中使用的條件生成對抗網絡在結構上采用CGAN+LSTM[19-20]的形式,其中,LSTM(長短期記憶網絡)是RNN 的一種常用變體。本文條件生成對抗網絡結合了CGAN 的概率生成能力和LSTM 的嵌入歷史潛在信息的能力,以達到準確還原初次預測值序列點過程分布并得到修正后二次預測值序列的目的[21]。在網絡結構上,按作用可分為歷史潛在信息讀取、空間變換以及生成器/判別器輸出層3個模塊,如圖2所示。 圖2 條件生成對抗網絡結構Fig.2 CGAN structure 2.3.1 歷史潛在信息讀取 在生成器和判別器中都需要將輸入的序列(生成器為初次預測值序列,判別器為偽值序列或者真實值序列)中包含的歷史潛在信息嵌入到神經網絡中[22]。在生成器和判別器中,先使用LSTM 逐時間步讀取序列中的數據,提取歷史潛在信息。在保證分布轉換前后時間連續的前提下,得到固定特征維度為d(d>1)的向量表示: 其中:x∈Rl×1為生成器或判別器的輸入;v0∈Rl×d為對應的歷史潛在信息向量;LSTM 表示LSTM 網絡。 2.3.2 空間變換 在生成器中,通過LSTM 取得歷史潛在信息向量后,需要使網絡具備調整讀取到的歷史潛在信息為真實歷史潛在信息的能力[23],網絡中借助全連接層的空間變換和整合信息的能力來實現這一目的。 首先,將v0通過一個全連接層,變換潛在歷史信息向量的空間維度d→h(h>d),從而到達更高的維度空間: 其中:Dense1表示全連接層;v1∈Rl×h。 變換空間之后,為了整合高維度空間帶來的信息,使用2 個連續降低特征維度的全連接層h→k(k 其中:Dense2、Dense3表示2 個全連接層;v2∈Rl×k;v3∈Rl×n。 2.3.3 生成器和判別器的輸出層 生成器的功能是得到一組序列長度與輸入序列相同并且值大于零的時間序列,因此,在結構上首先采用一個全連接層將調整后的歷史潛在信息整合為維度是l×1 的向量,然后經過Sigmoid 函數將向量值的范圍約束為大于零,最后輸出一組與輸入序列同時間步長的偽值序列。以上過程形式上可以表示為: 其中:vg∈Rl×n表示生成器經過LSTM 及信息空間變換后的向量;vg∈Rl×n;?∈Rl×1;Dense4表示全連接層;Sigmoid 表示Sigmoid 函數。 判別器的功能是輸出序列真假評分,評分越高說明輸入序列為真的可能性越大。在網絡結構上,首先將偽值序列或者真實值序列的歷史潛在信息向量在時間步維度上相加,然后經過一個全連接層整合信息,最后通過Sigmoid 函數輸出大于零的評分。以上過程形式上可以表示為: 其中:vd∈Rl×n表示判別器經過LSTM 及信息空間變換后的向量;v5∈R1×n;v6∈R1×n;Score ∈R1×1;Dense5表示全連接層。如圖2 所示,除最后一層外,結合層歸一化操作(LN)[25]與Dense 層來緩解過擬合問題并加速訓練。 為了檢驗二次預測方法的有效性,本文分別選取5 個仿真數據集和4 個真實數據集進行實驗,數據均以Python 字典形式儲存在.pickle 文件中。4 種用于仿真實驗的數據參數設置如下: 1)齊次泊松過程(Poisson)。齊次泊松過程的條件強度函數形式為λ*(t)=1。 2)更新過程(Renewal)。更新過程的時間間隔服從對數正態概率密度函數: 參數設置為μ=1.0,σ=6.0。 3)自校正過程(Self-correcting)。自校正過程的條件強度函數形式為: 4)霍克斯過程(Hawkes)。霍克斯過程的條件強度函數形式為: 對于霍克斯過程,分別設置兩組參數: (1)M=1,μ=0.02,α1=0.8,β1=1。 (2)M=2,μ=0.02,α1=0.4,β1=1,α2=0.4,β2=20。 真實數據集采用飯館評論數據集Yelp toronto、網絡慕課交互數據集Mooc、重癥監護醫學數據集Mimic 和維基百科修改數據集Wikipedia。真實數據集描述如下: 1)Yelp toronto 數據集來自對多倫多300 家最受歡迎的餐廳的評論序列,每條記錄都表示某個餐廳的顧客光顧的時間序列。 2)Wikipedia 公共數據集是在維基百科編輯情況序列,其選擇一個月內編輯次數最多的1 000 個頁面作為研究對象,生成157 474 條用戶交互數據。 3)Mooc 數據集是哈佛大學和麻省理工學院聯合發布的公開數據集,包含7 047 名學生在Mooc 在線課程中的97 類互動信息。 4)Mimic 數據集是由貝斯以色列迪康醫學中心(BIDMC)提供的重癥監護醫療信息公開數據集,其記錄了4 萬多名患者的75 類診斷治療數據,并選取至少出現3 次的病人作為研究對象。 本文選取3 種被學術界認可的深度點過程模型,分別為循環標記時序點過程(RMTPP)、全神經網絡時序點過程(FullyNN)、混合對數正態時序點過程(LogNormMix),以產生初步的預測數據。其中,MTPP、FullyNN 用于探究數值誤差和系統誤差同時存在時的偏差,LogNormMix 用于探究由于系統誤差而產生的偏差。此外,選取均方誤差(RMSE)作為實驗的度量指標,并對比二次預測前后的差異來驗證本文方法的有效性。 模型采用Adam 優化方法動態調整學習率,避免模型參數陷入次優解。優化方法的初始學習率設置為α=1e-4,一階和二階指數衰減率分別設置為β1=0.5,β2=0.9。模型的訓練批量設置為64,訓練100 次循環并應用提前停止的方法,在每次循環訓練過程中,訓練5/10 次判別器后訓練1 次生成器。 為了從客觀上反映模型的二次修正效果,本文對比RMTPP、FullyNN、LogNormMix 在經過模型二次預測前后時間預測RMSE 值以及其下降的百分比,實驗結果如圖3、表1 所示,在表1 中,加粗表示二次預測及標準差。 圖3 二次預測后RMSE 下降百分比Fig.3 Reduction percentage of RMSE after the second prediction 表1 二次預測前后的RMSE值Table 1 RMSE values before and after the second prediction 從圖3 可以看出,二次預測后RMSE 均有不同程度的降低,其中最大降低99.86%,最小降低21.18%,平均降低77.02%,這說明本文所提模型擁有優異的修正能力,同時印證了理論假設的合理性。從RMTPP、FullyNN、LogNormMix 之間的差異上看,平均下降百分比由高到低排序為RMTPP(92.48%)>LogNormMix(74.03%)>FullyNN(64.32%),這可解釋為:RMTPP 采用單峰Gompertz 分布擬合強度函數,系統誤差高,且求期望數值積分時反常積分不收斂,數值誤差較大;LogNormMix 采用混合對數正態分布計算期望時受到預測方差極端值的影響而造成預測值波動較大;FullyNN 輸出條件強度函數的積分且預測求解中位數時采用類似二分法的方法求根,誤差較小。因此,3 個模型誤差大小排序為RMTPP >LogNormMix >FullyNN,更大的誤差使得偽樣本與真實樣本更易區分,判別器在對抗訓練中更易達到最優解從而促進生成器的學習。 為檢驗模型訓練抵抗隨機因素影響的魯棒性,對每個數據的每種基線方法都進行10 次訓練,得出均值和標準差如表1 所示,從中可以看出,標準差的均值在0.1%以內,這表明模型訓練穩定,受隨機擾動影響較小,魯棒性較強。 本文所提模型對FullyNN 在Hawkes 1 數據集上訓練時的損失函數如圖4 所示,因為其他損失函數收斂情況大同小異,所以不再冗余表述。從圖4 可以看出,判別器的損失在最開始的迭代中逐次提高,這時判別器的判別能力逐漸提升導致生成器損失降低。當判別器損失達到第一個峰值后,生成器損失逐漸提高,開始具備一定的生成能力,之后當生成器生成能力提高到第一個峰值后判別器損失又逐步提高。模型在對抗訓練約70 個迭代周期后,生成器損失維持動態穩定同時判別器損失接近0,達到均衡狀態[26]。較少的迭代次數也表明生成器的能力容易在對抗訓練中得到有效提高。 圖4 損失函數曲線Fig.4 Loss function curves 本文建立一種深度點過程二次預測模型。使用條件生成對抗網絡對深度點過程的預測數據進行二次預測,通過逆變換初次預測值序列為真實時序值序列在點過程上的差異,以降低因模型系統誤差和數值計算誤差而帶來的預測偏差。在條件生成對抗網絡的損失函數中利用時序點過程Wasserstein 距離的對偶形式及其1-Lipschitz 約束來訓練網絡。實驗結果表明,本文模型可以穩定有效地降低時間預測偏差,同時條件生成對抗網絡的損失容易達到對抗平衡。下一步考慮將其他類型的生成對抗網絡及自注意力網絡應用于深度點過程二次預測模型中,以提高時間預測效果。

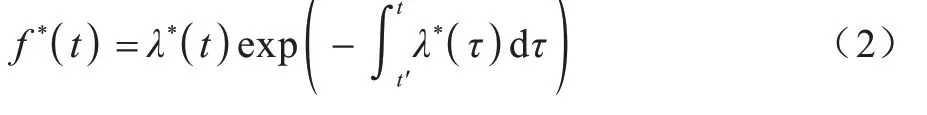
1.2 深度點過程及預測瓶頸
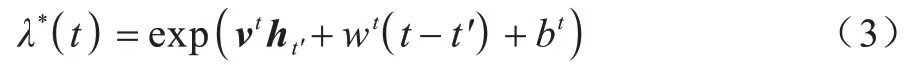
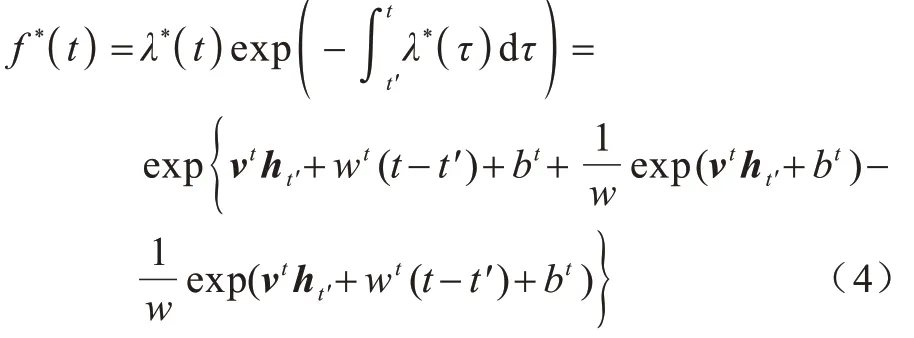



1.3 條件生成對抗網絡
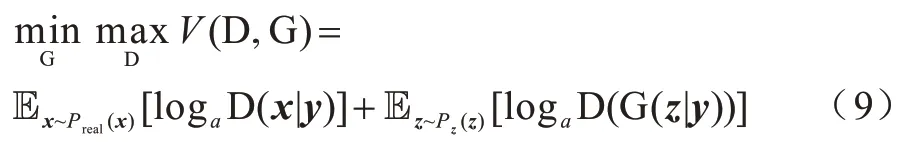
1.4 圖像去運動模糊

2 深度點過程二次預測模型
2.1 二次預測原理
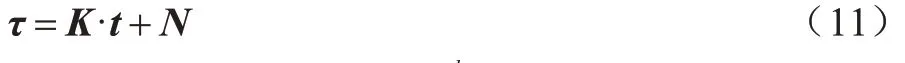

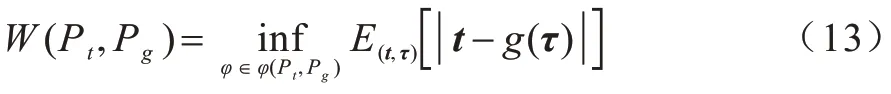
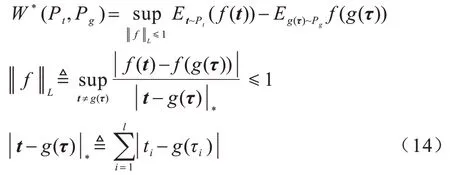
2.2 二次預測算法及訓練流程

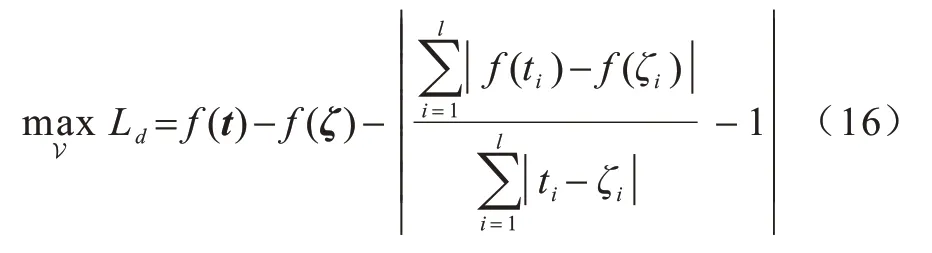
2.3 條件生成對抗網絡結構





3 實驗結果與分析
3.1 數據集
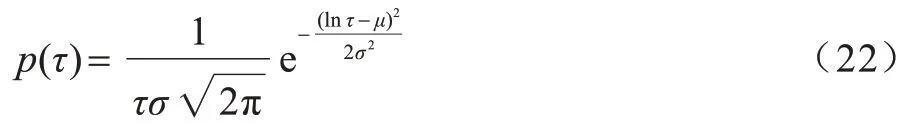

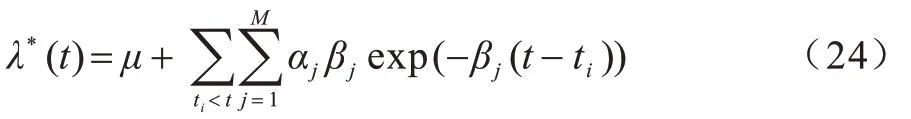
3.2 數據基準模型和實驗設置
3.3 結果分析
3.4 模型損失
4 結束語

