巖溶區(qū)橋梁基樁水平承載特性及影響因素分析
劉逸飛, 王琛
(湖南湘江新區(qū)投資集團(tuán)有限公司, 湖南 長(zhǎng)沙 410000)
橋梁基樁除承受上部結(jié)構(gòu)和車(chē)輛載重傳遞下來(lái)的豎向荷載外,還會(huì)受到車(chē)輛行駛產(chǎn)生的離心力、風(fēng)荷載等水平向荷載及偏心彎矩,若忽視水平荷載和偏心彎矩對(duì)基樁產(chǎn)生的不利影響,會(huì)給橋梁基樁帶來(lái)極大安全隱患,嚴(yán)重時(shí)可能導(dǎo)致事故。為深入分析橋梁基樁的水平承載特性及受力變形機(jī)理,趙明華等通過(guò)室內(nèi)模型試驗(yàn),研究了復(fù)雜荷載作用下橋梁雙樁基礎(chǔ)的內(nèi)力與位移變化發(fā)展規(guī)律及破壞模式;張浩等基于實(shí)際工程,分析了路基邊載作用下軟土地基橋梁樁柱的位移特征和受力機(jī)制;Sawant V. A.等通過(guò)有限元數(shù)值計(jì)算,分析了水平荷載作用下樁身彎矩和位移分布規(guī)律;趙海鵬等基于高性能有限單元法,分析了多層地基水平受荷樁的受力變形特性,反映了非線性樁-土相互作用;胡文韜等基于線彈性地基反力法,提出了水平荷載作用下階梯形變截面樁內(nèi)力及變形解析算法;邢康宇等基于雙曲線水平荷載傳遞模型,考慮樁-土體系變形的非線性特征,分析了成層土中軸橫受荷樁的水平響應(yīng)。總體來(lái)說(shuō),橫向受荷基樁的受力和變形計(jì)算方法主要包括有限桿單元法、冪級(jí)數(shù)法、有限差分法和傳遞矩陣法等,其中傳遞矩陣法計(jì)算過(guò)程清楚,可考慮樁身尺寸變化、樁周土體各向異性及復(fù)雜邊界條件等,便于實(shí)際工程應(yīng)用。本文以位于巖溶區(qū)的某橋梁基樁為依托,分析基樁的水平受荷特性,建立相應(yīng)撓曲微分方程,并基于傳遞矩陣法推導(dǎo)基樁樁身內(nèi)力與位移的理論解答,編制相應(yīng)計(jì)算程序,對(duì)橋梁基樁的受力與變形影響因素進(jìn)行分析。
1 樁身內(nèi)力與位移計(jì)算的理論解答
實(shí)際工程中,由于橋梁基樁的截面尺寸、樁身強(qiáng)度及樁周土體性質(zhì)等不盡相同,樁身受力變形特性存在較大差異。為考慮樁身參數(shù)和樁周土體的各向異性,建立圖1所示基樁簡(jiǎn)化計(jì)算模型。樁頂受軸向荷載P0、橫向荷載Q0及彎矩M0的作用,基樁長(zhǎng)度為L(zhǎng),其中地面或局部沖刷線以上的自由段長(zhǎng)度為l0,位于地面以下的入土段深度為lp。依次將樁
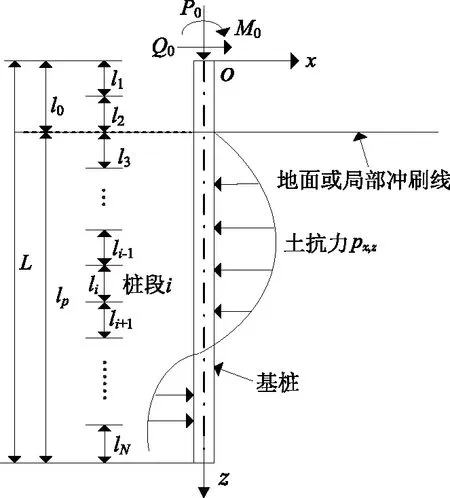
圖1 基樁簡(jiǎn)化計(jì)算模型
身劃分為N段,每段長(zhǎng)度為L(zhǎng)/N。
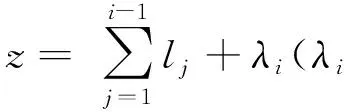
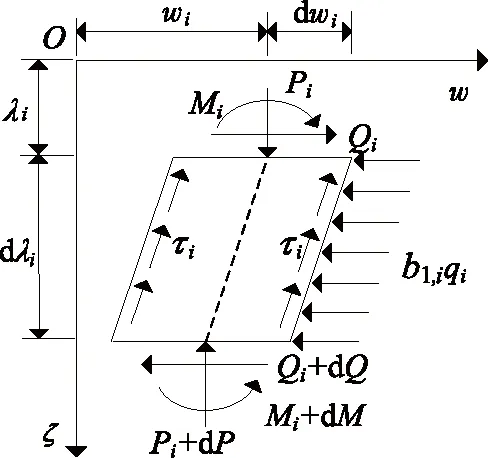
圖2 基樁第i微元段受力分析示意圖
基于Winkler彈性地基理論及m法的基本假定,對(duì)于入土段基樁,根據(jù)圖2取第i微元段進(jìn)行受力分析,建立該樁段的撓曲微分方程:
b1,iqi=0
(1)
式中:EiIi為第i微元段樁身抗彎剛度;wi為水平位移;λi為計(jì)算點(diǎn)到該樁段頂點(diǎn)的距離;P0,i為第i微元段樁頂軸力;fi為樁身軸力增長(zhǎng)系數(shù);b1,i為基樁有效計(jì)算寬度;qi為第i微元段對(duì)應(yīng)巖土層的水平地基抗力,按式(2)計(jì)算。
(2)
式中:m為地基水平抗力比例系數(shù)。
可根據(jù)《公路橋涵地基與基礎(chǔ)設(shè)計(jì)規(guī)范》查表確定m,i≤2時(shí),m=0;也可開(kāi)展現(xiàn)場(chǎng)試驗(yàn)測(cè)得相應(yīng)參數(shù),根據(jù)《建筑樁基技術(shù)規(guī)范》由實(shí)測(cè)參數(shù)按式(3)確定m。
(3)
式中:Hcr為基樁水平臨界荷載;xcr為臨界水平位移;vx為樁頂水平位移系數(shù)。
將式(2)代入式(1),整理得:
(4)
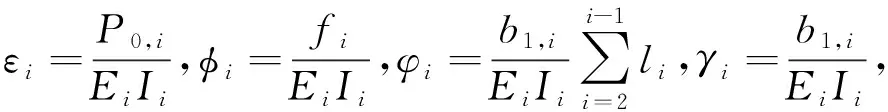
γiλi)=0
(5)
根據(jù)冪級(jí)數(shù)法對(duì)式(5)求解,設(shè)其解答為:
(6)
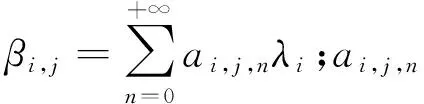
基于Euler-Bernoulli理論,第i微元段的樁身轉(zhuǎn)角θi、彎矩Mi和剪力Qi可表示為:
(7)
采用比較系數(shù)法消除待定系數(shù)ηi,j,得:
(8)
式中:wi,0、θi,0、Mi,0、Qi,0分別為樁段λi=0處的水平位移、轉(zhuǎn)角、彎矩和剪力;XXi為樁段i的內(nèi)力與位移傳遞矩陣,可表示為:
XXi=Xi(Xi|λi=0)-1
(9)
(10)
(11)
另外,各樁段之間滿足內(nèi)力與位移的傳遞協(xié)調(diào)條件,即第i與i-1兩相鄰樁段狀態(tài)變量相等。將所有樁段的基樁傳遞矩陣連乘,即可建立第i段與第1段之間內(nèi)力與位移的傳遞關(guān)系:
(12)
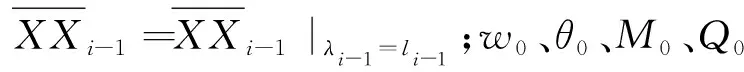
綜上,結(jié)合基樁受荷情況和樁頂、樁底邊界條件,即可求解基樁內(nèi)力與位移,其求解過(guò)程可通過(guò)編制MATLAB程序進(jìn)行。
2 工程概況及影響因素分析
2.1 工程概況
湖南長(zhǎng)沙湘府路(河西段)快速化改造工程中某鉆孔灌注樁,樁長(zhǎng)L=19.5 m,其中自由段長(zhǎng)2.0 m,入土段長(zhǎng)17.5 m,樁徑D=1.8 m,樁身為C30混凝土和直徑28 mm的HRB400鋼筋通長(zhǎng)配置。樁側(cè)土層自上而下依次為雜填土、粉質(zhì)黏土、強(qiáng)風(fēng)化白云巖及強(qiáng)風(fēng)化灰質(zhì)白云巖,局部揭露巖層存在溶洞,不具備嵌巖樁設(shè)計(jì)的地質(zhì)條件。各土層參數(shù)見(jiàn)表1。

表1 巖土層分布及力學(xué)參數(shù)
2.2 理論與數(shù)值計(jì)算對(duì)比驗(yàn)證
當(dāng)樁頂受荷情況為水平荷載Q0=80 kN、豎向荷載P0=50 kN時(shí),通過(guò)理論和數(shù)值計(jì)算(數(shù)值計(jì)算模型見(jiàn)圖3),得到圖4、圖5所示樁身水平位移和彎矩隨深度的變化。
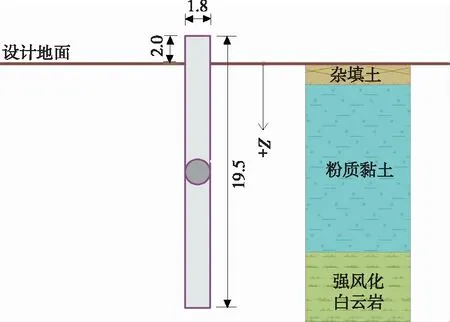
圖3 數(shù)值計(jì)算模型示意圖(單位:m)
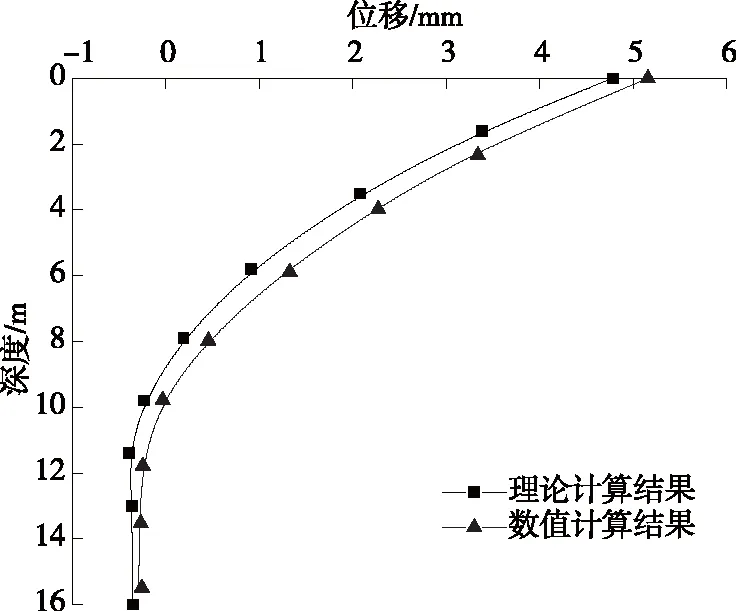
圖4 樁身水平位移計(jì)算結(jié)果對(duì)比

圖5 樁身彎矩計(jì)算結(jié)果對(duì)比
由圖4、圖5可知:理論和數(shù)值計(jì)算的樁身水平位移及彎矩變化趨勢(shì)較吻合,驗(yàn)證了理論解答的合理性;數(shù)值計(jì)算結(jié)果略大于理論計(jì)算結(jié)果,這是因?yàn)閿?shù)值計(jì)算對(duì)地基水平抗力比例系數(shù)進(jìn)行了一定程度折減,導(dǎo)致基樁內(nèi)力計(jì)算結(jié)果偏大。
2.3 影響因素分析
為研究水平荷載Q0、樁身抗彎剛度EI及地基水平抗力比例系數(shù)m對(duì)樁頂自由、樁端固定的橋梁基樁水平承載性能的影響,在保持其他參數(shù)不變的情況下,對(duì)水平荷載Q0=100 kN、200 kN、300 kN,樁身剛度EI=300 MN·m2、500 MN·m2、700 MN·m2,地基水平抗力比例系數(shù)m=6 MN/m4、9 MN/m4、12 MN/m4時(shí)基樁彎矩和位移進(jìn)行對(duì)比分析。
2.3.1 樁頂水平荷載的影響
假定樁身剛度和樁側(cè)土體抗力比例系數(shù)等參數(shù)不變,通過(guò)傳遞矩陣法分別計(jì)算水平荷載Q0為100 kN、200 kN和300 kN時(shí)樁身水平位移和彎矩,結(jié)果見(jiàn)圖6、圖7。
從圖6、圖7可以看出:樁身水平位移隨樁頂水平荷載增加而增大,樁身彎矩隨埋深向下呈現(xiàn)先增大后減小的趨勢(shì),且樁身彎矩隨樁頂水平荷載增加而顯著增大。樁頂水平荷載為100 kN、200 kN、300 kN時(shí),樁頂水平位移分別為12.7 mm、23.6 mm、34.6 mm,樁身最大彎矩分別為315 kN·m、500 kN·m、690 kN·m,后者與前者相比,樁頂水平荷載每增加100 kN,對(duì)應(yīng)地面處水平位移分別增加85.8%、46.6%,樁身最大彎矩分別增加58.7%、38.0%。不同水平荷載作用下,樁身最大彎矩出現(xiàn)在基樁埋深3~4 m位置,即約2倍樁徑處。可見(jiàn),樁頂水平荷載對(duì)基樁受力變形有較大影響,且水平荷載越大其影響程度越大,相對(duì)而言樁身位移對(duì)水平荷載變化的敏感程度更大。

圖6 不同水平荷載Q0下樁身水平位移
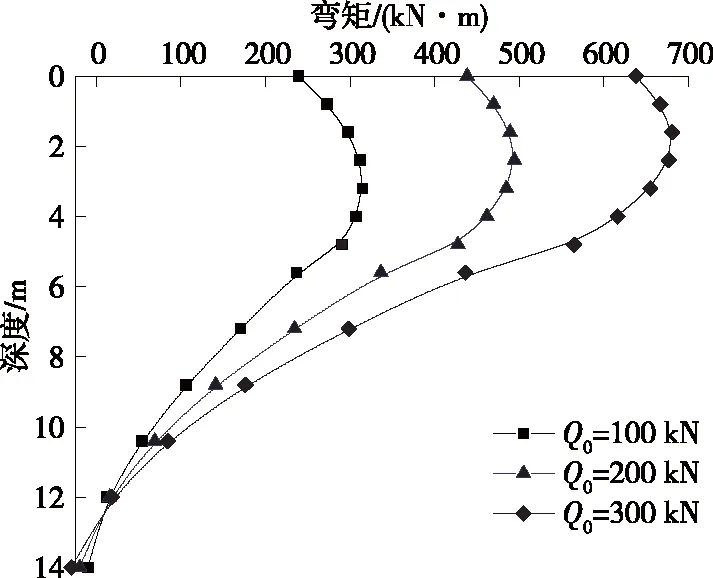
圖7 不同水平荷載Q0下樁身彎矩
2.3.2 樁身抗彎剛度的影響
為研究樁身抗彎剛度EI對(duì)橋梁基樁水平承載特性的影響,以樁頂水平荷載為100 kN、地基水平抗力比例系數(shù)為6 MN/m4為例,計(jì)算EI分別為300 MN·m2、500 MN·m2、700 MN·m2時(shí)樁身水平位移和彎矩,結(jié)果見(jiàn)圖8、圖9。
從圖8、圖9可以看出:樁身抗彎剛度為300 MN·m2、500 MN·m2、700 MN·m2時(shí),樁頂水平位移分別為17.2 mm、15.0 mm、12.7 mm,樁身最大彎矩分別為314.7 kN·m、331.8 kN·m、348.8 kN·m。隨樁身抗彎剛度增加,樁身彎矩小幅增加,樁身水平位移稍有減小。表明盲目通過(guò)增大樁身抗彎剛度來(lái)提高基樁水平承載能力并不能達(dá)到較好的效果,反而會(huì)增加工程成本。這與文獻(xiàn)[16]的結(jié)論一致。
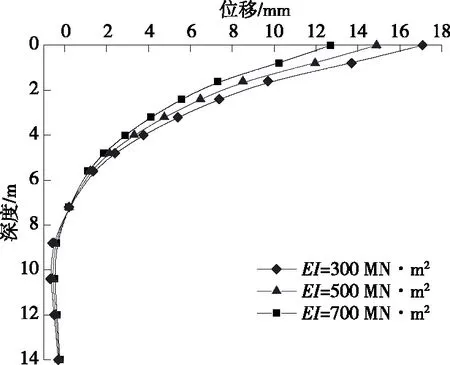
圖8 不同樁身抗彎剛度EI下樁身水平位移
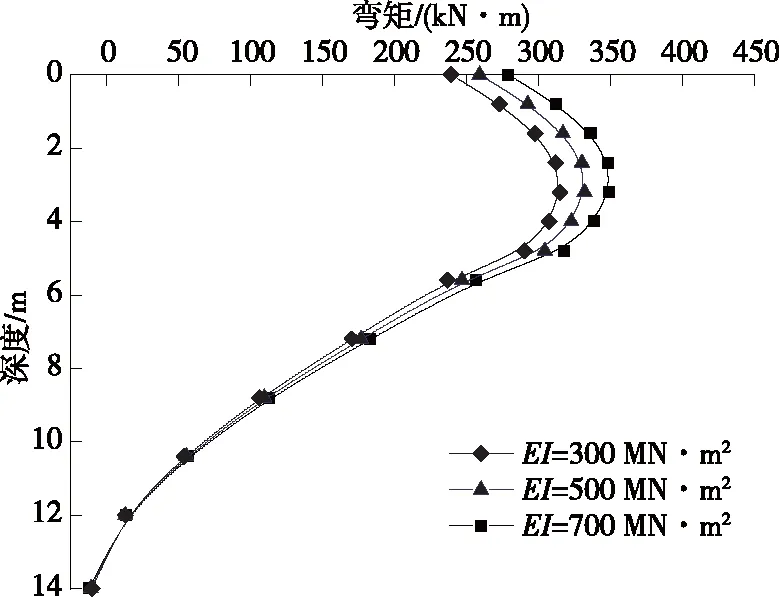
圖9 不同樁身抗彎剛度EI下樁身彎矩
2.3.3 地基水平抗力比例系數(shù)的影響
以樁頂水平荷載為200 kN、樁身剛度為300 MN·m2為例,計(jì)算不同地基水平抗力比例系數(shù)m下樁身水平位移和彎矩,結(jié)果見(jiàn)圖10、圖11。
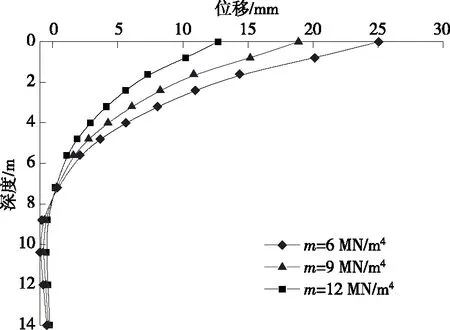
圖10 不同地基水平抗力比例系數(shù)m下樁身水平位移
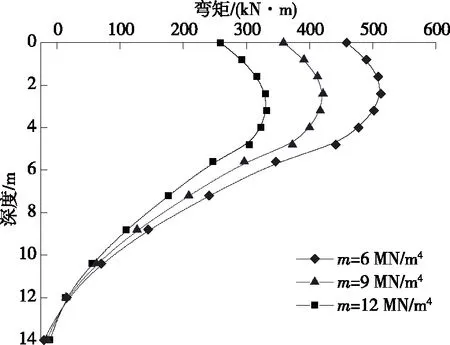
圖11 不同地基水平抗力比例系數(shù)m下樁身彎矩
由圖10、圖11可知:地基土體水平抗力比例系數(shù)m為6 MN/m4、9 MN/m4、12 MN/m4時(shí),樁頂水平位移分別為25.1 mm、18.8 mm、12.7 mm,樁身最大彎矩分別為512.6 kN·m、421.3 kN·m、338.7 kN·m。地基土體水平抗力比例系數(shù)對(duì)樁身水平位移和彎矩的影響較大,這是因?yàn)閙值越大,土體越密實(shí),硬度越高,能提供的土抗力越大,在相同水平荷載作用下樁身水平位移和彎矩值越小。在其他條件不變的情況下,提高樁側(cè)地基土體強(qiáng)度,增大地基土體水平抗力系數(shù)可有效減小基樁內(nèi)力和位移,提高基樁水平承載能力。
3 結(jié)論
本文根據(jù)橋梁基樁的水平承載特性,建立樁-土相互作用簡(jiǎn)化計(jì)算模型及樁身?yè)锨⒎址匠蹋趥鬟f矩陣法推導(dǎo)基樁內(nèi)力與位移的理論解答,分析水平荷載、樁身抗彎剛度及地基水平抗力比例系數(shù)對(duì)基樁內(nèi)力與位移的影響,得到以下主要結(jié)論:
(1) 樁身水平位移和彎矩均隨樁頂水平荷載增加而顯著增大,樁身彎矩隨埋深向下呈現(xiàn)先增大后減小的趨勢(shì),樁身最大彎矩出現(xiàn)在基樁埋深2倍樁徑處。
(2) 隨樁身抗彎剛度增加樁身彎矩小幅增加,樁身水平位移稍有減小,表明增大樁身抗彎剛度不能明顯提高基樁水平承載能力。
(3) 樁身水平位移和彎矩隨地基土體水平抗力比例系數(shù)增加而減小,增大地基土體水平抗力系數(shù)可在一定程度上提高基樁水平承載能力。

