可變速發電電動機電壓波形的優化

胡金明， 茍智德， 王建剛， 孫玉田， 陶大軍， 張春莉， 李桂芬， 胡 剛， 賀儒飛

(1.哈動國家水力發電設備工程技術研究中心有限公司，哈爾濱 150040；2.哈爾濱電機廠有限責任公司，哈爾濱 150040；3.大型電機電氣與傳熱技術國家地方聯合工程研究中心 (哈爾濱理工大學)，哈爾濱 150080；4.南方電網調峰調頻發電有限公司，廣州 510950)

0 前言

隨著能源消費結構調整的深入和電氣化的推進，未來30年，以風電、光伏發電為首的可再生能源將持續快速發展，成為增速最快的能源。在快速轉型情景下，預計到達2050年，可再生能源的占比將增長至45%。但是，受到地理位置、氣候條件等環境因素的影響，風電、光伏發電等可再生能源的發電功率具有較強的間歇性與不確定性，導致電能質量降低、調頻調峰難度增大等問題，影響電網運行的穩定性[1-2]。為了抑制間歇式電源出力的波動性，保證電網的可靠運行，需要在電力系統中增加儲能電源。抽水蓄能電站由于其良好的調節性和運行的靈活性，得以大規模發展，在儲能中占據領先地位[3-5]。常規抽水蓄能電站采用同步發電機，轉速不可調節，使水泵水輪機無法運行在最佳運行區，嚴重影響水泵水輪機的運行性能和效率[6-8]。可變速抽水蓄能機組相較于常規抽蓄機組的主要優勢在于:首先，具備自動跟蹤電網頻率變化的能力，在水泵工況下，通過平滑調速實現輸入功率連續可調，為系統提供了相應的頻率自動控制容量；其次，通過改變交流勵磁系統輸出電壓的頻率實現轉速和有功功率調節，使機組在水輪機工況也能工作在最佳運行區域，提高了運行效率和有功功率調節性能；另外，可變速抽水蓄能機組適應水頭和輸出功率的變化范圍更廣、穩定運行區域更寬，并且通過定子繞組短路利用交流勵磁裝置即可實現零速自起動。因此，發展可變速抽水蓄能機組，對于提高電網安全穩定運行水平以及提升新能源資源利用率等，具有重要意義[9-11]。

可變速發電電動機轉子繞組與變流器連接，定子側與電網連接。變流器利用直流母線電壓通過逆變產生三相交流方波電壓通入電機轉子繞組[12-13]。變流器常用的調制方法有正弦脈寬調制技術、帶三次諧波注入的正弦脈寬調制技術、空間矢量調制技術，其中空間矢量調制技術由于其具有數字化程度高、母線電壓利用率高的特點備受青睞[14-15]。

電機在正常運行中，定子繞組感應電動勢中的諧波會產生諧波電流，進而在電機繞組中產生諧波電動勢，引起電勢波形的畸變，導致電機本身附加損耗成倍增加，電機繞組溫度升高，且會導致電機振動噪聲，效率下降，壽命降低，故空載電壓波形畸變率可作為考察發電機性能的重要特性[16-19]。本文通過分析其諧波產生的原因提出改進措施，采用斜槽和開輔助槽等方法可以很好的削弱諧波影響，以降低波形畸變，提高電壓波形質量，起到降低損耗和溫升，提升電機效率的目的[20-24]。

1 空載性能分析

1.1 有限元建模

由于樣機定子繞組每極每相槽數為整數，其主要參數見表1，為了便于分析，取一個磁極區域(一半單元電機)作為有限元求解模型。模型的定子外圓gh和轉子內圓ab為一類齊次邊界條件，ac和bd、eg和fh為半周期邊界條件，如圖1所示。其瞬態磁場采用矢量磁位描述，假設位移電流及定子鐵芯中的渦流忽略不計，定、轉子繞組端部漏抗通過電路方程和電磁場方程耦合計入，則電機內二維瞬態電磁場方程的邊值形式可由式(1)表示。

圖1 求解場域

表1 樣機主要參數

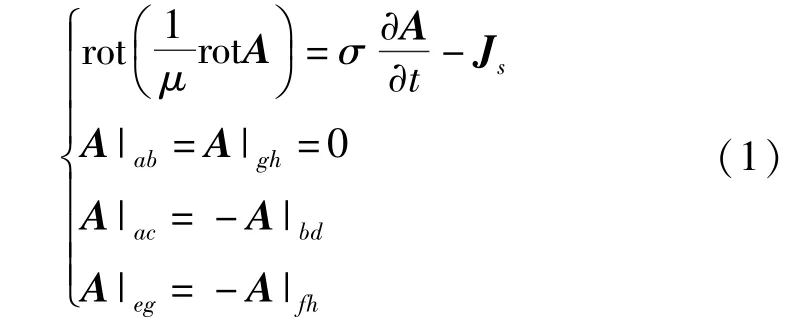
1.2 空載工況有限元仿真

依據90kW樣機的結構特點采用瞬態磁場有限元法對其空載磁場進行了分析，為準確獲得有限元計算結果，需適當加密網格剖分，如圖2所示。轉子繞組通入三相正弦交流勵磁電流，瞬態場求解后其磁場分布如圖3所示，磁密分布如圖4所示，三相線電壓波形如圖5所示。

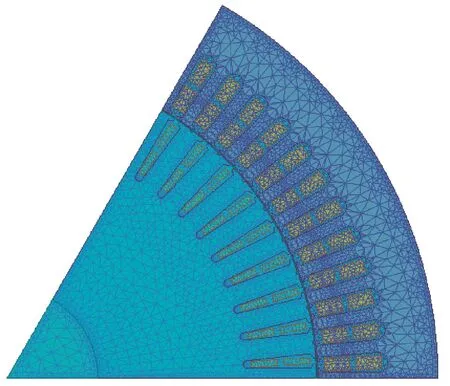
圖2 有限元網格剖分

圖3 空載磁場分布

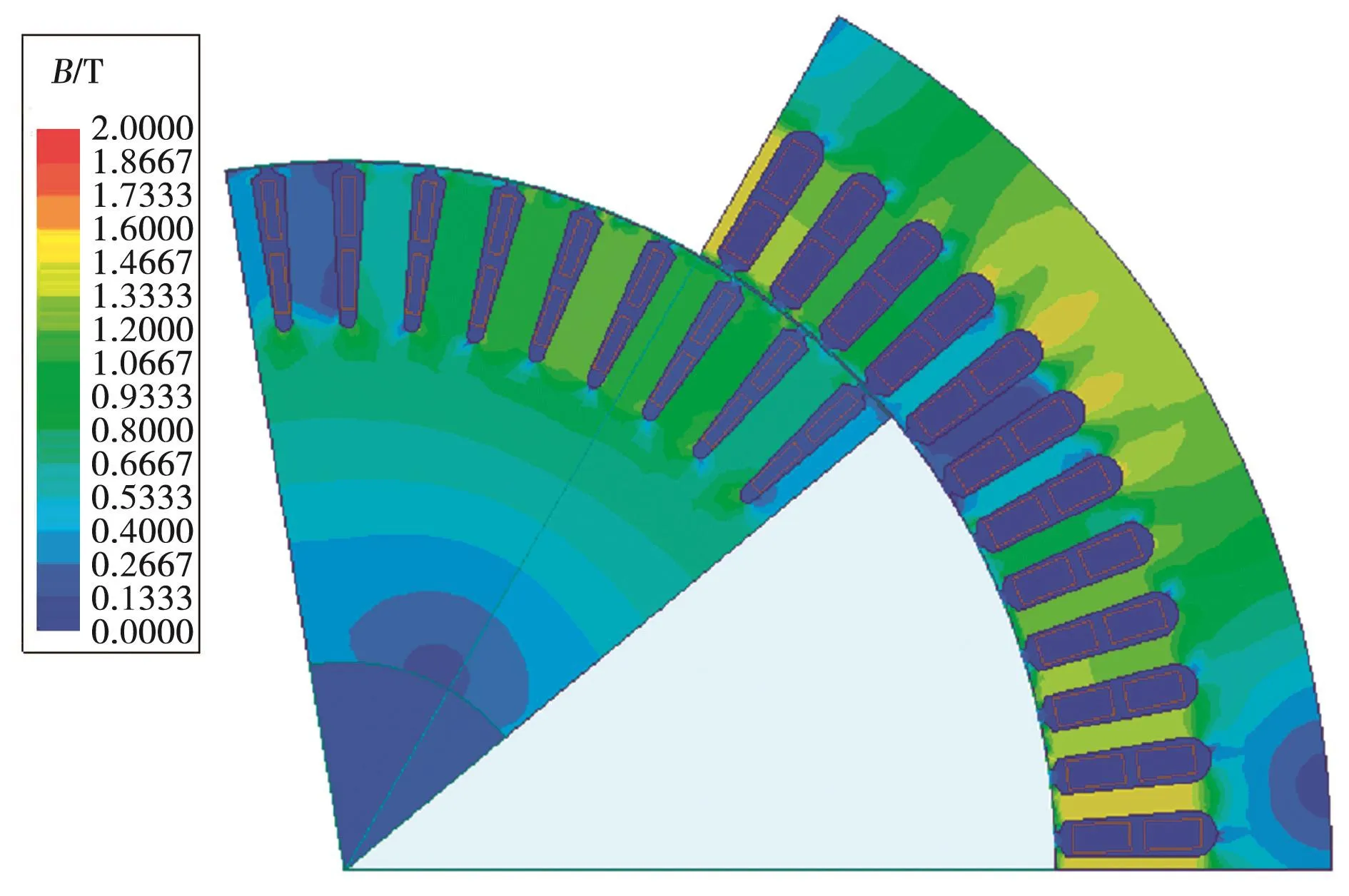
圖4 空載磁密分布

由圖5可見，本臺樣機的電壓波形質量較差，波形畸變嚴重，取空載電壓一個周期波形，對其進行傅里葉分解，諧波分布如圖6所示(為分析諧波情況，圖中未繪制基波)。根據文獻[14]計算得到空載線電壓波形畸變率為7.58%，超出國家標準 《旋轉發電機定額和性能》(GB 755)規定。

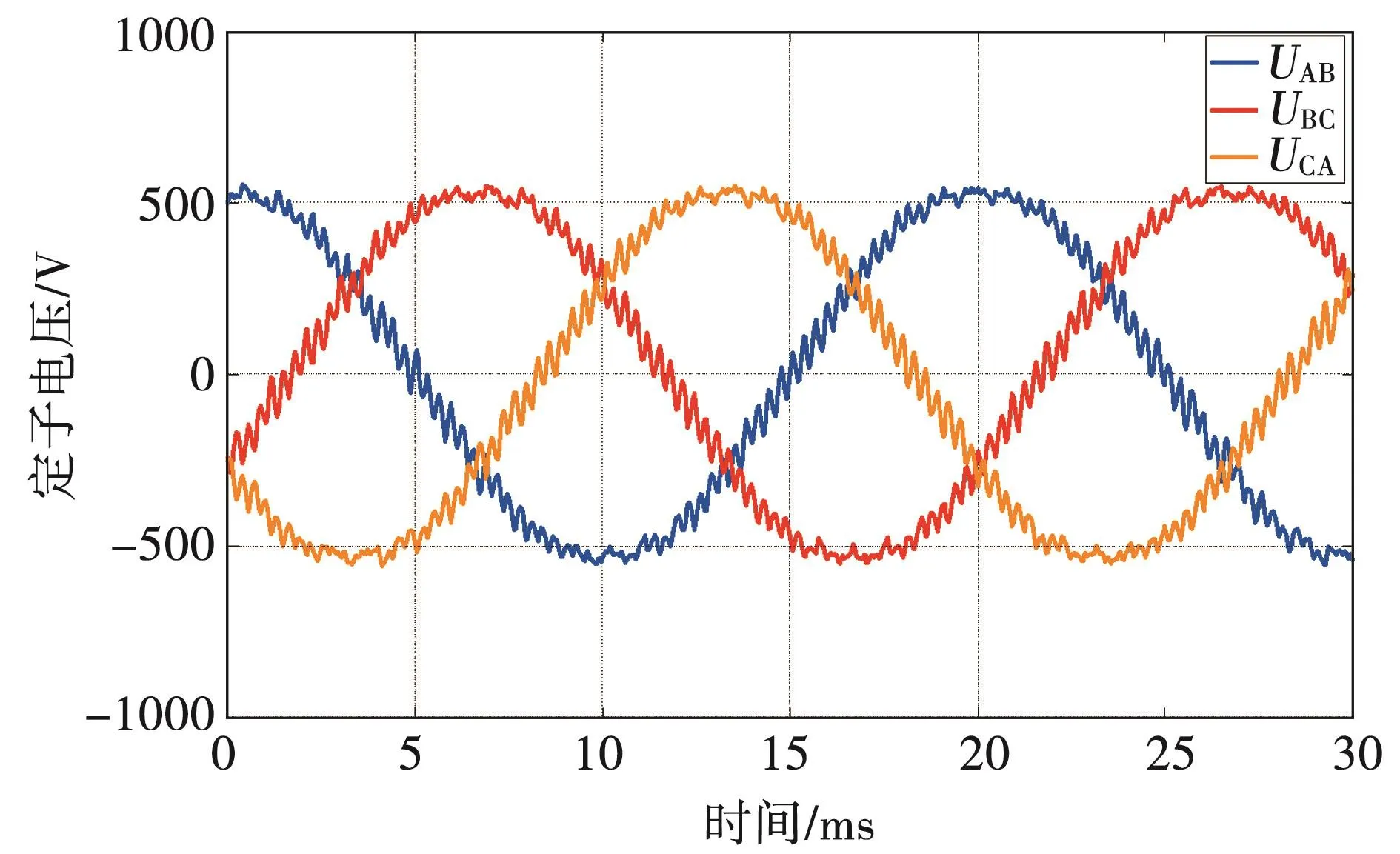
圖5 三相線電壓波形

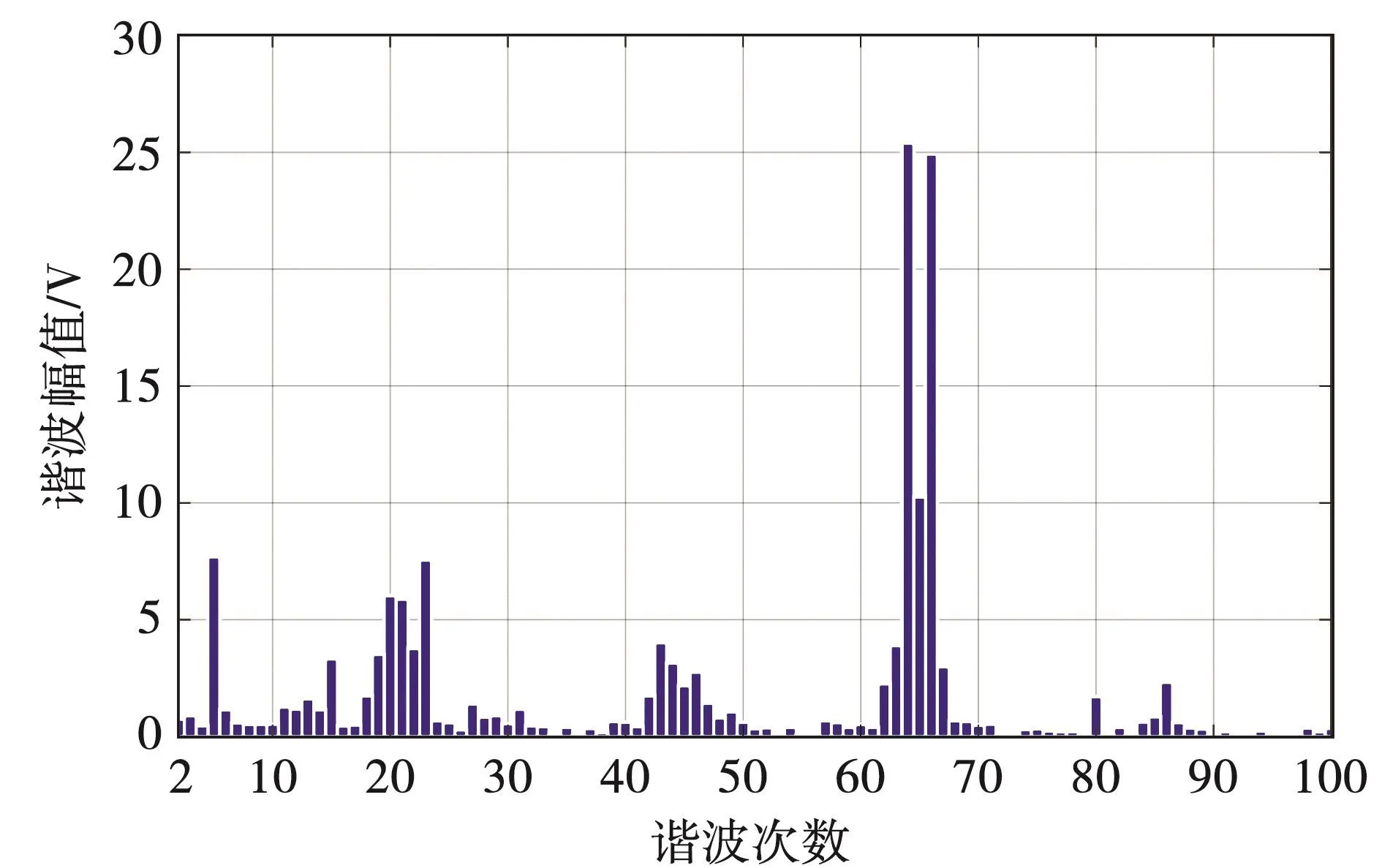
圖6 諧波分布

2 諧波來源分析

2.1 變流器諧波對電壓波形的影響

可變速發電電動機轉子繞組連接變流器，變流器輸出電壓為由常用的空間矢量調制方法(SVM)調制得到的方波電壓，含有多頻次諧波。本文提取轉子電壓中的諧波，將其作為有限元分析的邊界條件，對比分析轉子諧波下定子側波形畸變。

當可變速發電電動機并網空載運行時，定子繞組電流為0，其狀態方程:輸入向量為u＝[udruqr]T，狀態向量為 x＝[idriqr]T，輸出向量為 y＝[udsuqs]T，方程如式(2)所示，使用此狀態方程可搭建空載電機模型。

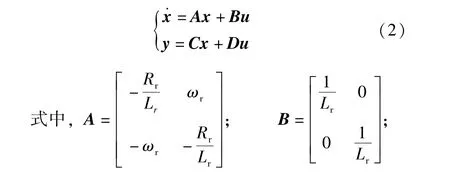
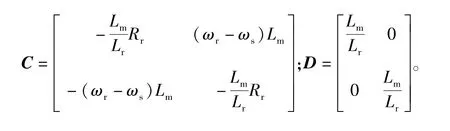
此時電磁轉矩為0。

利用SVM調制技術建立如圖7所示的開環控制下空載工況仿真模型。

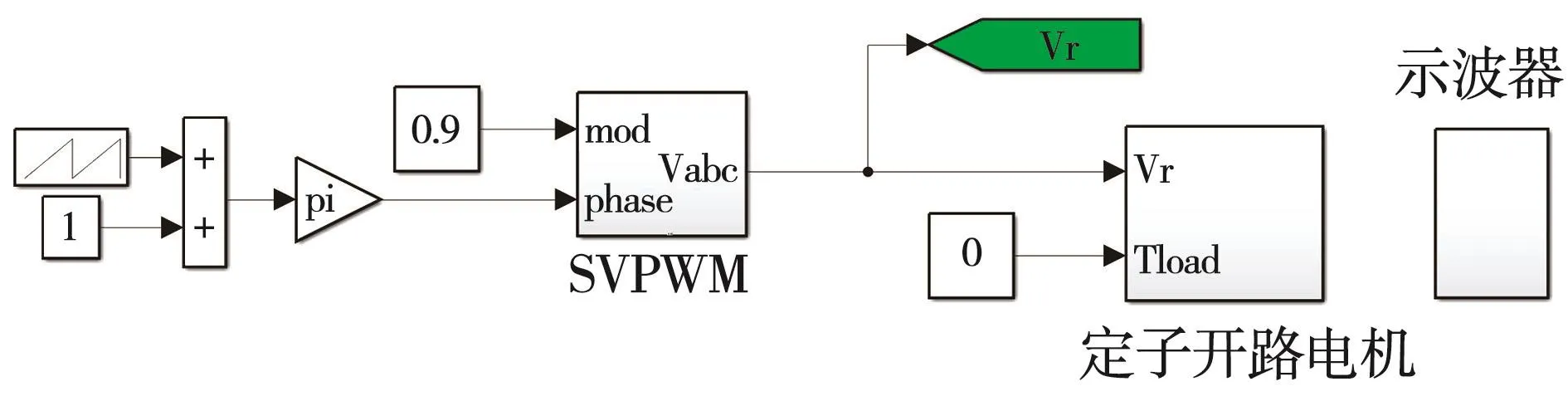
圖7 基于SVM的可變速電機空載仿真模型

仿真得到SVM調制的轉子電壓如圖8所示，定子電壓如圖9所示，對轉子電壓進行傅里葉分解得到諧波分布如圖10所示，包含多頻次諧波。

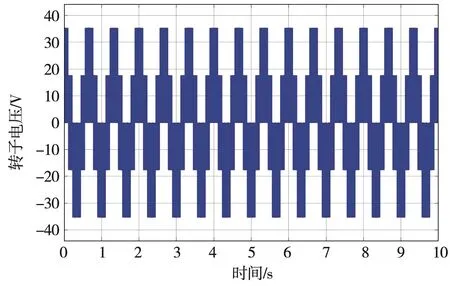
圖8 SVM調制的轉子電壓

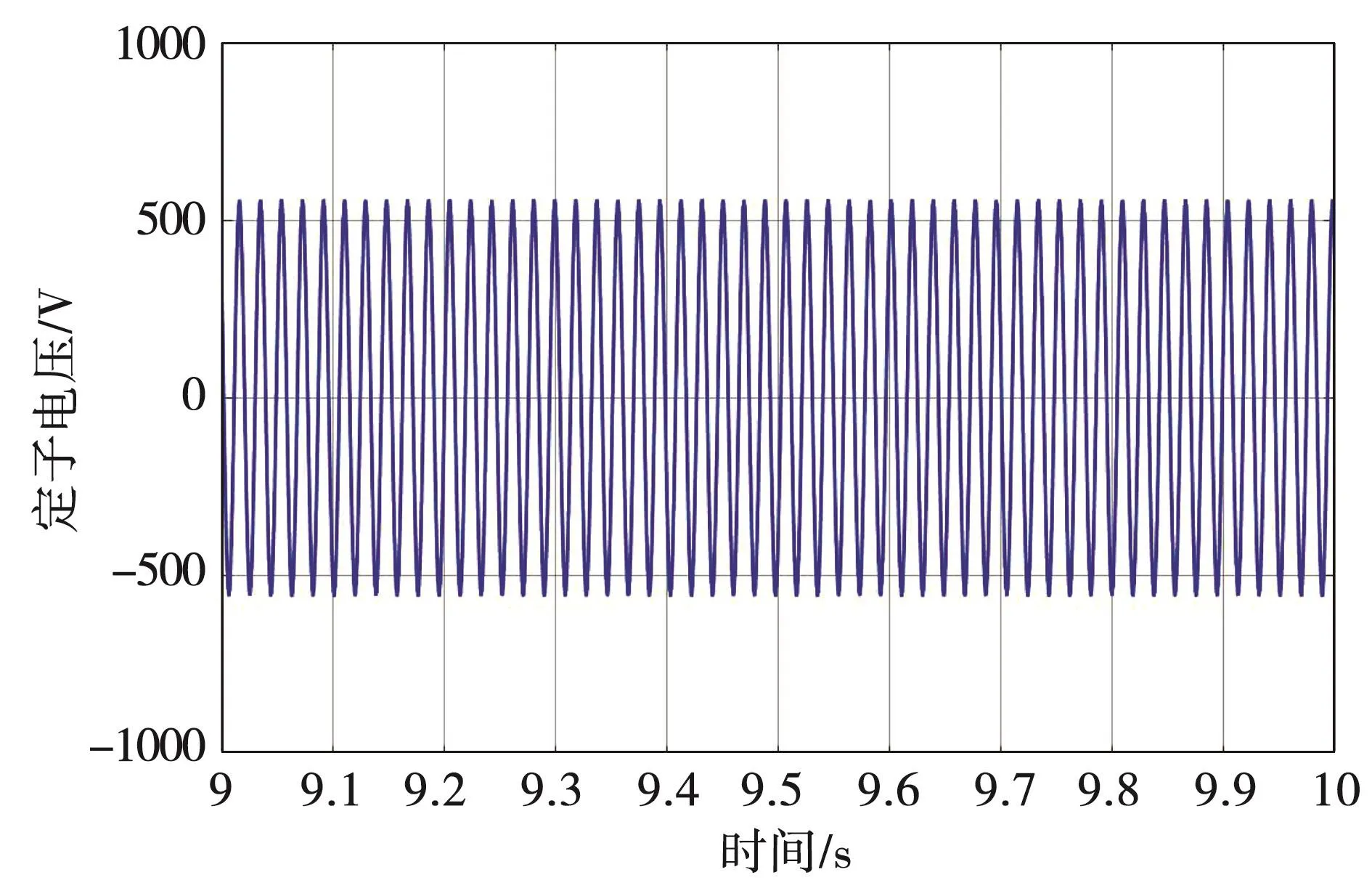
圖9 定子電壓

圖10 轉子電壓諧波分布

提取變流器的諧波分布作為有限元仿真的勵磁電流邊界，如下式:

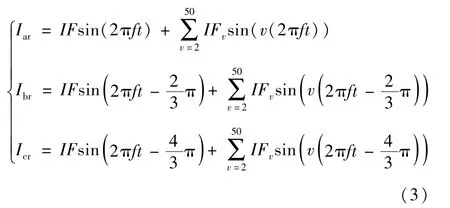
式中，Iar、Ibr、Icr分別為轉子三相勵磁電流；IF為基波勵磁電流幅值；IFv為v次諧波勵磁電流幅值。

仿真得到考慮變流器諧波和不考慮變流器諧波情況下定子電壓的對比如圖11所示，觀察圖11可以看出，考慮變流器諧波后，定子電壓的波形變化不大。對考慮變流器諧波的定子電壓波形進行傅里葉分解后諧波分布如圖12所示，波形畸變率為7.94%，相比不考慮變流器諧波時有所增大，故變流器諧波對電壓波形有些影響，需要在電機設計時予以考慮。

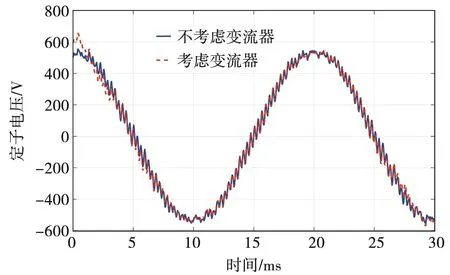
圖11 定子電壓對比

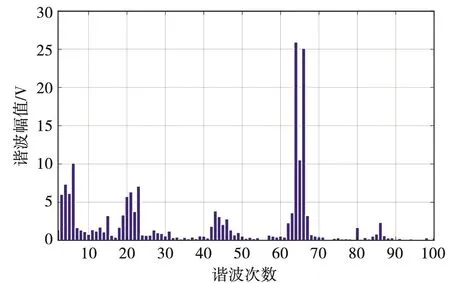
圖12 諧波分布

2.2 電機本體齒諧波對電壓波形的影響

由于電機鐵芯齒槽部分的磁導率不同，氣隙磁通密度的分布波形會受到影響，齒下氣隙較小磁導大，反之槽口氣隙大磁導小，影響繞組里的感應電動勢波形，造成波形中出現較強的高次諧波，即齒諧波。

仔細觀察圖6和圖12諧波分布圖可以發現，在次同步速900r/min時高次諧波中64次和66次諧波幅值較大，即為此電機的齒諧波。為找出其齒諧波的分布規律，本文仿真不同轉差率下定子電壓齒諧波的分布情況，見表2。

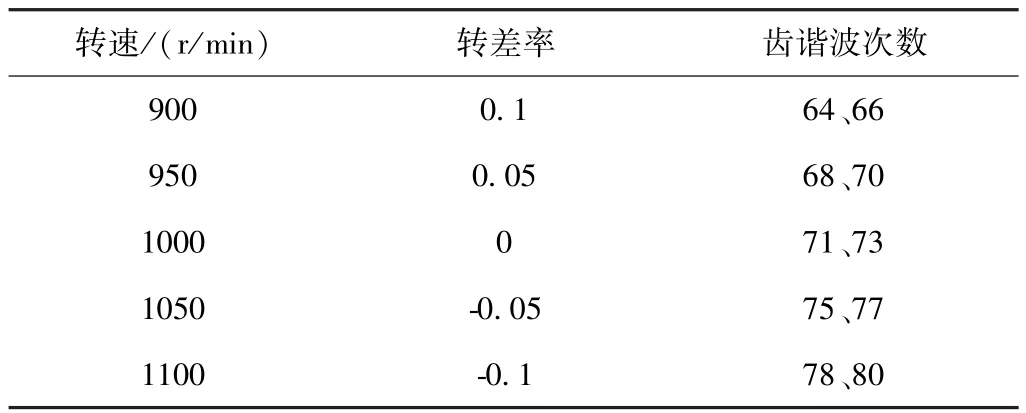
表2 齒諧波頻次

通過表2可以得出可變速發電電動機的齒諧波滿足如下公式，為可變速發電電動機的特有齒諧波性質。

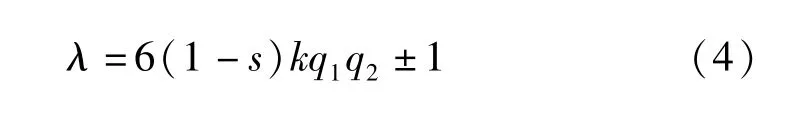
式中，λ為齒諧波次數；s為轉差率；k為常數1、2、3…；q1、q2分別為定、轉子每極每相槽數。

3 樣機試驗與優化

3.1 樣機試驗

樣機試驗平臺由拖動機、可變速發電電動機樣機、變流器組成，實物如圖13所示。

圖13 樣機試驗平臺

對可變速發電電動機進行了空載特性試驗，試驗過程為:保持在額定轉速下，調節勵磁電流從1A增加至21A，記錄定子線電壓有效值。試驗值與有限元仿真值對比結果見表3，繪制曲線如圖14所示。

圖14 空載特性曲線對比

表3 空載特性對比值

對比空載特性曲線的仿真值和試驗值可以看出，其結果差異很小，可以證明有限元仿真結果的正確性。試驗并網前后定子繞組的開路電壓如圖15所示。由圖可知，并網前定子線電壓波形畸變率較高。

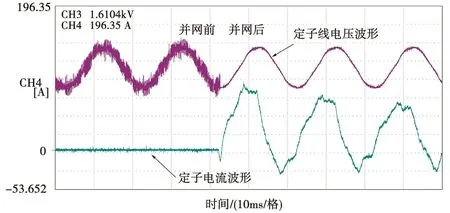
圖15 并網瞬間定子電壓、電流波形

3.2 電壓波形質量的優化

齒諧波不能通過采用分布式繞組或繞組短節距的方法加以消除或者削弱。齒諧波是由于齒槽部分的磁導不同造成的，如果采用半閉口槽、磁性槽楔、或者無鐵芯結構，則可以削弱甚至不會產生齒諧波，另外通過增加每極每相槽數、斜槽、分數槽等均可以大幅度削弱電勢齒諧波。本文綜合考慮后，決定采用斜槽和在定子齒上開輔助槽 (輔助槽局部放大如圖16所示)的方法來削弱齒諧波的影響。

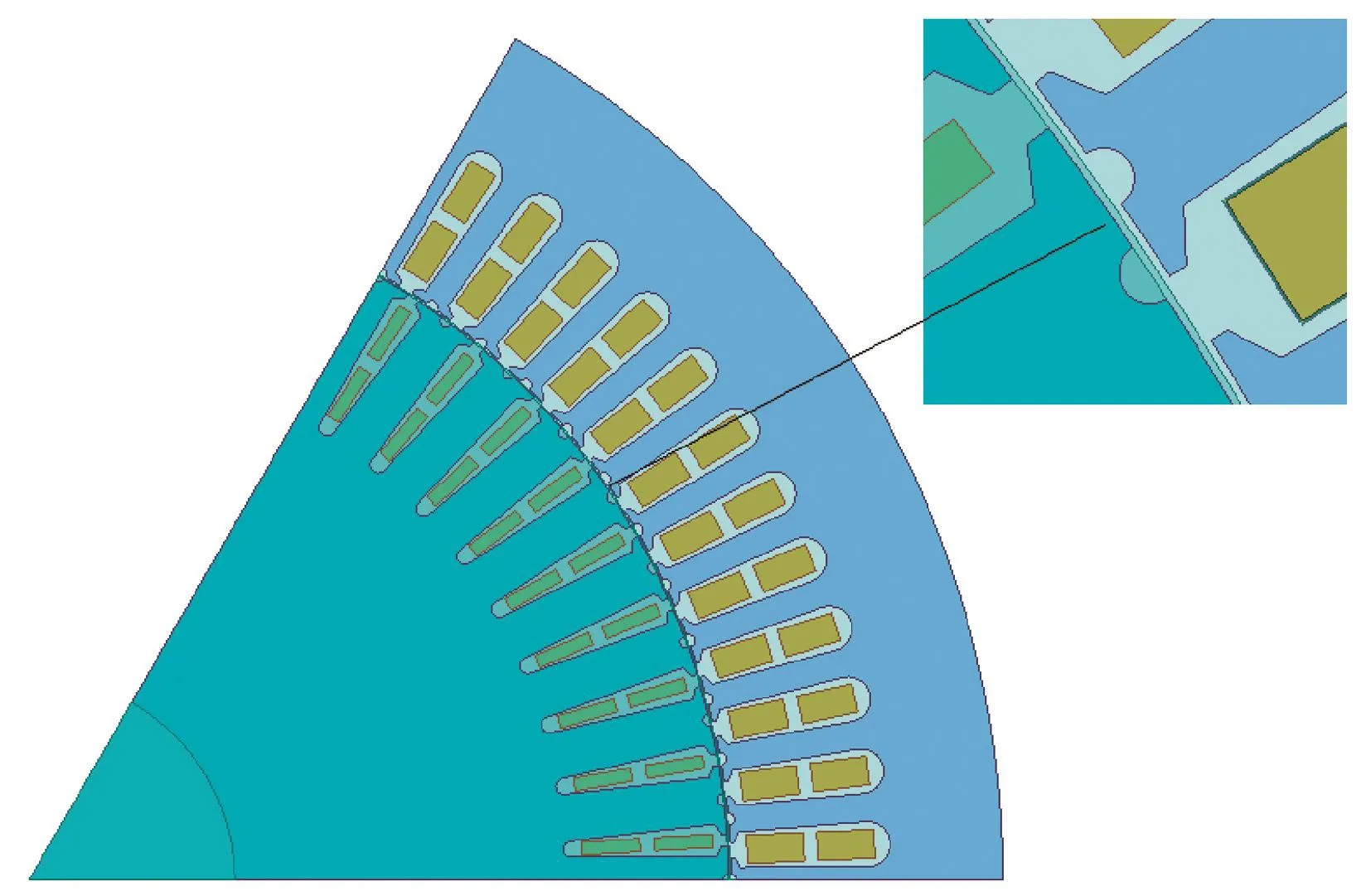
圖16 輔助槽局部放大

分別仿真分析定子斜槽 (1°～8°)，定子開半圓型輔助槽 (半徑1～2mm)、轉子開半圓型輔助槽(半徑1～2mm)。波形畸變率對比見表4。

表4 波形畸變率對比

電機的氣隙比磁導為:

式中，μ0為真空磁導率；δ為氣隙。

由上式可知，在定子上開輔助槽相當于降低電樞表面平均比磁導，雖然會少量增加勵磁磁勢，但可有效改善電樞磁勢波形，進而降低電壓波形畸變率。此方法可適用于不同齒寬，建議輔助槽直徑在0.5～0.8倍的定子槽寬范圍內選擇，本文所用樣機的定子槽寬為4mm。

由表4可知，在定子斜槽5°(一個齒距)和定子開半徑為1.2mm輔助槽 (輔助槽直徑為0.6倍槽寬)時波形畸變率最小，諧波得到有效削弱，說明這兩種方法對削弱齒諧波是有效的。

最后，將這兩種優化方法結合，重新進行有限元分析，得到空載電壓波形如圖17所示，諧波分布如圖18所示，此時波形畸變率為1.17%，此臺樣機得到了很好的優化。

圖18 優化后電壓波形諧波分布

4 結論

本文對一臺90kW可變速發電電動機樣機進行研究，利用有限元法分析其空載諧波特性，仿真表明，樣機的電壓波形畸變較大，超過標準要求的限值。分別考慮變流器諧波和電機本體齒諧波對空載電壓波形的影響。變流器諧波會導致電壓波形質量下降，通過對本臺電機齒諧波的研究，發現其齒諧波與轉差率和定、轉子的每極每相槽數相關。試驗對比有限元仿真的空載特性曲線和試驗的空載特性曲線基本一致，證明了有限元仿真的正確性。為改善電壓質量，本文采用定子斜槽、定子和轉子開輔助槽的方法大幅度降低了定子電壓的波形畸變率，優化結果表明，在考慮變流器諧波的影響下，諧波畸變率仍滿足標準要求。