基于決策樹算法的鋼板探傷預測模型優化

王復越 ，任毅 ，趙坦 ，崔福祥

（1.海洋裝備用金屬材料及其應用國家重點實驗室，遼寧 鞍山 114009；2.鞍鋼集團鋼鐵研究院，遼寧 鞍山 114009；3.鞍鋼股份有限公司鲅魚圈鋼鐵分公司，遼寧 營口 115007）

數字化研發手段賦能傳統工業領域可實現傳統產業轉型升級、提質增效以及先進產品研發創新能力的提升［1］。傳統鋼鐵制造行業各生產環節自動化程度高、數據量大、檢測數據完整性好，應用大數據技術可提升決策力、洞察力以及流程優化能力。鋼鐵行業在大數據技術方面的戰略意義在于對有價值信息數據進行專業化處理，也就是數據挖掘［2］。人工智能是進行大數據分析及數據挖掘工作的必然選擇，機器學習是實現人工智能的一種重要方式。目前機器學習領域已經發展出諸多適用于不同場景的機器學習算法，如決策樹、支持向量機、隨機森林、人工神經網絡以及最近發展迅速的深度學習等［3-5］。其中，決策樹算法因可進行可視化分析，生產規則易于理解和解釋［6］，在解決復雜、非線性、多變量、強耦合的工程問題上有明顯優勢，需要注意的是決策樹模型容易出現過擬合的問題［7］。經過這些年的發展，各類機器學習算法建模已與鋼鐵行業各環節的實際生產有著廣泛的結合，可應用于各類產品性能預測、失效預警與故障診斷當中［8-9］。

以管線鋼為例，其服役場景往往是復雜地形和惡劣環境，管線鋼鋼板在滿足各種服役力學性能的同時需兼顧良好的焊接性能、耐腐蝕性能。這對管線鋼鑄坯在高純凈度冶金與組織精細化控制方面提出了更高的要求［10］。然而在鑄坯的生產及軋制環節中物理與化學過程復雜，工況變化頻繁，生產過程中不可避免地引入非金屬夾雜物以及形成組織缺陷。鋼廠在后續的鋼板自動探傷檢測工序可將一部分存在問題的鋼板篩選出來，但由于鋼廠與制管企業以及管道安裝施工方在探傷設備與檢測方式等方面存在差異，時常出現鋼廠未檢出問題鋼板，但后續工序檢出的情況。此問題造成大批量鋼板退貨，給企業帶來大量經濟損失。

本研究基于上述問題與需求，采用CART決策樹算法建立預測模型，充分挖掘利用管線鋼鑄坯生產關鍵環節數據，通過模型結構調整與參數優化，達到模型預測水平的提升與泛化能力增強的目的。最終實現對管線鋼鑄坯的質量預判，降低問題管線鋼鋼板探傷檢測漏檢率。此外，本研究對于提升設備運行水平、提高產品質量以及降低不合格品退換貨帶來的經濟損失等方面都具有重要意義。

1 模型搭建

1.1 建模流程

本研究所涉及的決策樹模型是使用Python編程語言在Pycharm集成開發環境下建立并運行的，通過開源機器學習工具包Sklearn中的NumPy、Pandas等數值計算的庫來實現機器學習的算法應用。決策樹模型搭建步驟與流程見圖1。

圖1 決策樹模型搭建步驟與流程Fig.1 Building Steps and Flow Process for Decision Tree Model

結合冶金學原理，分析、篩選眾多生產工藝特征選項，將預測建模中的特征選項（features）設定為：RH處理周期、鋼中總鋁含量、RH凈循環時間、鋼液澆鑄過熱度、拉速、輥縫合格率。預測結果即標簽（Label）為鋼板探傷是否合格，合格為0，不合格為1。將生產數據中由于數據漏采集、傳輸設備信號故障、中斷等原因造成的數據缺失、亂碼等數據進行剔除處理，并以8∶2的比例將數據集隨機劃分為互斥的訓練集和測試集。特征數據集如表1所示。

表1 特征數據集Table 1 Data Set of Features

1.2 模型設定及優化方案

決策樹構建是通過選用不同的樣本純度度量指標（信息增益、增益率、基尼指數），找到包含關于目標特征的最大信息量（純度）的描述性特征，并沿著這些特征的值分割數據集，使得生成的子數據集中的目標特征值純度盡可能高，最終產生一個泛化能力強的判定流程模型［11］。為達到此目的，需要選定合適的樣本純度度量指標，設定決策樹深度（層數）以及葉子節點最小樣本數點。

本研究選擇基尼系數作為數據樣本的度量指標，在Sklearn機器學習工具包中Decision Tree Classifier模塊的Criterion設定中選定gini。為優化決策樹結構，分別設定決策樹最大深度為三層與四層，考察葉子最小樣本數從10到220條件下模型評估水平。隨后，對預測水平與泛化能力最佳的模型調整預測判定閾值，使模型對于探傷不合格鋼板的召回率達到70%以上的水平，且整體預測精準率不低于70%。此外，為平衡數據集中類別的失衡問題，根據數據集中探傷不合格鋼板比例設定樣本合格與不合格鋼板權重為1:19。

1.3 模型評價

對于所涉及的探傷結果二分類問題，可將數據中探傷結果樣例類別與分類器預測結果類別的組合劃分為真正例 （實際探傷不合格且預測正確）、假正例（實際探傷合格但預測錯誤）、真反例（實際探傷合格且預測正確）、假反例（實際探傷不合格但預測錯誤）四種情況，令 TP、FP、TN、FN分別表示其對應數量。使用ROC（Receiver Operating Characteristic）曲線描述分類器的預測能力及泛化性能的優劣，ROC曲線的縱軸是 “真正例率”（TPR），橫軸是“假正例率”（FPR），兩者定義為：

通過積分計算ROC曲線下面積（AUC）來，比對AUC數值大小實現對模型預測效果的評價，AUC值來表現其預測能力，訓練集與測試集AUC差值表現其泛化能力。AUC值越大，模型的預測能力越強，訓練集與測試集AUC差值越小，模型的泛化能力越好。

此外，以實際探傷不合格鋼板的召回率（Recall）為第一考察指標，并結合考察精準率（Accuracy）的方式對模型的實際預測水平進行評價。召回率與精準率的定義為：

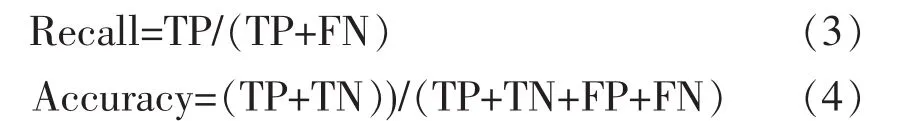
召回率可反映模型對于正例的預測水平，即對實際探傷不合格做出正確的判定，精準率則可以反映模型對正、反例的綜合預測水平。

2 模型優化

2.1 決策樹結構優化

本研究使用數據樣本中同一訓練集訓練決策樹分類器模型，分別設定決策樹模型最大深度為三層與四層，考察葉子最小樣本數從10到220條件下模型評估水平，葉子最小樣本數對預測模型AUC值的影響如圖2所示。

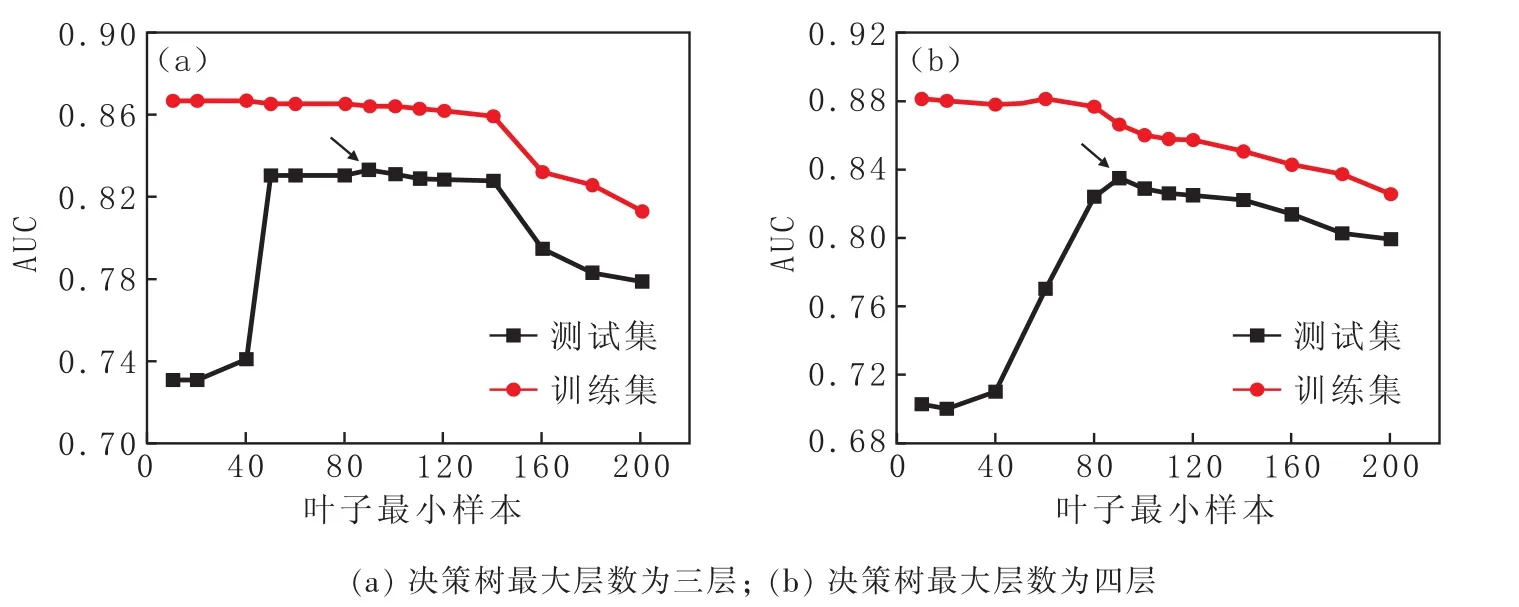
圖2 葉子最小樣本數對預測模型AUC值的影響Fig.2 Effect of Minimum Number of Samples of Tree Leaves on AUC Value of Prediction Model

從圖2（a）可以看出整體上訓練集AUC值高于測試集，訓練集AUC隨葉子最小樣本數變化的增大而小幅降低，而測試集AUC則在葉子最小樣本數為40時階躍上升，而后AUC一直保持較高的水平。直到葉子最小樣本數為超過140，測試集AUC下降明顯。當葉子最小樣本數為90時，測試集AUC值最大為0.833 9。在葉子最小樣本數相對較小時，經訓練集訓練的模型出現過擬合的情況，測試集AUC值較低，模型預測水平較低；在葉子最小樣本數設定相對較大時，所設定的模型結構規則無法很大的描述與反映數據特征，訓練集與測試集AUC值都在較低的水平，這說明模型出現了欠擬合的情況。同樣的，決策樹模型最大深度設定為四層時，訓練集與測試集AUC值隨葉子最小樣本數變化趨勢基本一致。訓練集AUC值在葉子最小樣本數為90時達到最高，為0.848 4。而后隨葉子最小樣本數的增大訓練集與測試集AUC值緩慢降低，如圖2（b）所示。從上述測試集AUC最大值以及隨葉子最小樣本數變化的情況看，該決策樹模型在最大深度為四層，葉子最小樣本數為90時，模型預測水平達到最佳。

決策樹模型訓練集與測試集ROC曲線如圖3所示。 從圖3（a）與圖 3（b）中可以看出，不同最大層數下代表訓練集與測試集的曲線都基本重合，最大深度為三層、四層時訓練集與測試集的AUC值差值分別為0.031 7、0.034 0。AUC差值都較小，這說明模型的泛化能力較好。

圖3 決策樹模型訓練集與測試集ROC曲線Fig.3 ROC Curves of Training Sets and Test Sets for Decision Tree Model

2.2 判定閾值調優

根據上文評估結果可知，經過結構優化后的決策樹模型具有較高的水平且模型泛化能力較強。然而在模型進行預測時需要設定一個預測判定閾值，模型生成預測分析值與其對比后才能進行合格與不合格的判定。通常判定閾值設定值較高時（接近1時），召回率較高，而精準率低；閾值設定值較低時（接近0時），召回率較低，而精準率較高。結合生產、檢測與供貨的諸多實際情況，建立“首先保證召回率”的模型判定的思想，同時兼顧考慮送檢鋼板數量與檢測能力的矛盾關系，對預測判定進行比對與調優。圖4為模型判定閾值對召回率及精準率的影響關系圖。

圖4 模型判定閾值對召回率及精準率的影響Fig.4 Effect of Decided Threshold Values for Model on Recall Rate and Accuracy Rate

從圖中可以看出，召回率隨判定閾值的增大而降低，精準率隨判定閾值的增大而提高，兩者呈相反的變化趨勢。當判定閾值小于0.4時，召回率約為80%，說明對大部分存在潛在問題的鋼板可完成召回。

結合模型在召回率與精準率的表現，設定判定閾值為0.4。為了更直觀的展示模型對訓練集與測試集的預測表現，將其對應混淆矩陣列出，如圖5所示。圖5（a）為以訓練集的混淆矩陣，召回率為85.3%，精準率為75.4%；圖5（b）為以測試集的混淆矩陣，召回率為74.0%，精準率為73.5%。此設定下模型在相對較小的檢測樣本中最大限度的完成不合格鋼板的預測與召回，同時模型對正、反例的預 測精準率均在70%以上，有效的利用了檢測資源。

圖5 訓練集與測試集混淆矩陣Fig.5 Confusion Matrix of Training Sets and Test Sets

3 決策樹可視化與分析

決策樹模型包括鋼中總鋁含量、RH凈循環時間、鋼液澆鑄過熱度、拉速、輥縫合格率的五點關鍵性生產指標，經過結構優化后的模型通過Graphviz.Source模塊實現對決策樹模型的可視化，圖6為管線鋼連鑄板坯探傷預測影響因素的決策樹模型。從圖6中可以看出，該決策樹模型共四層，共有9個節點，終端11個葉子節點。拉速是影響管線鋼連鑄板坯探傷結果最重要的影響因素，出現在決策樹的各層中。在實際生產中，通過調整連鑄拉速的方式來實現對生產節奏變化以及中間包溫度的配合與調節，其調節效果明顯，這也使得連鑄拉速波動較大。與此同時，連鑄拉速的波動對于鑄坯冶金質量的影響也是顯著的，拉速的變化關乎鋼液的動量傳遞、熱量傳遞與質量傳遞，影響熔體流動、液穴形態、凝固相變、結晶器壁面冷卻強度、“浮游晶”沉降、氣體與夾雜物上浮以及對耐火材料的溶蝕等多重方面［12］。因此，應嚴格控制連鑄拉速工藝波動，并設定連鑄拉速波動上限值，通過此方式可有效提高鑄坯與鋼板的冶金質量。

圖6 連鑄板坯探傷預測影響因素的決策樹模型Fig.6 Decision Tree Model for Influencing Factors of Flaw Detection Prediction of Continuous Casting Slabs

4 結語

基于工業生產數據，以煉鋼與連鑄環節多項關鍵工藝點為特征屬性，采用CART分類決策樹算法建立了中厚板連鑄板坯探傷預測模型。通過調整決策樹最大深度、葉子最小樣本數以及判定閾值，對決策樹結構與判定策略進行優化調整，經測試集驗證：優化后的決策樹模型對連鑄板坯對應軋后鋼板探傷結果預測具有較好的預測效果，AUC值為0.848，且模型泛化能力較強，訓練集與測試集AUC差值低于0.04。當判定閾值為0.4時，模型對測試集數據預測的召回率與精準率都高于70%，可實現對連鑄板坯探傷結果的高精度預測。此外，通過決策樹可視化分析可為工藝參數的調整與控制提供可靠依據。此項工作的開展有效提升鑄坯質量判定能力、大幅降低漏檢率，減低企業由于鋼板探傷不合退換貨帶來的經濟損失。為企業工藝智能化調節以及產品質量智能化管理提供幫助，對提高產品質量穩定性與工藝控制水平起到積極作用。