基于NAIS數據的交叉口車-車事故嚴重程度影響因素分析
肖樂
(1.西華大學 汽車與交通學院, 四川 成都 610039;2.汽車測控與安全四川省重點實驗室, 四川 成都 610039)
道路交叉口是多種交通流交匯與沖突的關鍵區域,是道路交通事故的多發地,研究道路交叉口事故嚴重程度影響因素對事故預防具有重要意義。牛志鵬等從道路條件、交通環境、安全設施管理三方面對道路平面交叉路口的交通安全進行了定性和定量分析。趙曉華等基于駕駛行為數據構建交叉口進口道安全性結構方程,挖掘風險因素,結果表明交叉口各方向車道總數、違法監控設備數量等對交叉口安全性具有顯著影響。呂通通等構建互信息貝葉斯網絡模型,分析了各影響因素變化與事故嚴重程度的定量關系。趙丹等構建雙變量Probit模型,以事故形態和事故嚴重程度為因變量,分析了農村交叉口交通事故的風險因素。Islam S.等建立隨機參數Logistic模型,對比分析了農村和城市道路中摩托車事故嚴重程度影響因素的差異性。溫惠英等以英國單車事故數據為樣本構建多項式Logit模型,分析了交叉口單車事故嚴重程度影響因素。Ariana Vorko-Jovic等研究了城市道路交通事故的發生及嚴重程度與人、道路、環境、道路信號燈設計、交通監管部門管理等因素之間的關系。上述研究多采用國外開源數據,難以反映具有中國特色的道路交通事故特征,且部分研究以國內某一城市的事故統計數據為研究對象,難以表征道路交通事故的共性。鑒于此,本文統計、分析國家車輛事故深度調查體系(National Automobile Accident In-Depth Investigation System,NAIS)中的交叉口車-車事故數據,研究道路交叉口事故嚴重程度影響因素,為交叉口事故預防提供理論支撐。
1 數據概述及變量描述
1.1 數據采集
NAIS由國家市場監督管理總局缺陷產品管理中心聯合8所具有較深事故研究背景的高校、事故鑒定機構及科研機構共同建立,其目的是采集具有中國道路交通事故特征的深度數據,并建立汽車主被動安全研究基礎數據庫。2011—2019年已收集4 000多起道路交通事故案例,覆蓋全國7個地區,包括東北、華南、西南、華北、華東等地。數據主要由交通事故采集人通過到事故現場復勘和交警部門獲得,包括事故照片、編碼的數據、警方資料、事故現場視頻、事故重構文件、CAD事故現場圖及事故分析報告等,數據完整、詳細,對交通事故研究具有較高價值。本文篩選交叉口(三枝、四枝)車-車事故數據共計556條,剔除并清洗信息記錄不全數據后,得到有效數據471條。
1.2 變量選取及說明
1.2.1 因變量
根據初始數據將事故嚴重程度分為4個等級,分別為輕微事故(僅輕傷)、一般事故(重傷,未死亡)、重大事故(死亡一兩人)、特大事故(死亡3人及以上),由于特大事故僅占0.002%,將其與重大事故歸為一類,最終將人員傷亡事故嚴重程度由低到高劃分為3個等級,分別為輕微事故(僅輕傷)、一般事故(重傷,無死亡)、重大事故(死亡1人及以上),頻數分別為40、210、221。因變量編碼及描述見表 1。

表1 因變量編碼
1.2.2 自變量
調研國內外學者對交叉口事故影響因素選取情況,結合原始數據事故特征,從駕駛員、車輛、道路、環境4個維度選取13個離散型變量作為自變量,分別為駕駛員主要過失、性別、天氣、事故發生時段、參與車輛類型、道路行政等級、路段類型、路口是否有信號燈、路面狀況、道路線形、路燈是否開啟、是否有交通限速標志、對向機動車道隔離形式。由于道路交叉口流量大、沖突多,車型構成復雜,車輛安全狀況參差不齊,選取8種車型共4類用于分析車輛類型的影響。結合歷年交叉口交通違法行為統計數據,選擇超速駕駛、酒后駕駛、未按規定讓行和其他違法操作分析駕駛員主要過失對事故特性的影響(見表2)。

表2 自變量設置說明
2 有序Logistic回歸模型構建
2.1 模型構建
有序Logistic回歸是針對有序多分類變量的一種統計分析方法,而交通事故嚴重程度預測是一個有序多級別劃分的非線性問題。設有序多分類變量Yi(i∈{1,2,…,n})有j個等級,取值為1,2,…,j,X為m個自變量x1,x2,…,xm,則有序Logistic回歸模型表達式為:
(1)
式中:P(Yi≤j|X)為累積概率,P(Yi≤j|X)=1;αj為常數項;M為自變量數量;βjm為回歸系數。
有序Logistic模型共有j-1個。有序Logistic的概率模型表示為:
(2)
2.2 模型適用性檢驗
2.2.1 變量的多重共線性檢驗
在進行模型擬合之前,采用方差膨脹因子對13個變量之間的共線性情況進行診斷。方差膨脹因子是容忍度的倒數,用于判斷是否存在多重共線性,其值為0~10表示可以接受。結果表明13個自變量之間無多重共線性(見表3)。
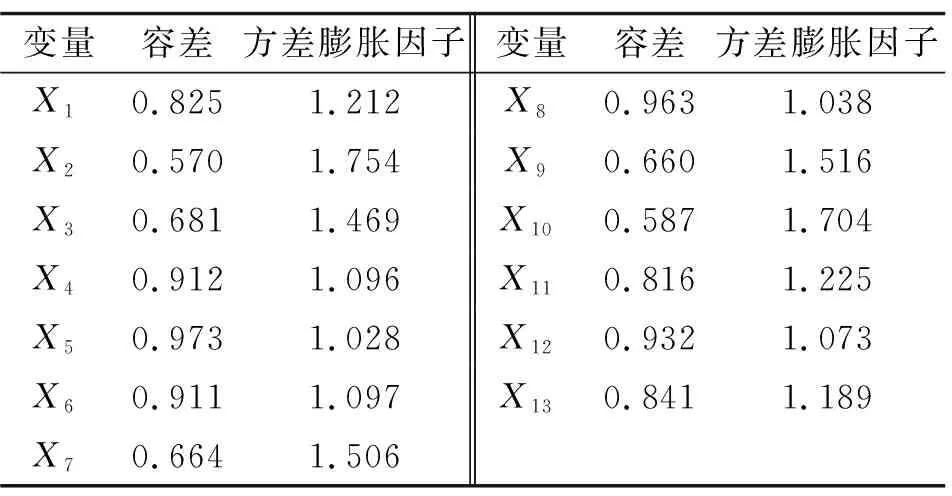
表3 變量的多重共線性診斷
2.2.2 平行性檢驗
平行性檢驗結果見表4。卡方值為24.636,顯著性P為0.369>0.05,接受原假設,有序Logistic回歸模型合適。

表4 平行性檢驗結果
2.2.3 PearsonX2檢驗和偏差統計量
PearsonX2檢驗通過頻數檢驗模型成立的假設,其標準X2統計量計算公式為:
(3)
式中:Ok為第k類協變類型的實際頻數;Ek為第k類協變類型的期望頻數;K為協變類型的種類數。
X2的自由度為協變類型數目與參數數目之間的差距,X2統計量的值越小,模型擬合效果越好。
在Logistic回歸模型中,將偏差統計量D視為擬合優度統計量,計算公式為:
(4)
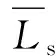
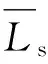
PearsonX2檢驗結果見表5。由表5可知:PearsonX2統計量的顯著性P為0.518,偏差統計量的P值為1.000,模型的擬合效果好。
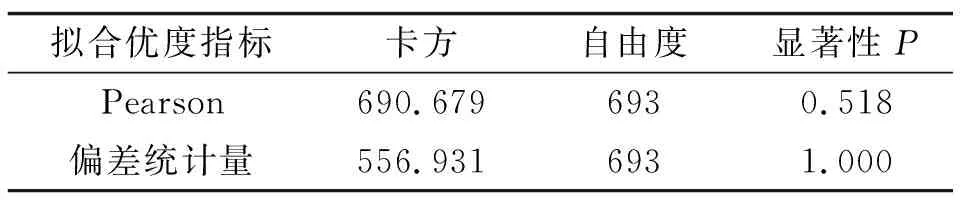
表5 Pearson X2檢驗結果
2.2.4 數據的單變量觀察
利用SPSS描述性統計中的交叉表,依次對13個指標與事故嚴重程度之間的關系進行卡方檢驗,檢驗結果見表6。由表6可知:路段類型、性別、路口是否有信號燈、道路線形、路面狀況、對向機動車道隔離形式與事故嚴重程度沒有顯著關系。自變量篩選過程中,結合模型的Wald檢驗結果,逐步剔除無統計學意義的自變量,剔除順序依次為路段類型、性別、道路線形、路面狀況、對向機動車道隔離形式。剔除過程中發現路口是否有信號燈的顯著性接近0.05,暫不予以剔除。
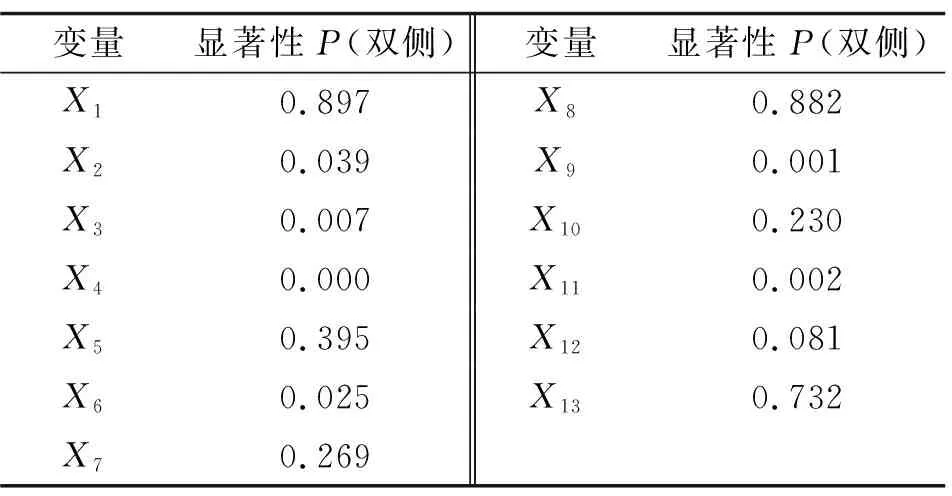
表6 單變量顯著性檢驗結果
3 模型計算結果分析
有序Logistic模型計算結果見表7。擬合優度檢驗中P<0.001,拒絕原假設,有序Logistic模型整體有意義。
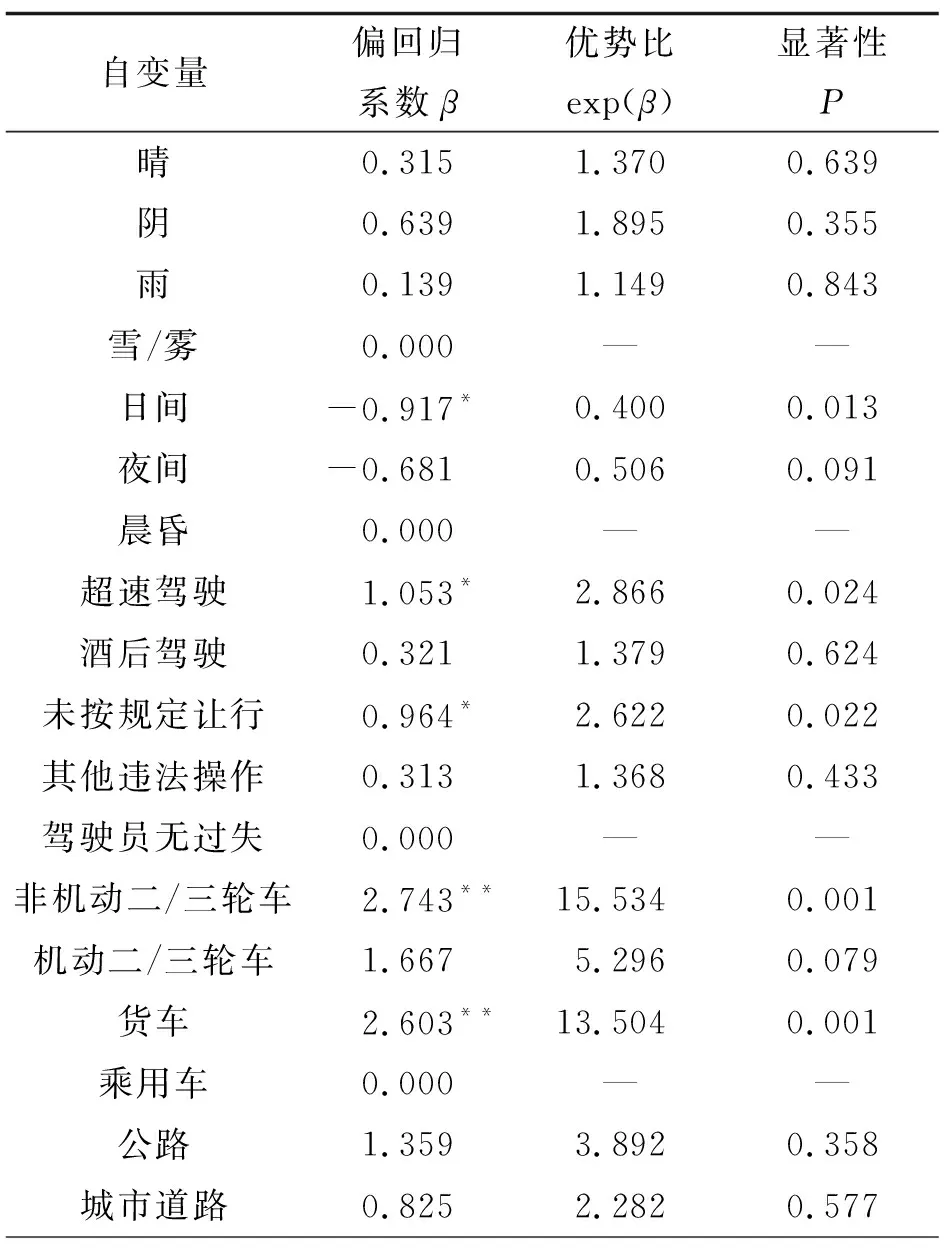
表7 有序Logistic模型估計結果
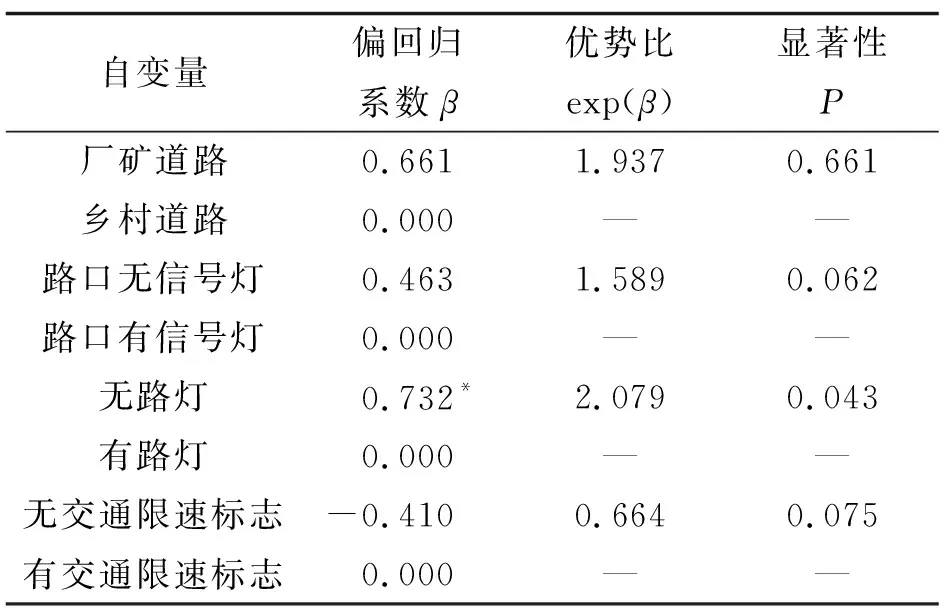
續表7
由表7可知:
(1) 駕駛員。駕駛員存在過失會對事故嚴重程度產生顯著正影響。以駕駛員無過失事故嚴重程度為參照,超速駕駛、未按規定讓行的偏回歸系數分別為1.053、0.964,超速駕駛對事故嚴重程度影響最顯著,其次是未按規定讓行,分別使交叉口事故嚴重程度上升286.6%、262.2%。
(2) 車輛類型。非機動二/三輪車和貨車對事故嚴重程度產生顯著正影響。以乘用車為參照,參與車輛涉及非機動二/三輪車的偏回歸系數為2.743,對事故嚴重程度影響最大;其次是貨車和機動二/三輪車,偏回歸系數分別為2.603、1.667。
(3) 道路。路口是否有信號燈、路燈是否開啟對交叉口事故嚴重程度產生顯著正影響。以路口有信號燈為參照,路口無信號燈條件下交叉口事故嚴重程度上升158.9%。以有路燈為參照,無路燈情況下事故嚴重程度上升207.9%。可見,完善的交通信號控制設施對降低事故嚴重程度極為重要。
(4) 環境。事故發生時段對事故嚴重程度有顯著影響。以事故發生時間為晨昏為參照,事故發生時間為日間的偏回歸系數為-0.917,與事故嚴重程度呈顯著負相關。相比于晨昏,日間發生的交通事故嚴重程度更輕,事故嚴重程度降低40%。
4 結論
以NAIS數據庫中交叉口事故數據為樣本,從人、車輛類型、道路、環境四方面選取13個變量構建有序Logistic回歸模型,分析車-車事故嚴重程度的影響因素,得出如下結論:1) 駕駛員過失、車輛類型、路口是否有信號燈、路燈是否開啟、事故發生時段顯著影響事故嚴重程度。2) 超速駕駛、車輛類型為非機動二/三輪車、貨車對事故嚴重程度影響最大;路口無信號燈、無路燈、事故發生時段也會使事故嚴重程度加重。
隨著NAIS體系中數據量的逐年增加,未來可以綜合更多的道路交叉口事故數據進行分析,以更準確地掌握交叉口車-車事故嚴重程度的影響機理。

