基于路網協同維護的災后配電網搶修優化研究*

馬傳奇，王國慶，于 雷，朱建明，黃 鈞

(1.中國科學院大學 工程科學學院，北京 100049；2.齊齊哈爾北車輛段，黑龍江 齊齊哈爾 161099；3.中國科學院大學 應急管理科學與工程學院，北京 100049)

0 引言

當今社會，電網成為人們賴以生存的基礎生命線設施[1-2]，極端災害造成的停電事件往往帶來巨大損失。近年來極端災害頻發，我國南方在2008年發生罕見冰雪災害，造成約170個縣市的大范圍停電事故，直接損失超過百億[3]；2017年美國遭遇Harvey颶風與Iram颶風,大量的配電網設施被損壞，導致約1 500萬用戶的停電[4]。因此，配電網的災后應急搶修工作具有重要研究價值。

極端災害不僅損壞配電網，也會對路網造成破壞。以往研究大多忽略路網損壞狀況，因配電網規模較小而忽略搶修途中的行駛時間[5]。但現實中，路網損壞常使配電網的應急搶修難以展開，如2021年7月的河南洪災中，道路中的洪水嚴重阻礙配電網的搶修工作[6]。因此，在配電網的災后搶修中，路網損壞狀況不能忽略，路網維護十分必要。

目前配電網的搶修研究中，常以最小化減負荷為目標，通過應急搶修與拓撲重構實現配電網的運行恢復。文獻[7]基于配電網的災后重構提出受損線路的復電路徑概念，研究多配電搶修隊協作搶修下的配電網快速復電問題；文獻[8]在最小化減負荷的目標下，利用SNOP在配電網故障期間維持不間斷供電和提高電能質量的靈活控制特性；文獻[9]針對災后非故障區域的負荷斷電狀況，在搶修過程中對開關刀閘進行重構,通過改變負荷的供電路徑使失電負荷盡可能恢復供電。

微電網在近些年成為配電網的災后研究熱點，其原理為孤島運行下，通過利用風能或太陽能等分布式電源維持微電網運行[10]。文獻[11]基于配電網的徑向分布，通過形成多個由分布式電源供電的微電網，以實現災后對關鍵負荷的供電；文獻[12]提出使用內燃機車輛作為微電網的能源，以在災后增強系統的靈活性；文獻[13]考慮到微電網內發電資源的可變性和稀缺性提出三級供電恢復方法，通過應急發電車和微電網來協同恢復所有關鍵負荷，并搶修各時期的非關鍵負荷來實現配電網的災后恢復。

文獻[14]建立的配電網彈性恢復物流中將災后道路分為可行和不可行，并進行配電搶修隊與分布式發電機的協作調度；文獻[15]建立加權動態分配模型用以刻畫路網實時狀態，對移動應急電源與配電搶修隊進行協同調度。然而，上述文獻在配電網的災后搶修中均沒有考慮路網維修的協同。因此，本文展開路網維護協同下配電網的災后調度搶修研究，并探索路網維護如何影響配電網的調度維修，以期找到路網維護與配電網維修之間的影響機制，為現實背景下災后配電網維修與路網維護的協同優化工作提供參考和借鑒。

1 問題描述與模型假設

極端災害發生期間，隨斷電用戶數量不斷增加，配電網性能不斷降低；災害結束時，性能降至最低；災害結束后，配電網的搶修工作展開，隨著損壞線路的不斷維修直至配電網完全恢復。極端災害發生后配電網的系統性能變化趨勢如圖1所示。

圖1 系統性能變化曲線Fig.1 Curve of system performance change

圖1中，R(t)為系統性能水平隨時間變化的度量；t0，t1分別表示極端災害發生時刻和配電網受損的開始時刻；t1～t2期間，隨斷電用戶數量增加，系統性能逐漸降低，直至災害結束的t2時刻下降至性能最低點Rmin；在t3時刻開始搶修配電網；至t4時刻，配電網完全恢復，此時斷電用戶都重新連接到公用電網；t4時刻之后，系統性能恢復到正常水平。

電網研究中常采用如圖2(a)所示的配電網接線圖，表示配電網的災后損壞狀況，其中損壞線路有0-1，3-4，4-5，其余為線路完好。本文將重構后依然連接在一起的失電負荷視為1個超級節點，表現為同時斷電、通電,可轉換為圖2(b)接線圖G′，表示超級節點的復電順序。圖2(b)中N1={1，2}表示由失電負荷1和2構成的超級節點，類似有N2={4，6}，N3={5}。應急倉庫及配電故障點(即超級節點)的位置可在地圖中獲得，路網狀況圖可通過無人機獲得。將應急倉庫和超級節點的位置耦合到路網中，形成如圖3所示的耦合路網狀況圖，其中2點間的道路有且僅有可行與損壞2種狀態。

圖2 配電網接線圖G，G′Fig.2 Wiring diagram of power distribution network G，G′

圖3 耦合路網狀況Fig.3 State of coupled road network

如果不考慮路網損壞，相較于損壞電路的維修時間，配電網搶修隊的行駛時間可忽略不計。假設本例僅有1支配電搶修隊，各超級節點的維修時間和權重都為1，P1,P2,P3分別表示超級節點N1，N2，N3的有功需求且分別為3，2，1。如果不考慮路網損壞狀況，此時基于P1>P2>P3與復電路徑，優化后的維修順序為N1-N2-N3；如果考慮路網損壞且耦合路網狀況如圖3，假設僅有1支路網維護隊，每條損壞道路的維護時間都為Tl，則此時基于P1>P2>P3、復電路徑以及損壞路網通行狀況，有Tl≤0.5時，配電網的最優搶修順序為N1-N2-N3，否則為N3-N1-N2。因此，配電網的調度維修中，損壞路網狀況不可忽略。

基于此，本文構建的模型包含路網搶修策略約束、配電網維修策略約束及配電網運行約束。假設災害發生后，配電網與路網的損壞狀況可以立即獲得；由于大約90%的災后配電網受損情景是線路損壞，因此假設配電網的損壞情景都為線路損壞；由于配電網規模小，假設可行道路的所需行駛時間可忽略不計[5]，損壞道路在被修好前不可行。

2 考慮損壞路網維修的災后配電網恢復策略模型

2.1 模型中的集合、參數、變量定義

模型的集合與標記、參數、變量的定義如表1～3所示。

表1 集合和標記Table 1 Sets and labels

表2 參數Table 2 Parameters

表3 變量Table 3 Variables

2.2 數學模型

2.2.1 目標函數

災害發生后，如醫院等重要用戶應被優先考慮恢復供電。配電網中，各節點通過消耗有功功率而工作，無功功率不被消耗。因此，假設配電網完全恢復至多花費的時間為T，則目標函數f為最小化加權減負荷，如式(1)所示：

(1)

2.2.2 路網搶修策略約束

路網搶修策略約束條件如式(2)～(11)所示。其中，式(2)表示路網維護隊在任意時刻至多維護1條損壞道路；式(3)表示任意損壞道路在維護時間不小于其所需要時間時才可行；式(4)表示任意損壞道路開始維護后的狀態，要么在維護中，要么被維護好；式(5)表示任意損壞道路最多被維修1次；式(6)表示任意道路的可行時刻在其被維護好之后；式(7)表示任意損壞道路一旦維護好就一直可行；式(8)表示非損壞道路一直可行；式(9)表示任意損壞道路被維護好之后才可行；式(10)表示任意損壞道路的維護調度開始時其處于被維護中；式(11)表示任意損壞道路一旦可行后就一直可行。

(2)

(3)

(4)

(5)

(6)

vmn,t≤vmn,t+1,?(m,n)∈Ed,t∈(1,T-1)

(7)

emn,t=1,?(m,n)∈EEd,t

(8)

emn,t≤vmn,t,?(m,n)∈Ed,t

(9)

γmn,t≤αmn,t，?(m,n)∈E,t

(10)

emn,t≤emn,t+1，?(m,n)∈Ed,t∈(1,T-1)

(11)

2.2.3 配電網維修策略約束

配電網維修策略約束條件如式(12)～(22)所示。其中，式(12)表示每個配電搶修隊在任意時刻僅維修1個超級節點；式(13)表示任意超級節點被維修的總時長不小于其所需時間才被修好；式(14)表示每個超級節點開始被維修后要么在維修中,要么被維修好；式(15)表示每個超級節點僅被維修1次；式(16)表示任意超級節點是否開始維修受其與上一維修點間的道路狀況限制；式(17)表示在配網拓撲上任意超級節點與前一節點的連通時刻在其被修好的時刻之后；式(18)表示任意超級節點一旦被修好就一直保持修好狀態；式(19)表示任意超級節點僅被修好后才能通電；式(20)表示任意超級節點的復電路徑約束，任意超級節點僅在其復電路徑集合均處于通電狀態后才能通電；式(21)表示任意超級節點的維修調度開始時其處于被維修中；式(22)表示任意超級節點一旦通電就一直保持通電狀態。

(12)

(13)

(14)

(15)

(16)

(17)

zm,t≤zm,t+1,?m∈Bd,t∈(1,T-1)

(18)

ym,t≤zm,t,?m∈Bd,t

(19)

ym,t≤yh,t,?m∈Bd,h∈Em,t

(20)

bm,t≤λm,t,?m∈Bd,t

(21)

ym,t≤ym,t+1,?m∈Bd,t∈(1,T-1)

(22)

2.2.4 配電網運行約束

配電網運行約束條件如式(23)～(32)所示。其中，式(23)～(26)分別表示變電站的有功功率，無功功率平衡；式(27)表示變電站的發電功率約束；式(28)表示配網節點的功率約束；式(29)表示損壞線路的視在功率約束；式(30)表示任意節點處的電壓約束；式(31)表示任意損壞線路的LinDistFlow潮流模型[16]；式(32)表示功率非負約束。

(23)

(24)

(25)

(26)

(27)

0≤Pi,t≤Pi,0≤Qi,t≤Qi,?i∈Vd,t

(28)

(pfij,t)2+(qfij,t)2≤ym,t(Sij,max)2,?lm=(i,j),t

(29)

(Vmin)2≤(Vi,t)2≤(Vmax)2,?i∈Vd,t

(30)

(31)

pfij,t≥0,qfij,t≥0,?i,j∈Vd,t

(32)

3 求解算法

本文采用Jacques F.Benders在1962年提出的Benders分解算法，其是1種用于解決混合整數規劃問題的常用算法。本文將其應用于求解路網—配電網協同搶修模型，并將所提的模型分解為主問題和子問題。

3.1 模型線性化

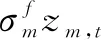
(33)

bmtn≤zn,t,bmtn≤emn,t,zn,t+emn,t-1≤bmtn

(34)

式(30)～(31)中的非線性是由于二次項造成的，可用ρi,t表示(Vi,t)2來消除二次項；式(29)中的二次項可以采用文獻[17]中的消二次項法，則式(29)可由式(35)表示：

(35)

3.2 子問題

(36)

s.t.式(23)～(28),式(30)～(32),式(35).

將上述問題轉化為對偶子問題(DSP)如式(37)～(46)所示：

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

(46)

3.3 主問題

對應的主問題(MP)如式(47)～(48)所示:

(47)

(48)

3.4 算法步驟

1)初始化上界UB=+∞，下界LB=-∞。

4)如果UB-LB≤Gap，迭代停止，否則構造1個形如式(48)的最優割平面(benders optimality cut)到主問題模型中，并轉向步驟2)，直到算法結束。

4 算法仿真

本文參照云南魯甸某地10 kV配電網構造的輻射型配電網案例，配電網簡化接線圖如圖4所示。圖4中有變電站1個，電力用戶24個以及分支節點4個。各電力用戶的權重相同且為1。變電站的最大輸出功率為6.6 MW，各用戶節點的功率需求按照其電氣接線圖變壓器的裝接容量計算。采用的電線均為LJG-50，參數設定為0.58 Ω/km，線路電阻按照實際距離計算。假設配電搶修隊有2支，1支和2支配電搶修隊搶修1條損壞線路的時間分別為7 h和4 h；路網維護隊有1支，每條損壞道路的維護時間相同且隨機選取[1,10]之間的整數，單位為h。

圖4 魯甸某地電網簡化接線圖Fig.4 Simplified wiring diagram of power distribution network in a region of Ludian

假設災后損壞的7條配電線路為1-2,4-5,10-11,13-14,18-19,15-16,24-26，配電網重構后形成超級節點N1～N7,對應的功率需求如表4所示，復電路徑如圖5所示。將應急倉庫和超級節點的位置耦合到路網中，形成如圖6所示的災后耦合路網狀況圖。

表4 超級節點的有功及無功功率需求Table 4 Active power and reactive power required by super nodes

圖5 超級節點復電路徑Fig.5 Power recovery path of super nodes

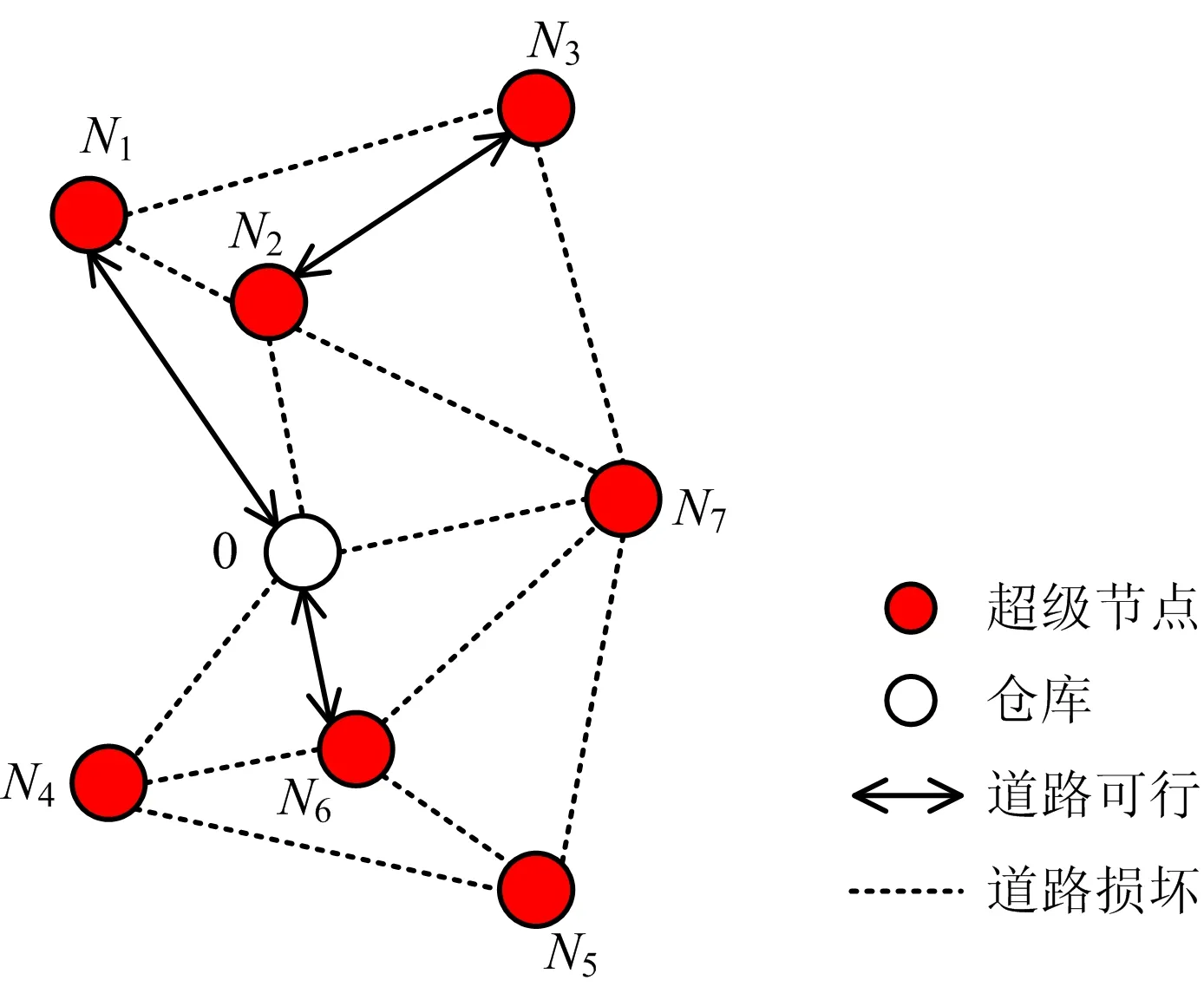
圖6 災后耦合路網狀況Fig.6 State of post-disaster coupled road network

假設每條損壞道路的維護時間相同并依次選取[1,10]內的整數，可得如表5所示的最優搶修順序安排和如圖7所示的配電網恢復時間的趨勢。

如果不考慮路網損壞，配電網的最優搶修順序為13-14，1-2，4-5，10-11，24-26，15-16，18-19，恢復時間為28 h。由表5和圖7可知，如果考慮道路損壞，最優搶修順序發生改變，說明道路損壞狀況不能忽略。且結合表5和圖7可以得到：1)道路維護時間為4 h是轉折點；2)道路維護時間在4 h及以內，配電網的最優搶修順序相同，在4～7 h最優順序不斷改變，在7～10 h最優順序相同；3)道路維護時間在4 h及以內時，配電網的恢復時間相同，在4～10 h恢復時間逐漸延長。

表5 配電網的最優搶修順序安排Table 5 Optimal rush-repair sequence arrangement of power distribution network

圖7 不同道路維護時間下的配電網恢復時間變化Fig.7 Change in recovery time of power distribution network under different maintenance time of road

本文將案例中的7步配電網搶修順序安排稱作7步時序安排，將考慮和不考慮路網損壞時的時序安排進行對照求出重合數，定義時序變異數=7-重合數，如表5中，當道路維護時間為4 h時，時序變異數為3。為避免上述案例結果的偶然性，其他條件不變下，假設每條損壞道路的維護時間都為4 h，各超級節點的權重可在{0.5,1}中隨機選取，可得128個案例構成的案例組，并定義每個案例的權重變異數為該案例中超級節點權重取值0.5的數量。運行后可得時序變異數隨權重變異數變化的分布情況如圖8所示，其中點(0,3,1)表示當所有超級節點的權重都為1時，與不考慮道路損壞相比，考慮道路損壞時的配電網維修時序變化數為3，且案例組中，時序變異數大于3的占據74.2%。因此進一步說明配電網的災后搶修中，路網維護的協同是必要的。

圖8 權重變化下時序變異數分布Fig.8 Distribution of time series variance under changed weight

5 結論

1)道路損壞會阻礙災后配電網的維修調度工作，因此在配電網維修期間，路網維護必不可少。

2)本文構建路網-配電網協同搶修模型，模型采用Benders求解算法，通過不斷生成最優平面以求得最優解，并通過案例驗證模型的有效性。

3)案例表明配電網的災后維修調度中，考慮路網的協同維護是必要的。配電網的恢復時間受到損壞路網的維護力量影響，隨著路網的維護力量提高，配電網的恢復時間先逐漸減小后趨于不變，因此，路網維護隊與配電搶修隊的力量配比很重要。當配電搶修隊的力量一定，如果路網維護隊的力量跟不上，配電網的恢復時間會被動延長；反之，路網維護隊的力量得不到充分利用。