基于邊權重圖神經網絡的一階邏輯前提選擇

劉清華，徐 揚，吳貫鋒，李瑞杰

（1.西南交通大學信息科學與技術學院，四川 成都 611756；2.西南交通大學系統可信性自動驗證國家地方聯合工程實驗室，四川 成都 610031；3.西南交通大學數學學院，四川 成都 611756；4.西南交通大學交通運輸與物流學院，四川 成都 611756）

自動推理作為計算機科學和數理邏輯的交叉學科，是人工智能的核心分支.一階邏輯（first-order logic，FOL）自動定理證明最初僅為了自動地證明數學定理，而目前已廣泛地應用于其他領域，例如電路設計、軟件驗證、硬件驗證和管理等[1-3].先進的一階邏輯自動定理證明器（automated theorem prover，ATP），如Vampire[4]和E[5]，擅長在TPTP （thousands of problems for theorem provers）[6]的某些限定領域中證明問題，但卻很難高效地證明大型問題庫中的問題（如，MizAR數學庫[7]）.這些大規模的問題被稱為大理論問題，其通常包含成千上萬個前提，但只有極少部分的前提能對問題結論的證明起到有效作用.

在FOL中，問題的前提和結論被形式化為一階邏輯公式.大多數ATP主要基于Given Clause算法[8]對從公式轉換而來的子句（合取范式）進行證明搜索.證明搜索是在兩個集合上執行：未處理子句集和已處理子句集.在證明搜索開始前，所有輸入子句都是未處理的.Given Clause算法反復地從未處理子句集中選擇一個子句作為給定子句，并將所有可能的推理規則應用于該子句和已處理子句集中的其他子句； 最后，新選擇的給定子句被放入已處理子句集中，新生成的子句被置于未處理子句中.此證明搜索過程將一直持續直到超出計算資源限制，或推斷出空子句或已處理子句集變得飽和（無法推斷出任何新子句）.

傳統ATP在證明大理論時，由于問題包含了數量極多的前提，在上述證明搜索的過程中，搜索空間會呈爆炸型增長.因此，計算機資源會很快地被耗盡，進而導致ATP證明問題的性能大幅降低.該問題導致了ATP無法在證明大理論問題時充分發揮作用.解決該問題的一種有效方法是在ATP試圖找到結論的證明之前，盡可能地選擇出最可能參與證明構造的前提.該過程被稱為前提選擇，通常作為ATP預處理的一部分，其對解決大規模問題至關重要.

起初，前提選擇通常采用基于公式中符號的啟發式方法[9-10]，主要通過計算和比較公式中的符號，對公式的相關性進行分析.最近，結合傳統機器學習技術[11-13]的前提選擇模型展現了具有競爭力的結果，但基于傳統機器學習的前提選擇在編碼邏輯公式時強烈地依賴于手工設計的特征（如，符號和子項等）.因為深度學習方法，如長短期記憶神經網絡（long-short term memory，LSTM）[14]和圖神經網絡（graph neural network，GNN）[15-17]，在編碼邏輯公式時不需要依賴于任何人工設計的特征，得到了越來越多學者的關注.又因為邏輯公式可以自然而然地表示為能夠保留公式句法和語義信息的有向無環圖（directed acyclic graph，DAG），所以定理證明與GNN的結合是當前最熱門的研究主題之一.

目前，主流的圖神經網絡框架通常通過聚集鄰接節點的信息來更新目標節點的特征表示.在此框架下的圖神經網絡模型常用于處理無向圖，如圖卷積神經網絡（graph convolutional network，GCN）[18]、圖注意力神經網絡（graph attention network，GAT）[19]等.然而，公式圖是有向，當前的圖神經網絡模型只能單向地沿著公式圖的邊進行信息傳播.除此之外，邏輯圖中相應的子節點之間是有順序的，而目前的圖神經網絡模型的信息聚集操作通常與子節點的順序無關.為發揮邏輯公式圖表示的優勢，理想的方法是根據公式的特性對公式圖中的節點進行排序并雙向地傳遞鄰接節點的信息.

針對上述問題，提出一種帶有邊類型的雙向圖用于表示一階邏輯公式.圖中相鄰的兩個節點由不同方向的兩條邊連接且每條邊都有一種對應的邊類型.通過確定每條邊特定的邊類型，可以對雙向圖中的節點進行排序.基于新的公式圖表示，提出了一種基于邊權重的圖神經網絡模型，即EW-GNN （edgeweight-based graph neural network）.對圖中的每一個方向，EW-GNN首先利用節點的信息更新對應邊類型的特征表示，隨后利用更新后的邊類型特征計算鄰接節點對中心節點的權重.傳遞給中心節點的信息是鄰接節點信息的加權和.EW-GNN最后匯聚中心節點來自兩個方向上的信息，并對節點進行更新.實驗比較分析表明：當前主流模型在測試集上的分類準確率兩兩之差均小于1%，而提出的EW-GNN在相同的測試集上比表現最優的模型還能提高約1%的分類準確率.因此，EW-GNN能夠在前提選擇任務中表現得更加優越.

1 一階邏輯公式圖表示

1.1 一階邏輯公式

在一階邏輯中[20]，給定一個變量符號集 V，一個函數符號集 F，以及一個謂詞符號集 P.一階邏輯項（term）是一個變量項v∈V或者形如f(t1,t2,···,tn)的函數項，其中，f∈F為n（n≥0）元函數符，t1，t2,···,tn是項.一階邏輯原子（atom）形如P(t1,t2,···,tn)，其中，P∈P為n（n≥1）元謂詞符.一階邏輯公式是由一階邏輯聯結詞 C={～,∧,∨,→,?}、量詞 Q={?,?}和原子聯結而成.

1.2 圖定義

帶有邊類型的雙向圖定義為G=(V,E,RE)，其中：節點集V={v1,v2,···,vn} 包含G中所有節點；邊集E={〈vi,vj〉|vi,vj∈V} 包含G中所有邊，有向對eij=〈vi,vj〉 表示從節點vi到節點vj的有向邊；邊類型集包含G中所有邊對應的邊類型.節點vi的鄰接節點集定義為 N(vi)= {vj|eji∈E}.圖中的每一個節點v都伴隨著一個初始節點特征向量xv∈Rdv，每一條邊e也伴隨著一個初始邊特征向量xe∈Rde，表示其對應的邊類型.dv和de分別為xv和xe的初始向量維度.

1.3 表 示

一階邏輯公式能夠自然地表示為語義解析樹（abstract semantic tree，AST）.通過添加從量詞節點指向到相應被約束的變量節點的邊以及合并所有相同的子表達式對應的子樹，可以將表示公式的AST擴展為含有根節點的DAG.

為了保持邏輯公式圖中部分節點之間有序性以及雙向傳遞鄰接節點的信息，設計了雙向圖表示，其中圖中相鄰的兩個節點由方向不同的兩條邊連接且每條邊都具有一種對應的邊類型.

邏輯公式圖中的節點大致可分為5種類型：量詞、邏輯聯結詞、謂詞、函數和變量.在定義邊類型時，邏輯連接詞節點、量詞節點和特殊的相等謂詞（=）節點的名稱為其類型，而其他謂詞、函數以及變量節點的類型為其對應的類型，分別記為pred、func和var.

然而，對邏輯公式圖中的子節點進行排序仍是一個難題.利用文獻[16]中提出的排序方案，從上往下單向地定義節點順序，即在給定相應父節點類型的情況下，對其子節點進行排序：

1）如果父節點是邏輯聯結詞 ～、∧、∨、? 或 =，則它們對應的子節點的順序一樣；

2）如果父節點是量詞 ? 或 ?，則其變量子節點具有相同的順序，而其他子節點是線性排序的；

3）如果父節點是其他謂詞、邏輯連接詞或函數，則其子節點是線性排序的.

正式地，一階邏輯表達式s的雙向圖表示Gs=(Vs,Es,Rs)構造如下：

1）如果s是一個變量項或常量項（0元函數項），則Vs={s}，Es={?}；

2）如果s=f(s1,s2,···,sn)，其中，f∈F∪P∪C且s1,s2,···,sn為子表達式，則，其中，H(si)為表達式si的最外層符號.如果s包含相同的子表達式，則在Gs上合并（merge）相同的子圖；

3）如果s=，其中， ?∈Q，是包含變量x的表達式，則Vs=Vs?∪{?}，Es=Es?∪{〈?，H()〉}∪{〈H()，?〉}∪{〈?,x〉}∪{〈x,?〉}.隨后，在Gs上合并所有由量詞 ? 約束的變量x；

4）在遞歸構造完Gs后，用統一的標記 * 更替Gs中所有變量節點的名稱；

5）Rs中的每一個邊類型由對應連接的兩個節點的類型和節點順序決定.

圖1為一階邏輯公式 ?x,y(p(f(x),a)∨q(a,f(y)))的雙向圖表示，其中：y(?)為變量；p(?)和q(?)為謂詞函數；f(?)和a分別為一元函數和零元函數（常元）.

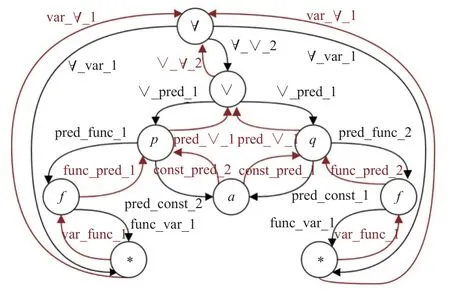
圖1 一階邏輯公式的雙向圖表示Fig.1 Bidirectional graph representation of first-order logical formula

在圖1中，變量節點x和y被替換成了統一的標記 *，替換后的雙向圖能在變量更名下保持一致.兩種不同顏色的邊分別代表了圖中兩個不同的方向.與單向圖相比，雙向圖中的每個節點有來自兩個方向上鄰接節點，如 ?、P和Q都是圖中的節點 ∨的鄰接節點.通過給圖中的邊添加類型，可以在一定程度上對圖中的相關節點進行排序.如在節點 ? 下，變量節點x和y（即節點*）的順序相同且記為1，因此節點 ∨ 的順序自然地記為2.連接節點 ? 和 ∨ 的兩條邊上的順序均為 ∨ 在從上到下的單向圖的中作為 ? 的子節點的順序.除此之外，邊類型同樣也反映出了邊的方向.邊類型 ?_∨_2和 ∨ _?_2分別表示從節點 ? 指向節點 ∨ 的邊和從節點 ∨ 指向節點 ? 的邊.

2 模 型

所有前提選擇模型都具有相似的框架，即，對邏輯公式進行表示并計算公式間的相關性.其正式定義如下：

定義1[11]給定一個結論c和其前提集A，前提選擇需要預測并選擇A中可能對證明c有用的前提.

如圖2所示，一個完整的端到端基于圖神經網絡的前提選擇模型應包含以下3部分：公式圖表示、圖神經網絡模型和二元分類器.在本文中，首先，將一階邏輯公式轉化為帶有邊類型的雙向圖；其次，通過使用新提出的EW-GNN模型，將邏輯公式圖編碼為特征向量；最后，二元分類器將一個結論向量和一個候選前提向量的拼接作為輸入，并輸出一個 [0,1]之間的實數得分，該得分表明在證明結論中使用候選前提的概率.

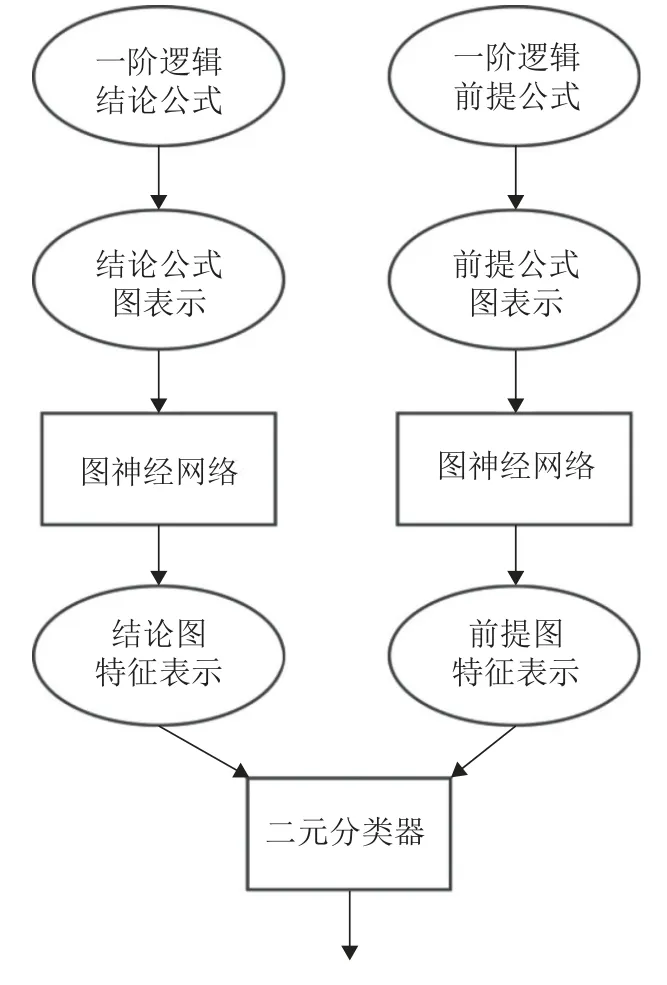
圖2 基于圖神經網絡的前提選擇模型Fig.2 Premise selection model based on graph neural network

給定一個大理論問題和訓練后的前提選擇模型，可以將所有的{結論,前提}對反饋給前提選擇模型，并輸出每個前提對結論有用（無用）的概率.根據輸出的概率，可以對前提進行排序，并從排序中選擇出前np個前提作為給定結論的有用前提.最后，ATP將使用np個選定的前提自動地證明對應的結論，從而解決ATP搜索空間爆炸增長的問題.

2.1 基于邊權重的圖神經網絡

EW-GNN模型包括4個階段：初始化、消息聚合、消息傳播（節點更新）以及圖聚合.

在初始化階段，模型通過不同的嵌入函數Fv和Fe將任意初始節點特征向量xv和初始邊特征向量xe分別映射為初始節點狀態向量和初始邊狀態向量：

Fv和Fe在本文中被設計為不同的查找表，用于存儲固定字典和大小的嵌入，并將用熱獨（one-hot）向量表示的xv和xe分別編碼為固定大小的初始狀態向量.

在第k（k=1,2,···,K）次信息聚集階段，EWGNN根據邊的方向，分別聚集目標節點vi來自兩個方向上的鄰接節點vj的信息.這里，簡單地把邊的方向分為從上往下和從下往上.為計算vj對vi的權重，首先利用vj和vi第k? 1次狀態向量和，以及第k? 1次邊狀態向量對第k次邊狀態向量進行更新：

如果eji的方向是從上往下的，則

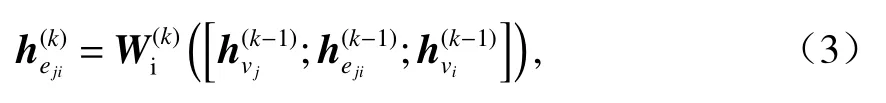
如果eji的方向是從下往上的，則

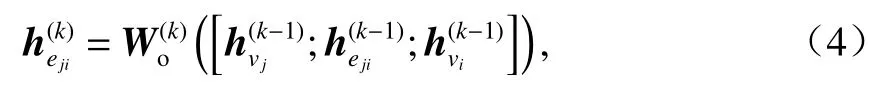
利用更新后的邊狀態向量，領接節點vj對中心節點vi的權重的計算如下：

如果eji的方向是從上往下的，則

如果eji的方向是從下往上的，則

節點vi來自鄰接節點vj的聚合信息為

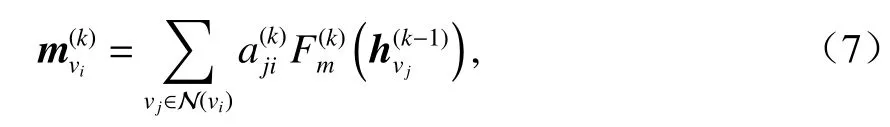
eji的方向不同，也隨之不同：

如果eji的方向是從上往下的，則

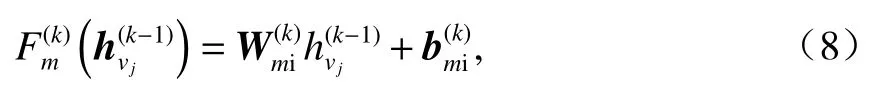
如果eji的方向是從下往上的，則

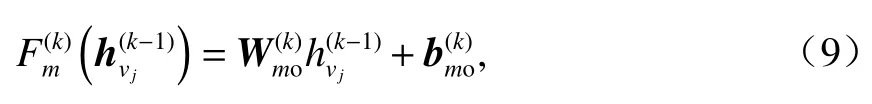
因此，節點vi的狀態向量的第k次更新為

第K次迭代后，EW-GNN在圖聚合階段對圖中所有節點狀態向量進行池化，以生成最后的公式圖向量：

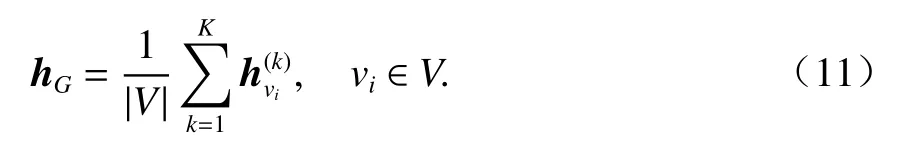
這里，采用了平均池化對整個節點維度上的節點特征求平均值.

2.2 二元分類器

分類模型的輸入是圖向量對 (hconj,hprem)，分別表示結論和候選的前提.EW-GNN通過分類函數Fclass對前提在結論證明中的有用性進行預測：

Fclass在本文中被設計為多層感知機（multi-layer perceptron，MLP）.具體為

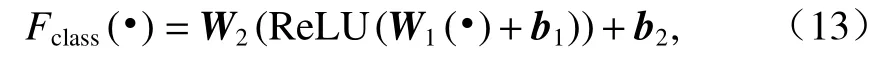
式中：W1∈Rdhv×R2dhv和W2∈R2×Rdhv為不同的學習矩陣；b1∈Rdhv和b1∈R2為學習偏差向量.ReLU(?)為修正線性單元（rectified linear unit，ReLU）函數：

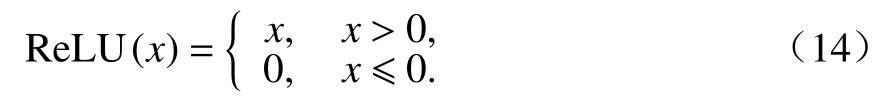
因此，前提在兩個類別下的預測概率為

2.3 損失函數

在均衡數據集下，對于每一個{結論,前提}對，損失函數 L 定義為預測值和真實值y之間的交叉熵：

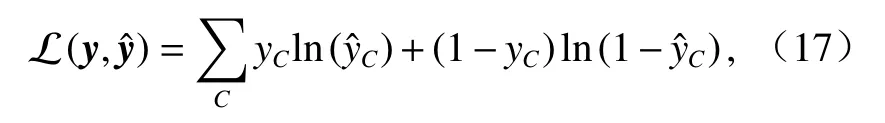
式中：y為真實值的一個獨熱編碼；yC和分別為真實值y和預測值在第C類別下的對應值.

在非均衡數據集下，對于每一個{結論，前提}對，損失函數 L 定義為預測值和真實值y之間的加權交叉熵：

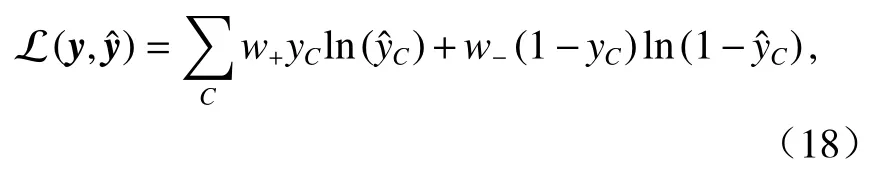
式中：w+、w?分別為正、負樣本的權重，且w+>w?.

在本文的模型訓練中，w+和w?分別設置為

式中：NP、NN分別為數據集中正、負樣本的數量.

3 數據集

本文基于MPTP2078問題庫[11]建立了一個用于訓練、驗證和測試前提選擇模型的數據集.

MPTP2078問題庫中一共包含2 078個問題，均來自Mizar數學庫（Mizar Mathematical Library，MML）[21]中與Bolzano-Weierstrass公理相關的問題.問題庫所有問題的前提和結論均被TPTP系統形式化為一階邏輯公式，且公式按照它們在Mizar數學庫中出現的順序線性排序.即，出現在每一個結論之前的公式（前提和其他結論）均可作為證明該結論的前提.問題的前提數量在區間[10, 4563]中，且前提的平均數量為1 876.表1具體地描述了問題庫中結論和前提的情況.

表1 MPTP2078問題庫描述Tab.1 Description of MPTP2078 benchmark條

數據集中每一個例子是一個三元組{結論,前提,標簽}.其中：前提是給定結論的候選前提，標簽是二元分類中的類別；標記為1的樣本記為正樣本，表示前提對結論有用；標記為0的樣本記為負樣本，表示前提對結論無用.在問題庫中，ATPboost[13]證明了1469個結論并一共產生了24087個證明，這意味著一個結論可能對應多個證明.

正式地，每一個被證明的結論c有nc（nc≥1）個證明P1，P2,···,Pr,···,Pnc，且Pr={pr1,pr2,···,prt,···,prncr}，其中：prt為構造證明Pr的一個前提，ncr是Pr中有用前提的總數.因此，有用前提集 UP(c)=包含至少在結論c的所有證明中出現一次的前提.

在數據集的構造中，對每一個已證明結論c，其對應的正樣本中的前提來自 UP(c).因此，結論c對應的正樣本為 (c,p,1)（?p∈UP(c)）且正樣本的總數為 |UP(c)|.

然而，問題庫中極大部分結論都對應了一個大規模的前提集且 UP(c)包含的有用前提數量僅僅只占總前提數量非常小的一部分.例如，MPTP2078問題庫中的結論 t12_yellow_6一共包含3836個前提，但只有5個前提被用于證明結論.這表明結論對應的無用前提數量遠遠大于有用前提數量.因此，如果使用c的所有無用前提來構造負樣本，則正負樣本的分布將極度不平衡.

為構建與正樣本數量相等的負樣本，使用文獻[22]設計的手工特征表示公式，并使用K近鄰（K-nearest neighbor，KNN）[23]算法粗略地對結論的所有前提進行排序.隨后，選擇對結論無用但排名靠前的前提構造負樣本，其中，無用前提的數量和有用前提大致相同.最終，整理得到的數據集如表2所示.

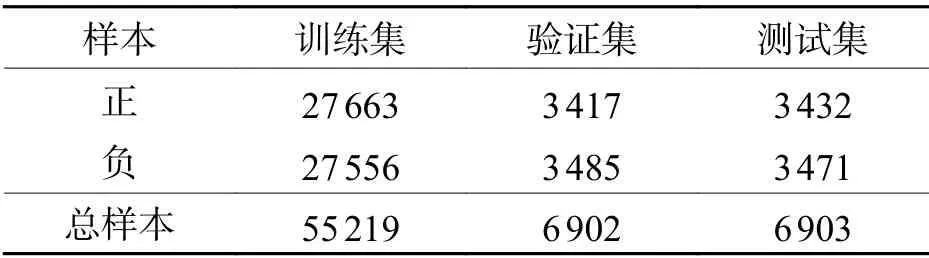
表2 數據集劃分Tab.2 Division of datasets個

4 實驗結果與分析

本文使用Python編程實現了本模型.在模型搭建的過程中，使用Pytorch庫[24]進行深度學習算法的實現，并使用Pytorch_Geometric庫[25]處理數據和對實現文中提及的所有圖神經網絡.本次實驗在超微4029GP-TRT服務器上進行，具體軟硬件配置環境如下：CenterOS7.6 X64，Intel至強銀牌4114，256 GB內存，2 TB SSD, 所用GPU為NViDIA RTX 2080Ti.

4.1 實驗參數

使用Adam[26]優化器對模型進行訓練.初始化的學習率為0.0010，在50個訓練輪次后，學習率衰減為0.0001.在每個輪次后，對模型進行保存并在驗證集上進行評估.經過所有輪次的訓練和驗證后，選擇在驗證集上表現最佳（損失最小）的模型作為最優模型，并在測試集上對其進行評估.為了保證實驗結果的公平性，文章中所有涉及到的模型參數設置均一致.具體參數如表3所示.

表3 參數設置Tab.3 Setting of parameters

4.2 評價指標

為評估所提EW-GNN模型的性能，將該模型與具有代表性的圖神經網絡模型進行比較.在前提選擇任務中，需要根據模型的輸出概率對前提進行排序.因此，需要同時評估正、負樣本的正確預測率.若僅關心正樣本的正確預測率，則過多的負樣本被錯誤預測為正時會嚴重地影響前提的排序，即無用的前提可能會在排序的前列.當數據集中正、負樣本分布均衡時，本文選擇準確率Accuracy指標對模型進行對比分析.Accuracy代表模型判斷當前前提對給定結論是否有用的準確程度：

式中：Total為數據集中所有樣本的數量；TP為分類正確的正樣本的數量；TN為分類正確的負樣本的數量.

本文同時增加召回率Recall、精確度Precision和F1指標F1對模型進行評估：

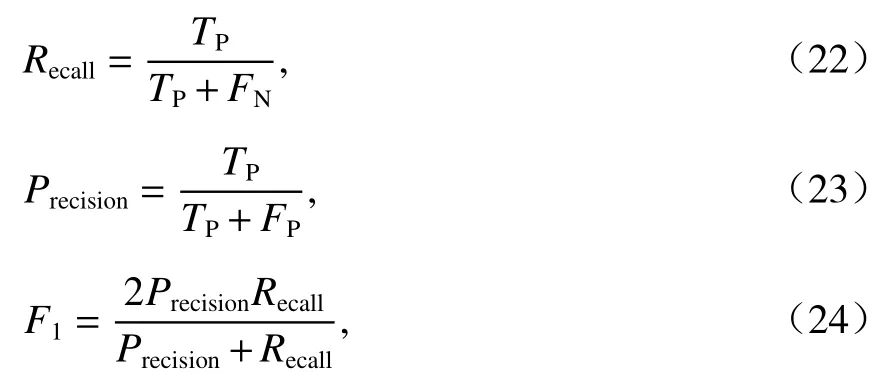
式中：FN為分類錯誤的負樣本的數量；FP為分類錯誤的正樣本的數量.

4.3 實驗結果分析

為保證對比結果的有效性，實驗過程中，只改變前提選擇模型中圖神經網絡模型的部分，而不改變初始化模型以及二元分類模型.所有方法在均衡數據集上的評估結果如表4所示，最佳結果以黑體突出顯示.

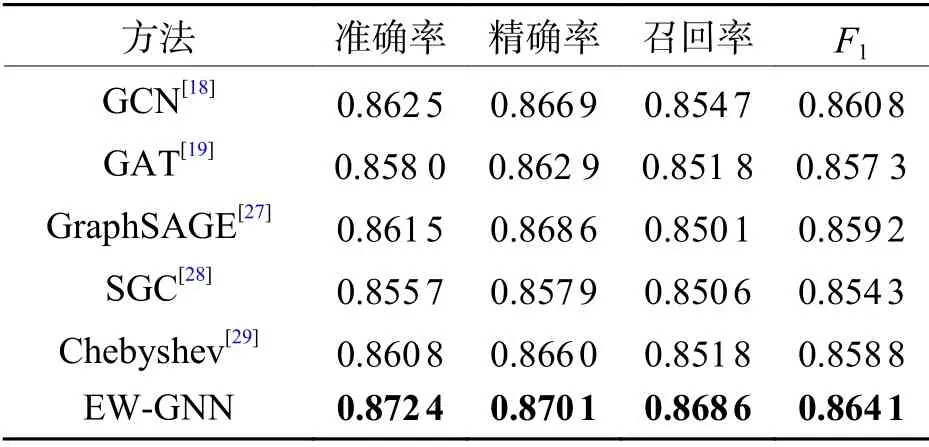
表4 數據集上的對比實驗結果Tab.4 Comparision of experimental results on datasets

實驗結果表明，所提出的基于邊權重的圖神經網絡EW-GNN在前提選擇任務中明顯優于目前其他流行的圖神經網絡模型：EW-GNN在相同的測試集上至少提高了1%的分類準確率.從表3中可以看出：除了本文提出的EW-GNN模型，沒有另一個模型的分類準確率能夠高于其他模型1%.這說明雙向地傳播鄰接節點的信息有助于幫助圖神經網絡模型生成更有表征能力的邏輯公式圖向量.EW-GNN在更新節點狀態向量之間，會首先對邊狀態向量進行更新.根據對邊類型的構造，邊向量既能反映由對應邊連接的節點類型，也能反映出節點的順序.這對表征一階邏輯公式非常重要.因為在一階邏輯公式圖中，不同類型的鄰接節點對中心節點的貢獻度是不同的.直覺地，函數節點的貢獻明顯要大于變量節點，因為變量在一階邏輯公式的表征中通常都被忽略.同樣地，節點的順序同樣也是邏輯公式圖表征不可忽略的重要特性.如，?xp(x,a) 和 ?xp(a,x) 是兩個不同的邏輯公式，如果忽略了x和a的順序，會導致這兩個邏輯公式最終生成的圖向量是一樣的.因此，EW-GNN根據更新后的邊狀態向量為中心節點的每個鄰接節點賦予權重，更加符合一階邏輯公式的特性.相比之下，本文所提出的EW-GNN模型更加適用于一階邏輯中的前提選擇任務.

5 結 論

1）本文針對一階邏輯公式的特性，提出了雙向圖表示方法，并對每條邊設計了能夠表示對應節點類型和順序的邊類型.

2）根據雙向圖的特性，本文設計并實現了一種基于邊權重的圖神經網絡模型EW-GNN.該模型既能夠雙向地傳播節點信息，也能利用邊向量編碼對應節點的類型和順序.

3）與當前流行的圖神經網絡模型相比，本文提出的模型明顯在前提選擇任務中更具有優勢.

4）針對一階邏輯公式的特性，未來計劃提出更加具有針對性的表征學習模型.