基于神經網絡的磁場定位技術

王華英，孫海軍，張雷,2,3，王學,2,3，黃艷賓,2,3，郭海軍,2,3

(1.河北工程大學 數理科學與工程學院，河北 邯鄲 056038；2.河北省計算光學成像與光電檢測技術創新中心，河北 邯鄲 056038；3.河北省計算光學成像與智能感測國際聯合研究中心，河北 邯鄲 056038)

受室內和煤礦地下等環境定位需求的推動，復雜環境下定位的相關技術研究備受關注[1-6].早期磁場定位方法大多為將磁源等效為磁偶極子陣列或橢球陣列，通過各點測量值建立線性方程組，然后反解出磁源的磁矩、位置等信息[7-17].但此種方法并不適用于空間含有不規則磁介質的環境，如煤礦井下掘進和綜采環境， 因此，面對煤礦井下掘進機截割部的定位難題，提出一種適合礦下環境的定位方法十分迫切.本文提出一種基于神經網絡的磁場定位算法，把含有大量不規則分布的鐵磁介質環境中的磁場定位問題等效為一個對高復雜性數據進行高維非線性擬合的問題，使用神經網絡完成高維非線性擬合，獲得空間磁場分布與磁源位置之間的映射關系，從而對目標進行定位[18-21]，并通過實驗研究了磁源移動步長及傳感器數量對定位精度的影響.

1 磁源定位系統建模

根據電磁場理論，當空間某點磁場位置確定時，它的磁場分布也隨之確定.反過來，當測得磁場在空間的分布時，產生磁場的磁源位置就是確定的.磁場強度可用三軸磁場傳感器測定.實驗時首先對所用磁場傳感器進行標定，將傳感器放置到正式實驗所設定的位置上，測量地球和環境磁場隨時間的變化，并保存下來作為背景磁場.然后把磁源放在實驗臺上，再利用磁場傳感器采集空間磁場數據，磁源每移動1步，記錄1次磁源位置坐標及磁場數據，直到磁源移動范圍覆蓋實驗臺的工作平面.最后將測量的磁場數據與背景磁場相減，即可得到由磁源單獨產生的磁場強度.這樣就獲得了磁源對應坐標下的空間磁場數據.通過BP神經網絡對磁場數據和磁源坐標之間的函數進行逼近運算，直到獲得兩者間的映射關系，然后再利用該關系進行磁源定位.為了確定定位精度，不僅計算神經網絡迭代運算的最小均方誤差，而且計算實際定位誤差.定位時隨機選取20個坐標點，每次定位都以此20個點為定位點，并計算定位的均方誤差.

1.1 封裝磁源

在磁場傳感器采集磁源磁場強度時，為了增強磁源的磁場強度，減少地磁場對其采集數據的干擾.把4個直徑10 cm、厚度2 cm的圓柱形永磁鐵，借助0.5 cm木制隔板，相互吸附為一體，并封裝在3D打印的塑料殼中.至此，磁源工作準備完畢.

1.2 搭建實驗平臺

為減少震動等因素的影響，實驗架搭建在HAP-100型光學氣墊隔振平臺上，該平臺底座及平臺臺面均是由典型的鐵磁質材料制作而成，平臺表面均勻分布有間隔2.5 cm的標準孔，作為坐標點.磁源移動范圍為90 cm×120 cm，傳感器采集平面距離實驗臺140 cm，傳感器布局在212 cm×120 cm矩形的4個角上.實驗中使用的磁場傳感器型號為JY61P-RM3100，該傳感器的分辨率為15 nT.1、2、3、4號傳感器分別對應串口號com4、com7、com5、com8，如圖1所示.

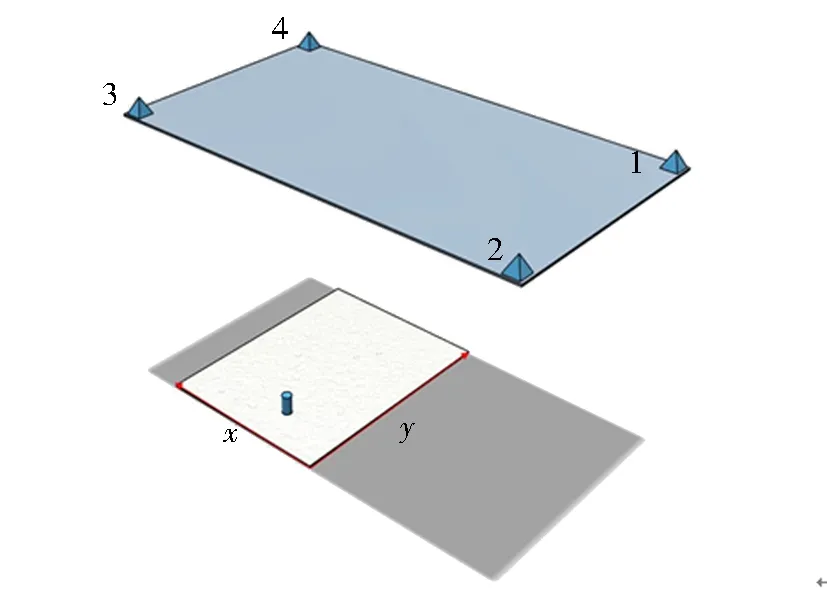
圖1 實驗模型示意Fig.1 Schematic diagram of the experimental model

1.3 構造BP神經網絡

BP神經網絡是一種按誤差反向傳播的多層前饋網絡，具有良好的非線性擬合能力.神經網絡算法通過信息數據正向傳播和誤差負反饋調節的學習機理，多次迭代，實現對輸入輸出數據之間的非線性映射.

BP神經網絡結構如圖2所示.P1，P2，…，P12代表輸入層12個節點的輸入，Wij代表輸入層與隱含層節點之間的權重，f(s1)，f(s2)，…，f(s12)代表隱含層的激勵函數，Wjk代表隱含層與輸出層節點間的權重，x、y代表輸出層2個節點的輸出.

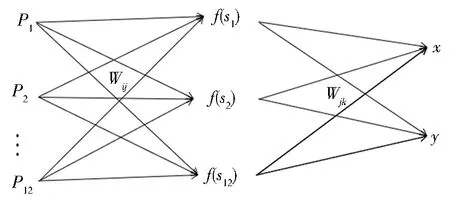
圖2 BP神經網絡結構Fig.2 BP neural network structure diagram

為保證神經網絡磁場定位的精度,以控制變量的思路進行研究.實驗數據處理時采用相同結構的神經網絡.輸入層和輸出層節點由磁場傳感器的輸入維度和輸出維度決定，比如使用4個傳感器采集數據，要獲得磁源在實驗臺上的二維坐標，那么輸入節點12個，輸出節點2個.目前隱層節點數量采用的是試湊法，且設置多少隱層節點與訓練樣本的數量及樣本中復雜關系相關.激活函數，最常用的是f(s)=logsig(s)和f(s)=tansig(s)函數.通過實驗，發現當激活函數為f(s)=logsig(s)時，最優節點在10～12個，如圖3所示.當激活函數為f(s)=tansig(s)時，最優節點為12和14個，如圖4所示.綜合考慮以上2種情況，最終以12為隱層節點數.

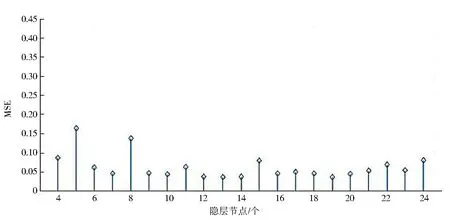
圖3 通過f(s)=log sig(s)得出的MSE Fig.3 MSE from f(s)=log sig(s)

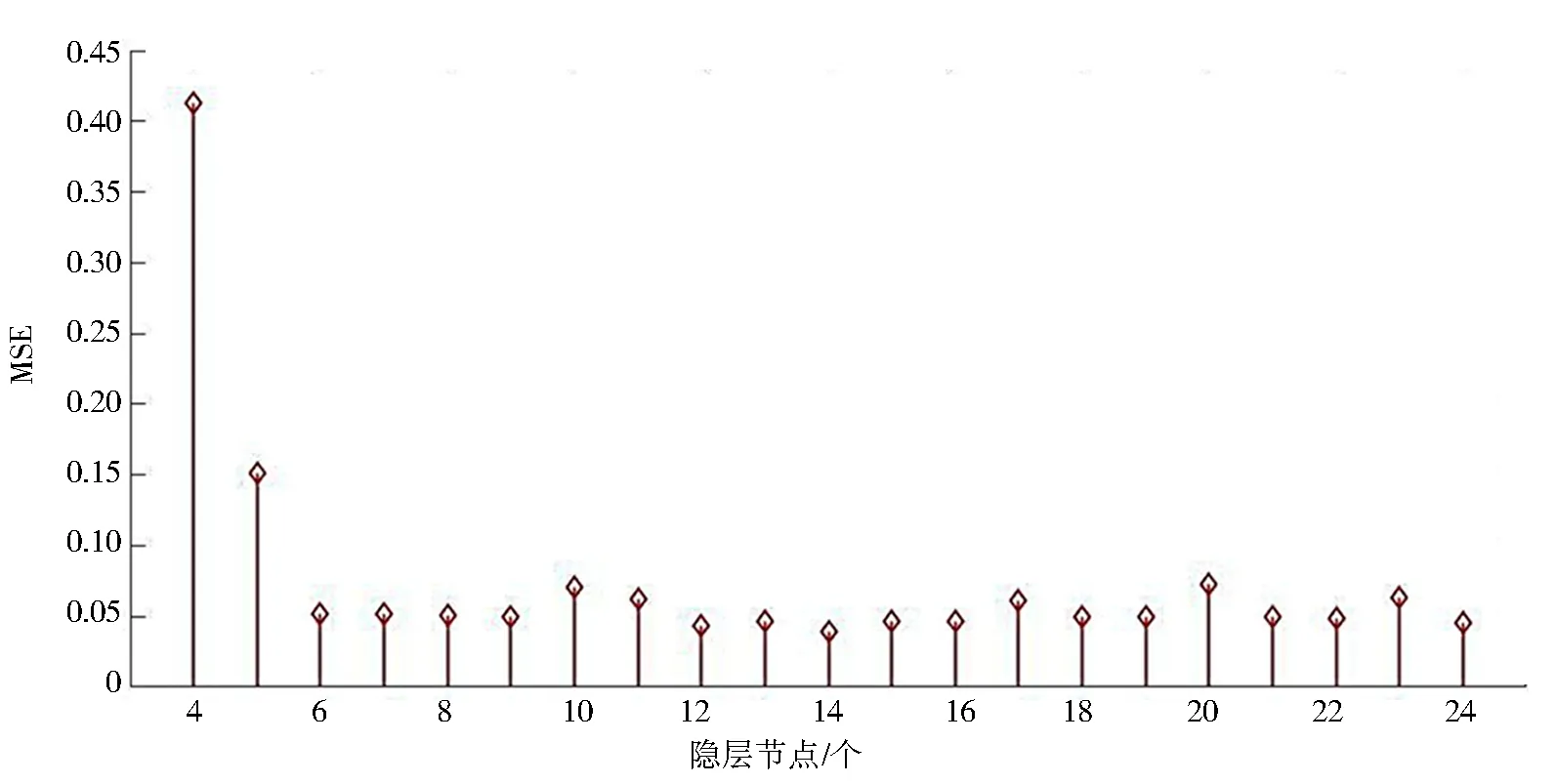
圖4 通過f(s)=tan sig(s)得出的MSE Fig.4 MSE from f(s)=tan sig(s)

基于激活函數f(s)=logsig(s)建立的神經網絡模型在不同隱層節點下更穩定，因此激活函數選取f(s)=logsig(s).

神經網絡算法采用Levenberg-Marquardt算法，該算法在一定程度上克服了基本的BP網絡收斂速度慢和容易陷入局部最小點等問題[22].其他參量設置[23]：學習率為0.01，附加動量因子為0.9，最大確認失敗次數為20，最小性能梯度1×10-5，訓練1 000次，每訓練25次顯示1次[24].

1.4 對比實驗

數據采集量與磁源每次移動步長直接相關，為此進行了3組實驗，每次實驗中僅有步長不同.在實驗1、2、3中，磁源移動步長分別為5.0、7.5、10.0 cm.在傳感器布局與數量驗證實驗中，關閉4號傳感器，以步長7.5 cm進行實驗4；關閉1號、3號傳感器，使用2號、4號傳感器以步長7.5 cm進行實驗5.如表1所示.

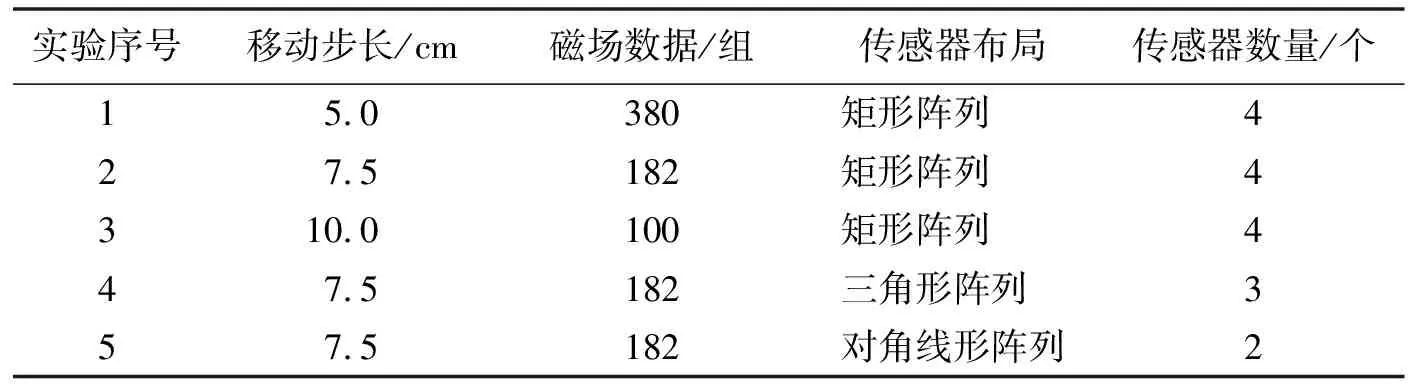
表1 不同實驗對照

實際定位時隨機選取20個坐標點：(0, 0)、(30, 30)、(20, 40)、(50, 20)、(70, 10)、(90, 20)、(60, 30)、(30, 40)、(10, 20)、(80, 40)、(50, 90)、(30, 80)、(60, 70)、(20, 60)、(80, 50)、(90, 90)、(90, 60)、(0, 30)、(10, 80)、(50, 50).

2 實驗結果及分析

2.1 訓練數據的采集

以固定步長移動磁源，通過磁場傳感器記錄磁源運動時對應的空間磁場信息并采集磁源產生的磁場數據.磁源的運動軌跡為首尾相連的“一條龍”形，觀察磁場在磁源周期運動下的變化.實驗中的磁源運動軌跡和對應磁場強度變化情況分別如圖5和圖6所示.由圖6可知，磁源做周期性運動，各個磁場傳感器采集的磁場數據也做周期性變化.

圖5 磁源運動軌跡Fig.5 Motion trajectory diagram of magnetic source

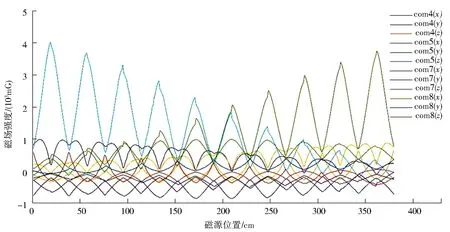
圖6 磁場隨磁源運動變化(380組磁場數據)Fig.6 Changes of magnetic field with the movement of magnetic source (380 sets of magnetic field data)

2.2 定位結果及誤差分析

保存好訓練完畢的神經網絡，然后把磁源坐標輸給神經網絡模擬定位.“*”代表磁源實際坐標，“o”代表神經網絡根據輸入磁場計算的定位坐標，結果如圖7所示，可以看出神經網絡定位坐標非常準確.與此同時，進行了20個隨機坐標點的實際定位，結果如圖8所示，這種情況下的MSE=2.797 1.顯見，實際定位的精度不如神經網絡模擬定位的精度高，這說明輸入神經網絡的磁場數據發生了變化.而磁源的磁場在短時間內無特殊原因并不會退磁.因此，推測誤差變大是由傳感器本身的電子噪聲影響了磁場數據采集造成的.

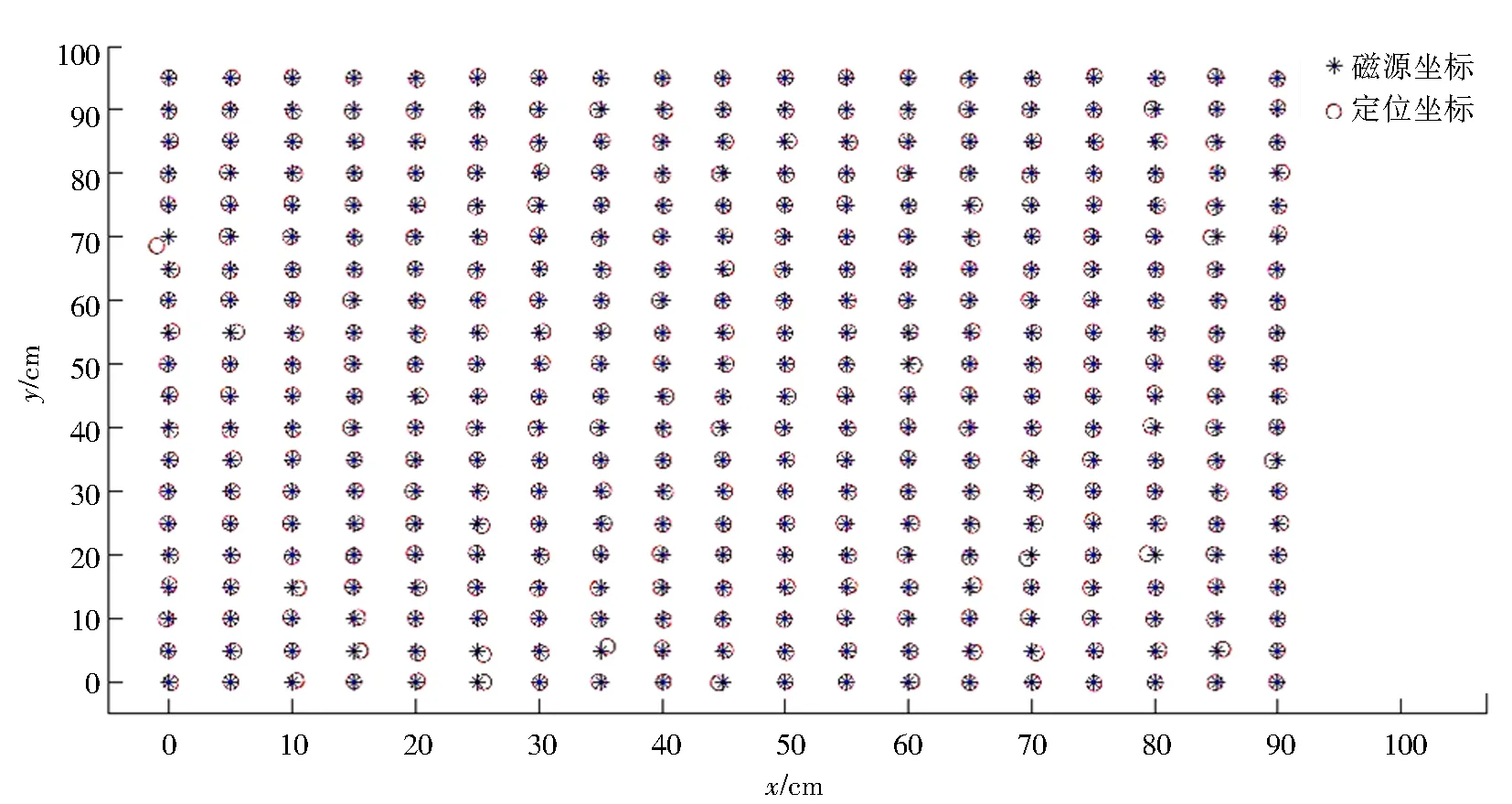
圖7 磁源坐標與BP神經網絡計算坐標對比Fig.7 Comparison of magnetic source coordinates and coordinates calculated by BP neural network

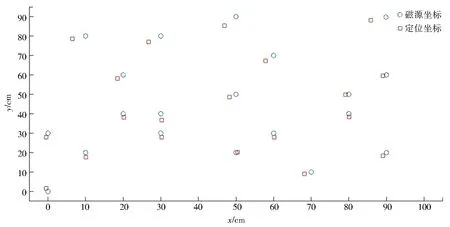
圖8 實際隨機20個點磁源坐標與定位坐標對比Fig.8 Comparison of the magnetic source coordinates and the positioning coordinates of the actual random 20 points

為了驗證上文傳感器電子噪聲的假設，對該20個點的磁場數據加上均值為0、標準差為2.5且服從正態分布的隨機數，再將磁場數據輸入神經網絡進行定位，并與不加電子噪聲的模擬定位進行對比.實驗結果如圖9和圖10所示.比較圖8與圖10，顯見，無論在x方向還是y方向，加入隨機數前的定位坐標均比磁源實際位置坐標偏小；而加入隨機數后的定位坐標與磁源實際位置坐標相比，偏大和偏小的都有，且只有個別點的定位坐標有較大誤差.再次計算加入隨機數后定位結果的MSE，得出均方誤差為2.635 6，與實際定位MSE很接近.因此傳感器電子噪聲影響定位精度的假設基本成立，且該電子噪聲符合均值為0、標準差在2.5～2.6服從正態分布的隨機數.

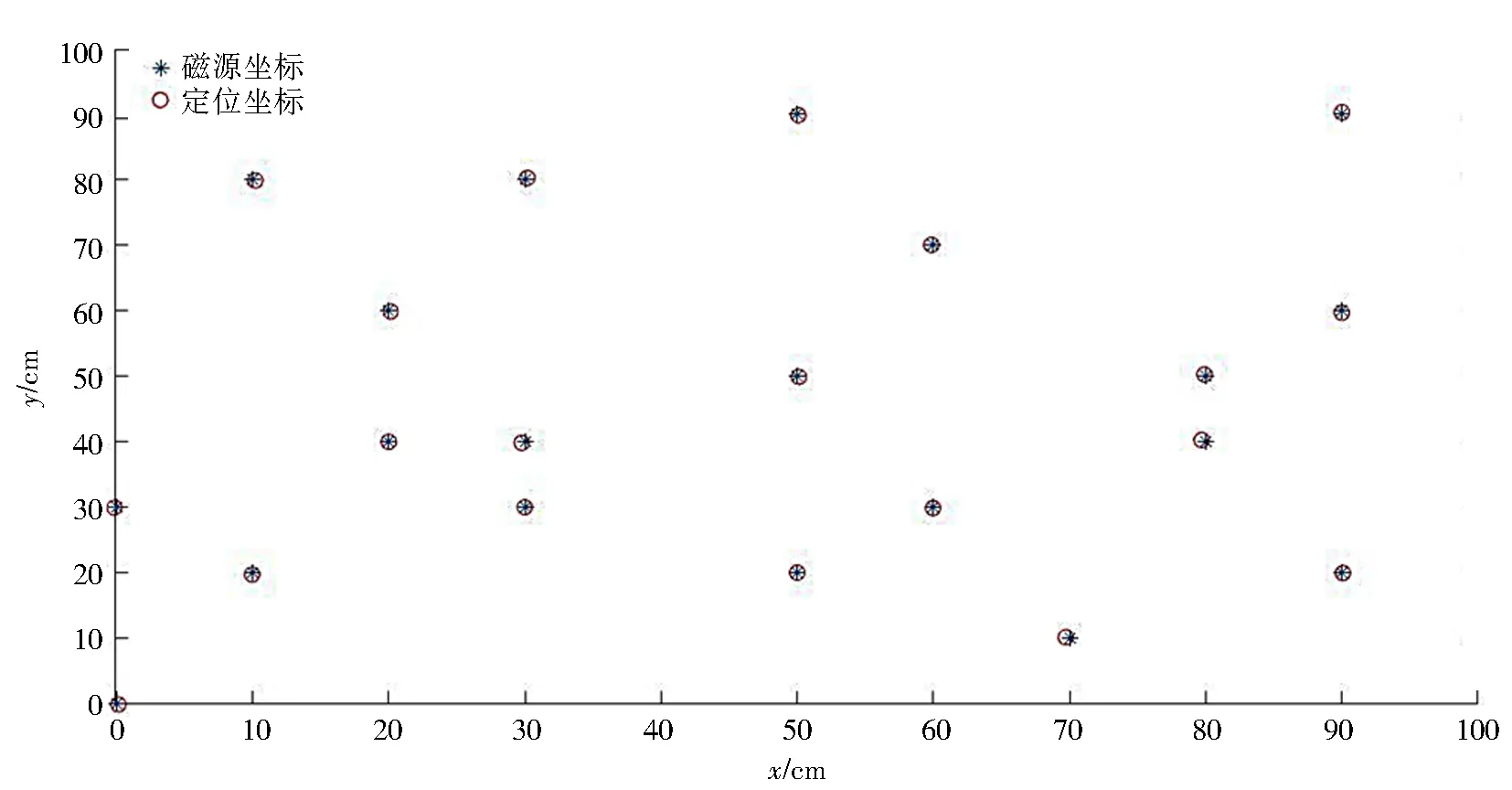
圖9 實際測試點模擬定位Fig.9 Simulated positioning diagram of actual test points

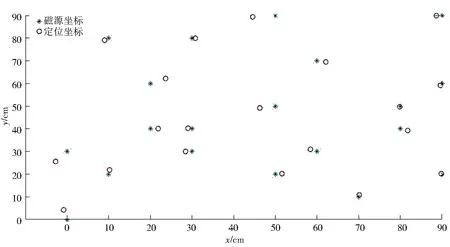
圖10 計入隨機數的模擬定位Fig.10 Simulated location map with random numbers included

按相同的實驗步驟和數據處理方式，進行其他實驗， 得出數據匯總表，如表2所示.

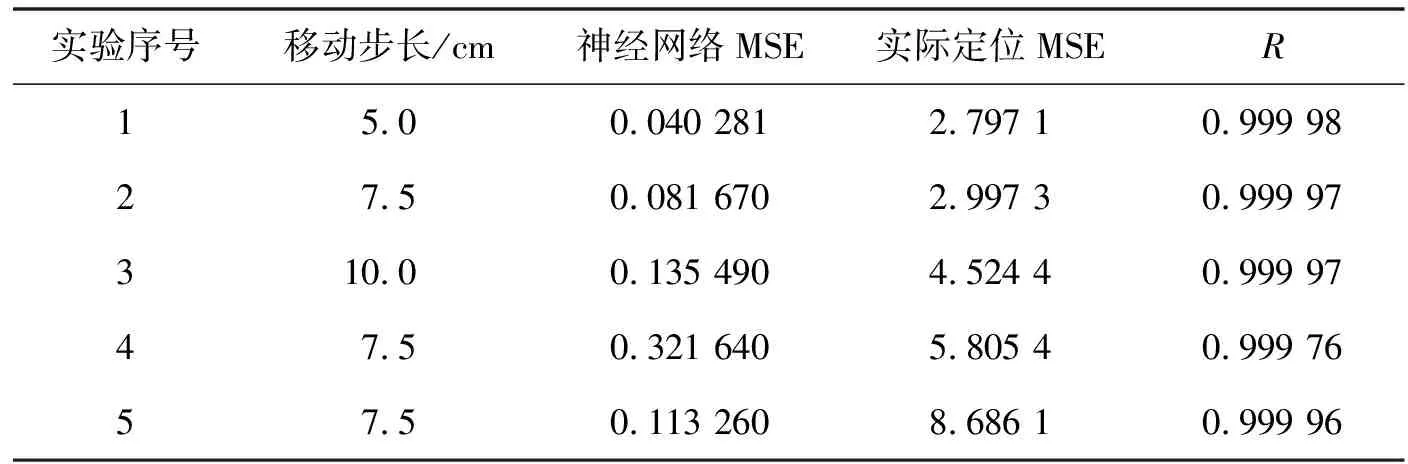
表2 數據匯總

由表2可見，隨著移動步長的減小，神經網絡訓練誤差和實際定位誤差都快速減小，說明增大訓練數據量有益于神經網絡訓練且可以提高定位精度.對于傳感器布局的實驗，以步長7.5 cm，分別進行了矩形、三角形、對角線形布局的實驗.結果表明，矩形布局的實驗效果最好，即傳感器數量越多，定位精度越高.同樣得到采集的數據量越大，定位精度越高.

3 實驗結論

本文中結合BP神經網絡對空間磁介質分布不均勻的復雜環境進行磁場定位，并以實驗采集的360組磁場坐標的對應值為訓練數據，得到了較為準確的定位結果，證明了使用BP神經網絡實現磁場定位的可行性.此外，實驗結果還表明：數據采集時，隨著磁源移動步長的減小，無論是神經網絡的均方誤差，還是實際檢驗的均方誤差，都有所減小；無論傳感器如何布局，傳感器數量越多，定位結果越準確；傳感器電子噪聲對定位結果有一定影響，使用電子噪聲小的傳感器能獲得較準確的測量結果.