基于等幾何分析的三維風力機葉片數值仿真研究

汪 泉， 楊書益， 朱曉霜

（湖北工業大學 機械工程學院， 湖北 武漢 430068）

0 引言

目前，有限元分析是研究風力機葉片空氣動力學性能最常見的計算方法，但在風力機葉片有限元求解中會遇到幾個問題。 一是有限元求解精度與網格的細化程度有關，網格越細，計算結果精度越高，但計算時間和成本也隨之增加。 二是網格劃分工具對風力機葉片等高級復雜曲面識別精度較低，無法精確劃分，會導致計算精度的缺失。三是當風力機葉片模型發生改變，必須重新劃分網格，耗費大量時間。 基于以上原因，Hughes T J R 提出等幾何分析（IGA）的方法，該方法直接結合了CAD 中的幾何模型，將其中的幾何信息作為有限元分析的輸入信息，大大節省了劃分網格的時間[1]。IGA 是基于有限元分析方法的等參單元思想，是將CAD 中用于表達幾何模型的非均勻有理B 樣條的基函數作為形函數，實現了CAD 到CAE的無縫結合。

許多學者對IGA 進行了研究。 陳明飛基于一階剪切變形理論，并采用等幾何有限元方法對任意曲率的功能梯度曲梁進行了自由振動分析[2]。王悅提出了一種基于T 樣條曲面的變網格柔性系統等幾何分析方法，形成了系統的T 樣條單元局部細化算法[3]。 榮吉利研究了IGA 中的HB 樣條基函數構造以及多層貝塞爾提取方法問題， 并通過帶圓孔平板靜力學算例驗證了基于HB 樣條IGA 方法的有效性和準確性[4]。劉宏亮針對結構等幾何優化設計， 系統梳理和綜述了主要的等幾何優化方法及其在結構優化設計中的應用[5]。 Deng X W 將Kirchhoff-Love 殼單元用于3D 葉片建模，在基于Rhino 的Grasshopper 中的集成框架進行建模和分析[6]。 Herrema A J 利用IGA 創建了一個優化設計的框架， 用壓管為例證實了該框架的實用性[7]。 Aung T L 開發了集成IGA 的優化設計框架， 并將其應用于優化兩個焊縫的形狀以減少應力集中[8]。

然而以上研究大多基于簡單模型的IGA，風力機葉片作為一種高級復雜的曲面， 在等幾何方面的應用還很少， 且目前的研究大多是借助三維軟件平臺的二次開發， 沒有實現真正意義上的設計和分析的統一。 為了實現復雜三維風力機葉片設計與分析的完全統一， 避免復雜的網格劃分過程，提高其求解精度與效率，本文開展了風力機葉片的IGA 研究。首先構建適合IGA 的風力機葉片NURBS 模型， 然后推導三維靜力學IGA 相關計算公式，實現三維復雜風力機葉片的IGA。一方面通過簡單算例精確解驗證IGA 算法正確性，另一方面通過與商業軟件對比驗證其優越性。

1 風力機葉片模型的構建

在風力機葉片設計和分析過程中， 設計師通常會先設計其CAD 模型，然后通過有限元分析軟件對其進行網格劃分。 網格劃分的質量決定了仿真分析的精度與效率， 特別對于風力機葉片這種復雜的曲面，容易劃分低質量的網格，從而影響分析結果的精度與效率。 為此本文基于NURBS 構建了適合IGA 的風力機葉片二維三維模型，模型設計和分析均采用同一的基函數， 不僅避免了復雜的網格劃分過程， 同時也消除了模型設計與分析之間的誤差。

1.1 風力機葉片二維翼型的構建

本文將NURBS 作為設計和分析基函數，連接了設計和分析。 一條p 次NURBS 曲線定義為

式中：c（u）為NURBS 樣條函數；pi為控制點；wi為權因子；Ni，p（u）為定義在非均勻節點u 上第i 個P次B 樣條基函數；a，b 為節點矢量u 的取值范圍。

NURBS 曲線具有幾何不變性、凸包性和局部支撐性等性質， 是計算機輔助設計系統中最常見的表示方法。 采用NURBS 構建風力機葉片二維翼型可以提高翼型的光滑連續性，可以更準確、更光滑地構建風力機葉片的翼型，為后續的IGA 提供準確的模型支撐。 利用NURBS 來實現風力機葉片翼型的參數化是翼型設計中至關重要的一步，也是IGA 的基礎。

在Matlab 中， 先編寫翼型反求控制點程序，得到二維翼型的控制點， 然后基于NURBS 理論編寫構建翼型程序，其流程如圖1 所示。

圖1 NURBS 流程圖Fig.1 Flow chart of NURBS

首先選擇翼型的型值點， 然后通過參數化處理確定樣條的階數，求得節點矢量信息，再通過切矢邊界條件，求解線性方程組A*D=E，獲得控制頂點向量D， 接著將得到的控制點和節點矢量及權因子作為輸入參數，得到NURBS 構建的翼型。圖2 為DU97-W-300 翼型分布圖。

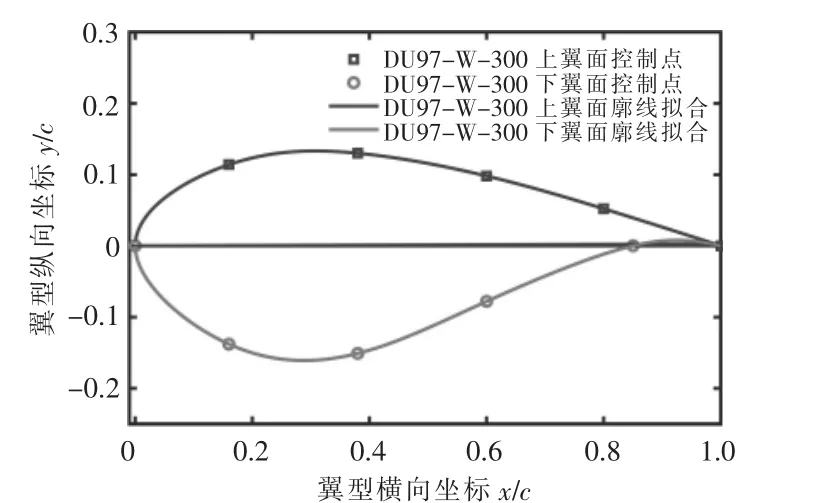
圖2 DU97-W-300 翼型分布圖Fig.2 DU97-W-300 airfoil

選取了部分型值點，求得其控制點為

1.2 風力機葉片三維模型的構建

葉片是以氣動中心軸進行扭轉的， 翼型的氣動中心為1/4 弦長位置， 一般變弦長變扭角的三維葉片集成表達式為

式中：θ 為幅角；u 為葉片展向位置；ρ（θ）為翼型分布函數；a 為擬合系數；xM為翼型氣動中心展向位置，一般取0.25；c（u）為弦長分布函數；β（u）為扭角分布函數。

根據三維葉片的形函數/分布函數公式將其耦合到NURBS 建模中。 分別設置21 個翼型的數據，每個翼型由24 個控制點構成，其中12 個控制上翼型，12 個控制下翼型。

圖3 為基于NURBS 構建的三維風力機葉片模型。模型由21 個翼型組成，每個翼型由24 個控制點組成。

圖3 風力機葉片NURBS 模型Fig.3 NURBS model of wind turbine blade

2 風力機葉片的IGA

2.1 IGA 方法

設定風力機葉片的材料為各向同性材料，風力機葉片的IGA 屬于線彈性問題，風力機葉片在載荷和邊界條件下的位移可以表示為邊界值問題，其位移ui為

式中：Γ 為域邊界；σ 為應力。

式（7）為狄利克雷邊界條件，式（8）為紐曼邊界條件。

IGA 是對上述式進行變分后得到弱形式，對于邊界條件來說，u∈s，v∈V 滿足以下條件：

式中：K 為剛度矩陣；P 為載荷向量。

采用高斯積分方法，在得到了位移值之后，可以求得單元的應變ε 為

式中：L 為微分算子。

由此可得應力σ 為

式中：D 為彈性矩陣，與材料的泊松比和彈性模量有關。

IGA 流程如圖4 所示。

圖4 IGA 流程圖Fig.4 IGA flow chart

2.2 NURBS 算例

為了驗證NURBS 三維實體IGA 的正確性，首先對簡單的算例進行IGA 并與其精確解對比。考慮到受均勻拉力作用下的球形孔洞問題， 算例模型結構尺寸及相關參數如圖5 所示。

圖5 算例模型結構尺寸Fig.5 Model structure size of the calculation example

圖中各參數均為無量綱參數， 其在球坐標系（r，?，θ）的精確解[9]為

式中：a 為球體的半徑；S 為施加的拉力；ν 為泊松比。

由于該算例的對稱性，本文考慮對模型的1/8 進行IGA，并將計算得到的結果與精確解進行對比。 當S=1，ν=0.3 時，σmax=3S（9-5ν）/（14-10ν），其最大應力精確解為2.045 45。 圖6 為球形孔洞的應力云圖。 圖中IGA 計算得到最大應力值為2.05， 而其精確解為2.045 45， 其相對誤差為0.22%。 求解結果與精確解相差無幾，通過此算例驗證了本文構造的IGA 程序的正確性，為后文風力機葉片的IGA 提供了有效的理論依據。

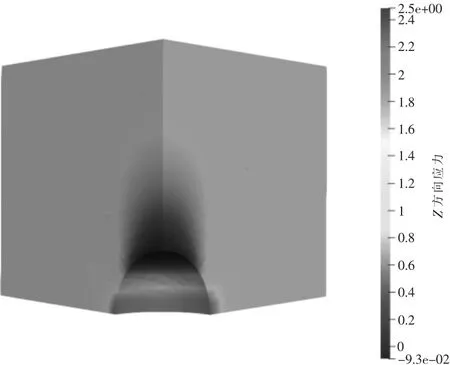
圖6 球形孔洞的應力云圖Fig.6 Stress cloud diagram of spherical holes

2.3 風力機葉片的IGA

在1.2 節中構建了適合IGA 的三維風力機葉片模型，考慮了葉片的彎扭特性，根據文獻[10]，為了方便計算， 將實際風力機葉片模型進行適當簡化，將其材料定義為各向同性材料，材料參數設置為彈性模量為1×105MPa，泊松比為0.3，密度為7.8×103kg/m3。

風力機葉片在正常工作時， 其實際受載情況為揮舞方向、拍打方向和扭矩的耦合。本文考慮在風力機葉片揮舞方向受載這一工況下的三維風力機葉片的等幾何靜力學分析， 根據揮舞方向實際受載情況，其具體約束設置為每個節點的Y，Z 方向固定，X 方向受位移約束-1 mm （圖7 中載荷B），將風力機葉片的葉根位置固定。

圖7 風力機葉片的模型Fig.7 Model of wind turbine blade

將求解結果輸出為.vtu 文件格式， 然后通過將風力機葉片IGA 結果導入開源軟件Paraview中進行可視化，得到了風力機葉片的位移云圖（圖8），在該載荷作用下，其最大位移為2.929 9 mm，最小位移為0.027 5 mm。

圖8 風力機葉片位移云圖Fig.8 Wind turbine blade displacement cloud diagram

3 結果驗證

為了驗證風力機葉片IGA 結果的正確性，將計算所得風力機葉片模型控制點信息通過插入曲線命令導入三維建模軟件SolidWorks 中進行建模，然后將模型導入軟件ANSYS 中構建其有限元模型（圖9）。 將IGA 的結果和與有限元分析的結果進行對比，以驗證風力機葉片IGA 的正確性。

圖9 有限元模型Fig.9 Finite element model

在商業軟件ANSYS 中施加與IGA 相同的材料屬性、 邊界條件和載荷約束， 并進行求解（圖10）。

圖10 有限元結果Fig.10 Finite element results

為了驗證IGA 的正確性，將風力機葉片在相同的條件下進行了有限元分析，葉片在載荷的作用下最大位移為3.012 4 mm，最小位移為0.028 7 mm，IGA 與有限元分析的最大誤差為5.1%。 為了進一步驗證IGA 的正確性，分別取固定位置處的節點，分析對比IGA 和有限元分析的結果（表1）。從不同位置節點位移的對比結果可以看出，IGA與有限元分析的結果誤差均在5.1%以內，進一步驗證了IGA 的準確性。

表1 載荷下的位移Table 1 Displacement under load mm

為了驗證IGA 的優越性，將不同的控制點數目情況下IGA 的結果與ANSYS 結果進行了對比（圖11）。

圖11 兩種方法不同節點數目的位移值對比Fig.11 Comparison of displacement values of the two methods with different numbers of nodes

當節點數為600 時，IGA 的計算結果為2.8831，計算時間為42 s； 當ANSYS 節點數量為2 300時，計算時間為151 s，其計算結果與IGA 計算結果基本一致。 這也證明了在不損失計算結果精度的條件下，IGA 方法較有限元方法節省了大量的節點，提高了求解的效率。

4 結論

本文針對復雜三維風力機葉片， 首先構建了適合IGA 的風力機葉片NURBS 模型， 然后推導三維靜力學IGA 相關計算公式，并編寫了相關程序，實現了三維復雜風力機葉片的IGA。并通過簡單算例精確解和商業軟件對其進行驗證， 得到以下結論。

①構建IGA 框架， 并編寫相關計算程序，通過簡單算例的精確解驗證了其正確性。

②將風力機葉片變弦長變扭角公式與NURBS 相耦合， 構建了適合IGA 的三維風力機葉片模型， 并對構建的模型進行IGA， 并將IGA結果與商業軟件進行對比。對比結果表明：位移最大誤差為5.1%， 驗證了風力機葉片IGA 的正確性； 對兩種方法在不同節點數情況下的計算結果進行對比，在不損失求解精度的情況下，IGA 較有限元分析節省了大量的節點，提高了求解的效率。