基于控制參數分群的DFIG 并網系統低頻振蕩抑制

李生虎， 張奧博， 顏云松， 韓 偉， 宋 闖

（1.合肥工業大學 電氣與自動化工程學院， 安徽 合肥 230009； 2.南瑞集團有限公司 國網電力科學研究院有限公司， 江蘇 南京 211106； 3.國網河南省電力公司電力科學研究院， 河南 鄭州 450052）

0 引言

隨著大規模風電并網， 風電機組如雙饋感應發電機（Doubly-Fed Induction Generator，DFIG）與同步發電機（Synchronous Generator，SG）間動態交互可能加劇電網振蕩，增加新的振蕩模式[1]～[5]。

低頻振蕩（Low-Frequency Oscillation，LFO）一般指頻率在0.1～2.5 Hz，且阻尼比小于閾值的振蕩模式，特征值分析可以確定電網振蕩特性[6]。 文獻[7]考慮了風電場在運行風速、接入容量以及參與無功調度的不同情況，基于特征值分析了LFO 模態的振蕩特性。文獻[8]從風電輸送距離、聯絡線傳送功率等方面研究了DFIG 并網對振蕩特性的影響。文獻[9]，[10]分別描繪了特征值隨鎖相環、虛擬慣量控制參數變化的軌跡， 分析了系統振蕩的變化。加裝電力系統穩定器（Power System Stabilizer，PSS）、靜止無功發生器等裝置，可以提高電力系統穩定性[11]～[14]。 文獻[15]在DFIG 上安裝功率振蕩阻尼器， 采用時域仿真驗證加裝裝置對系統振蕩的抑制效果。但是大部分控制器結構復雜，引入系統會增加投資和保護的成本。 調節風電系統中的控制參數， 如DFIG 變流器內部的PI 參數[16]，[17]，SG勵磁器參數等[18]，也能抑制系統振蕩。 文獻[19]發現系統振蕩阻尼受DFIG 電流內環控制參數影響較大，控制參數的整定可以抑制振蕩。 基于先進優化算法，處理系統中的控制參數，可用來研究風電系統穩定分析和最優控制。 文獻[20]，[21]采用粒子群算法， 以臨界阻尼比最大化為目標函數，對PSS 的參數進行優化。 但是系統中有多種控制參數， 對全局控制參數優化會增加經濟成本，且部分控制參數對振蕩抑制能力有限，因此需要考慮如何選擇主導參數。

特征值靈敏度可用來評估參數調節對LFO的控制效果[22]～[24]。 文獻[25]，[26]分別計算阻尼比對發電機有功、無功的靈敏度，通過靈敏度指標確定發電機調度最有效的方式， 調節發電機出力，增強臨界模式的阻尼。文獻[27]推導了特征值對DFIG-PSS 傳遞函數的靈敏度表達， 分析表明，與參數靈敏度相比，傳遞函數靈敏度精度更高。文獻[28]時域仿真結果表明，對基于靈敏度選擇的主導參數優化， 可以更好地抑制系統振蕩。文獻[29]對多臺發電機按有功調制方向進行同調性分群，可采用類似方法根據參數對系統阻尼調節效果進行分群。

本文建立DFIG 并網電力系統小擾動穩定分析模型。 根據模式振蕩頻率和阻尼比，篩選LFO模式。 建立危險模式阻尼比對控制參數靈敏度的解析表達。基于模式危險程度和阻尼比靈敏度，定義累積阻尼比靈敏度， 描述控制參數對多個模式阻尼比的總體調節效果。考慮風速與負荷波動，以場景分布概率作為權系數， 對不同場景的累積阻尼比靈敏度加權累加。 引入模糊C 均值（Fuzzy C-Means，FCM）聚類算法，按調節效果對控制參數進行分群。 最后給出小擾動分析和時域仿真結果， 驗證了所選主導參數對LFO 模式的抑制效果。

1 風電系統小擾動分析模型

1.1 DFIG 與SG 建模

DFIG 由風力機及其傳動軸、感應電機、轉子側變流器（Rotor Side Converter，RSC）、網側變流器（Grid Side Converter，GSC）、直流電容等構成，如圖1 所示。

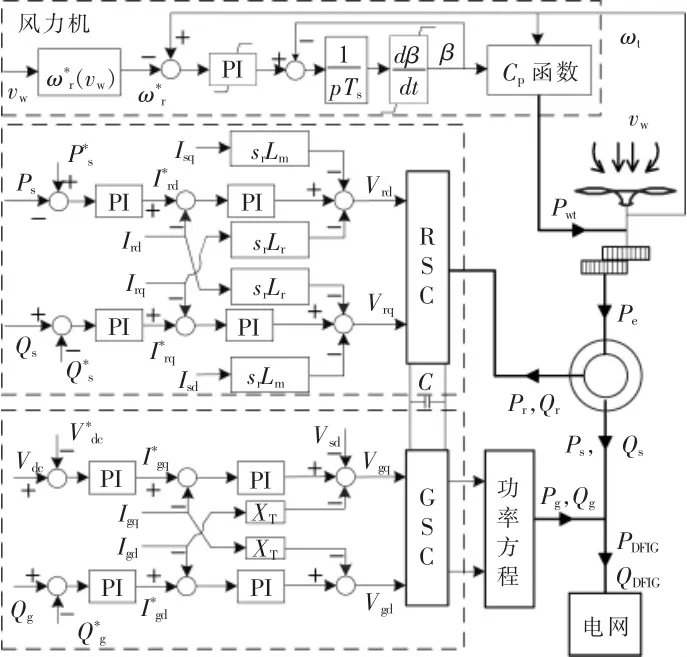
圖1 DFIG 控制模型Fig.1 Control model of DFIG

風力機槳距角控制用于維持風力機轉速和DFIG 有功出力。 RSC，GSC 采用雙環控制。

SG 控制結構如圖2 所示。

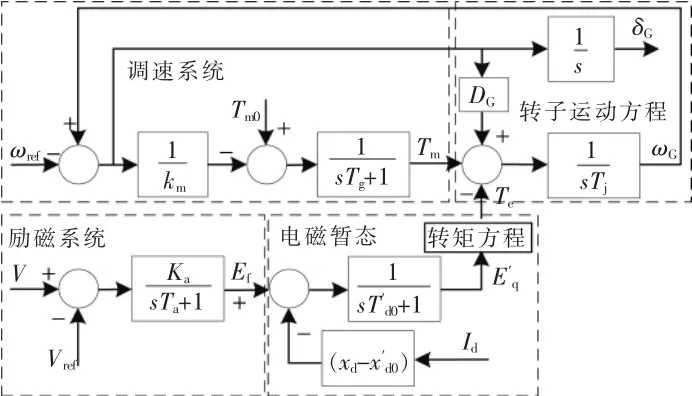
圖2 SG 控制模型Fig.2 Control model of SG

圖中SG 采用5 階動態模型， 包括轉子運動方程（2 階）、轉子電磁暫態（1 階）、勵磁系統（1階）、調速系統（1 階）。

1.2 DFIG 與SG 數學建模

DFIG 并網引入新的狀態變量和代數變量，同時還存在與SG 的動態交互，即：

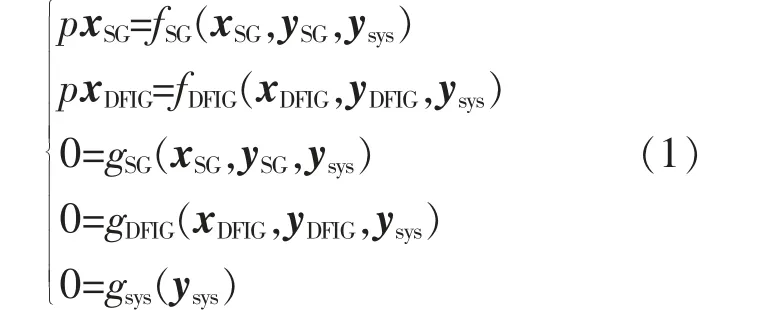
式中：x，y 分別為狀態變量和代數變量的向量形式；fSG，fDFIG分 別 為SG，DFIG 狀 態 方 程 的 函 數 形式；gSG，gDFIG，gsys分別為SG，DFIG，系統代數方程的函數形式；p 為微分算子。

電力系統小干擾穩定分析， 在變量穩定運行點處對系統方程作線性化處理：

式中：Asys為系統狀態矩陣， 可根據Asys計算系統特征值λ、阻尼比ξ 和頻率f，以及用于描述模式與狀態變量相關性的參與因子pkj：

式中：pkj為第k 個狀態變量對第j 個模式的參與因子；Ψ，Φ 為左、右特征向量矩陣。基于阻尼比和靈敏度可用來篩選LFO 模式。

2 累積阻尼比靈敏度和FCM 聚類

2.1 靈敏度模型

風電系統的控制參數， 包括PI 參數、SG 調速、勵磁環節參數等。特征值靈敏度表征控制參數α 的改變對特征值的影響， 其中控制參數α 包括如DFIG 變流器的PI 參數、SG 調速、 勵磁系統的參數等，其解析式為

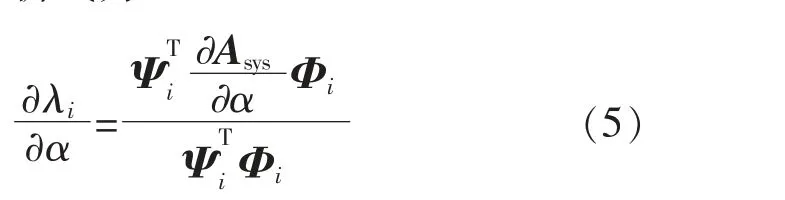
若提高LFO 模式的阻尼比，須進一步推導阻尼比對控制參數靈敏度的解析，其表達式為

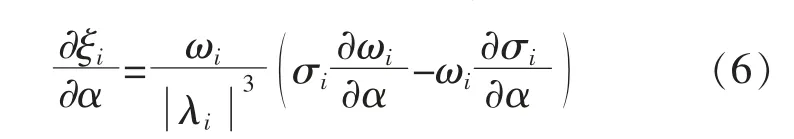
式中：ξi為特征值λi的阻尼比；σi，ωi分別為特征值的實部和虛部。

阻尼比靈敏度量化了控制參數對模式阻尼比的調節效果。 對于有不同的取值范圍和物理意義的控制參數， 評價調節效果應該基于參數的相對調節范圍，而不是絕對調節量。為了消除不同控制參數取值范圍與量綱的差異， 引入相對阻尼比靈敏度用于選擇主導參數[17]，即：

選擇靈敏度數值最大的控制參數作為主導控制參數， 這樣能夠實現相同參數調節量對阻尼比的調節效果最好。 風電系統中有多種LFO 模式，調整控制參數很難實現對所有模式的同向調節，可能出現部分LFO 模式被抑制，而部分模式被惡化的情況。 LFO 模式的阻尼比越小，危險程度越高，這類模式應當被優先調節。可根據阻尼比與設定安全裕度ξcr的相對距離， 定義模式的危險程度。 第i 個LFO 弱阻尼模式的危險系數di為

為了描述控制參數對風電系統中LFO 模式阻尼比的總體調節效果，定義控制參數αj的累積阻尼比靈敏度Sj，其表達式為

式中：X 為LFO 模式的集合。

累積阻尼比靈敏度Sj考慮不同LFO 模式的危險程度，將阻尼比靈敏度加權累加，反映了控制參數變化時，LFO 模式阻尼比的總體變化趨勢。采用模式的危險程度作為權系數， 使得阻尼比小的模式被優先調節。Sj的數值越大，表明參數對模式阻尼比的總體調節效果越好。 當參數對不同模式有相反的調節效果時， 阻尼比靈敏度的累加會相互抵消。 基于Sj篩選得到主導控制參數，通過犧牲一些危險程度低的模式，而實現LFO 模式阻尼比的總體提升。

風電系統中， 風速和負荷的波動通過影響潮流的分布，改變小干擾穩定分析計算的結果，進而改變振蕩模式的分布。不同的風電場景，LFO 模式集合X 可能不同，分布概率也有差異。 基于Sj選擇控制參數，可能無法適應于多個場景。因此需要劃分風電場景， 保證同一場景的樣本有相近的特征，而不同場景都有各自明確的特征。基于歷史實測風電場數據，采用聚類算法，將具有相近特性的樣本數據聚成一類，得到各個不同的風電場景。聚類中心點代表了各類的平均水平， 避免了考慮風速時刻波動的復雜運算。

本文采用FCM 聚類算法處理風速和負荷數據。為了確定適用于多個風電場景的主導參數，引入不同風電場景的概率密度作權系數， 將聚類中心作為典型風電場景， 計算每一類風電場景的LFO 模式集合， 對累積阻尼比靈敏度進行改造，即：

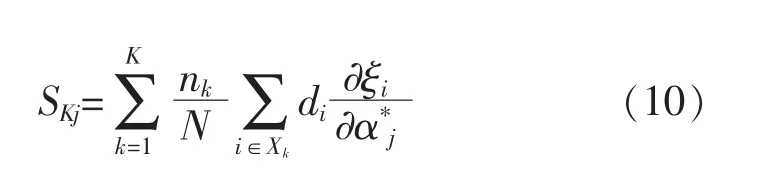
式中：nk為第k 類場景的樣本數；K 為風電場景聚類數；N 為總樣本數；Xk為第k 類場景的LFO 模式集合。

SKj考慮了不同風電場景、 振蕩模式的變化，使控制參數對阻尼比的調節， 可能出現某些概率小的場景效果好，概率大的場景效果差的情況，還可能出現不同場景調節效果相反。 本文選擇的主導參數要能夠適用于更多場景， 因此將場景的概率分布設為權系數，使得在分布概率大的場景中，調節效果好的控制參數的作用更加明顯。

在風電系統多個控制參數中， 確定主導控制參數，難點不僅在于推導靈敏度的解析表達，還在于高效選擇控制參數。對于主導控制參數，靈敏度數值特征明顯高于其他參數。 采用FCM 聚類算法， 基于累積阻尼比靈敏度， 對控制參數進行分群。累積阻尼比靈敏度數值大小，用來劃分主導參數，符號用來判斷調整方向。 聚類后，同一聚簇的控制參數對阻尼比有相同調整方向、 相近調節效果，通過比較不同聚簇便可確定主導參數組。只需從聚類結果中挑選出兩類聚簇， 即上調主導參數簇Ωup和下調主導參數簇Ωdown， 而無需再將控制參數的靈敏度結果依次進行比較。

2.2 FCM 聚類算法

FCM 算法是基于二次目標函數最小化的迭代優化算法， 數據的隸屬度基于數據距聚類中心的距離決定。 本文提供了一種用于抑制風電系統LFO 模式主導參數分群方案。 首先根據風電系統小干擾穩定分析結果，篩選LFO 模式，推導阻尼比對控制參數靈敏度的解析表達，計及模式危險程度，計算累積阻尼比靈敏度，同時引入不同風電場景的分布概率，采用FCM 算法對控制參數進行分群，得到對多模式、多場景有較好調節效果的主導參數組，具體流程如圖3 所示。 本文所提算法不限于對DFIG 并網系統， 也不限于調節LFO 模式阻尼比，可用于同步發電機、改善其他振蕩模式或評估指標。

圖3 抑制LFO 控制參數分群流程Fig.3 Flow chart of parameters clustering to damp LFO

3 算例分析

本文采用新英格蘭39 節點測試系統， 如圖4所示。

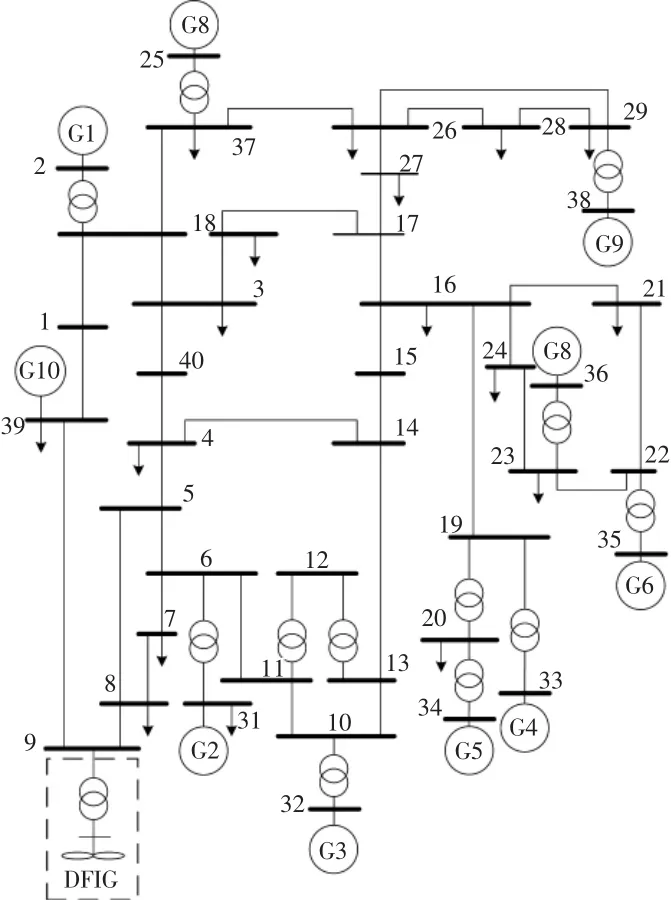
圖4 新英格蘭39 節點測試系統Fig.4 New England 39 node test system

風電機組經變壓器并入9 號節點。 SG 控制參數如表1 所示。 DFIG 結構參數見文獻[30]，[31]，PI參數如表2 所示。 基準功率為100 MV·A，初始風速為12 m/s。 阻尼比安全裕度ξcr設定為0.1[32]，[33]。

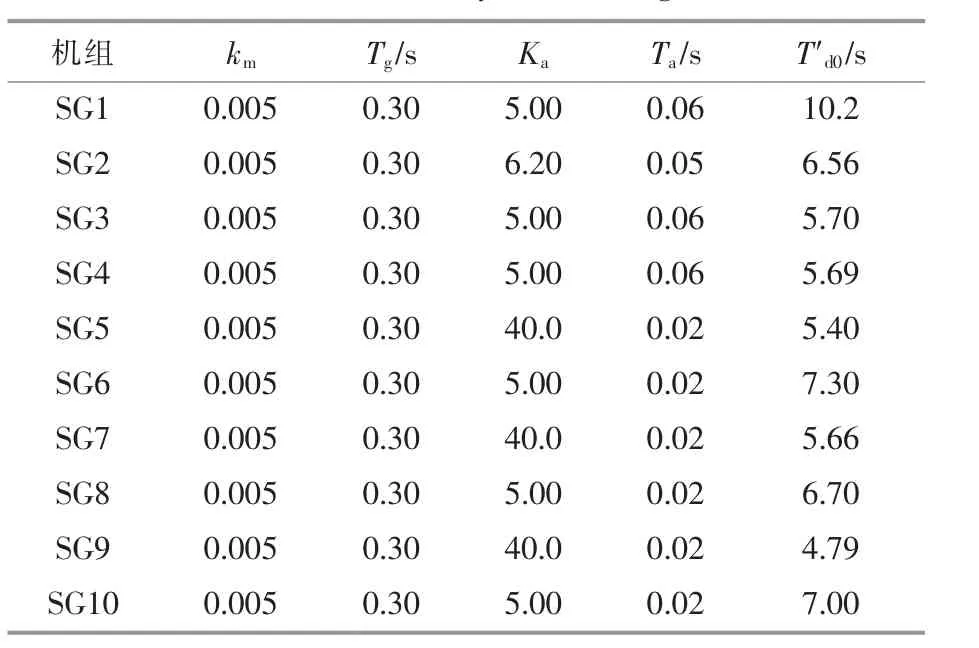
表1 同步發電機參數Table 1 Parameters of synchronous generators

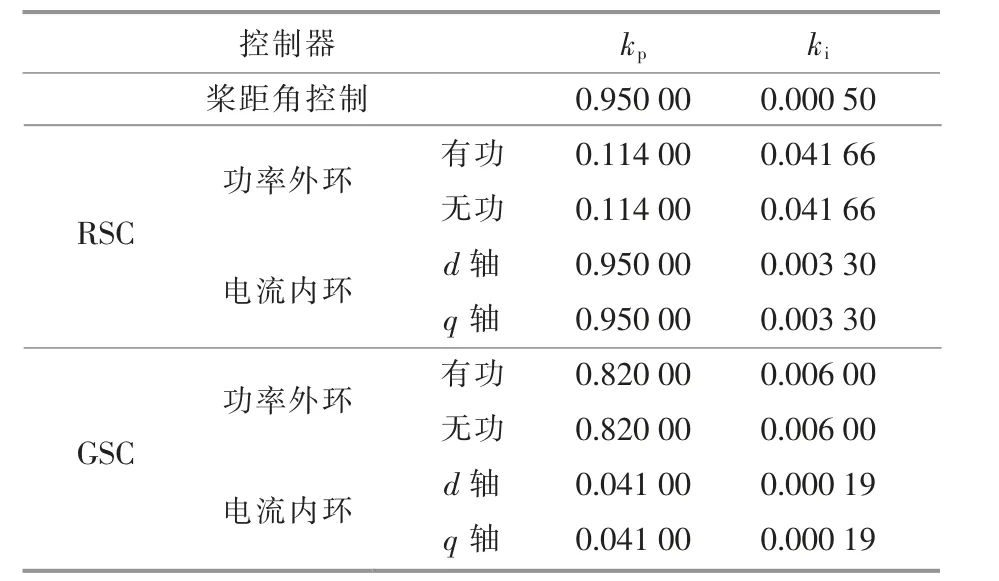
表2 PI 控制器參數Table 2 Parameters of PI controller

3.1 DFIG 并網對LFO 模式的影響

分別對DFIG 并網前后的測試系統進行小干擾穩定性分析，計算特征值、頻率、阻尼比，結果如表3 所示。

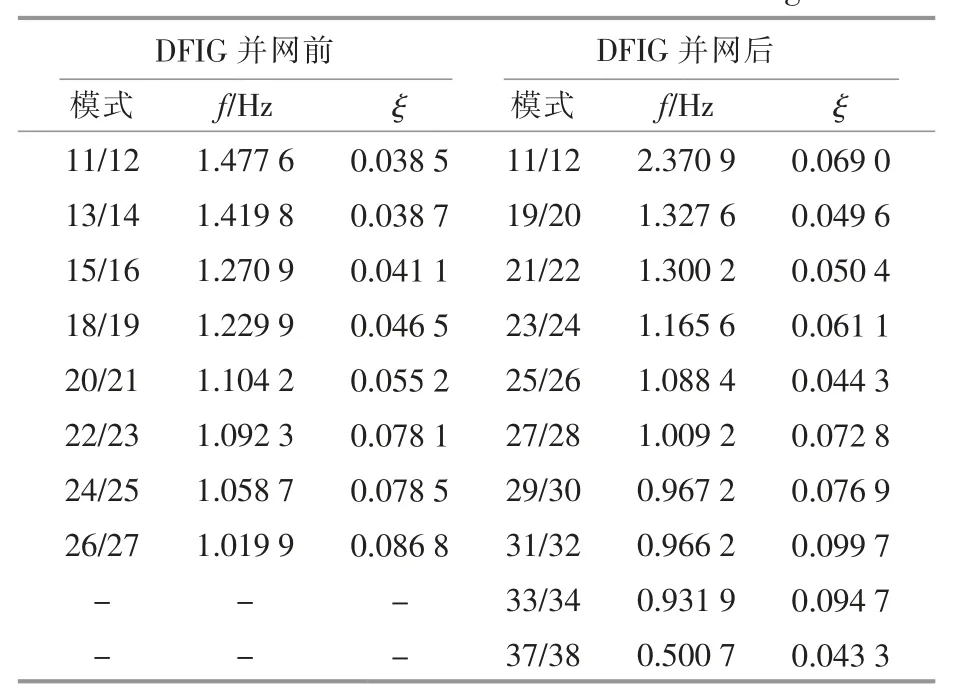
表3 DFIG 并網前、后LFO 模式Table 3 LFO modes before and after DFIG integrated

DFIG 并網前， 系統有8 個LFO 模式，DFIG并網后增加了新的LFO 模式。 由參與因子計算結果， 模式11/12，37/38 與DFIG 狀態變量相關，屬于DFIG 引入模式。 其中模式19/20，25/26，37/38的阻尼比小于0.05，屬于LFO 弱阻尼模式，屬于危險程度高的模式，需要重點關注。

3.2 基于累積阻尼比靈敏度的參數分群

表4 列出了部分LFO 模式阻尼比對控制參數的相對靈敏度計算結果。 對于DFIG 引入的LFO 模式，PI 參數調節效果要明顯好于SG 的控制參數，而對于SG 相關模式，PI 參數并未有明顯的調節效果，Tg的調節效果明顯更優。 對于部分控制參數如ki2，根據阻尼比靈敏度結果，對模式11/12，37/38 的阻尼比都有較好的調節效果，但是調節方向相反。 在計算累積阻尼比靈敏度的過程中，兩種相反的靈敏度數值相加，最終Sj的結果很小，因此不會將這類參數分群到主導參數組中。

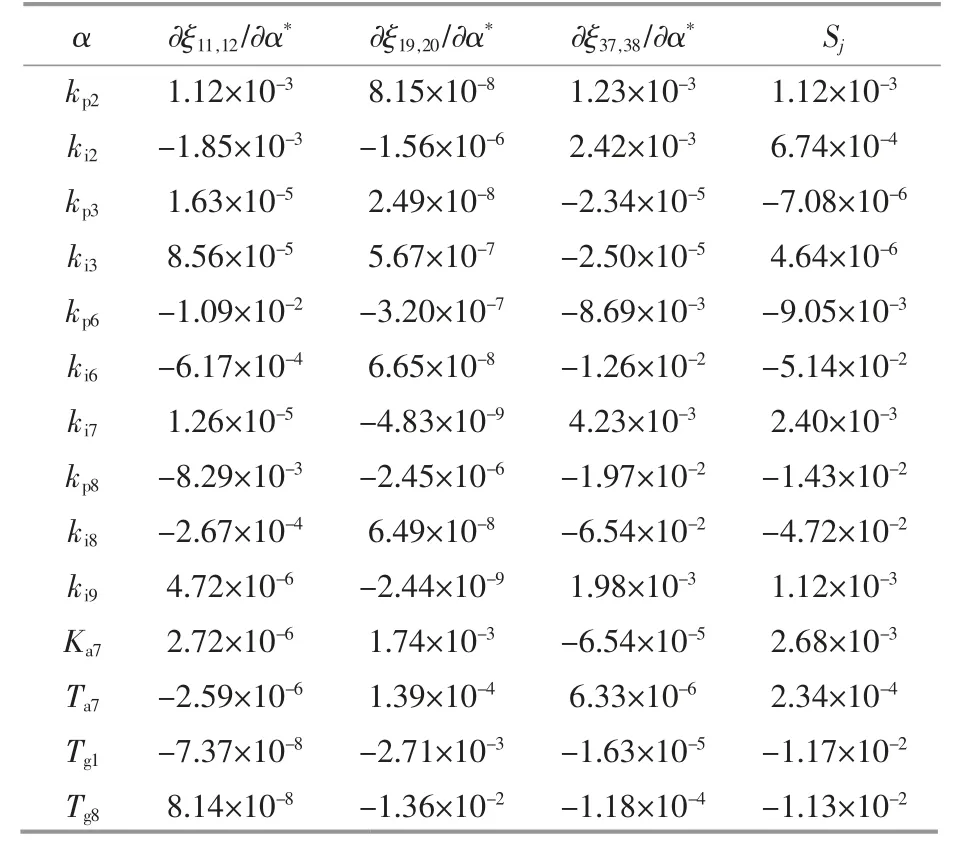
表4 阻尼比對控制參數的相對靈敏度Table 4 Relative sensitivity of damping ratio to control parameters

為驗證本文所提出方法的正確性， 采用攝動法與解析法所得的靈敏度模型進行比較，以ξ25，26，ξ37，38為例，結果如圖5 所示。兩條曲線在初始運行點相切，驗證了阻尼比靈敏度解析表達的正確性，可用于描述控制參數對阻尼比的調節效果。

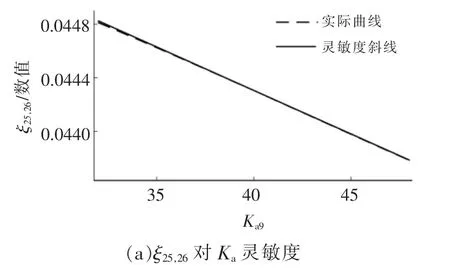
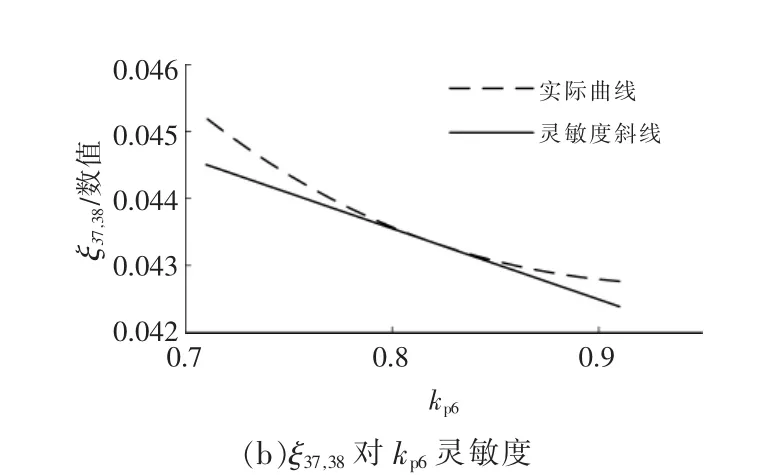
圖5 靈敏度模型驗證Fig.5 Validation of sensitivity model

對于DFIG 和SG 相關LFO 模式的調節，可以對PI 參數與SG 控制參數分別進行處理。 基于FCM 聚類算法對控制參數分群，選擇出對LFO 調節效果最好的參數聚簇，即主導參數組，結果如表5 所示。

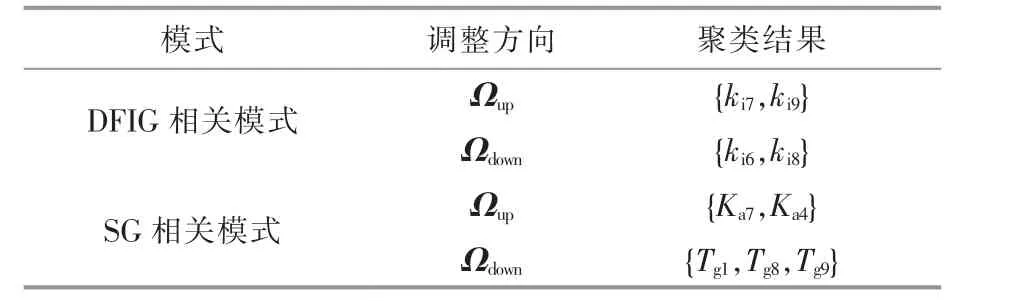
表5 基于FCM 控制參數分群Table 5 Clustering to control parameters based on FCM

為了檢驗本文所提控制參數分群方法， 相較于傳統基于阻尼比靈敏度選擇的控制參數，對LFO 模式有更好的調節效果， 采用時域仿真進行驗證。設定系統7 號節點在0.5 s 時發生三相短路故障，在0.6 s 故障消除，仿真總時間20 s。 選擇19/20，25/26 兩種LFO 弱阻尼模式，由相關因子可知，這兩種模式的強相關變量分別為ω1，ω6。 時域仿真結果如圖6 所示。 通過調節基于靈敏度排序和累積相對靈敏度聚類得到的主導參數， 都能對LFO 有一定抑制作用。 而在保證所調節參數相對調節量相同的條件下， 基于累積阻尼比靈敏度聚類得到的主導參數組， 調節效果優于基于阻尼比靈敏度選擇的參數， 因為基于靈敏度只能選擇對本模式調節效果好的主導參數， 而基于本文方法得到的主導參數群，能夠兼顧更多的LFO 模式。

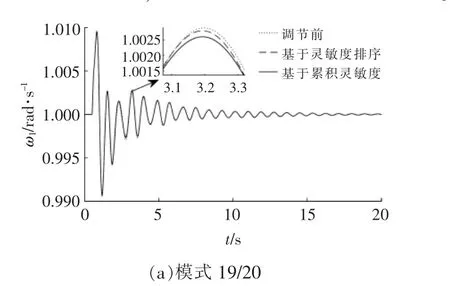
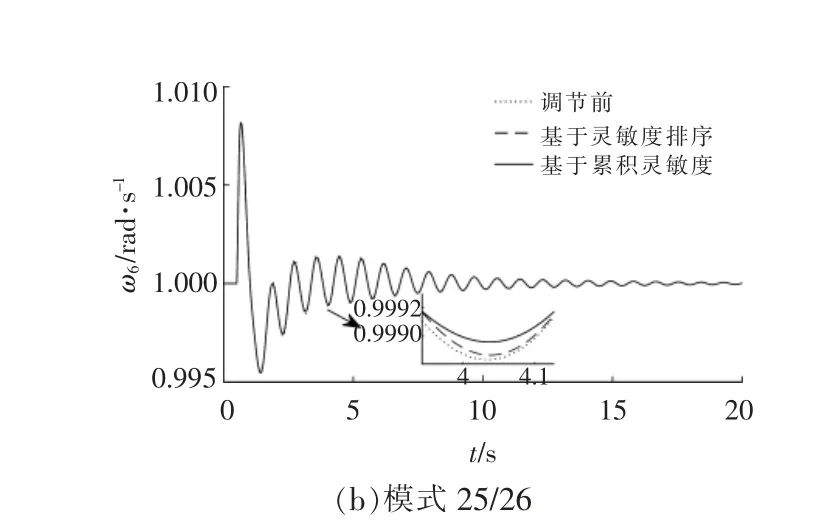
圖6 調節主導參數對LFO 的抑制效果Fig.6 Damping effect of dominate parameters adjustment on LFO

3.3 多風電場景分析

在節點9 的DFIG 接入某地風電場風速數據，在節點1 處加入負荷數據。 基于FCM 聚類算法，將所得到的風速-負荷數據進行聚類，聚類得到各類的中心和樣本數量如表6 所示。

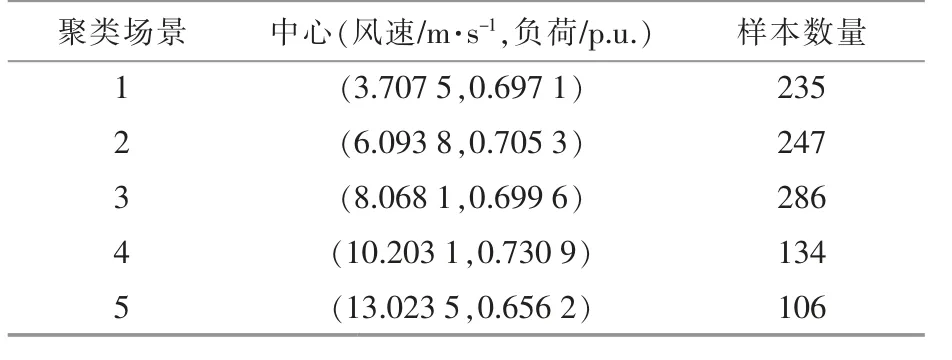
表6 聚類中心和樣本數量Table 6 Clustering center and sample size

由表6 可以看出，聚類分布較為均勻，可用以描述風速的隨機性與波動性數據特征。

將聚類中心作為典型風電場景，帶入特征值，計算每一類場景的累積阻尼比靈敏度， 以及多場景累積阻尼比靈敏度，如圖7 所示。

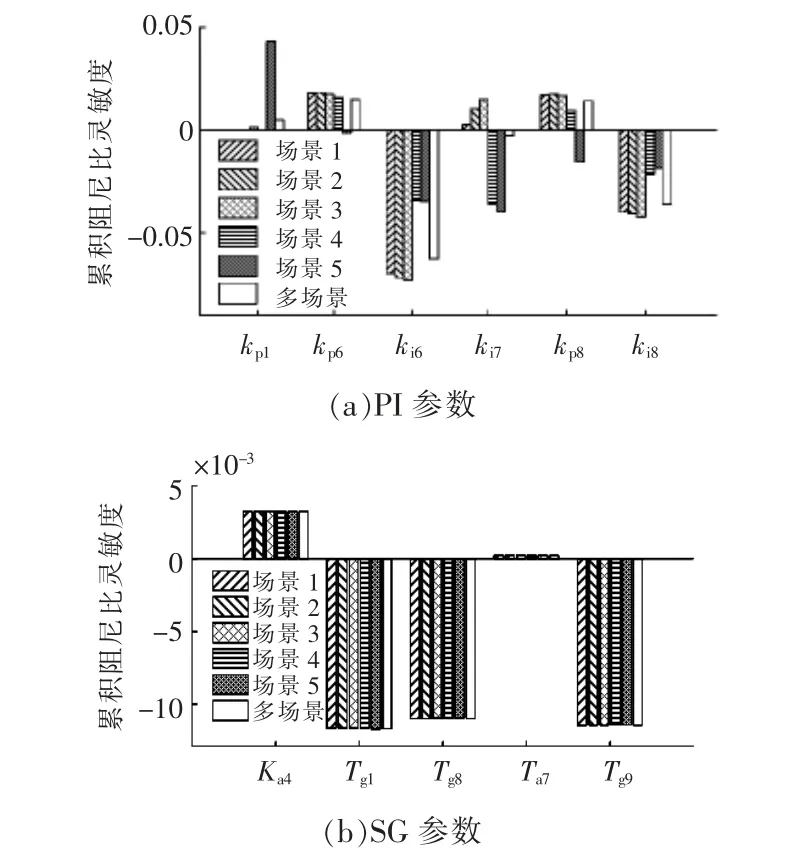
圖7 多場景累積阻尼比靈敏度Fig.7 Multi-scenario cumulative sensitivity of damping ratio

隨著風電場景的改變， 由于風速的改變影響更多的是DFIG 引入的振蕩模式，部分PI 參數的累積阻尼比靈敏度變化較大。如kp1在場景5 累積阻尼比靈敏度數值突然增大，因為該場景下DFIG啟動了槳距角控制， 但是在其他風電場景下對阻尼比提升并無貢獻；ki7在不同場景下對阻尼比的調節方向不同，無法作為多場景下的主導參數。圖7（b）中SG 控制參數在不同風電場景下累積阻尼比靈敏度數值變化不大， 因為靈敏度結果與振蕩模式和系統的拓撲結構有關， 而風電場景的改變對SG 相關振蕩模式影響較小， 系統結構也未發生改變，因此SG 控制參數分群的結果影響不大。對于PI 參數，基于單一場景的累計靈敏度得到的主導參數組可能無法適用于多種場景，需對PI 參數重新分群， 使所選主導參數盡可能的適應不同場景。

基于多場景下累積阻尼比靈敏度，對PI 參數重新進行分群，結果如表7 所示。

表7 適用多場景的PI 參數分群Table 7 Clustering to PI parameters for multiple scenarios

為了驗證所得主導控制參數組能適應多個風電場景，按主導參數組調整方向，對每個參數調節0.1 p.u.。 選取風速數據差距最大的場景1 和場景5，觀察阻尼比的調節效果，如表8 所示。

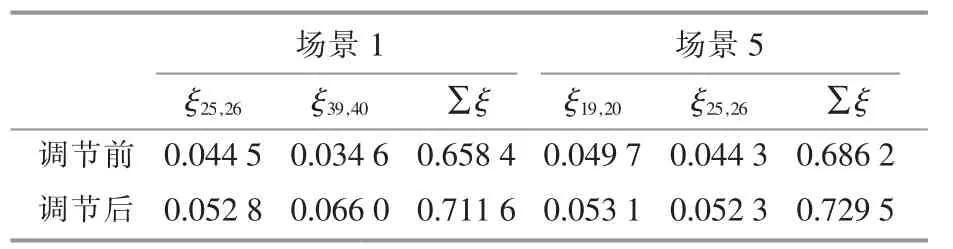
表8 調節主導參數對阻尼比的影響Table 8 Effect of dominate parameters adjustment on damping ratio

在這兩個場景中， 系統阻尼比最小的兩個模式和總阻尼比都是提升的， 雖然沒有完全消除LFO 模式，但是提高了系統的阻尼比，有利于LFO模式的抑制。

4 結論

為改善風電系統小干擾穩定、 抑制LFO 模式，并考慮風速波動對抑制方案的影響，提出了一種基于累積阻尼比靈敏度的控制參數分群方法，得到以下結論： ①基于累積阻尼比靈敏度， 采用FCM 聚類算法對控制參數進行分群，得到控制參數組。時域仿真結果表明，相較于選擇各模式參數靈敏度數值最大的為主導參數， 本文所提方案得到的主導參數組， 對LFO 抑制效果更加明顯；②多風電場景下， 風速變化影響DFIG 相關振蕩模式， 因此有必要引入風電場景分布概率修改累積阻尼比靈敏度。小干擾分析結果表明，調節控制參數組中主導參數，弱阻尼模式阻尼比和LFO 模式阻尼比之和在不同風電場景中都有所提升。

本文所提算法在雙饋風電機組并網系統得到了應用，對于其他風電機組以及光伏并網系統，本文所提控制參數分群算法對低頻振蕩模式的抑制效果，可在后續研究中進一步驗證。