基于Arnold變換的量子圖像混沌加密方法

石金晶 陳 添 陳淑慧* 李 琴 施榮華

①(中南大學計算機學院 長沙 410083)

②(湘潭大學計算機學院 湘潭 411105)

1 引言

圖像傳輸不僅攜有通信者之間的敏感信息，還含有不可估量的樣本數據，如何可靠有效地進行圖像傳輸便成為網絡通信中的重點研究方向之一。基于量子疊加和量子糾纏等特性，很多杰出的量子算法[1–4]被提出，從而威脅到大多基于數論的經典密碼算法的安全性。因此在當今信息飛速發展的時代，設計出更加安全有效的圖像密碼算法至關重要。

早在2013年，Zhou等人[5]結合經典密碼和量子幾何轉換首次提出了量子圖像密碼的概念，為圖像加密提供了新的研究方向。目前為止，關于量子圖像加密算法的研究方式主要分為兩種：一種是基于量子仿射變換和隨機旋轉操作[6–8]來更改圖像的像素位置和像素值以模糊明文圖像；另一種則處于較新的研究領域，即基于混沌系統生成的混沌系數來控制量子邏輯門[9]。雖然后者發展不久，但在密碼研究方面具有潛在的優勢：根據混沌系統生成的混沌系數(隨機數)使每次加密對象的處理參數均不同，從而比固定參數的加密方法更能抵抗重放攻擊。

2013年Yang等人[10]首次將雙重隨機相位編碼技術引入到量子密碼研究當中，并結合量子傅里葉變換提出了量子圖像加密算法。哈密頓量對初始參數的超敏感性可使量子系統呈現出混沌力學行為[11]，2013年Abd等人[12]便利用Goggin等人[13]提出的量子邏輯斯蒂(logistic)映射，設計了一種新的經典彩色圖像加密方案，進一步增加了密鑰空間與算法性能。接下來，為了改進經典圖像加密算法的安全性及圖像處理效率，Tan等人[14]利用陳氏超混沌系統[15]和量子傅里葉變換實現了量子彩色圖像加密算法，該算法計算復雜度為O(n2)，相比于經典圖像加密算法具有指數級優化。2016年Yang等人[16]通過構建1維量子細胞自動機實現了量子圖像加密方案，在安全性和魯棒性方面具有一定優勢。2018年Liu等人[17]基于量子Arnold變換和量子比特隨機旋轉提出了雙重量子圖像加密方案，由量子傅里葉變換實現的量子比特隨機旋轉操作使得其計算復雜度為O(n2)。同年，Zhou等人[9]結合5D超混沌系統和量子交換操作來增強量子彩色圖像加密方案中的隨機性和不可預測性，相比于經典圖像加密方案在有效性和安全性方面具有一定的改善。鑒于當前實際量子資源的稀缺性，為進一步降低計算復雜度，2018年Wang等人[18]使用小波變換存儲圖像的低頻部分來縮小圖像，旨在提高處理圖像效率并降低計算復雜度到O(n)。但是，該方法由于不能完全解密出原始圖像，因此不適用于要求高清晰度解密圖像的場景當中。2019年，Khan等人[19]提出一種基于置換的特殊線性變換應用于量子圖像加密算法，能夠抵御一定程度的密鑰攻擊。2020年，Liu等人[20]基于位平面排列和正弦邏輯映射提出了一種新的量子圖像加密算法，其加密圖像有著更高的信息熵，但難以抵抗高裁剪攻擊的情況。2021年，Liu等人[21]在此基礎上采用Arnold變換和logistic映射進一步優化了加密圖像的信息熵和抗噪聲攻擊性。可見，優化算法的安全性、計算復雜度與解密圖像清晰度等各項評判指標仍是目前量子圖像密碼研究方向的重點。

基于混沌系統的量子圖像加密算法具有密鑰強敏感性和巨大的密鑰空間，能夠抵抗許多非法攻擊[14,22,23]，提高圖像密碼方法的安全性與加解密效率。量子細胞神經網絡作為混沌系統可以實時、并行地對信號進行處理，并被廣泛應用于數據量大的圖像處理當中。此外，相對于傳統的細胞神經網絡，量子細胞神經網絡還具有低消耗、高集成的特點，因而更符合實際應用需求[16,23]。量子酉操作(量子邏輯門)具有可逆性，即在保證量子態不被破壞的情況下，量子邏輯門的輸入、輸出態可以進行相互轉換，可用于提高解密圖像的清晰度。為此，本文結合量子細胞神經網絡和量子酉操作，提出一種新的量子灰度圖像混沌加密方法，在確保量子圖像加密算法安全的基礎上，進一步優化解密圖像清晰度及計算復雜度。此外，本方案中所涉及的圖像處理操作包括量子細胞神經網絡(混沌系統)均可由量子線路實現，表明本方案具有在量子設備上實現的前景。

2 理論基礎

2.1 量子細胞神經網絡的超混沌屬性

混沌是非線性系統中普遍存在的現象。混沌系統[15,24]憑借不確定性、不可重復性和不可預測性被廣泛應用于密碼學中。超混沌系統屬于高維度混沌模型，對于初始控制參數具有超敏感性。由多個量子細胞機構成的量子細胞神經網絡屬于一種超混沌系統[25,26]。具體來講，量子細胞神經網絡的第k個細胞機的動態特性表示為經網絡的混沌屬性，可以令w2為自變量，計算出該量子細胞神經網絡的最大李雅普諾夫指數[28]。如圖2所示，最大李雅普諾夫指數值均大于0，證明耦合2個細胞機的量子細胞神經網絡模型系統便很容易產生超混沌現象。

圖2 量子細胞神經網絡的最大李雅普諾夫指數

2.2 新型量子圖像表示方法

可見，相比于經典圖像表示方法，該量子圖像表示方式能指數級降低圖像存儲空間：對于同一個2n×2n大小的經典灰度圖像，該量子圖像表示方式所需量子比特數為8 +2n，而經典圖像表示方法則需比特數8 ×2n×2n+n2。另外，相比于其他量子圖像表示方法[30,31]，該量子圖像表示方式可以平方級降低制備圖像的時間復雜度，且能夠完全正確地表示出經典圖像[16]，量子線路如圖3所示。

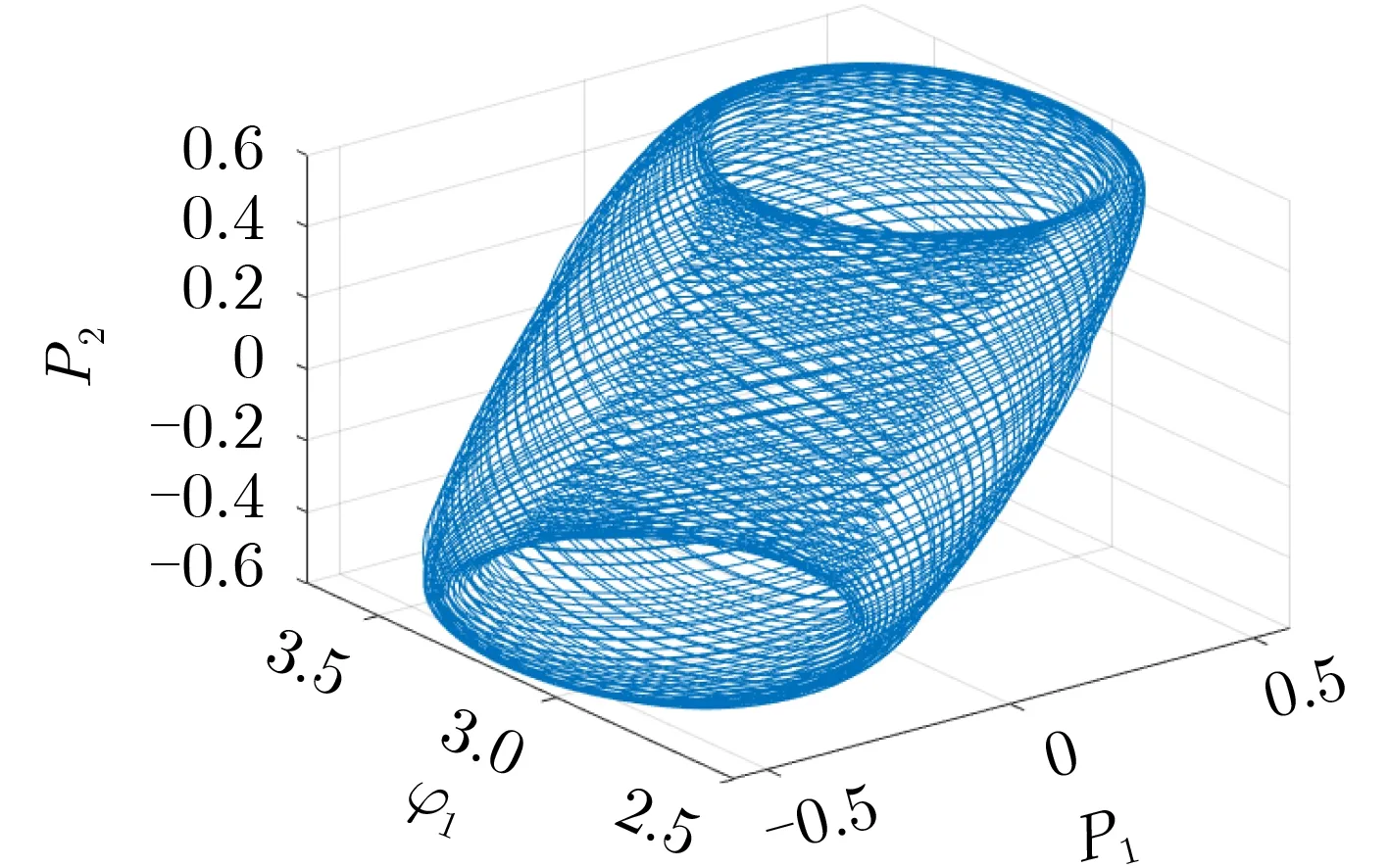
圖 1 量子細胞神經網絡中P 1, P 2, φ 1之間的軌跡曲線

圖3 新型量子圖像表示量子線路圖

2.3 量子Arnold變換

2.4 量子交換操作

在混淆像素位置之前，量子交換操作可以用于擴散圖像像素值來增強密文圖像的模糊性。量子交換操作Uxy的量子線路如圖4所示，其應用到某一個像素值|f(x,y)〉上的表示為

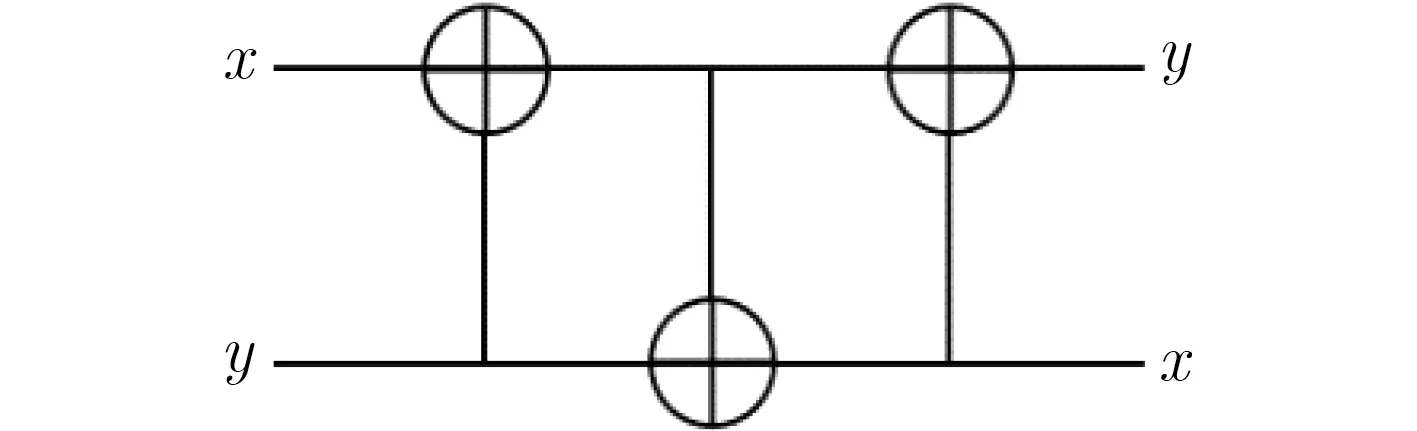
圖4 量子交換操作

3 量子灰度圖像加密和解密方法

本節將著重介紹基于量子細胞神經網絡的量子灰度圖像加密和解密步驟。整體加解密過程如圖5所示。圖5所涉及的量子細胞神經網絡超混沌同步技術可基于電路實現[36,37]，因此如何傳輸混沌信號(密鑰參數)將不再贅述。值得注意的是，在3.1節和3.2節所涉及的處理對象均針對圖像中的一個像素點。

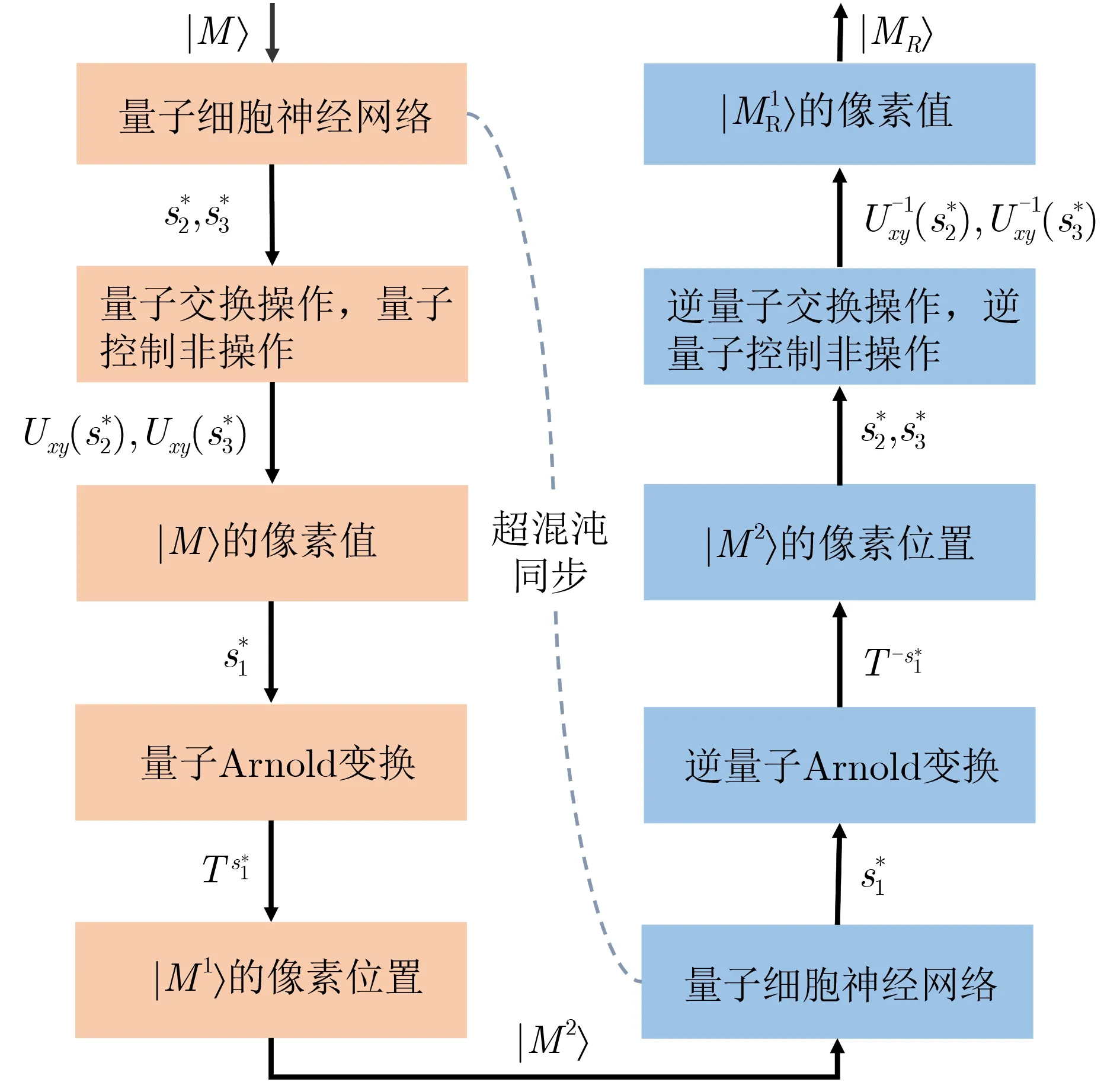
圖5 圖像加解密全過程

3.1 量子灰度圖像加密步驟

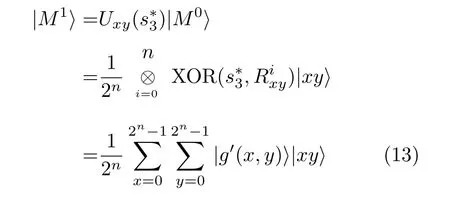
3.2 量子灰度圖像解密步驟

b1b2w1w2P1(0)

(1)獲取控制參數 , , , ，初始值 ,

4 仿真和理論分析

為了探求本方案的可行性及有效性，基于MATLAB平臺，本文對方案加解密過程進行了仿真實驗。所有的仿真實驗均基于同一個量子細胞神經網絡，并且給定的控制參數b1=b2=0.28,w1=0.7,w2=0.3 ， 初始值P1(0)=?0.348391961265269,P2(0)=3.18935060634640,φ1(0)=?0.0862955569903436,φ2(0)=5.76650621975721， 隨機起始點N0=8，信號取值間隔N=10000。圖6(a)、圖6(b)分別展示了512×512大小的原始圖像Woman和Pepper，圖6(c)、圖6(d)為Woman, Pepper加密后的圖像。

圖6 明文圖像Woman, Pepper及相應密文圖像

4.1 信息熵

信息熵(以下簡稱熵)是用于衡量一個圖像(系統)混亂程度的重要指標[37]，其數學表達為

4.2 直方圖分析

一個有效的圖像密碼算法應使不同密文圖像具有相似的直方圖。由圖7可知，明文圖像Woman和Pepper的直方圖很不一樣，但兩者對應的密文圖像直方圖幾乎一致，證明本方案具有有效性，能夠較好地抵抗直方圖攻擊。

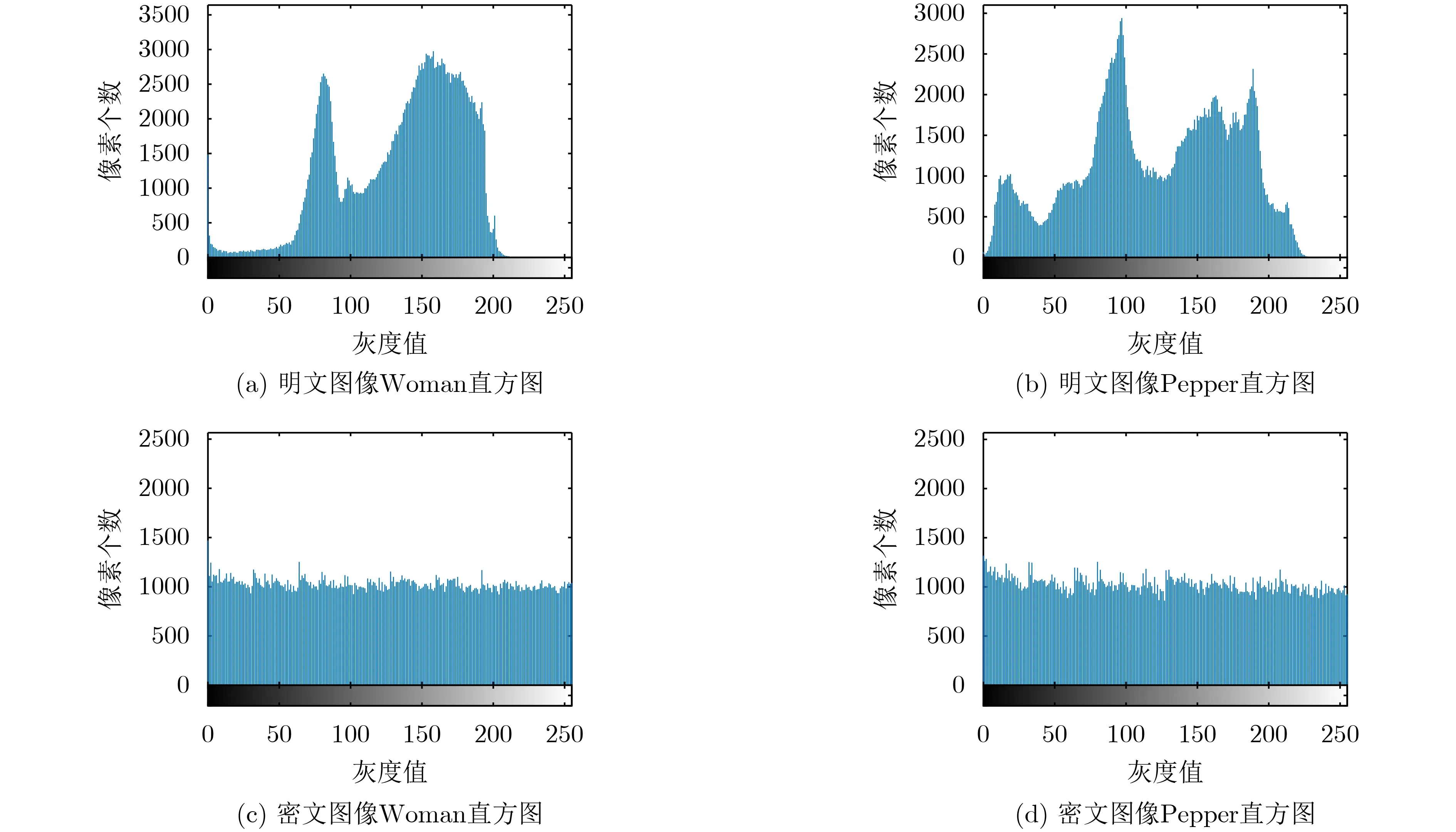
圖7 明文圖像Woman, Pepper及相應密文圖像的直方圖

表1 明文圖像及相應密文圖像的熵

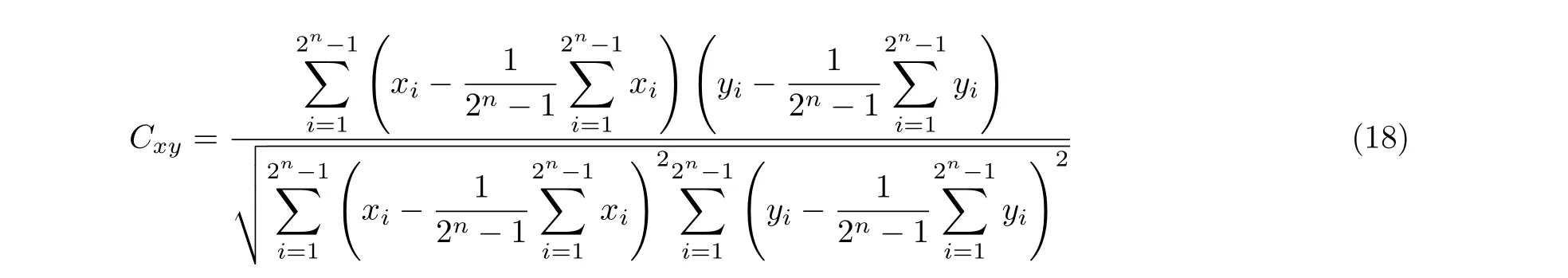
其中，xi和yi為鄰接像素。表2展示了明文圖像及相應密文圖像在水平、垂直、對角3個方向的相關性，從中可以看出，密文圖像鄰接像素相關性無論在哪個方向均接近于0。從圖8可以看出，明文圖像中鄰接像素聯系均很強-呈直線狀，但密文圖像中鄰接像素聯系均很弱-呈平鋪狀，證明本加密算法可強有力地混淆明文圖像以很好地抵抗統計攻擊。

圖8 圖像加密前后鄰接像素的聯系

表2 明文圖像及相應密文圖像在水平、垂直、對角方向的相關性

4.4 密鑰空間

對于圖像加密算法來說，密鑰空間需達到2100數量級才能較好地抵抗暴力攻擊[38]。本方案中，密鑰由b1,b2,w1,w2,P1(0),P2(0),φ1(0),φ2(0),N0,N構成。設非線性混沌系統中參數的有效精度為 1 0?14，結合本文中給出的實驗數據，本圖像算法的密鑰空間可達到 10120?2100。因此本方案具有巨大的密鑰空間可以抵抗經典計算機甚至量子計算機帶來的暴力攻擊及唯密文攻擊。

4.5 計算復雜度

4.6 密鑰敏感性分析

密鑰出現極其微小的改變從而導致獲得非理想的解密圖像，這種現象稱為強密鑰敏感性。密鑰敏感性可由直觀的解密圖像變化來評估。以明文圖像Lena為例，從圖9可以看出，即使密鑰有極小的偏移，也不能解密出正確的圖像，說明本方案具有較強的密鑰敏感性，能夠抵抗密鑰攻擊，證明了本方案的安全性。

圖9 不同密鑰情況下解密出的Lena圖像

5 結論

基于量子Arnold變換與量子邏輯操作，本文以確保圖像算法安全為基礎，利用超混沌系統量子細胞神經網絡增強加密過程中的不確定性和不可預測性，提出一種量子灰度圖像混沌密碼方法。其具有以下優勢：(1)為進一步模糊明文圖像，對明文圖像行像素值和列像素值均作了擴散處理。根據理論分析，本方案具有高安全性可以抵抗許多非法攻擊，如熵攻擊、統計攻擊；(2)為進一步降低圖像加密過程的計算復雜度，引入迭代量子Arnold變換、量子交換及量子控制非操作，將算法計算復雜度降為O(n)，為至今所提出的量子灰度圖像密碼方案中的較優值；(3)為進一步提高解密圖像質量，圖像加密操作全由可逆的量子邏輯門實現，在密鑰完全正確的情況下，本文方案能以較高保真度(100 dB)恢復出明文圖像。