High-temperature nodal ring semimetal in two-dimensional honeycomb-kagome Mn2N3 lattice

Xin-Ke Liu(劉鑫柯), Xin-Yang Li(李欣陽), Miao-Juan Ren(任妙娟),Pei-Ji Wang(王培吉), and Chang-Wen Zhang(張昌文)

School of Physics and Technology,University of Jinan,Jinan 250022,China

Keywords: first-principles calculation,semi-metal,nodal ring,Curie temperature

1. Introduction

Topological semimetals[1–4]are a recent research hotspot in the condensed matter physics. Many remarkable physical properties of graphene are related to its topological semi-metallic energy band structure, i.e., the conduction and valence bands of graphene intersect linearly at two isolated Fermi points in the Brillouin zone (BZ). The special energy band structure makes low-energy electrons the same as two-dimensional (2D) massless Dirac fermions.[5]The valence and conduction bands of topological semimetals can cross as dots or lines in the Fermi plane to form Dirac/Weyl semimetals[6–10]or nodal line/ring semimetals.Nodal ring semimetals (NRSM) form closed loops in thekspace where the conduction and valence bands cross continuously in the Fermi plane. NRSM[11–21]is firstly proposed in all-carbon Mackay Terrones crystals,[22]antiperovskite Cu3PdN[23]and other three-dimensional materials.Recently, the 2D NRSMs have received increasing attention,such as Ba2CdReO6[24]and Al3FeSi2.[25]Among them, the 2D monolayer Cu2Si[12]is experimentally confirmed to be an NRSM, and its energy band structure is characterized by two parallel rings centered at theΓpoint. NRSMs have many special properties, such as nondispersive Landau energy level,[26]high-temperature surface superconductivity,[27]and long-range Coulomb interactions.[28]Symmetry breaking may lead to the transformation of NRSM into other exotic topological states such as topological insulators and Weyl semimetals.[29,30]In general, the formation of ferromagnetic(FM) sequences is accompanied by time-reversal symmetry(TRS)breaking and sometimes by symmetry reduction of the crystal symmetry. Therefore, it is challenging to find NRSM in magnetic materials.

Studying 2D materials which have single-spin properties is notable when the TRS associated with spin is disrupted.[31]A semimetal is a state in which one electron spin channel is in a metallic state and the other electron spin channel is in an insulator or semiconductor.The speed of 100%polarized electrons or holes in a semi-metallic material is much faster than that of unpolarized electrons in a conventional 2D semiconductor,so it has a natural advantage in spin generation,injection and transport.By adjusting the gate voltage and exploiting the Hall effect,we can obtain a high-speed controlled flow of spin electrons, a property that can be used in devices such as field-effect transistors[32]and self-selecting filters.[33]Furthermore, it is possible that the spin-polarized NRSM materials are precursors of quantum anomalous Hall(QAH)phases that do not require magnetic atom doping,which can considerably expand the range of magnetic topology materials.[34–37]Investigating new materials with spin-polarized nodal rings(NR)is very intriguing,which will bring new practical applications in spintronics and condensed matter physics.

The 2D honeycomb-kagome(HK)lattice provides a fertile ground for the study of exotic physical properties, and previous studies have found some FM Dirac semimetals in the HK lattice.[38,39]In this work,our computational analysis yields that the HK monolayer Mn2N3possesses a fully spinpolarized NR that is strongly robust to spin–orbit coupling(SOC) interactions. The calculation of magnetic anisotropy energy (MAE) indicates that the ground state of the monolayer Mn2N3is out-of-plane(OP).The Curie temperature(TC)of Mn2N3is 530 K based on the Ising model and Monte-Carlo (MC) simulations. We next explain the origin of NR using wave function symmetry analysis and an effective tight-binding (TB) model constructed by the maximally localized Wannier function(MLWF).Furthermore, Mn2N3can construct h-BN/Mn2N3/h-BN heterostructures with h-BN and maintain its NRSM state, and the above conclusions demonstrate that the monolayer Mn2N3is an ideal material for spintronics devices.

2. Computational details

The Viennaab initiosimulation package (VASP),[40]based on the spin polarization density generalized functional theory (DFT), calculates all structural and electronic properties. We use Perdew–Burke–Ernzerhof (PBE) in the form of generalized gradient approximation (GGA)[41]to process the exchange–correlation function. Projection-augmented-wave(PAW)[42]potential is used to describe the ion–electron potential. To explain the Mn-3d orbital correlation effect, the structure is optimized by using a spin-dependent GGA plus HubbardU,[43]with the HubbardUparameter set to 3.0 eV.We test someUvalues and they show the qualitatively similar results. The screened Heyd–Scuseria–Ernzerhof Hybrid functional method(HSE06)is used to confirm the precision of the PBE calculation results. An 11×11×1 Monkhorst–Packk-points grid is used to integrate the BZ.[44]All the structural parameters are completely relaxed until the total energy and the Hellmann–Feynman force on each atom are converged to 10?6eV and 0.01 eV/?A,respectively. In order to avoid interactions induced by periodic images,a vacuum region exceeding 15 ?A is executed. Phonon dispersion curves of 3×3×1 supercells are calculated by using phonopy code[45]based on density functional perturbation theory. We use MC simulations and Ising model to calculate theTC.Ab initiomolecular dynamics(MD)calculations are calculated for a 5×5×1 supercell with a time step of 1 fs at 300 K temperature for 8 ps.We use D3 Grimme dispersion in the energy minimization process for the sake of finding the most mechanically stable conformation of the van der Waals(vdW)heterostructures.[46]The effective TB Hamiltonian is obtained by using the MLWF package[47,48]for fitting the energy bands.

3. Results and discussion

As seen in Fig.1(a),each HK monolayer Mn2N3contains two manganese(Mn)atoms and three nitrogen(N)atoms.The Mn atoms in the Mn2N3share an N bridge with neighboring Mn atoms and three N atoms around each Mn atom, forming a HK lattice withD6hpoint group symmetry. The crystal structure is similar to that of the 2D organic Ta2S3and Nb2O3[35]lattices. The relaxation lattice constant of Mn2N3isa1=a2=6.09 ?A. The N–Mn–N bond angle is 120?, and the Mn–Mn distance isd=3.52 ?A.To describe the stability of Mn2N3bonding, we calculate the cohesion energyEc, which is calculated as follows:

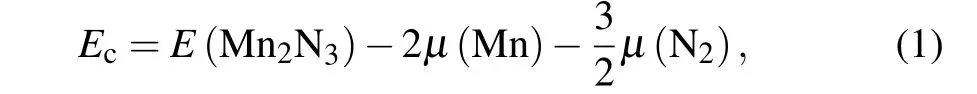
whereE(Mn2N3) is the energy of the Mn2N3andμ(Mn)andμ(N2) are the chemical potentials of Mn atoms and N2molecules, respectively. The cohesion energy of the Mn2N3isEc=?0.602 eV/atom, which is comparable to that of the monolayer CrI3(?0.903 eV/atom)[49]and Cr2Ge2Te6(?0.552 eV/atom).[50]The large cohesion energy indicates that the synthesis of the Mn2N3is an exothermic chemical reaction with stable bonding within the lattice. To illustrate the bonding properties of the Mn2N3,we calculate the electron localization function(ELF)in the(001)and(110)planes. As illustrated in Fig.1(b),the electrons are mainly localized around the N atom and almost no electrons are located around the Mn atom or in the central region between Mn and N. This indicates that the electrons are transferred from the Mn atom to the N atom, which is a typical ionic bonding property. The ionic bond between Mn and N is related to the large electronegativity difference between the bonding atoms.

The stability of the 2D materials is decisive for their experimental fabrication and deeper applications. In the first place, to demonstrate the kinetic stability of the Mn2N3, we calculate the phonon spectrum of the Mn2N3, as Fig. 1(d)shows. We can see that there are no imaginary frequencies in the full BZ,which indicates that the monolayer Mn2N3lattice is kinetically stable. In the second place, we use MD simulations to estimate the thermodynamic stability of the Mn2N3lattice. As depicted in Fig. 1(e), the crystal structure of the Mn2N3is not significantly deformed in the MD simulations within 8 ps at 300 K temperature. Last but not least,we calculate the elastic constants of the monolayer Mn2N3. The elastic constants can reflect the mechanical stability of the material.By using Voigt notation,the elastic tensorCof a 2D material withD6hpoint group symmetry can be simplified as

It is calculated thatC11andC12are equal to 32.47 GPa and 25.22 GPa, respectively. BothC11andC11?C12are greater than 0,which satisfy Born’s mechanical stability judgment criteria and confirm the mechanical stability of the monolayer Mn2N3. In conclusion, the above results indicate that the Mn2N3monolayers have very good structural stability and are promising to be prepared in the laboratory.

Fig.1.(a)Top and side views of the monolayer Mn2N3 lattice,where the Mn atoms are in red and the N atoms are in blue. (b)ELF maps of the(001)and(100) facets of the Mn2N3 lattice, with the charge aggregation distribution represented by normalized color mapping,blue for no charge present and red for charge concentration.(c)2D BZ representation of the monolayer Mn2N3.(d)Phonon spectrum of the monolayer Mn2N3. (e)MD simulation at 300 K temperature.

After demonstrating the structural stability of the Mn2N3,we next investigate the magnetic properties of the Mn2N3.The spin-polarized electronic properties can be illustrated by the differential electron density of the upper and lower spin channels. Spin polarization calculations show a net magnetic moment ofM=5μBper unit cell, indicating a large spin polarization in the Mn2N3. The local magnetic moment of the Mn atom isMMn=3.202μB,which is consistent with the high spin state of Mn3+. The nitrogen atoms have a very small opposite magnetic moment (MN=?0.47μB) due to the fact that they are antiferromagnetically coupled to the Mn atoms and are hardly magnetized. It is also evident from the spin density diagram in Fig.2(a)that the spin polarization is dominated by the Mn atom. To identify the magnetic ground state of the Mn2N3, we design some possible antiferromagnetic configurations,which include Neal antiferromagnetic(NAFM),stripe AFM (SAFM) and zigzag AFM (ZAFM), and FM, as illustrated in Fig. 2(b). The calculated energy of NAFM, SAFM,and ZAFM states is 37.33 meV,22.49 meV,and 13.47 meV,respectively, higher than that of FM state(?E=EAFM?EFM).So the Mn2N3ground state is the FM state.MAE describes the energy required to rotate the magnetization direction of the FM state from the magnetic easy axis to the magnetic hard axis,reflecting the difficulty of spin flip and the magnetic moment orientation in the ground state. We consider the SOC effect in the MAE calculations when calculating the energy for different magnetic moment orientations. MAE calculations show that the magnetic ground state of Mn2N3is in the OP [001]direction.

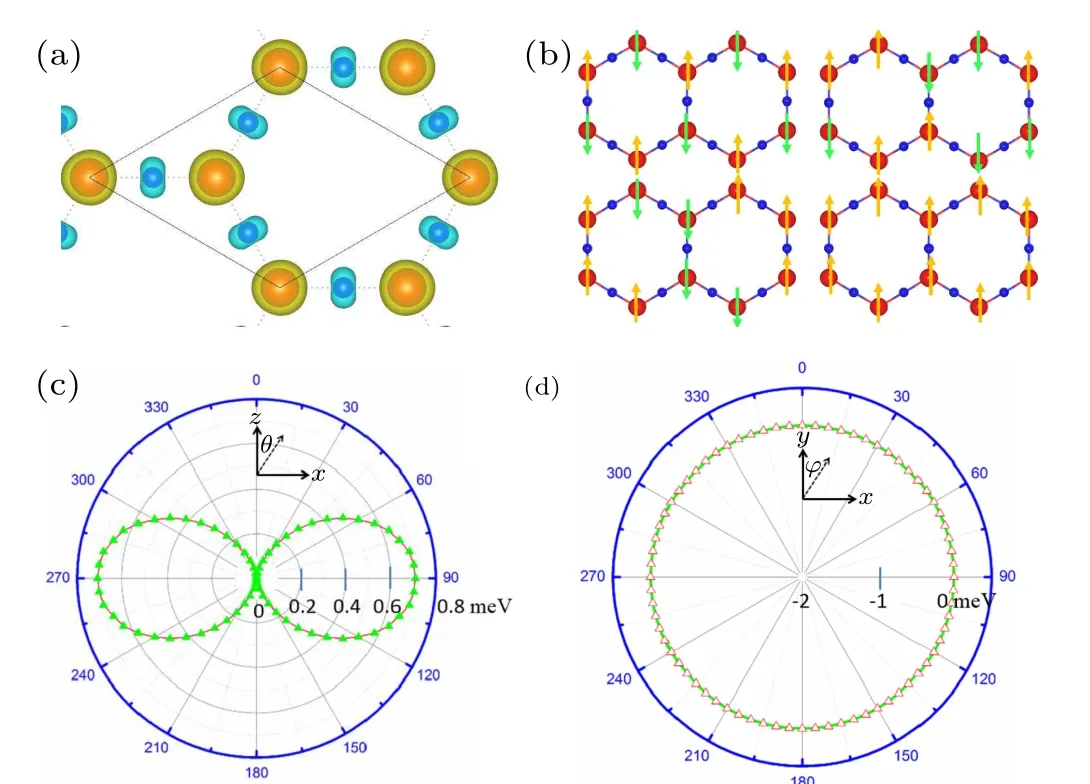
Fig. 2. (a) Spin density map of the (001) plane. (b) Four possible magnetic configurations of the monolayer Mn2N3:Upper left NAFM,upper right SAFM,lower left ZAFM,and lower right FM.(c)Difference between the energy of the magnetic moment in each direction from 0?to 360?in the xz plane θ and the base state energy. (d)Difference between the energy of the magnetic moment in each direction from 0?to 360?in the xy plane ? and the base state energy.

TheTCis another critical parameter for spintronic devices in practical applications.Before applying Mn2N3to spintronic devices, the relationship between the magnetic properties of the Mn2N3and temperature needs to be explored. By using the 2D Ising model to calculateTC, the spin Hamiltonian can be formulated as

whereJ1andJ2are respectively the nearest and second nearest neighbor parameters of the magnetic exchange interaction.Siis the atomic spin vector.Ais the anisotropy parameter, andSzis thez-component of the spin vector. Because of the larger distance between two second nearest neighbor Mn atoms (J2term is neglected) and the smaller MAE energy (Aterm is neglected), the spin Hamiltonian only considers theJ1term.TheJ1term can be expressed asJ1= ?E/(2zS2TM), where?E=EFM?EAFM,zis the number of nearest neighbor magnetic atoms,STMis the magnitude of the magnetic moment of the magnetic atom. The final value ofJ1is 6.1 meV andTCis 530 K. The red curve in Fig. 3 shows the image of the variation of the single-cell magnetic moment with temperature. The single-cell magnetic moment decreases significantly atTC=530 K which indicates that the maximum temperature at which the FM state can be maintained is 530 K.In addition,we calculate the specific heat capacity(CV)using the following equation:

whereEis the energy of each magnetic configuration. The calculatedCVis shown by the green curve in Fig. 3, which further confirms the ferromagnetic–paramagnetic phase transition with critical temperature of 530 K. The highTCindicates that the monolayer Mn2N3is a promising material for high-temperature spintronics.calculate the 3D energy bands and find that these crossings do not appear in isolation. On the contrary, they are part of two concentric rings centered at the pointΓas displayed in Figs.5(a)and 5(b). In Figs.5(c)and 5(d), we label the outer and inner rings asL1andL2, respectively. It is worth noting that theL1shape is a hexagon around theΓpoint. The hexagonalL1band crossings are anisotropic,which will bring many interesting phenomena.

Fig.4. (a)Electronic energy band diagrams of the upper spin(red)and lower spin(blue)channels of the monolayer Mn2N3 without considering SOC.(b)Analytical diagram of the orbital composition of the Mn atom, with the energy bands near the Fermi plane mainly contributed by dx2?y2, dyz, dxy orbitals. (c)Analytical diagram of the orbital composition of the N atom, the energy bands near the Fermi surface are mainly contributed by px+y, pz orbitals. (d)Electron energy band diagram(yellow)of the monolayer Mn2N3 with SOC.(e)Band structure calculated by the HSE06 method.(f)TB model fitted energy bands(black lines).

Fig. 3. MC simulation plot with red indicating the magnetic moment magnitude versus temperature curve and green indicating the specific CV versus temperature curve.

We next investigate the electronic properties of the monolayer Mn2N3. The first one,in Fig.4(a),the electronic bands with spin up and spin down are shown in blue and red, respectively. As can be seen,the electrons near the Fermi plane are completely separated from each other, and the spin-down electrons carry a wide band gap of 2.08 eV,whilst the spin-up electron band has no band gap. Consequently, in the vicinity of the Fermi energy level, the electrons are fully spinpolarized. The second one is that we observe a linear crossing of the three energy bands near the Fermi energy level. In these three energy bands,one is an electron-like band(marked asγband), the other two are hole-like bands (marked asαandβbands), and band crossover occurs betweenγband andα,βbands. In the projection of the orbitals in Figs.4(b)and 4(c),it is observed that theαandβbands are largely attributed to the Mn(dxy,dx2?y2), N(px+y) orbitals, whereas theγband is mostly contributed by the Mn(dyz),N(pz)orbitals. We further

Then we calculate the electronic properties after considering the SOC effect. The yellow line in Fig. 4(d) shows the electronic energy band diagram along theM–Γ–K–Mpath after considering the SOC effect. It is worth noting that the energy band along theM–Γ–K–Mpath under the SOC effect is not opened with a gap. We also examine the other parts of both NR and no band gaps are found to exist. The above results indicate that the NR in the monolayer Mn2N3is stable to SOC.In addition,to verify the accuracy of the PBE calculation results, we calculate the HSE06 energy band using the accurate and reliable HSE06 hybrid function algorithm, as shown in Fig.4(e). It can be seen from the figure that onlyL1opens a tiny band gap of 10 meV in theΓ–Kpath, which has little effect on the application of the nodal ring, and the results of the HSE06 and PBE calculations are qualitatively the same.

Fig.5. (a)The monolayer Mn2N3 3D energy band. (b)The NR formed by the intersection of α, β, and γ bands, with the outer ring defined as L1 and the inner ring defined as L2. (c)Top view of the NR L1. (d)Top view of the NR L2.

Then,it is natural to wonder what protects the NR in the monolayer Mn2N3. Through analysis of the symmetries for the three bands, we believe that NR is protected by horizontal mirror(Mz)symmetry. The ground-state magnetization direction is perpendicular horizontal facing outward, such that the magnetization direction does not destroy theMzin the FM state. TheMzeigenvalues of the two hole-like bandsαandβare +i, while theMzeigenvalues of the electron-like bandγare?i, so theγband must cross theαandβbands without hybridization.As long asMzis present,the energy band crossing will not open the band gap even under SOC action,and NR is thus protected. Next, we construct TB model Hamiltonian by projecting the dxy,dx2?y2,and dyzorbitals of the Mn atoms and px+yand pzof the N atoms onto the Mn2N3cell using the MLWF for further analysis of the energy band structure.As indicated in the black line in Fig. 4(f), the main features of the DFT calculated energy band considering SOC and the TB model fitted energy band around theEflevel are the same,despite the subtle differences. Furthermore,because of theMzsymmetry, the eigenstates have to be spin-polarized oriented along the OP, i.e., no hybridization occurs in the spin-up and spin-down energy band,and those energy bands are fully spinpolarized. In summary,the monolayer Mn2N3is a novel material protected byMzwith fully spin-polarized NR under the action of SOC. It is not difficult to infer that when breakingMz,NRs will also be broken. To verify the above conjecture,we rotate the magnetic moments toθ=45?andθ=90?directions, respectively, and calculate their energy band diagrams.As presented in Fig. 6, since theMzsymmetry is broken, the energy band crossover is opened and the NRs is destroyed into two pairs of Weyl points.

Finally, since growing thin films on the semiconductor substrates with large band gaps is a common practice for experiments, we explore the feasibility of forming heterostructures with a single layer of the Mn2N3on semiconductor substrates. From the stress–energy band diagram in Fig.8,it can be seen that the Mn2N3lattice nodal ring property is robust to compressive stresses and maintains the nodal ring energy band characteristics even at 2% tensile stress. We place Mn2N3on the h-BN[51]substrates to form h-BN/Mn2N3/h-BN heterostructures, as showed in Fig.7(a). Structural optimization considering van der Waals corrections shows that the layer spacing between the Mn2N3and the h-BN is 3.0 ?A,which is typically of weak vdW interactions. Figure 7(b) shows the electronic energy band structure of the heterostructures. We can see that the energy band structure and FM properties of the Mn2N3can be well maintained on the h-BN/Mn2N3/h-BN heterostructures,and the NR near theEflevel is essentially the same as that of monolayer Mn2N3. This is due to the preservation of theMzmirror symmetry by placing the monolayer Mn2N3between two h-BNs.

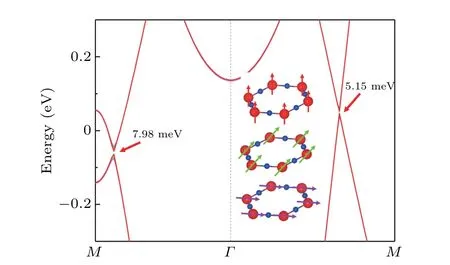
Fig. 6. The energy band diagrams when the direction of the magnetic moment is along θ =0?,θ =45?,and θ =90?are shown in red,green,and purple,respectively.

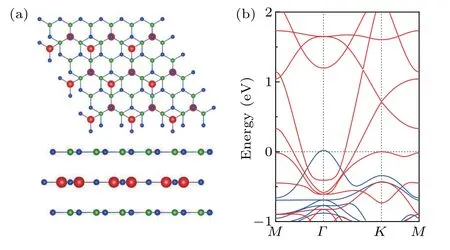
Fig. 7. (a) Top and side views of the h-BN/Mn2N3/h-BN heterostructures,where the N atom is directly above the Mn atom. (b) Electron energy band diagram of the heterostructures.

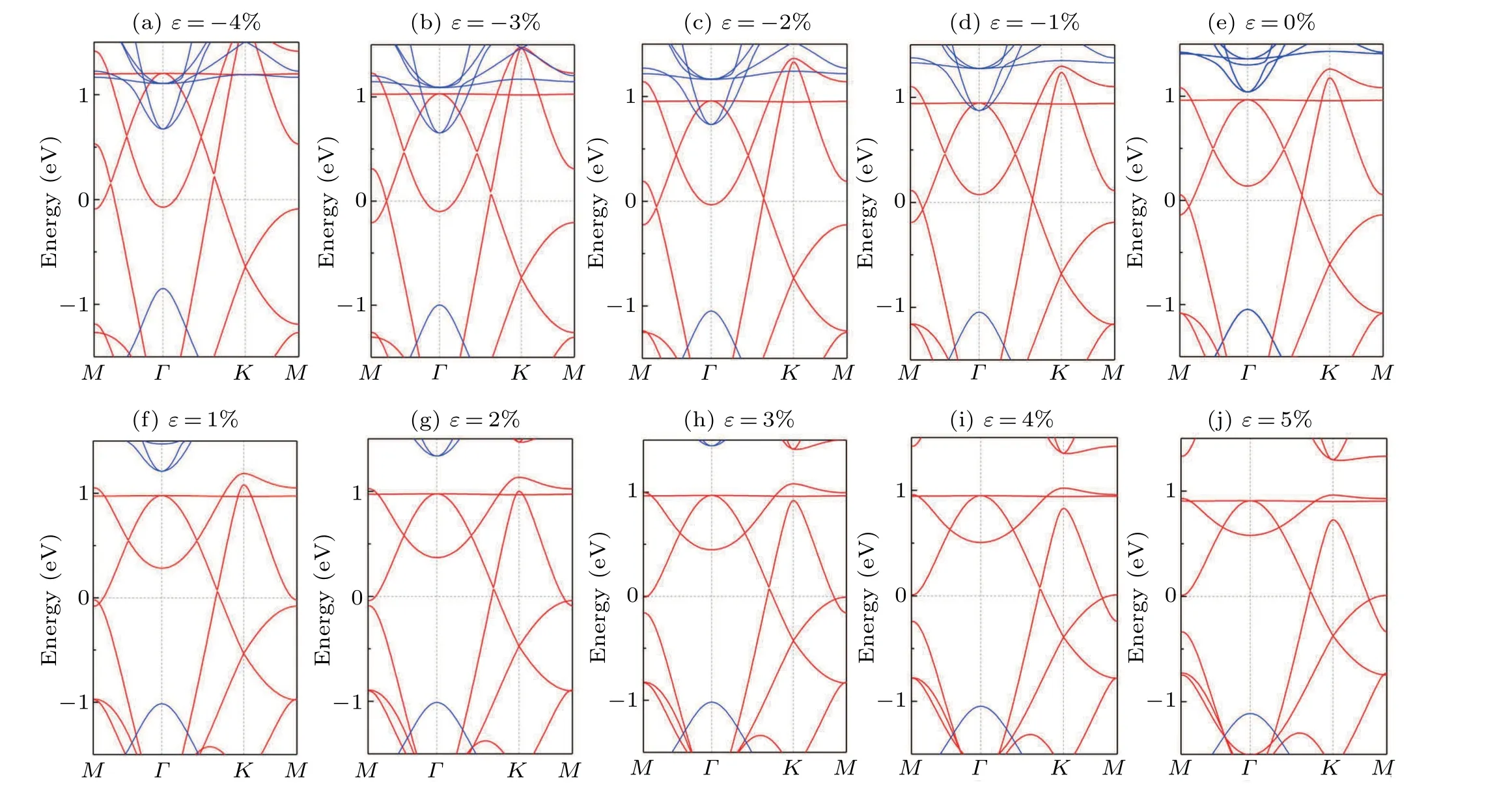
Fig.8. Band structures of the Mn2N3 under different biaxial strain.

4. Conclusion and perspectives

We propose that the 2D monolayer Mn2N3is a FM NRSM, which has thermodynamical and kinetical stability.Based on the Ising model and MC simulations,aTCof 530 K is obtained,higher than that of most of the found 2D NRSMs.Analysis of the electron energy band structure shows that the electron and hole bands with the same spin component are in linear contact with each other near theEfto form two NRs centered at theΓpoint. There are much faster spin-polarized carriers in the monolayer Mn2N3than that of in the non-spinpolarized materials. Because of the protection ofMzsymmetry,NR is robust to SOC.Then we elucidate the origin of NR by symmetry analysis and TB model. Finally,we demonstrate that the monolayer Mn2N3can form h-BN/Mn2N3/h-BN heterostructures with h-BN and maintain NR properties. The 2D Mn2N3is a promising candidate for the experimental observation of spin-polarized NR fermions and gives a motivating platform to design new spintronics devices.

Acknowledgments

Project supported by Taishan Scholar Program of Shandong Province, China (Grant No. ts20190939), Independent Cultivation Program of Innovation Team of Jinan City(Grant No. 2021GXRC043), and National Natural Science Foundation of China(Grant Nos.52173283 and 62071200).