基于差值法的實心鉚釘緊固壓力和壓強測量方法
劉 澤,劉 松,蘇佳文
(中國直升機設計研究所,江西 景德鎮 333001)
0 引言
鉚接具有連接構件強度穩定可靠、工藝過程簡單、質量檢查和排故比較容易及對裂紋損傷有一定的止裂作用等優點,在飛機裝配中得到了廣泛應用[1]。與抽芯鉚釘相比,實心鉚釘在鉚接成型過程中,釘桿在鉚槍的沖擊力作用下膨脹變形,將釘孔完全填充形成緊密配合;釘桿端部在擋鐵阻擋下鐓粗變形形成鐓頭,可有效緊固被連接構件,具有更高的鉚接強度[2];且其制造成本更加低廉,在飛機鉚接裝配中使用量巨大。目前鉚接方面大部分的研究集中在鉚釘抗剪力學性能分析、鉚接過程中鉚釘的變形、受載規律和鉚釘排布優化設計[3-9],少部分對鉚接后的殘余應力進行了分析。但由于很難進行試驗測量,上述研究主要為有限元仿真分析[10],目前尚無測量鉚釘的緊固壓力和壓強的試驗方法。實心鉚釘的緊固壓力和壓強影響連接結構的鉚接強度,因此,設計試驗測量方法,了解實心鉚釘的緊固壓力和壓強的情況,對研究實心鉚釘的鉚接強度校核方法具有重要的工程參考價值。
基于上述原因,本文提出了一種實心鉚釘的緊固壓力和壓強測量方法,該方法基于差值法間接測量;設計了測量試驗,給出了試驗件的結構和設計要求,詳細說明了試驗設備、試驗原理及試驗測量內容;基于試驗測量的摩擦力矩,利用差值法推導了普通型實心鉚釘和沉頭實心鉚釘的的軸向緊固壓力和徑向壓強的計算公式。
1 實心鉚釘的緊固壓力和壓強測量試驗
1.1 試驗件
圖1為試驗件1結構示意圖,為帶凸臺結構零件,其中凸臺帶有鉚釘孔。圖2為試驗件2結構示意圖,為長條形板,其中一端為半圓形且帶有鉚釘孔,試驗時與試驗件1凸臺部分鉚接,如圖3所示。試驗件2寬度D0要略大于試驗件1凸臺直徑D。本試驗通過測量試驗件1凸臺部分與試驗件2之間的摩擦力矩間接換算出實心鉚釘的緊固壓力和壓強,需要假設兩試驗件接觸面內的壓強各點相等。因此,在空間能夠滿足鉚接的情況下,凸臺直徑D應盡量小。試驗件1的凸臺和試驗件2板應具備一定厚度(分別為h,h0),以保證擁有足夠的剛度,避免試驗時產生過大變形。對于常用的Φ4 mm鉚釘,試驗件厚度達到3 mm即能滿足剛度需求。本文將鉚釘的釘頭設計在試驗件1一側。

圖1 試驗件1結構示意圖
通過差值法推導求解實心鉚釘的緊固壓力和壓強,因此規定試驗件1與試驗件2的材料相同,且具有2種表面狀態(改變試驗件的表面粗糙度或鍍層等條件),并規定在不同組合下,試驗件1與試驗件2相互之間的摩擦系數分別為μ、μ′和μ″,具體見表1。

圖2 試驗件2結構示意圖

圖3 試驗件1與試驗件2鉚接示意圖

表1 摩擦系數
1.2 測量試驗
圖4所示為實心鉚釘的摩擦力矩測量試驗示意圖。在試驗臺架上安裝可調功率電機,將試驗件1和試驗件2鉚接并按圖示固定安裝在電機和臺架上,試驗件2與臺架連接端部接有力傳感器,L為連接端部距鉚釘中心距離。試驗時,緩慢增加電機輸出功率,使試驗件1由靜止向勻速轉動,測得最大力值F0。因此,試驗件1和試驗件2之間摩擦力產生的總力矩為:
M=LF0
(1)

圖4 摩擦力矩測量試驗示意圖
測量試驗件1和試驗件2不同表面狀態組合下的摩擦力矩M(1)、M(2)、M(3),具體見表2。

表2 摩擦力矩測量
2 軸向緊固壓力和徑向壓強計算公式
圖5為實心鉚釘鉚接示意圖。設軸向緊固壓力為N,徑向壓強為P,釘孔的圓柱面積為S0,則徑向壓強產生的擠壓力:
N′=PS0
(2)
釘孔為光滑的金屬內壁,其與釘桿的摩擦系數可由相應等效試驗測量,此處設其為v。

圖5 實心鉚釘鉚接示意圖
2.1 普通型實心鉚釘
如圖6所示,設鉚釘的直徑為d,釘頭直徑為d1,鐓頭直徑為d2。設試驗件1和試驗件2之間的摩擦力的力矩為M1,如圖7所示,采用積分計算。
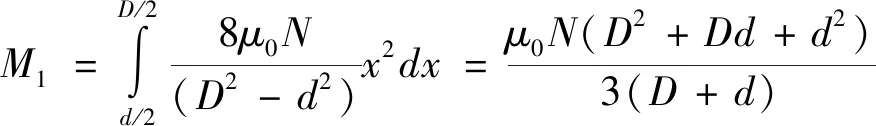
(3)
式中,μ0根據兩試驗件接觸面情況取值(μ、μ′或μ″)。
徑向擠壓力N′如圖8所示,摩擦力沿切線方向,因此N″產生摩擦力的力矩:

(4)
設釘頭和鐓頭與試驗件之間的摩擦力的力矩為M3,釘頭和鐓頭與試驗件摩擦區域的外徑分別為d1和d2,由M1推導可知:

(5)
式中,μ1為釘頭與試驗件1之間的摩擦系數,μ2為鐓頭與試驗件2之間的摩擦系數,可由等效試驗測量;為便于公式推導的整齊化,對于3組摩擦力矩測量試驗,對應的摩擦系數μ1、μ2采用表3的表示方式。

表3 摩擦系數μ1和μ2

為簡化公式形式,令:

(6)

(7)

(8)
由力矩平衡有:
M=M1+M2+M3
(9)
對同種鉚釘,當鉚釘直徑d相同時,摩擦力矩M2相同,因此,當按表2進行試驗時,有:
M(1)=N[λ0μ+λ1μ1(1)+λ2μ2(1)]+M2
(10)
M(2)=N[λ0μ′+λ1μ1(2)+λ2μ2(2)]+M2
(11)
M(3)=N[λ0μ″+λ1μ1(3)+λ2μ2(3)]+M2
(12)
式(11)-式(10),式(12)-式(10),式(12)-式(11),則有:
N(1)=

(13)
N(2)=

(14)
N(3)=

(15)
式中,N(1)、N(2)、N(3)為3次差值求得的軸向緊固壓力,對其求平均:

(16)
將軸向緊固壓力N帶入式(10)、式(11)、式(12),求得徑向擠壓力:
N′(1)=

(17)
N′(2)=

(18)
N′(3)=

(19)
對其求平均:

(20)
將N′帶入(2)式求得徑向壓強P。
2.2 沉頭實心鉚釘
如圖9所示,沉頭鉚釘的沉頭度數為θ,沉頭深度為w,鐓頭的直徑為d3,試驗件上的沉頭锪窩也為光滑的金屬內壁,因此,鉚釘沉頭與锪窩之間的摩擦系數為v;同樣設試驗件1和試驗件2之間的摩擦力的力矩為M1,徑向擠壓力N′產生的摩擦力的力矩為M2,設沉頭釘頭和鐓頭與試驗件之間的摩擦力矩為M3;由(3)式和(4)式可知,沉頭鉚釘的摩擦力矩M1和M2與普通型鉚釘的計算公式相同,因此,僅需推導M3的計算公式。
對于沉頭鉚釘,沉頭所受的鉚接壓力需進行分解,如圖10所示,沉頭的垂直壓力為:

(21)

沉頭側面積:

(22)
鐓頭與試驗件2之間的摩擦力的力矩與普通型鉚釘的計算相同,如圖11所示。沉頭部分則通過積分計算:
M3=

(23)

圖11 沉頭摩擦力力矩計算
為簡化公式形式,令:

(24)

(25)
滿足式(9)平衡方程,且對同種鉚釘,當鉚釘直徑d相同時,摩擦力力矩M2相同,因此,當按表2進行試驗時,有:
M(1)=N[λ0μ+λ3+λ4μ2(1)]+M2
(26)
M(2)=N[λ0μ′+λ3+λ4μ2(2)]+M2
(27)
M(3)=N[λ0μ″+λ3+λ4μ2(3)]+M2
(28)
式(27)-式(26),式(28)-式(26),式(28)-式(27),則有:
按(16)式對N求平均后帶入式(26)、式(27)、式(28),求得徑向擠壓力:

(32)

(33)

(34)
按(20)式計算N′平均值,帶入(2)式求得徑向壓強P。
3 試驗件厚度和摩擦系數設計要求
上述試驗測量方法是基于所有摩擦力矩均達到最大值,因此有:
M2(試驗件1)+M3(試驗件1)=
M2(試驗件2)+M3(試驗件2)
(35)
式中,M2(試驗件1)、M2(試驗件2)分別為試驗件1、試驗件2與釘桿的摩擦力矩,M3(試驗件1)為試驗件1與釘頭的摩擦力矩,M3(試驗件2)為試驗件2與鐓頭的摩擦力矩。
對于普通型實心鉚釘,式(35)為:

(36)
存在N和N′兩個未知量,當h=h0時可消除兩未知量,則有:
式(37)即普通型實心鉚釘摩擦系數的理想條件,在試驗設計中盡量保證等式左右數值相近,以減小試驗測量誤差。
對于沉頭實心鉚釘,式(35)為:

(38)
當時h=h0,則有:

(39)
因此,試驗件1和試驗件2厚度相等。為減小試驗測量誤差,普通型實心鉚釘和沉頭實心鉚釘應盡量保證(37)式、(39)式等號兩側的數值相近。
4 結論
針對目前實心鉚釘的緊固壓力和壓強尚無試驗測量方法這一問題,本文提出了一種基于差值法的間接測量方法,具體如下:
1)設計了實心鉚釘鉚接的摩擦力矩測量試驗,給出了試驗件的結構和設計要求,詳細說明了試驗設備、試驗原理及試驗測量內容;
2)基于試驗測量的摩擦力矩,利用差值法間接計算實心鉚釘的緊固壓力和壓強,由摩擦力力矩平衡,推導了普通型實心鉚釘和沉頭實心鉚釘的軸向緊固壓力和徑向壓強的計算公式;
3)采用旋轉法測量總摩擦力矩,在試驗過程中,鉚釘僅受到軸向緊固壓力、徑向擠壓力和摩擦力作用,保證了試驗測量的有效性和準確性;
4)計算公式中考慮了試驗件1和試驗件2、釘頭和試驗件1、鐓頭和試驗件2、釘桿和釘孔的摩擦力力矩,與實際鉚接情況相同,保證了計算公式的有效性和準確性。

