基于Spark的并行反向k最近鄰查詢

楊澤雪，張 毅，李 陸，劉偉東，蔣 超

(1.東北林業大學 信息與計算機工程學院，黑龍江 哈爾濱 150040；2.黑龍江省政務大數據中心 合作交流與創新發展處，黑龍江 哈爾濱 150028；3.黑龍江工程學院 計算機科學與技術系，黑龍江 哈爾濱 150050)

0 引 言

隨著數據量的爆炸式增長，研究分布式環境下的并行反向k最近鄰(reverseknearest neighbor，RkNN)查詢[1]受到研究人員的關注。

目前流行的并行處理框架主要包括MapReduce和Spark。而當前的并行RkNN查詢算法大多數都是基于Map-Reduce[2-5]框架。文獻[6]介紹了基于倒排網格索引(inver-ted grid index)的分布式RkNN查詢處理方法。文獻[7]在Hadoop的空間擴展框架SpatialHadoop上進行了分布式RkNN查詢研究，給出了基于SpatialHadoop的RkNN查詢算法，并在真實數據集上實現了該算法。文獻[8]提出了基于SpatialHadoop的RkNN查詢MRSLICE算法。基于Spark框架的分布式空間查詢研究，近年來國內外學者提出了GeoSpark[9]、SpatialSpark[10]、LocationSpark[11]等框架，這些框架可實現基于Spark的分布式空間范圍查詢、kNN查詢和空間連接查詢，并且通過實驗驗證基于Spark框架的查詢處理優于MapReduce框架。除以上典型空間查詢之外，學者們擴展了基于Spark框架的變體查詢研究，包括距離連接查詢[12,13]、時空連接查詢[14,15]、top-k空間連接查詢[16]、軌跡k近鄰查詢[17]、空間范圍查詢[18]、k近鄰連接查詢[19]、組k近鄰查詢[20]等。

以上研究均展示了Spark框架處理并行空間查詢的優越性。但是，基于Spark框架的RkNN查詢研究較少，文獻[7]提出了基于LocationSpark的并行RkNN查詢算法，并將該算法與基于SpatialHadoop的RkNN查詢算法進行了比較，結果顯示基于LocationSpark的并行RkNN算法明顯優于SpatialHadoop。為此本文基于Spark框架研究并行RkNN查詢，基于Voronoi圖在空間鄰近性方面的優良特性，在Spark框架上擴展基于Voronoi圖的并行索引結構Grid-Voronoi-Index，在該索引結構上給出基于Spark的RkNN查詢處理算法SV_RkNN，進一步提高并行RkNN的查詢效率。

1 相關定義

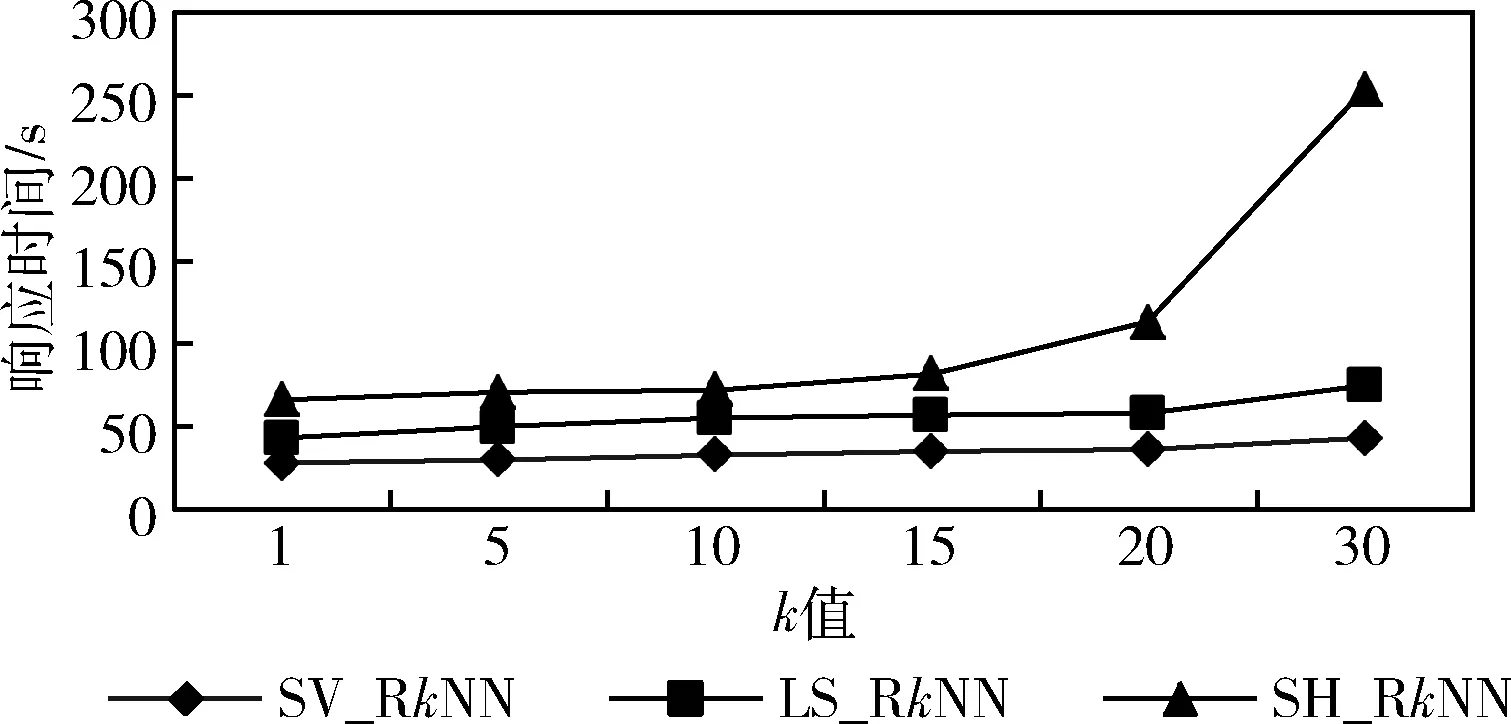
定義3[2]Voronoi圖：給定一個點集P={p1,…,pn}， 其中2

定義4[2]k級鄰接生成點：給定一組生成點P={p1,…,pn} 生成的Voronoi圖中，其中2

AGk(pi)={pj|VP(p) 與VP(pj) 有公共邊，p∈AGk-1(pi)}

定理1[21]給定數據集P的Voronoi圖VD(P)和查詢點q，其中q∈P， 查詢點q的R1NN在其1級鄰接生成點中。

推論1 給定數據集P的Voronoi圖VD(P)和查詢點q，其中q∈P，查詢點q的RkNN在其前k級鄰接生成點中。

定理2[22]給定數據集P和查詢點q，在點q處將空間區域6等分(每個部分60°)，則每個區域中查詢點q的RkNN只能在其k近鄰中。

2 基于Spark的索引構建

2.1 基于Spark的索引構建過程

為了完成并行反向k最近鄰查詢，構建雙層索引結構，即全局索引和局部索引，全局索引采取網格索引，存放在master節點中，全局索引通過網格的劃分將數據切分成各個數據塊，然后在各個數據塊上建立局部索引，局部索引采用Voronoi圖索引結構，存儲在各個worker結點中。基于Spark的網格-Voronoi圖雙層索引構建過程如圖1所示。

圖1 基于Spark的網格-Voronoi圖雙層索引結構

2.2 基于Spark的雙層索引構建算法

給定大規模數據集dataset，讀取數據文件生成dataRDD并分配到各個分區中，此時的數據分區并沒有考慮到空間數據的鄰近性，而分區的數據關系直接影響到后續查詢的性能。為此，將dataRDD重新分區，以保證數據的鄰近關系。為此建立雙層索引結構，首先對于dataRDD每個分區的數據進行采樣，這里選取1%的數據，將這些數據傳送到主結點生成網格索引GridIndex，然后利用網格索引將每個分區中的數據分配到對應的網格中，對于每個分區中的數據點，如果該數據點包含在某個網格中，就將其分到該網格中，分配結果生成新的網格分區RDD即GridPartitionRdd，然后將GridPartitionRdd中具有相同grid_id的數據重新分配到新的分區中，也就是進行再分區，對于每一個新的分區中的對象，分別建立Voronoi索引，形成VoronoiIndexRdd。

基于Spark的網格-Voronoi 圖雙層索引構建算法如算法1所示。

算法1：Grid-Voronoi-Index-Construct

輸入：數據集dataset;

輸出：局部Voronoi圖索引，全局網格索引;

begin

sc←new SparkContext(conf);

dataRDD←sc.textfile(dataset);

//加載原始數據

SampleData←dataRDD.sample;//對原始數據進行并行采樣

GridIndex←SampleData.CreateGridIndex;

//基于采樣數據，在master結點構建網格索引

for each partition do

for each point in dataRDD do

for each grid do

If point∈grid then

GridPartitionRdd←

GridPartitionRdd∪(grid_id,point);

//將dataRDD中的點分配到對應網格中

endif

endfor

endfor

endfor

rePartitionRdd←GridPartitionRdd.partitionBy

(GridPartitionRdd(grid_id,point)

?rePartitionRdd(grid_id,point)

//將具有相同grid_id的數據混洗到同一個分區中

for each partition do

VoronoiIndexRdd←rePartitionRdd.map

(rePartitionRdd(grid_id,point)?

VoronoiIndexRdd(grid_id,PVDi));

endfor

VoronoiIndexRdd.merge();

VoronoiIndexRdd.cache();

GridIndex.cache();

return GridIndexRdd;

return VoronoiIndexRdd;

end

3 基于Spark的并行反向k最近鄰查詢

3.1 基于Spark的并行反向k最近鄰查詢過程

基于Spark的并行反向k最近鄰查詢處理過程如圖2所示。

圖2 基于Spark并行空間反向k最近鄰查詢處理流程

該查詢方法首先載入數據集的全局網格索引，通過網格索引的檢索，查找出包含查詢點q的局部Voronoi圖索引，加載局部Voronoi圖索引，并啟動任務開始執行。然后在每個分區中執行在基于Voronoi圖的RkNN過濾-精煉算法，找到查詢點q的RkNN，形成結果存儲在HDFS中。

3.2 基于Voronoi圖的RkNN過濾-精煉算法

給定數據集P的Voronoi圖VD(P)和查詢點q，基于Voronoi圖的RkNN過濾-精煉算法包含過濾和精煉兩個步驟。首先，由過濾步驟獲得可能成為結果的候選，在Voronoi圖VD(P)中定位查詢點q，在q處將空間劃分為6等分區域，由推論1可知，查詢點q的RkNN一定在其前k級鄰接生成點中，再由定理2可知，每個6等分區域的RkNN結果只能在其k近鄰中，因此對于每個區域，將q的前k級鄰接生成點放入候選集中；然后，由精煉步驟去除候選集中不能成為結果的候選，計算候選集中每個點p的第k個最近鄰k-thNN，如果p與k-thNN之間的距離小于p與q之間的距離，則從候選集中刪掉p，最后將6個區域的候選集合并即為最終結果。

基于Voronoi圖的RkNN過濾、精煉算法如算法2、算法3所示。

算法2： VRkNN-Filter(P,q,k)

輸入： 查詢點q， 數據點集P的Voronoi圖VD(P)， RkNN的k值;

輸出： RkNN的候選集Scnd(i);

begin

fori=1 to 6 do

Scnd(i)←?；

endfor

在VD(P)中定位查詢點q;

SixRegionPartition(P)；

for eachScnd(i) do

for i=1 tokdo

Scnd(i)←Scnd(i)+AGi(q)；

//將q的第i級鄰接生成點加入候選集中

endfor

returnScnd(i)；

end

算法3： VRkNN-Verification(P,q,k)

輸入： 查詢點q， 數據點集Voronoi圖VD(P)， RkNN的k值;

輸出： RkNN結果集result;

begin

Scnd(i)←VRkNN-Filter(P,q,k)；

Scnd←?；

result←?；

for each pointpinScnd(i) do

pk=k-th NN ofp；

if dist(p,q)>dist(p,pk) then

Scnd(i)←Scnd(i)-p；

endif

endfor

Scnd←Scnd∪Scnd(i)；

result←Scnd；

returnresult；

end

定理3 算法VRkNN-Filter(P,q,k) 和VRkNN-Verification(P,q,k) 可以正確地查找查詢點q的反向k最近鄰，算法VRkNN-Filter(P,q,k) 和VRkNN-Verification(P,q,k) 是可以終止的，算法的時間復雜度是O(nlogn)。

證明：(正確性)算法VRkNN-Filter(P,q,k) 首先將空間區域以查詢點q為中心進行6等分，然后在每個區域中查找q的k個最近鄰，將這些結果放入候選集中，由推論1和定理2可知，算法VRkNN-Filter(P,q,k) 中的結果是正確的。算法VRkNN-Verification(P,q,k) 對候選集中的每個數據點進行處理，用該點的第k個最近鄰與之對比，如果滿足該點與查詢點的距離大于該點與其第k個最近鄰的距離，則去掉該候選，逐個去除錯誤的候選，得到正確的結果。

(可終止性)算法VRkNN-Filter(P,q,k) 對6個空間區域分別進行for循環，循環次數為k，是有限的，為此算法2是可終止的，算法VRkNN-Verification(P,q,k) 中的for循環是針對候選集中的對象的，數據也是有限的，所以循環是可以終止的，為此算法3也是可終止的。

(時間復雜度分析)算法VRkNN-Filter(P,q,k) 計算Voronoi圖的時間復雜度為O(nlogn)，在VD(P)中定位查詢點q時間是O(logn)，查找k個最近鄰時間為O(klogn)， 為此算法2的時間復雜度為O(nlogn+klogn)； 算法VRkNN-Verification(P,q,k) 針對候選集中對象進行查詢，假設候選集中對象個數為m，則查詢時間為O(mlogn)，為此算法3的時間復雜度為O(mlogn)，綜上，基于Voronoi圖的RkNN過濾-精煉算法總的時間復雜度為O(nlogn+klogn+mlogn)。 證畢。

3.3 基于Spark并行反向k最近鄰查詢算法

基于Spark的并行反向k最近鄰查詢算法SV_RkNN基本思想如下：算法包括兩個步驟，第一個步驟為過濾，第二個步驟為精煉。給定雙層索引結構的RDD，算法首先查詢全局網格索引，定位查詢點q所在網格，確定對應局部索引，在局部索引RDD所在分區執行過濾精煉步驟。過濾步驟執行VRkNN-Filter過濾算法，執行過程中如果出現候選集中的點在相鄰的其它分區時，如圖1的點p1的某些最近鄰p2、p3在其相鄰的分區中，需要對相應分區進行并行處理，再次執行VRkNN-Filter過濾算法，并將候選集進行合并，得到最終候選集；然后在候選集所在分區中執行VRkNN-Verification精煉算法，得到最終的并行反向k最近鄰查詢結果。算法SV_RkNN的數據流如圖3所示。

圖3 SV_RkNN的數據流

由圖3可知，SV_RkNN查詢處理算法包括Filter、Flatmap、Merge、Flatmap這4次轉換，其中Filter轉換可由全局網格索引定位查詢點縮小查詢范圍，從而縮小中間生成的RDD大小，接下來的Flatmap轉換完成過濾操作，產生窄依賴，而Merge轉換完成再次過濾操作，產生寬依賴，會發生數據的混洗，但此時數據經過過濾已經極大縮小當前的RDD，最后的Flatmap轉換完成精煉操作。此過程產生的中間RDD會在每次執行后刪除，但索引RDD仍駐留在內存中，重復使用的索引RDD可大幅度加速迭代的執行。

基于Spark并行反向k最近鄰查詢算法如算法4所示。

算法4： SV_RkNN

輸入： 網格索引GridIndex， Voronoi圖索引VoronoiIndexRdd， 查詢點集q， RkNN的k值;

輸出： 查詢集q的RkNN結果集合result;

begin

Grid_idArray←GridIndexQuery(q);

//查詢網格索引，確定查詢點q所在網格，將對應grid_id記錄在Grid_idArray中

VoronoiIndexRdd←

VoronoiIndexRdd.Filter(grid_id);

//根據Grid_idArray中的值確定相應局部索引

//過濾步驟

for the partition of VoronoiIndexRdd do

CandidateSetRDD←

VoronoiIndexRdd.flatmap(array?

VoronoiIndexRdd.VRkNN-Filter(P,qi,k));

Flag=0;

for each pointpin CandidateSetRDD do

ifpis in the neighboring partition do

flag=1;

partition←FINDPartition(P,p)

endif

endfor

endfor

if flag=1 do

for each partition do

CandidateSetRDD←

VoronoiIndexRdd.Flatmap(array?

VoronoiIndexRdd.VRkNN-Filter(P,q,k));

endfor

CandidateSetRDD.Merge();

endif

//精煉步驟

for the partition of CandidateSetRDD do

VerificationSetRDD←

CandidateSetRDD.Flatmap(array?

CandidateSetRDD.VRkNN-Verification (P,q,k));

result.Initialize;

result←VerificationSetRDD.reduce();

endfor

returnresult;

end

定理4 算法SV_RkNN的過濾步驟可以返回所有的結果(完備性)，且算法SV_RkNN的精煉步驟返回的結果是正確的(正確性)。

證明：(完備性)SV_RkNN算法的過濾步驟可以產生所有的候選。因為算法的過濾步驟分成兩個階段，第一個階段確定包含查詢點所在的分區，執行一次VRkNN-Filter過濾算法，過濾掉不可能成為候選的對象，根據定理3可知，過濾掉的對象不可能成為候選。第二個階段根據對象是否在其它的分區中，確定并行處理的分區，并再次進行VRkNN-Filter過濾處理，得到其它分區中的所有候選，并將所有候選合并為候選集，根據定理3可知，過濾掉的對象不可能成為候選，由此可知候選集中的對象包含了所有的結果，算法是完備的。

(正確性)SV_RkNN算法的精煉步驟不會刪掉真正的結果并且不會返回的不是實際RkNN的結果。首先，算法對候選集中對象所在分區進行處理，執行VRkNN-Verification精煉算法，對候選集中的所有對象進行處理，刪除錯誤的候選，根據定理3可知，刪除的候選是不可能成為真正的結果，保證了結果的正確性。可以利用反證法來證明結果集中不會返回不是實際RkNN的結果。假設結果集中返回的點p不是實際RkNN的結果，則p的kNN中一定不包含查詢點q，即p與q之間的距離一定大于p與其第k最近鄰之間的距離，而這樣的點在算法中一定會被刪除，不能成為結果，所以與假設相矛盾，由此證明結果集中不會返回不是實際RkNN的結果。證畢。

4 實驗結果及分析

實驗是在一個包含4個節點的Spark分布式集群上進行，它由1個master節點和3個worker節點組成，每臺機器的硬件配置都是：CPU型號為Intel CORE i5-104002.9 GHz六核處理器，內存為8 GB，硬盤1 TB。操作系統是64 位 Ubuntu16.04，Hadoop版本為2.7.1，JDK版本為1.7，Spark版本為2.0.1。

實驗中使用二維點數據來測試所提出的SV_RkNN算法，實驗數據來自于OpenStreetMap的3個數據集，這些數據集可以在SpatialHadoop官網[23]下載。數據集具體包括：Lakes、Parks和Roads。數據集詳情見表1。

表1 實驗數據集

實驗測試構建索引性能，實驗在不同分布數據集上分別比較本文創建索引算法GV-Index和文獻[2]中基于Map-Reduce的Voronoi-based算法(稱為MR_VD)的性能。

采用上述3個真實數據集進行實驗，對比GV-Index算法和MR_VD算法構建索引耗時，實驗結果如圖4所示。由圖4可知，對于每個數據集來說，GV-Index算法的構建索引耗時明顯少于MR_VD算法的耗時，這是因為Spark基于內存計算的特點，可以在內存中進行數據緩存，節省了時間。

圖4 數據集大小對索引構建耗時的影響

實驗測試算法總的執行時間，即算法響應時間。實驗在不同分布數據集上分別比較SV_RkNN算法和文獻[7]中基于LocationSpark的RkNN算法(稱為LS_RkNN)和文獻[7]中的基于Spatial Hadoop的RkNN算法(稱為SH_RkNN)的性能。

首先采用上述3個真實數據集進行實驗，取k=5，分析數據集規模對算法的查詢時間的影響。圖5給出了SV_RkNN算法、LS_RkNN算法和SH_RkNN算法的響應時間隨數據集大小的變化關系。由圖5可知，數據集的大小對3種算法的響應時間的影響不大，算法具有較好的穩定性。這是因為，兩種算法均采用了索引結構，而索引能夠使得數據的查詢范圍縮小在限定的范圍內，為此數據量的大小對響應時間的影響不大。但是，SV_RkNN算法的響應時間明顯少于LS_RkNN算法和SH_RkNN算法，這主要是因SV_RkNN方法進行RkNN查詢時，基于雙層索引結構，通過全局索引的過濾確定局部分區，可以避免訪問不必要的數據分區，只需在相關的數據分區內執行VRkNN查找，基于Voronoi圖的性質3，一個點的Voronoi近鄰最多為6，因此VRkNN中的kNN及每個候選點的第k個NN的查詢分別只需訪問6k個數據點，明顯縮短了響應時間，效果較好。

圖5 數據集大小對響應時間的影響

然后采用真實數據集Parks 和Roads進行實驗，分析k值的變化對SV_RkNN算法、LS_RkNN算法和SH_RkNN算法響應時間的影響。實驗選取k=1、5、10、15、20和30，實驗結果分別如圖6和圖7所示。由圖6和圖7可知，k值的變化對SV_RkNN算法和LS_RkNN算法的影響明顯小于k值的變化對LS_RkNN算法的影響。這是因為，隨著k值的增大，候選數量明顯增加，每一個分節點處理的數據量變大，SH_RkNN算法基于Spatial Hadoop，采取磁盤存儲策略，讀取大量的候選集需要多次的磁盤訪問，增加了輸入輸出操作的代價。而SV_RkNN算法和LS_RkNN算法基于Spark，采用基于內存計算的策略，減少了磁盤訪問的時間，查詢過程中使用的數據直接可用，因此相對于k值的增大而言相應的執行時間變化不大。而對比SV_RkNN算法和LS_RkNN算法，由于LS_RkNN需要執行KNN查詢(K遠大于k)，隨著k值的增大，候選數量明顯增加，而對于SV_RkNN算法，kNN及每個候選點的第k個NN的查詢訪問的數量分別為6k，因此隨著k值的增大，SV_RkNN算法的性能優于LS_RkNN算法。

圖6 Parks數據集k值變化對響應時間的影響

圖7 Roads數據集k值變化對響應時間的影響

最后采用真實數據集Parks進行實驗，取k=5，分析不同的計算節點數量對SV_RkNN算法、LS_RkNN算法和SH_RkNN算法響應時間的影響。實驗選取節點個數分別為1、2、3、4，實驗結果如圖8所示。由圖8可知，LS_RkNN算法的響應時間隨著節點個數的增加而減少，并且隨著節點數量越來越多，響應時間的減少幅度變小，這是因為節點數量的增加會增加節點之間的通信和調度時間，而且隨著節點數量的增加，響應時間的減小幅度逐漸降低。但是，隨著節點數量的增加，SV_RkNN算法和SH_RkNN算法的響應時間基本沒有改變，而SV_RkNN算法的性能優于SH_RkNN算法，這是因為，通過全局索引確定分區后，RkNN的查找只在確定的分區進行，也就是說，由查詢q的位置和k的值，可確定RkNN的查找通常在一個分區中進行，響應時間與節點的個數無關。

圖8 節點個數的變化對響應時間的影響

5 結束語

本文對基于Spark框架的并行反向k最近鄰查詢進行研究，基于Voronoi圖的良好特性，構建了基于網格-Voronoi圖的雙層索引機構，給出了索引構建算法，并在此索引結構上實現了基于Spark的并行反向k近鄰查詢，提出SV_RkNN算法，并通過真實數據集進行了實驗，將SV_RkNN與基于LocationSpark的RkNN算法和基于SpatialHadoop的RkNN算法進行了比較，實驗結果驗證了SV_RkNN相對比較算法具有更好的查詢性能和較好的穩定性。下一步計劃研究基于Spark框架的空間連接查詢，通過索引結構的改進，提高查詢的性能。