低滾動阻力轎車子午線輪胎帶束層設計優化

郭磊磊，胡德斌，崔志博，李 進，王 毅

（杭州海潮橡膠有限公司，浙江 杭州 310018）

隨著原油價格的不斷上漲，燃油經濟性已經成為運輸從業者最關心的問題之一。為幫助用戶提高運輸安全性、降低運營成本，降低輪胎滾動阻力是各輪胎公司的努力目標。輪胎滾動阻力的影響因素較多，橡膠的滯后損失是其主要來源。目前研究主要從輪胎結構、花紋和膠料配方3個方面來降低輪胎滾動阻力，提升整車的經濟性[1-5]。

本工作采用有限元仿真分析[6]，以205/55R16轎車子午線輪胎為研究對象，根據當前設計結構方案建立近似輪胎滾動阻力模型，研究帶束層角度、帶束層膨脹率和帶束層模量對輪胎滾動阻力的影響。

1 有限元模型及設計方案

1.1 材料模型

Mooney-Rivlin模型可用于橡膠材料的中、小變形研究，一般適用于應變大約為100%的拉伸應變和30%的壓縮應變情況，其表達式為

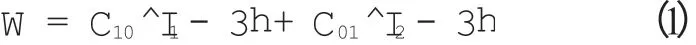
式中，W為應變能密度，C10和C01為橡膠材料常數，I1和I2為變形張量第一和第二不變量。

本工作通過單軸拉伸試驗確定橡膠材料的應力與應變關系，根據試驗參數擬合C10和C01。輪胎橡膠材料采用Mooney-Rivlin模型描述其力學性質，帶束層簾線、胎體簾線和冠帶層簾線等骨架材料采用線彈性材料進行描述[7-8]。

橡膠材料的粘彈性特征導致其變形時產生能量耗散，其損耗模量與儲能模量之比即為橡膠材料的損耗因子（tanδ）。使用VR-7120型動態力學分析（DMA）儀（日本UESHIMA公司產品）測試輪胎各部分橡膠材料60 ℃時的tanδ。

1.2 有限元模型

根據材料分布圖采用HyperMesh軟件的CGAX4H，CGAX3H，SFMGAX1單元完成輪胎斷面模型，其為帶縱向主溝的軸對稱結構，如圖1所示。采用Abaqus軟件的*SYMMETRIC MODEL GENERATION REVOLVE命令將輪胎斷面模型旋轉，生成完整的輪胎有限元模型[9]，如圖2所示。

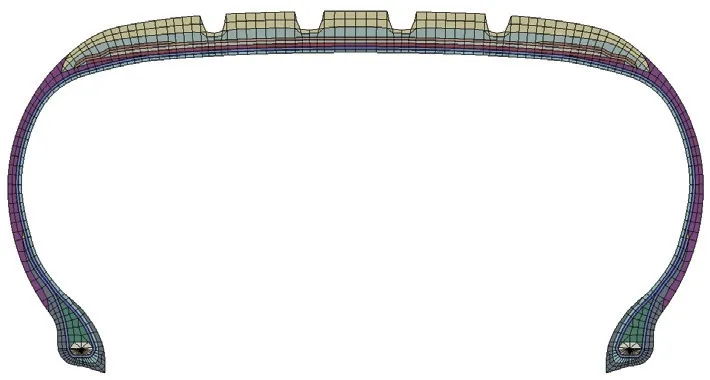
圖1 輪胎斷面有限元模型

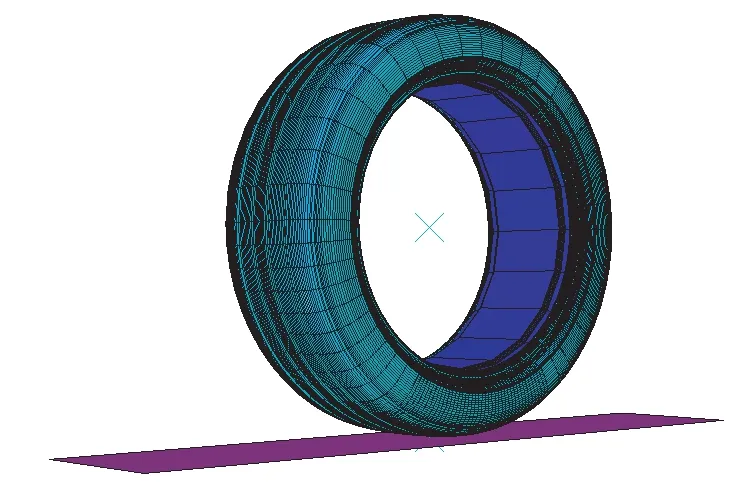
圖2 輪胎有限元模型

1.3 設計方案

選擇帶束層角度、帶束層膨脹率和帶束層模量3個設計因子，每個因子有8個水平，利用Isight軟件的試驗方法生成25個設計方案。

2 有限元模型驗證及輪胎滾動阻力的計算

2.1 有限元模型驗證

對205/55R16轎車子午線輪胎進行接地印痕、接地印痕矩形率、徑向剛度、橫向剛度和縱向剛度測試，試驗工況為：負荷 615 kg，充氣壓力 180 kPa，裝配輪輞 6.5J。

輪胎仿真和實測接地印痕分別如圖3和4所示，仿真與實測接地性能對比如表1所示。

圖3 輪胎仿真接地印痕

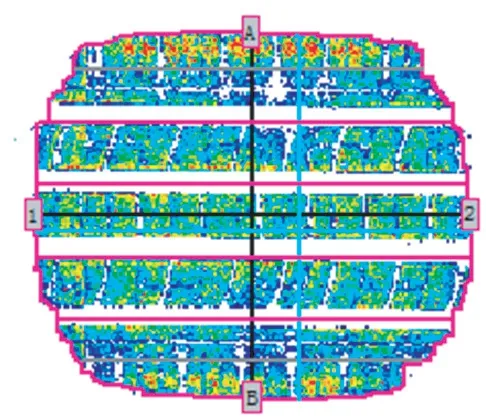
圖4 輪胎實測接地印痕

從圖3和4可以看出，輪胎仿真與實測接地印痕基本一致。從表1可以得出，輪胎仿真接地印痕矩形率、徑向剛度、橫向剛度和縱向剛度與實測結果的誤差分別為0.13%，0.98%，2.13%和2.71%，均小于5%。因此，本工作所建的輪胎有限元模型是準確的。

2.2 輪胎滾動阻力的計算

在諧應變情況下，輪胎材料在1個周期內的能量損耗（ΔW）為

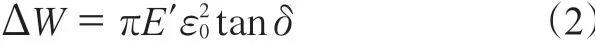
式中，E′為彈性模量，ε0為動態應變振幅。

則1個周期內輪胎的滾動能量損耗（EL）為

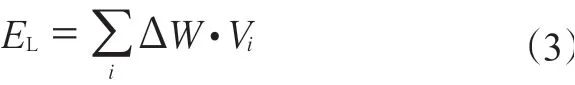
式中，Vi為輪胎各部分的體積，i為輪胎各部分的編號。

綜上可得[10]：

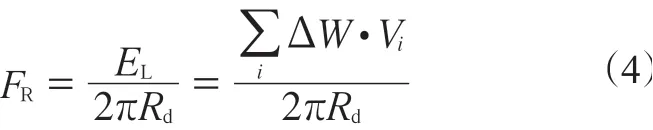
式中，FR為輪胎滾動阻力，Rd為輪胎滾動半徑。

仿真工況如下：負荷 492 kg，充氣壓力 210 kPa，裝配輪輞 6.5J，采用上述輪胎有限元模型可以得到不同方案的輪胎滾動阻力，如表2所示。

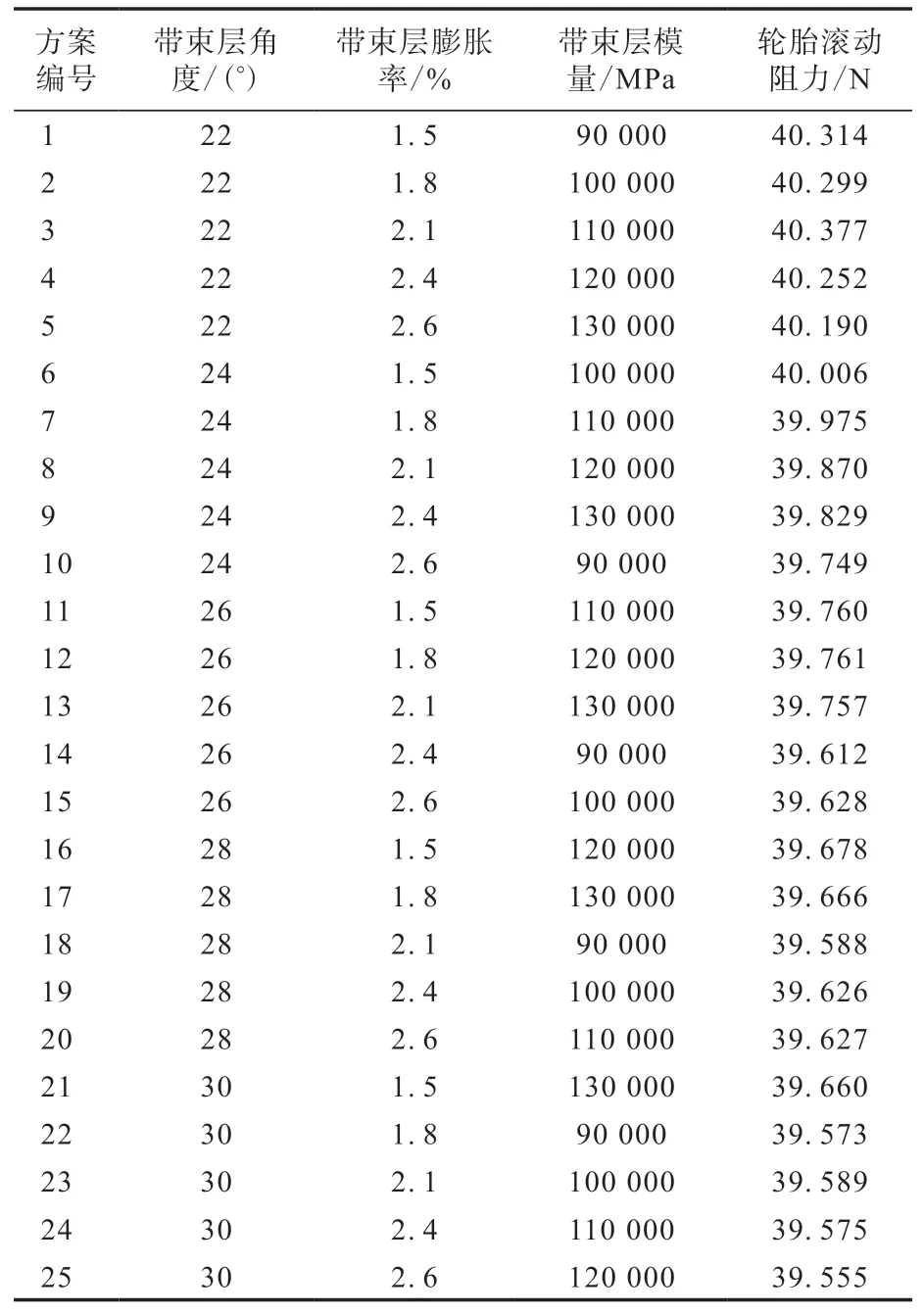
表2 不同設計方案的輪胎滾動阻力計算結果

3 結果與討論

3.1 各設計因子對輪胎滾動阻力的影響

利用Isight軟件對仿真數據進行分析[11]。帶束層角度、帶束層膨脹率和帶束層模量對輪胎滾動阻力影響的主效應分別如圖5—7所示。其中，設計因子對輪胎滾動阻力的主效應是因子在某個水平所有試驗中響應的平均值。

從圖5可以看出，輪胎滾動阻力隨著帶束層角度的增大而減小，且隨著帶束層角度逐漸增大，輪胎滾動阻力減小的趨勢也在減緩，帶束層角度對輪胎滾動阻力的貢獻率在79%左右。

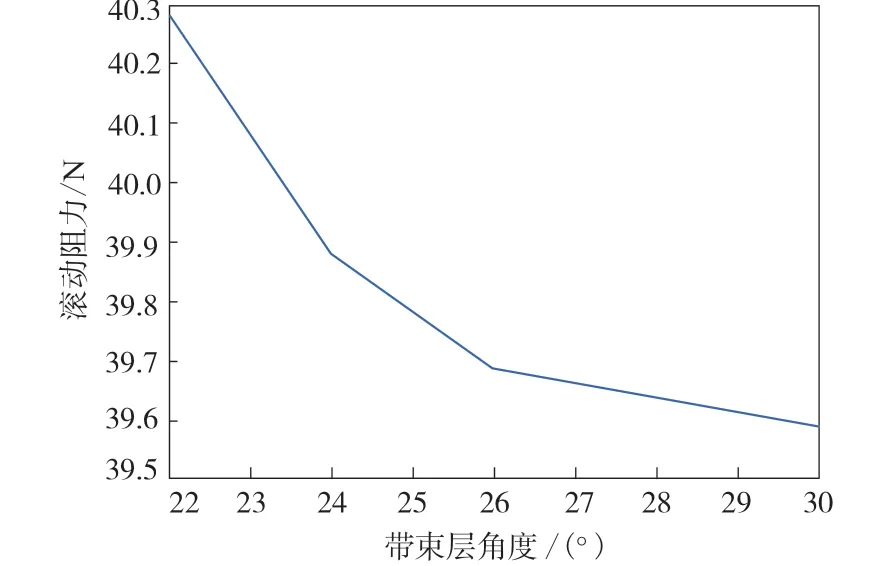
圖5 帶束層角度對輪胎滾動阻力影響的主效應

從圖6可以看出，輪胎滾動阻力隨著帶束層膨脹率的增大而減小，且隨著帶束層膨脹率的逐漸增大，輪胎滾動阻力減小的趨勢也在增大，帶束層膨脹率對輪胎滾動阻力的貢獻率在17%左右。

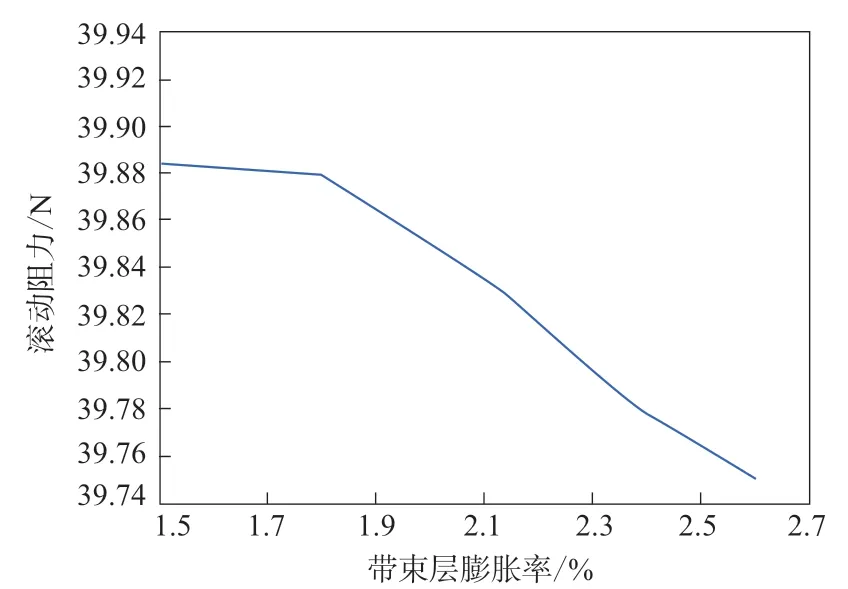
圖6 帶束層膨脹率對輪胎滾動阻力影響的主效應

從圖7可以看出，隨著帶束層模量的增大，輪胎滾動阻力先增大后減小，當帶束層模量為110 000 MPa時，輪胎滾動阻力最大，帶束層模量對輪胎滾動阻力的貢獻率不到5%。

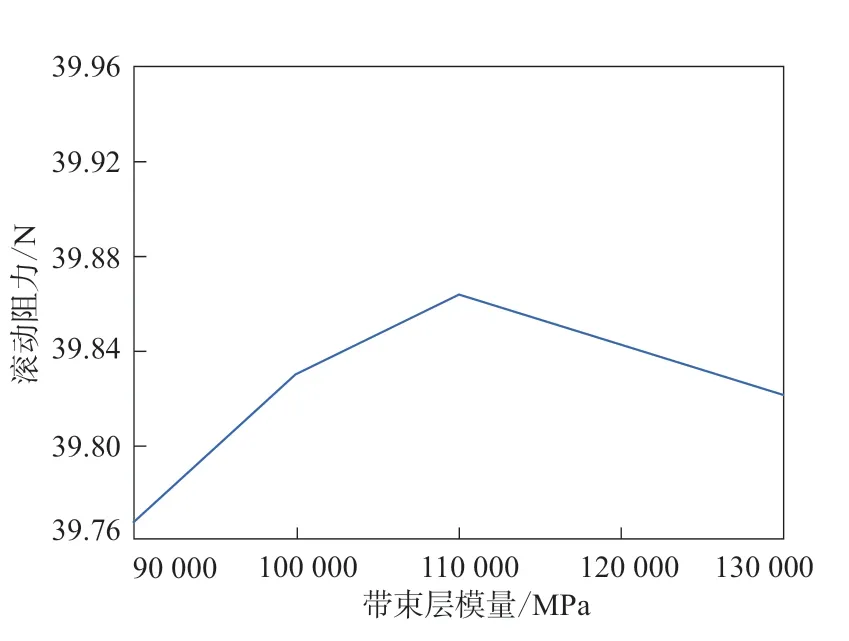
圖7 帶束層模量對輪胎滾動阻力影響的主效應

3.2 輪胎滾動阻力近似模型及其優化

近似模型法是通過數學模型逼近一組輸入變量（獨立變量）與輸出變量（響應變量）的方法[11]。本工作輪胎滾動阻力近似模型采用響應面方法和多項式函數擬合設計空間。為提高模型的精度和質量，以殘差平方和（SR）為最小目標，進行目標項的最佳選擇。SR計算公式如下：

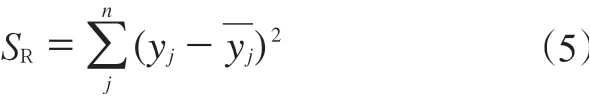
式中，yj為實際響應值，為擬合響應值，j為構造響應面模型的樣本點數，n為構造響應面模型的樣本點總數。

由于帶束層模量對輪胎滾動阻力的貢獻在5%以內，為提高模型的精度和質量，在建立近似模型時不考慮帶束層模量。

試驗方案選用4次響應面模型，得到輪胎滾動阻力近似模型如下：

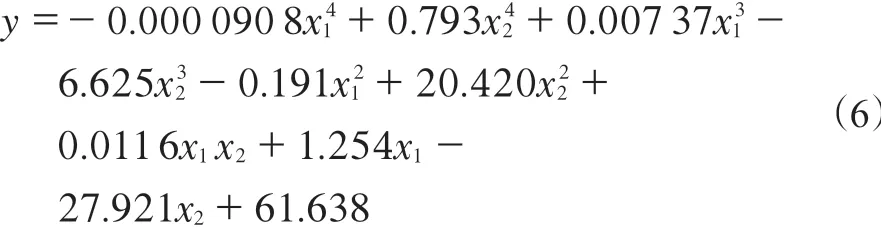
式中，y為輪胎滾動阻力，x1為帶束層角度，x2為帶束層膨脹率。模型擬合優度為0.995 1，可以認為輪胎滾動阻力近似模型和樣本點的符合度較高，近似模型具有較高的可信度。

利用Isight軟件對輪胎滾動阻力近似模型多項式進行優化，邊界條件為：帶束層角度 22°～30°，帶束層膨脹率 1.5%～3.0%，目標設置 輪胎滾動阻力最小。通過軟件計算后預測最優解為：帶束層角度 30°，帶束層膨脹率 2.55%，預測輪胎滾動阻力 39.456 N。

對上述最優解提供的結構參數進行輪胎滾動阻力仿真驗證，得到輪胎滾動阻力為39.472 N，與預測值誤差不到1%，該方案在25個方案中滾動阻力最小。

4 結論

（1）輪胎滾動阻力與帶束層角度和帶束層膨脹率負相關；隨著帶束層模量的增大，輪胎滾動阻力先快速增大后逐漸減小。通過主效應分析能夠仿真得出帶束層設計參數對輪胎滾動阻力的影響趨勢。

（2）帶束層角度對輪胎滾動阻力的貢獻最大，帶束層膨脹率次之，帶束層模量最小，在輪胎設計中可以通過調整帶束層角度來調整輪胎滾動阻力。

（3）對試驗數據建立近似模型再進行最優解分析能夠快速準確地獲得輪胎滾動阻力目標值，可代替高精度的有限元仿真模型進行輪胎優化設計，為低滾動阻力輪胎的優化設計提供了一種高效可行的方法。