基于實測數據的衛星公路運輸動力學特性仿真分析方法

王開浚，陳 夜，馬 超，張如變，彭海闊

（上海衛星工程研究所，上海 201109）

0 引言

衛星研制完成后一般會通過公路、鐵路或航空等途徑運輸至發射場，其中公路運輸環境相比鐵路及航空運輸環境更加復雜：由于道路不平，導致大量隨機載荷通過運輸車輛傳遞至衛星包裝箱，所誘發的振動、沖擊傳遞至衛星結構，易對衛星造成不利影響甚至導致衛星結構局部損傷[1]。有學者針對航天器公路運輸進行了研究。O’Connel 根據實際數據修正了運輸動態數據庫以及美國NASA 噴氣推進實驗室的運輸標準和運送方法[2]。何柏巖等采用車輪力傳感器和加速度計測量了道路行駛中的載荷譜，并對力信號和加速度信號進行了功率譜密度分析，得到中國部分道路行駛載荷的累積幅值頻次圖[3]。師立俠等對航天器在公路運輸過程中動力學環境的誘因和特點進行了研究，明確路面不平和車輛突然加減速是誘發振動、沖擊的主要因素[4]。田千里等優化分析了在隨機路面上行駛時使包裝箱響應最小的鋼絲繩隔振器參數，提出了統計線性化分析方法；該研究將衛星與車輛簡化為二自由度體系，無法對衛星結構受力情況進行描述[5]。為保證衛星公路運輸過程的安全可靠，目前通常須在運輸前進行跑車試驗[6]，但跑車試驗需要消耗較多人力、物力和時間，無法滿足當下日趨密集的衛星發射對研制成本和進度的要求。

衛星結構的動力學特性分析方法主要包括數學解析法、試驗法和有限元仿真法。有限元仿真法因其成本低、精度高、可修正性強等優點目前被廣泛應用。本文對近6 年來數十個不同平臺的衛星公路運輸實測時域數據進行處理，得到運輸過程載荷輸入譜；利用有限元軟件Patran/Nastran 建立包裝箱-衛星聯合仿真模型，對衛星運輸過程中的動力學特性進行分析并得出衛星各部位最大的加速度及應力響應結果。該結果可作為衛星公路運輸過程可靠性及安全性的評判依據，以替代原先的跑車試驗；在提高研制進度和節約研制成本的同時，可為后續衛星及包裝箱設計提供依據。

1 公路運輸實測數據處理方法

圖1 為一典型衛星公路運輸過程中的實測時域響應曲線。可以看出，衛星在運輸過程中所經受的力學環境主要為隨機振動。對于時間歷程明顯是非周期性函數的隨機振動，可用功率譜密度（PSD）函數反映隨機過程的頻域特征。功率譜密度函數給出了某一過程的功率（均方值）在頻域的分布規律，可以判別各種頻率成分能量的強弱。

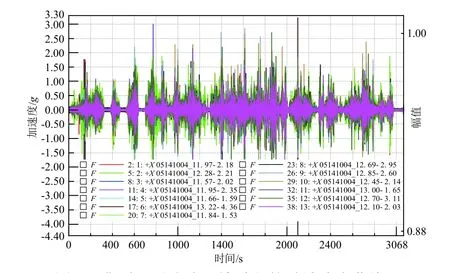
圖1 典型衛星公路運輸過程的時域響應曲線Fig. 1 Time domain response curve of a typical satellite in road transport process

對于平穩隨機過程，其自相關函數與功率譜密度互為傅里葉變換[7]：

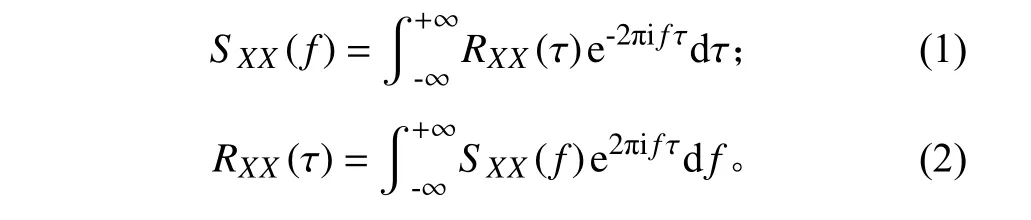
其中：SXX(f)是函數x(t)的功率譜密度；RXX(τ)是自相關函數。

根據傅里葉變換，自相關函數RXX(τ)是絕對可積的，當τ=0 時，有

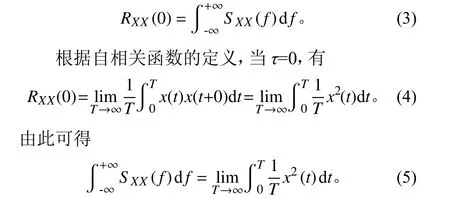
由式(5)可知，SXX(f)曲線下的總面積與x2(t)/T曲線下的總面積相等。

從物理意義上講，x2(t)是隨機信號x(t)的能量，而x2(t)/T則是隨機信號x(t)的功率。因此信號x(t)的總功率為

這一總功率與SXX(f)曲線下的總面積相等，因此SXX(f)曲線下的總面積就是信號的總功率。它是由無數不同的功率元SXX(f)df組成，其大小反映了總功率在不同頻率處的功率分布。

衛星在運輸過程中其3 個方向的隨機振動譜圖和量值均不相同。以縱向為例，基于歷次衛星運輸的實測時域數據，利用LMS 分析軟件將時域數據轉化為加速度譜密度曲線（見圖2(a)），從而得到具有安全余量的仿真分析輸入譜最大包絡曲線（見圖2(b)）。

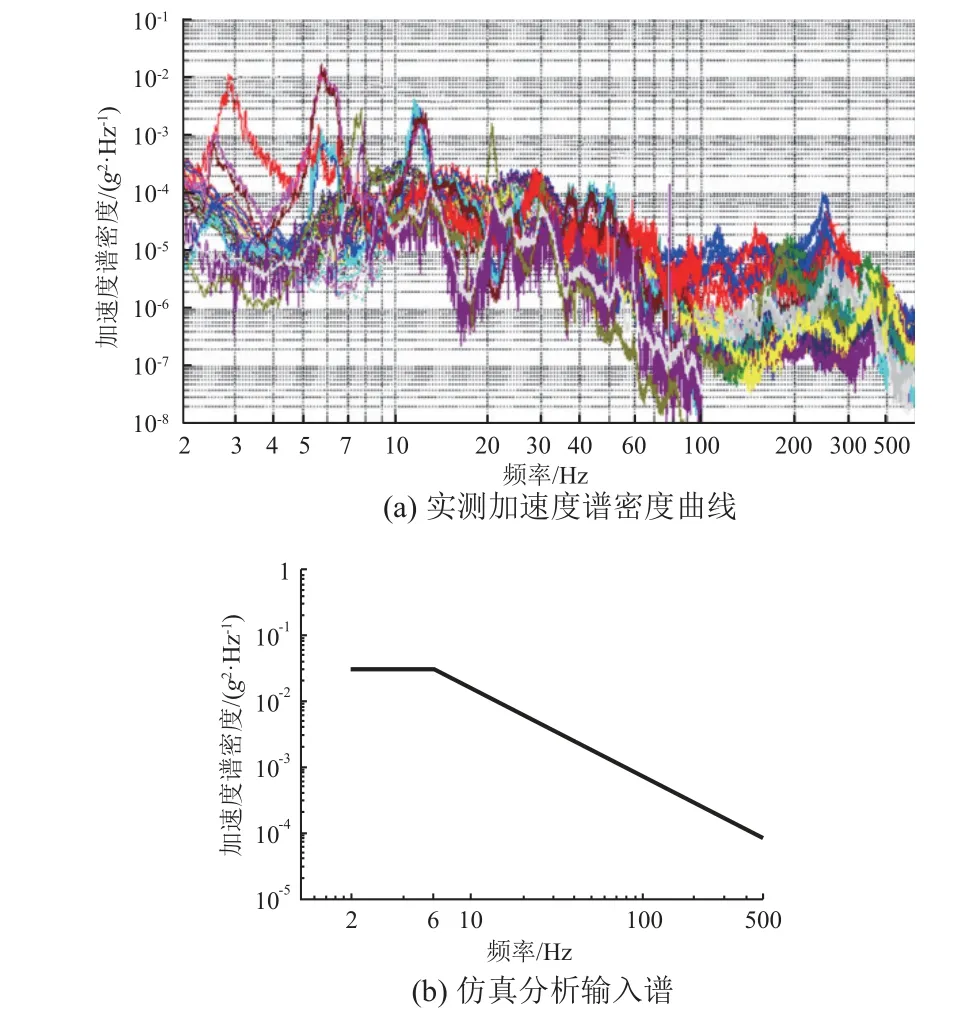
圖2 歷次衛星運輸的實測加速度譜密度曲線和仿真分析輸入譜（縱向）Fig. 2 Measured PSD (a) and its envelope (b) of satellite by ground transportation (longitudinal)

2 仿真模型建立

以某衛星為對象，建立了包裝箱和衛星的聯合仿真模型。考慮到箱體、減震器、L 梁和衛星的剛度特性，模型以減震器下端為輸入界面，箱蓋不參與建模，主要對減震器-L 梁-衛星進行詳細聯合分析；衛星以殼單元等效為主，包裝箱以體單元等效為主，減震器等效為Bush 單元。仿真模型的總節點數為53 730 個，單元數為53 603 個。衛星模型選取根據力學試驗修正后的，組合體模型則通過組合體模態試驗結果進行修正，以確保仿真模型的準確性。力學分析模型如圖3 所示。

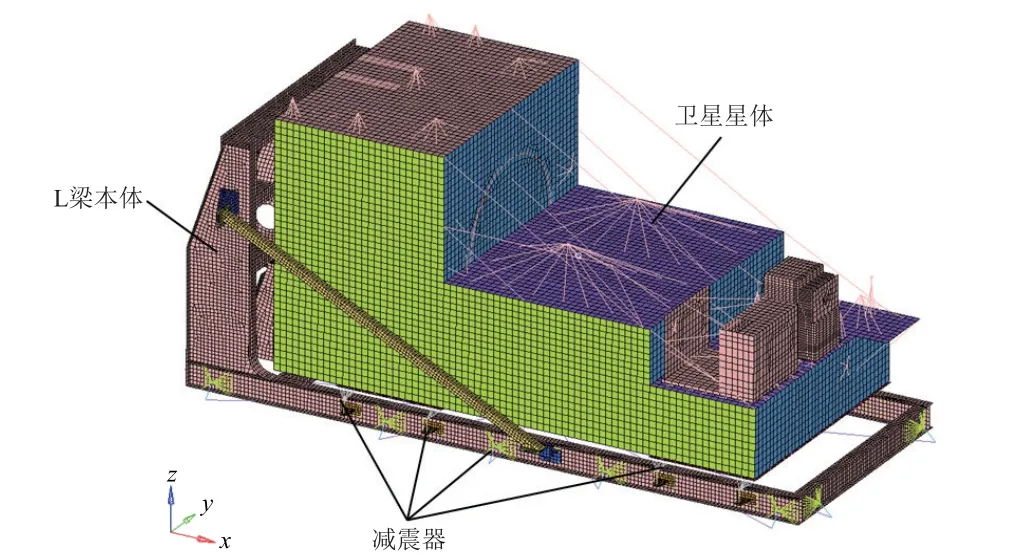
圖3 考慮L 梁和減震器的衛星公路運輸有限元模型Fig. 3 FEM of satellite with L beam and shock absorbers for vehicle in road transportation

衛星質量為2800 kg，采用平躺方式通過工藝鋁合金側板與L 梁連接；L 梁下端采用減震器固連在包裝箱上。減震器的關鍵部件為鋼絲繩彈簧，故仿真模型將該減震器等效為彈簧單元，在局部坐標系下建立連接關系并定義彈簧剛度和阻尼系數，其連接形式和等效示意如圖4 所示。通過靜、動剛度及阻尼試驗獲取鋼絲繩彈簧的力學參數，最終得到仿真模型中鋼絲繩彈簧的等效彈性模量為1.05×109Pa，材料阻尼系數為1.125×106N·s·m-1。

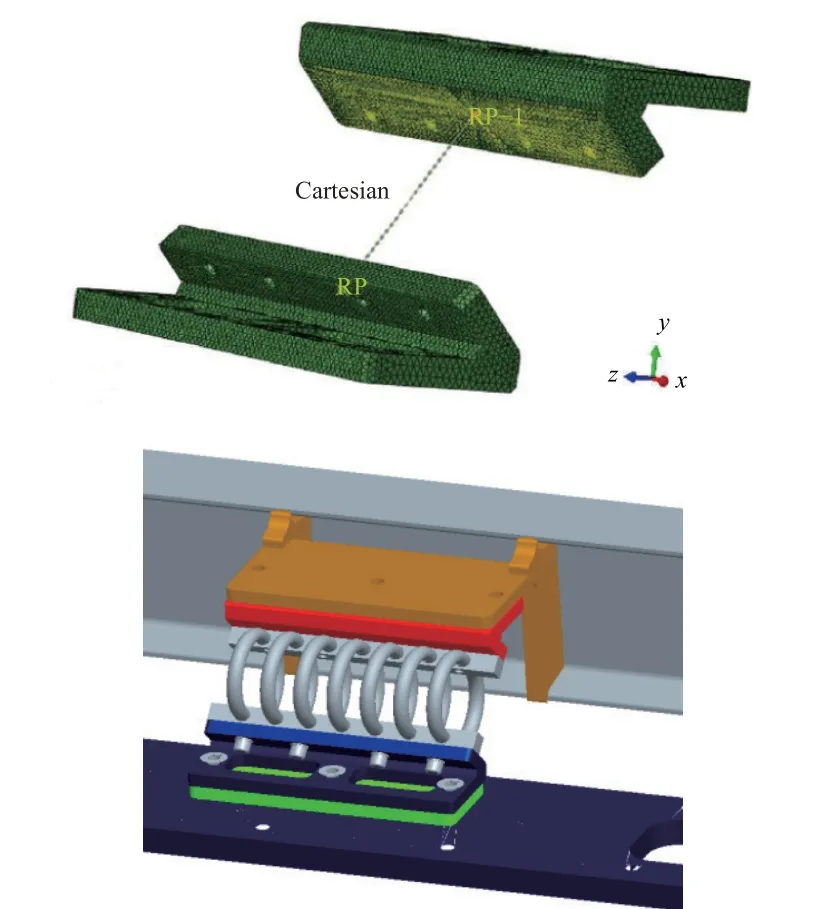
圖4 鋼絲繩彈簧連接關系模型Fig. 4 FEM for connection relation of wire rope spring

3 模態分析

根據組合體模態試驗結果對仿真模型進行修正，再對修正后的聯合仿真模型進行模態分析，約束條件為減震器下端固支。提取前6 階固有頻率和振型，得到模態分析值見表1，所對應的彎曲振型見圖5。

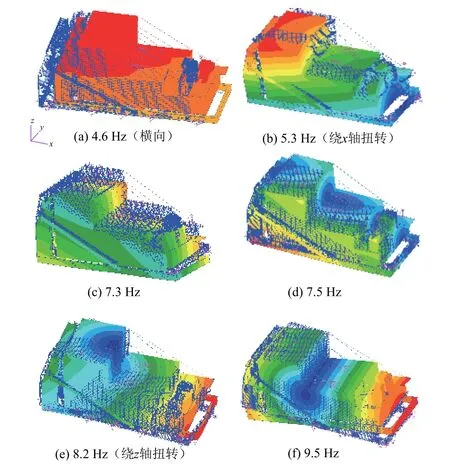
圖5 衛星和包裝箱的聯合有限元模型各階模態振型Fig. 5 Modal shapes of finite element model of the satellite and its packaging box

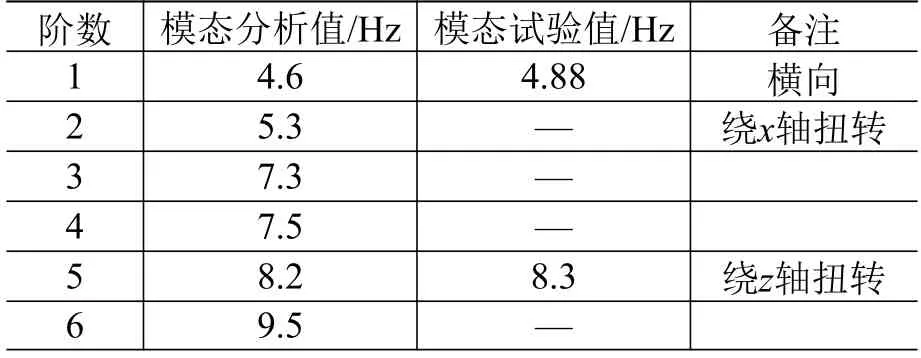
表1 衛星和包裝箱的聯合有限元模型模態分析值Table 1 Modal analysis results of finite element model of the satellite and its packaging box

4 隨機振動響應分析

4.1 分析方法

將衛星平穩運輸過程載荷譜數據作為輸入條件，分析平穩行駛狀態下包裝箱-衛星聯合模型的結構應力情況。在有限元軟件中將隨機振動分析當作頻率響應分析的后處理來進行：輸入文件包括頻率響應分析的輸出結果和PSD 函數，PSD 的響應類型可以是位移、速度、加速度、應力或壓力等，代表外界激勵；輸出結果為響應的PSD 和RMS 值。隨機響應分析流程見圖6。

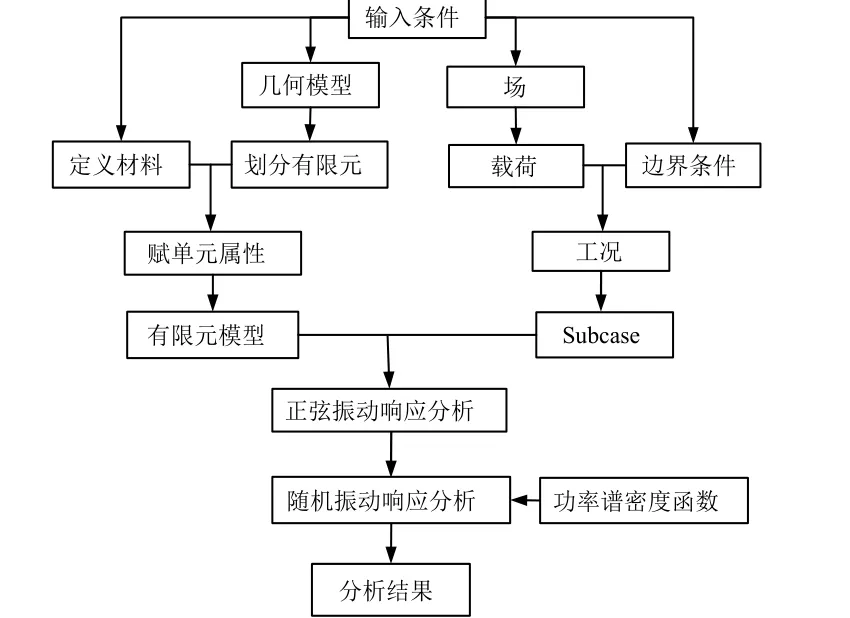
圖6 隨機振動響應分析流程Fig. 6 Flowchart for random vibration response analysis

4.2 分析結果

根據上述仿真分析方法，對不同頻率范圍（5～150 Hz）內模型關鍵部位的隨機振動響應進行了計算。結果表明：響應、應力較大區域均位于L 梁及L 梁與衛星連接的側板處。提取連接側板、L 梁支撐板的應力和加速度均方根（RMS）結果，分別如圖7 和圖8 所示。

由圖7 和圖8 可知，在實際運輸過程中隨機加速度條件下，衛星與L 梁連接側板的最大應力RMS值為17 MPa，對應3σ應力為51 MPa；L 梁支撐板的最大應力RMS 值為63.7 MPa，對應3σ應力為191 MPa，遠小于鋁合金材料的屈服極限270 MPa。分析結果表明，隨機振動對包裝箱-衛星模型的影響有限，即衛星結構具有足夠的安全裕度。

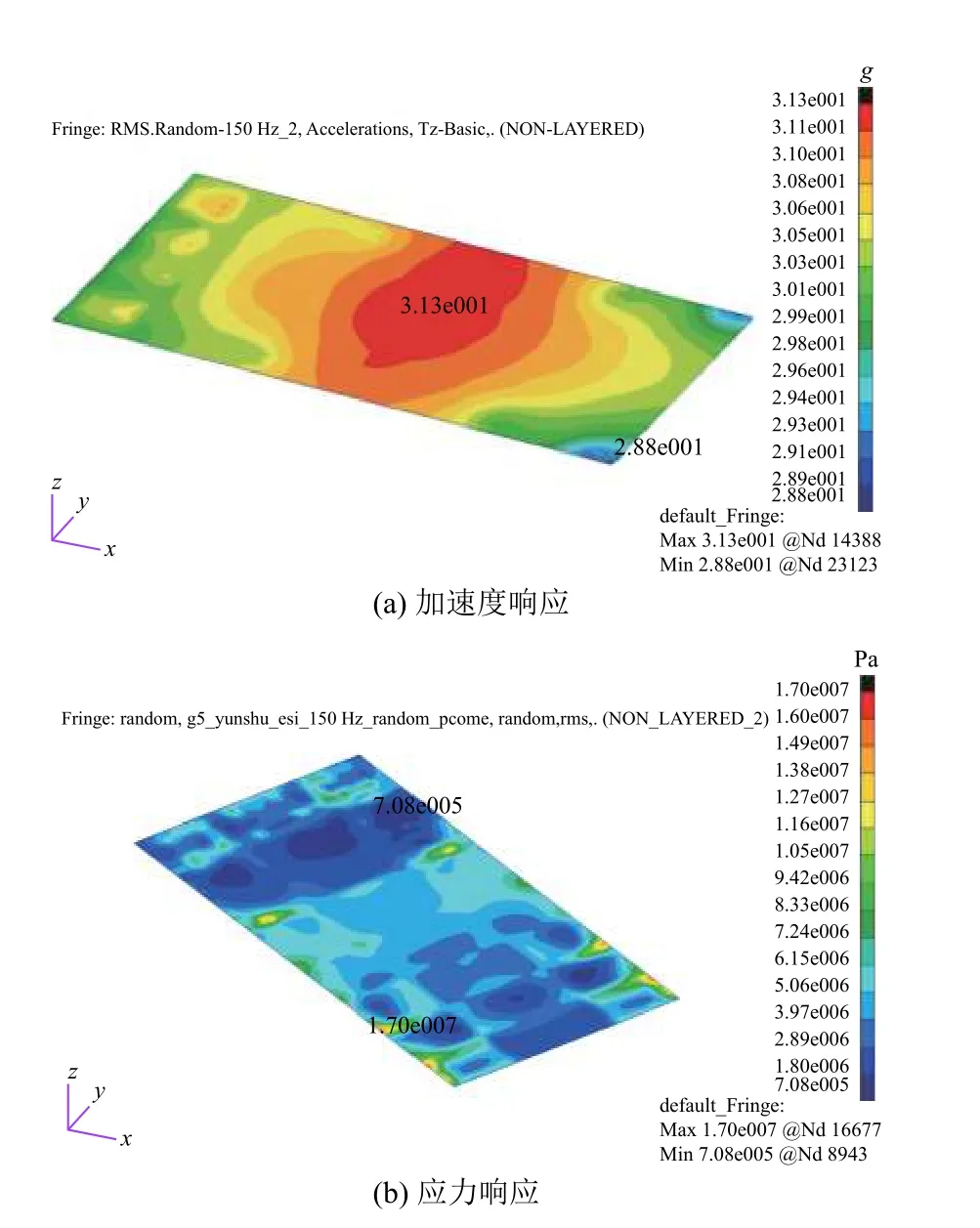
圖7 連接側板的加速度和應力RMS 云圖Fig. 7 RMS of acceleration and stress responses of the side panel

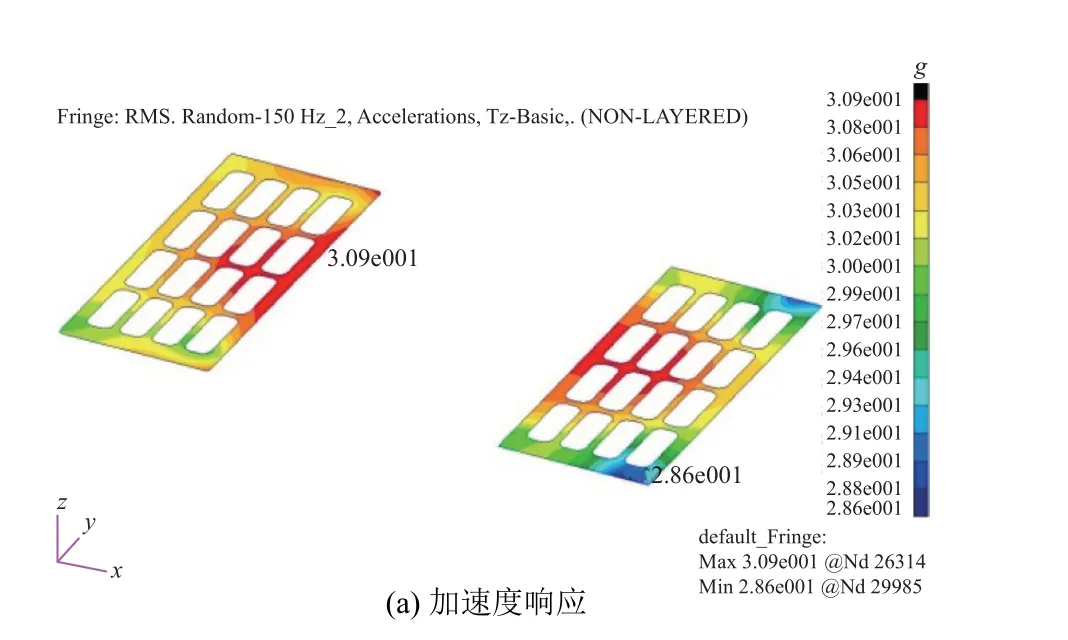
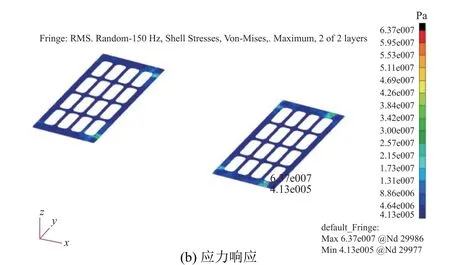
圖8 L 梁支撐板的加速度和應力RMS 云圖Fig. 8 RMS of acceleration and stress responses of the mounting plate of L beam

對比不同頻率范圍下的分析結果如表2 所示。可以看出，隨機振動分析時，在分析頻率大于15 Hz的頻段，衛星連接側板和L 梁結構的應力和加速度RMS 值均未變化。故在隨機響應分析時，高頻振動對結構應力和加速度的影響可以忽略。因此考慮衛星公路運輸過程隨機振動對結構的影響時，分析頻段可不超過50～100 Hz。

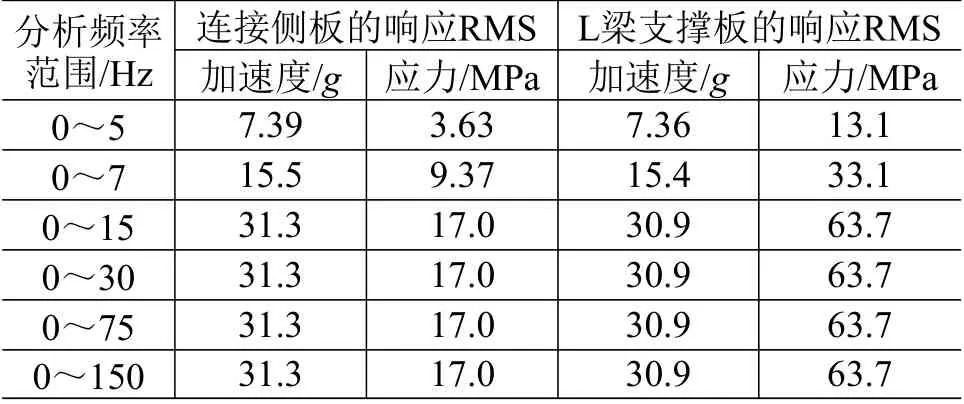
表2 不同頻率范圍下的隨機振動分析結果Table 2 Results of random vibration analysis for different copes of frequency

5 結束語

衛星在公路運輸中所經受的載荷主要表現為隨機振動。通過對包裝箱-衛星組合的有限元模型動力學特性分析，得到了模型的前6 階模態振型，并在模態分析的基礎上得到了包裝箱及衛星關鍵部位的加速度及應力響應。結果表明：

1）隨機振動通過包裝箱作用于衛星主結構上的加速度及應力很小，對衛星的動態力學性能影響有限，衛星結構具有較高的安全裕度；

2）隨機振動應力較大區域一般位于衛星與L 梁連接處，因此可以考慮采用工藝側板替代正式產品參加運輸，以提高整星的安全性；

3）衛星運輸過程中主要受低頻振動影響，故仿真分析頻段可不超過50～100 Hz。