永磁同步電機電流的無差拍自抗擾控制

張本翔，左月飛，全 力，朱孝勇

（江蘇大學電氣信息工程學院，江蘇鎮江 212013）

0 引言

永磁同步電機以其高功率、高密度和高效率等特點被廣泛應用于工業伺服系統中，例如機器人機械臂、數控機床、紡織機械、煤礦生產等領域。永磁伺服系統通常由位置環、轉速環和電流環組成，其中作為內環的電流環對整個伺服系統的性能起著決定性作用。

電流環一般采用PI 控制［1］，但控制系統存在的延時限制了其動態性能的提升［2］，而且由于積分器可能造成積分飽和［3］，導致超調過大、整定時間增加，無法滿足快速運動場合的需求。為進一步提高電機的動態響應能力，有學者提出了模型預測控制［4］和無差拍預測控制［5］。模型預測是利用代價函數計算7 種電壓矢量后得到最優解［6］，但開關頻率不固定［7］，電流存在抖動。相比于模型預測控制，無差拍控制利用空間矢量脈寬調制技術［8］，開關頻率固定，可獲得更平滑、準確的電流波形，但采用無差拍預測控制的前提是模型參數必須精確。由于在電機運行過程中，溫度變化和磁飽和有可能導致電機參數發生變化，該方法便不再適用［9］，因此提高系統參數的魯棒性至關重要。

文獻［10］在無差拍控制中引入自適應增量算法，減少了電機參數失配帶來的不利影響，但是受電感的影響，電流存在較大脈動；文獻［11］提出一種魯棒因子并將其加入無差拍控制中，能夠在電感變化時提高系統的穩定裕度，但是該方法是以犧牲系統的動態性能為代價的；文獻［12］將參數辨識與無差拍相結合，對電機的電感和電阻進行辨識，有效提升了系統的動態性能和參數魯棒性，不過并未考慮對磁鏈的辨識。文獻［13］指出，在無差拍預測控制中，電機的磁鏈失配會導致電流跟蹤存在穩態誤差。為此，文獻［14］分析了電機參數不匹配對傳統無差拍預測控制的影響，并將滑模控制與無差拍預測控制相結合，設計了滑模觀測器估計擾動，使參數具有較好的魯棒性，然而滑模控制下的電流存在抖振現象。為降低系統抖振水平，文獻［15］基于無差拍控制設計了快速功率滑模趨近律，文獻［16］在滑模中采用二階趨近律，均有效降低了抖振，但在控制器的參數整定上較為繁瑣。相比于滑模觀測器，自抗擾控制中的擴張狀態觀測器也可對參數變化引起的擾動進行觀測，而且不存在滑模控制固有的抖振問題［17］。文獻［18］將無差拍控制與擴張狀態觀測器相結合用于異步電機中，取得了較好的控制效果。文獻［19］、［20］在無差拍控制中引入無模型算法，但該方法將已知量看作擾動，容易使觀測誤差過大，導致系統的控制性能降低。

本文借鑒自抗擾控制思想，首先針對無差拍電流控制易受電機參數變化而產生擾動的問題，提出利用擴張狀態觀測器估計參數擾動并實時進行補償，同時針對延時問題，利用擴張狀態觀測器對電流和擾動進行預測，實現了無差拍電流預測控制。其次，本文從理論上分析了噪聲對觀測器帶寬的影響，平衡了帶寬與噪聲之間的關系，實現了快速的電流跟蹤響應，增強了系統魯棒性且參數整定方便。最后的實驗結果證實了本文方法的有效性。

1 電流自抗擾控制器設計

1.1 PMSM數學模型

永磁同步電機在轉子磁場定向的同步旋轉坐標系（dq坐標系）下的電壓方程為：

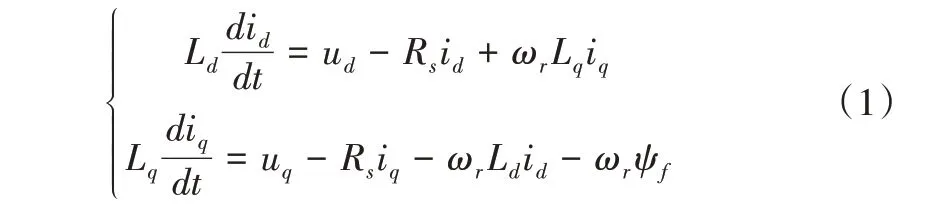
式中，id和iq、ud和uq、Ld和Lq分別為d-q坐標系下的電流（A）、電壓（V）、電感（H），Rs為定子電阻（Ω），ωr為轉子電角速度（rad/s），ψf為永磁磁鏈的幅值（Wb）。

將電流狀態方程表示為復矢量fdq=fd+jfq的形式：

式中，udq1=udq-jωrψf為電壓，a=-（Rs/Ldq+jωr）為狀態系數，b=1/Ldq為電流控制增益。

在實際的電機控制系統中，與電機參數相關的a、b可能是未知或時變的，通常采用其估計值來代替。當估計值與實際值存在偏差時，系統中就會產生擾動電壓。另外，由于逆變器的死區時間和功率器件的壓降會導致期望電壓與實際電壓不相等，也會產生相應的擾動電壓。因此，需要將電流狀態方程修改為：

式中，為期望的電壓，也即電壓給定值，d為參數不確定性和電壓誤差等因素導致的擾動。

1.2 反饋控制律設計

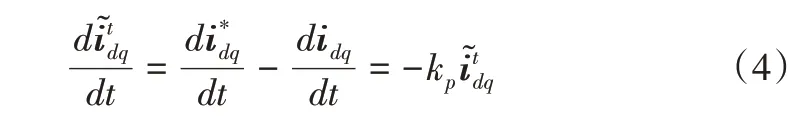
式中，kp為反饋控制增益。

將式（3）代入式（4），并忽略電流給定的微分項可得到：

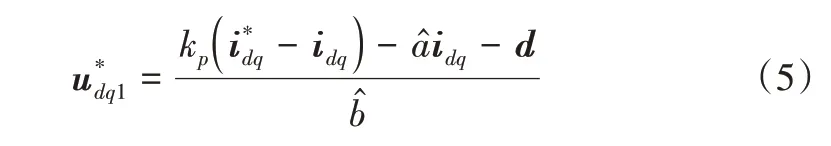
式（5）中的電流idq通常由霍爾電流傳感器測量得到，因此測量值中會存在測量噪聲。假設測量值與測量噪聲分別為另外，擾動d為未知量，難以直接通過測量獲得。為減小噪聲并實現擾動補償，通常采用觀測器對電流和擾動同時進行估計，并用其估計值代替實際值。不妨假設電流與擾動的估計值分別為則電壓給定值為：

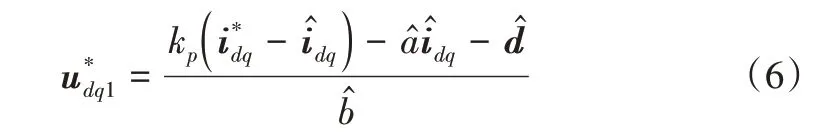
考慮到實際系統中PWM 占空比最大為1，常采用飽和函數對電壓進行限幅：

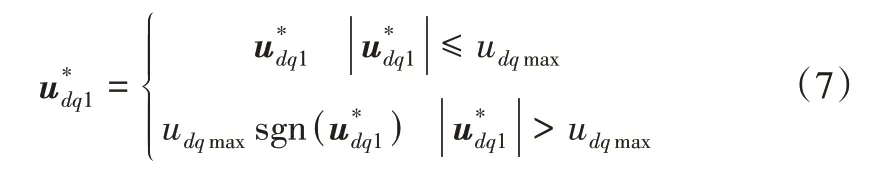
式中，udqmax為電壓的限幅值。

在自抗擾控制系統中，通常采用擴張狀態觀測器（Extended State Observer，ESO）同時觀測狀態和擾動，以下對ESO 進行設計與分析。

1.3 電流與擾動估計

對式（3）表示的系統構建ESO 狀態方程為：

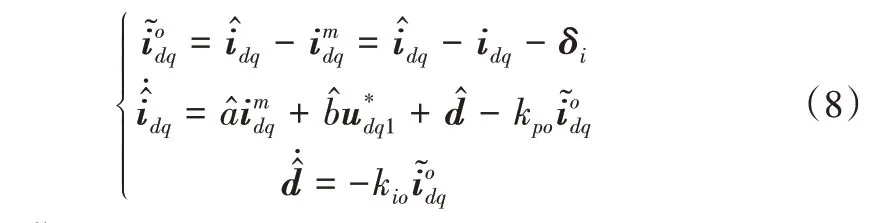
由式（8）可得電流觀測誤差、電流估計值和擾動估計值分別為：

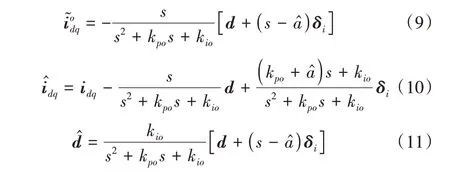
由式（10）可看出，系統沒有擾動時，ESO 能夠實現對真實電流的完全跟蹤，且能夠抑制測量噪聲。由式（11）可看出，在不考慮測量噪聲的情況下，估計的擾動是對實際擾動的二階低通濾波。設定ESO 系統的特征方程為s2+，其中ωn為無阻尼自然頻率，則kpo=2ωn，kio=越大，ESO 對擾動的估計越快，擾動補償后系統的抗擾性能越強，但系統的噪聲也會越大，將導致系統的控制性能下降。因此，實際系統中應根據具體情況對ωn進行調節。

1.4 自抗擾控制系統性能分析

根據式（6）、式（8）可繪制出電流自抗擾控制系統的結構框圖，如圖1所示。

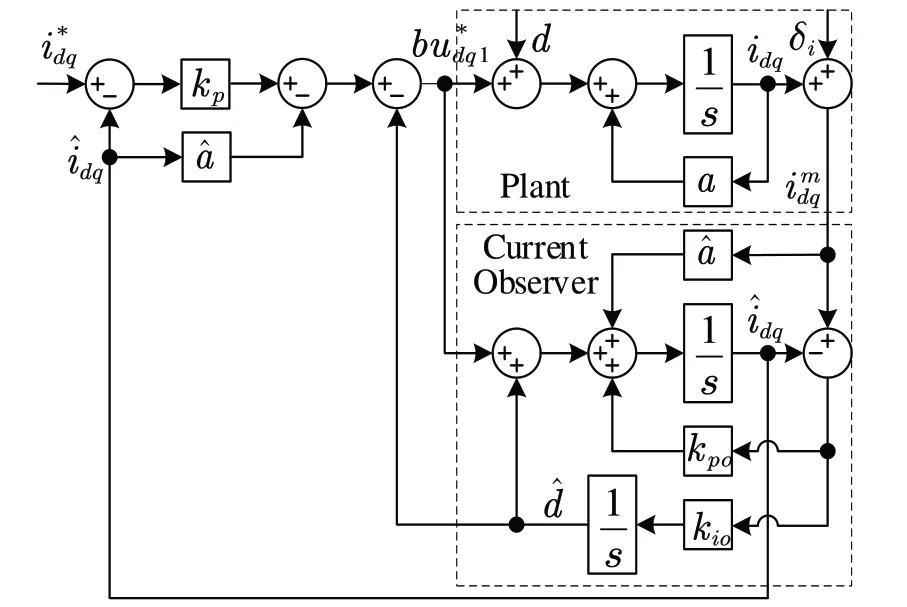
Fig.1 Block diagram of the ADRC current control system圖1 電流自抗擾控制系統結構框圖

給定電流、擾動和噪聲到輸出電流的傳遞函數分別為：

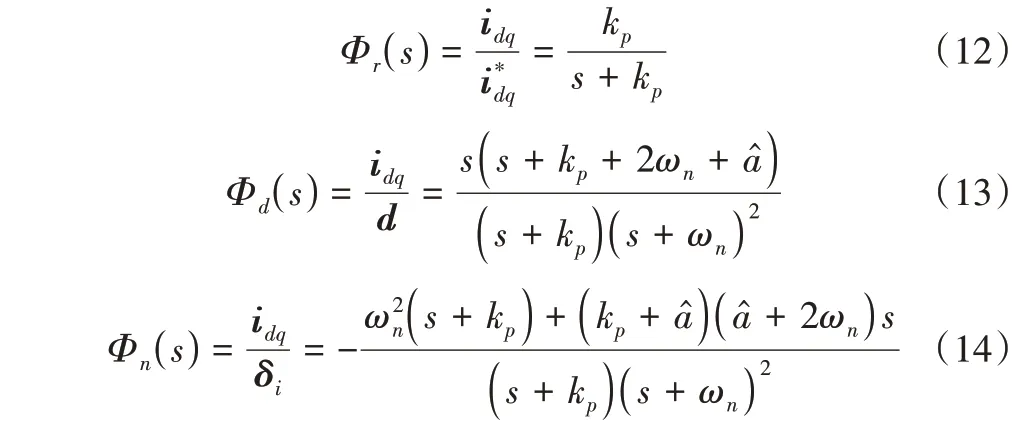
為更直觀地看出調節無阻尼自然頻率ωn對擾動和噪聲的影響，根據式（13）、式（14）分別繪制了相應的頻域特性圖，如圖2、圖3所示（彩圖掃OSID 碼可見，下同）。

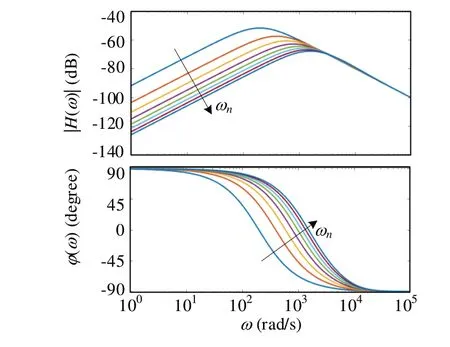
Fig.2 Frequency domain characteristics of disturbance to output current圖2 擾動到輸出電流的頻域特性

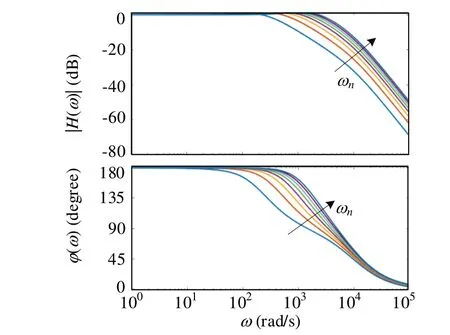
Fig.3 Frequency domain characteristics of measured noise to output current圖3 測量噪聲到輸出電流的頻域特性

由圖2 可以看出，隨著ωn的增大（箭頭所指方向），系統抗低頻擾動的幅值減小；隨著ωn的減小，系統抗低頻擾動的幅值增大，因此從抗擾能力方面考慮，ωn應越大越好。由圖3 可以看出，隨著ωn的增大，系統抑制高頻噪聲的幅值增大，但隨著ωn的減小，在高頻部分反而有利于抑制高頻噪聲幅值，因此從抑制噪聲能力方面考慮，系統的ωn應越小越好。然而，由于ωn與系統的抗擾能力有關，在實際中需要平衡好擾動觀測與噪聲抑制的關系。

由于電流環是內環，電流環的跟蹤性能處于更重要的位置，因此應先設定較大的kp以獲得較好的跟蹤性能，之后再根據噪聲情況盡量增大ωn以提高觀測器的動態性能，從而增強系統的抗擾性能。在實際系統中，由于kp較大，通常ωn會較小，因此系統對快速變化的擾動抑制性能較弱。為提高系統的控制性能，應盡量提高電機參數的準確性，并減小其它因素造成的擾動。

2 無差拍電流預測自抗擾控制器

2.1 傳統無差拍電流控制與分析

為獲得更好的電流動態響應能力，本文采用無差拍控制方法。無差拍電流控制是基于離散化的控制方法，考慮到采樣時間Ts較小，因此可采用前向歐拉法將式（2）離散化得：

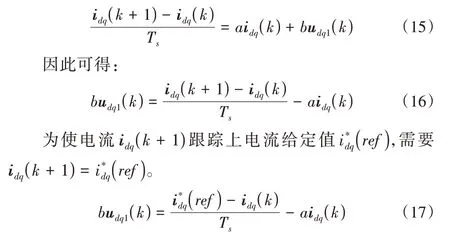
但是式（17）所表示的傳統無差拍電流控制方法并未考慮到數字控制系統中的一步延時問題，如圖4所示。

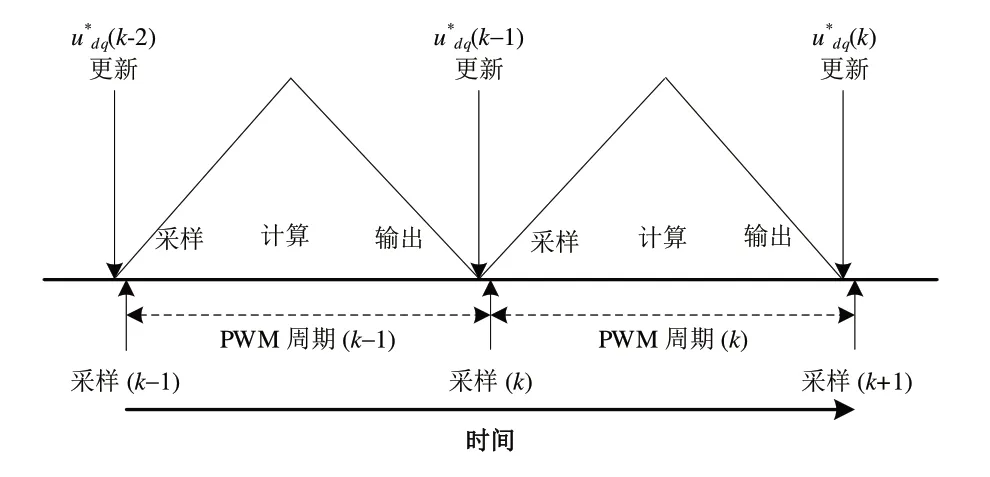
Fig.4 One step delay of digital control system圖4 數字控制系統的一步延時

在PWM 觸發后，施加到電機上的電壓并非為本周期的控制量，而是上一周期計算所得，因此會產生一步延時。延時問題會降低系統的動態性能，因此針對這一問題，普遍采用延時補償進行消除，于是得到：

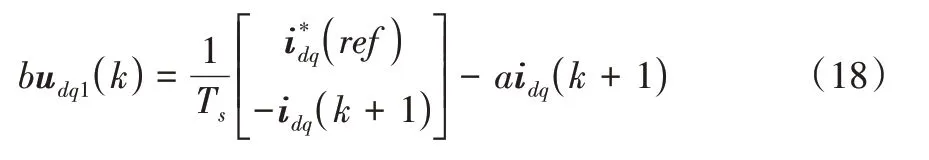
為推導電機參數變化對傳統無差拍電流預測控制造成的影響，以q軸為例，采用電機參數的估計值，由式（18）可得出：

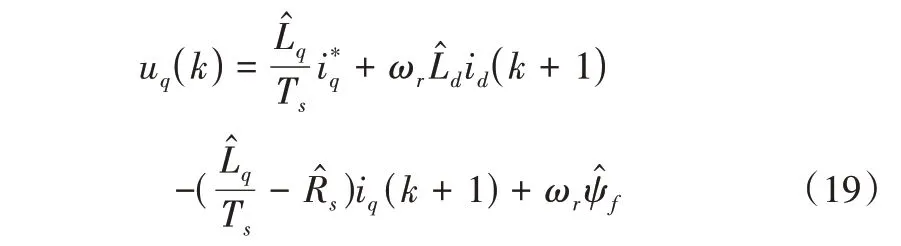
考慮延時補償，將式（15）轉換為：

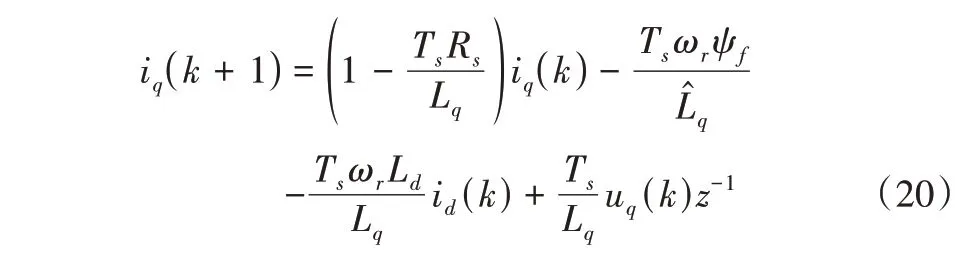
將式（20）代入式（19），整理得到：

如果采用id=0 的控制方式，不計d軸電流，忽略電阻和磁鏈的影響，可得：

由式（21）可得出，在電機參數匹配時，反饋電流在穩態時可實現無誤差地跟蹤；在電感和電阻參數準確時，磁鏈失配會產生電流跟蹤穩態誤差。由式（22）的特征方程可知 其特征根為于 是可解得說明在傳統無差拍預測控制中，如果估計電感大于2 倍的實際電感，系統則會不穩定，因此需要研究有效的方法對傳統無差拍電流預測中的電機參數擾動進行觀測與補償。

2.2 無差拍電流預測控制擾動問題

在數字控制系統中，由于采樣時間Ts非常小，通常認為轉速ωr在短時間內保持不變，因此系數a可被認為是常數。考慮到電機參數變化導致的擾動，采用前向歐拉法將式（3）離散化得到：

在實際數字系統中，實際電壓值為上一個PWM 周期計算得到的給定電壓值，即電壓存在一步延時，因此式（23）應改為：

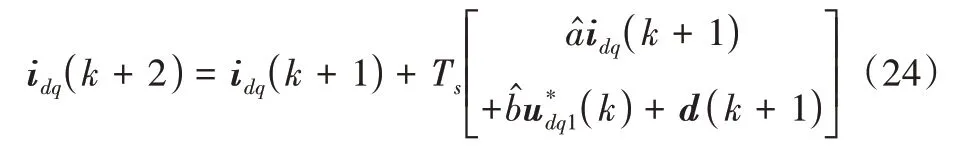
為實現無差拍控制，應使idq(k+2)跟蹤電流給定值，因此得到電壓給定值

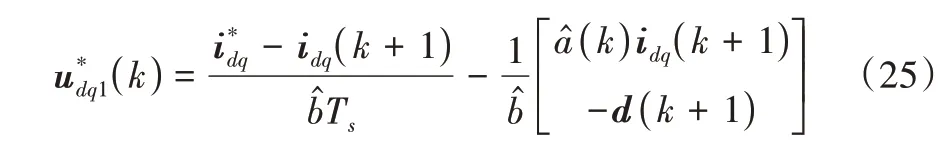
式（25）中，電流idq(k+1)和d(k+1)在k采樣時刻是未知的，因此需要對其進行預測。假設其預測值分別為，則可將式（25）修改為：

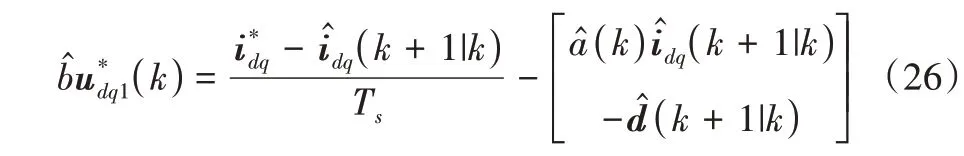
2.3 擾動與電流預測

考慮數字系統一步延遲時，第k+1 采樣時刻的電流可根據電流狀態方程預測得到：

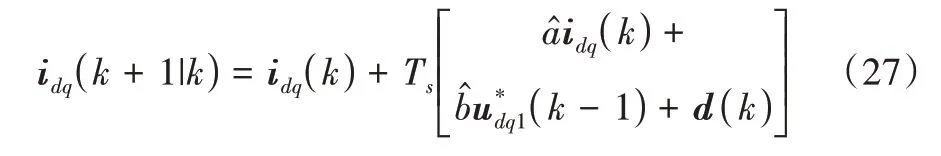
這一預測方法被廣泛應用于有限集模型預測控制中，但此方法是在假設系統不存在擾動的情況下實現的。當系統存在擾動，例如電機參數不匹配導致的擾動時，該方法將不再適用，需要對擾動進行觀測。為此，本文采用自抗擾控制系統中已有的ESO 對電流和擾動進行預測。

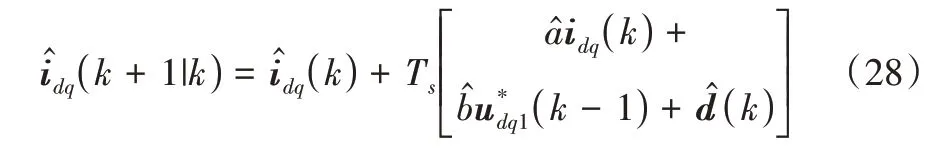
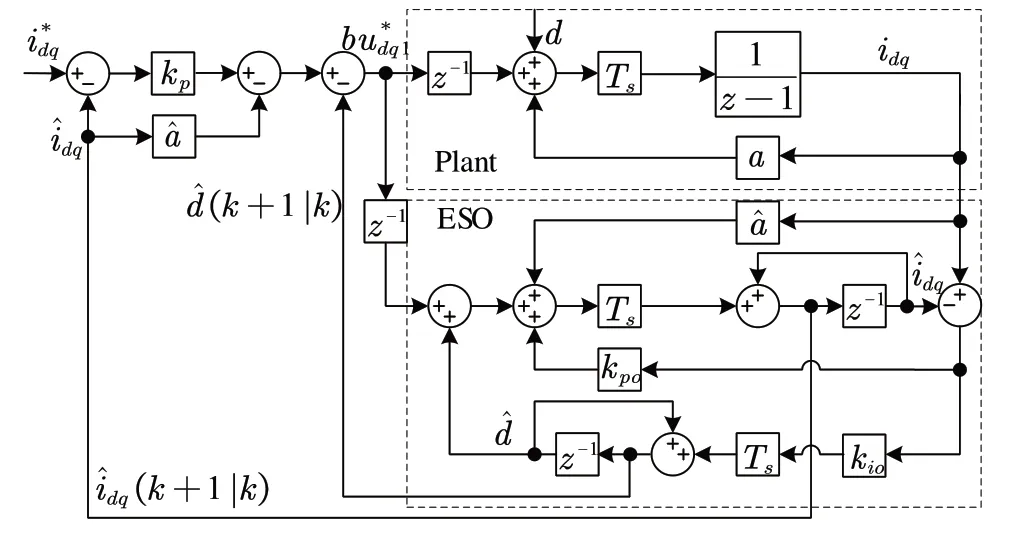
Fig.5 Structure block diagram of deadbeat active disturbance rejection current control system圖5 無差拍自抗擾電流控制系統結構框圖

綜上，無差拍自抗擾控制系統結構框圖如圖6所示。

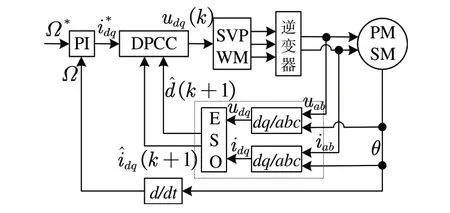
Fig.6 Structure block diagram of deadbeat ADRC system圖6 無差拍自抗擾控制系統結構框圖

3 實驗驗證與分析

為驗證所提控制方法的有效性，本文進行了實驗驗證。本實驗平臺永磁同步電機調速系統采用基于dSPACE 的實時仿真系統DS1103，利用快速原型法通過Simulink 自動完成代碼生成與下載。實驗中的逆變器開關頻率為10kHz，控制系統的硬件設備如圖7所示。

PMSM 控制系統的電機參數如表1所示。

實驗中，速度環采用PI 控制器，電流環分別采用傳統預測控制器和無差拍自抗擾預測控制器。根據實驗測試結果，選取ADRC 控制器參數為：ωn=1 000。速度環中的PI控制器參數設置為kps=0.01，kis=30。首先在電機參數準確時進行驗證，然后改變電機參數進行參數魯棒性驗證。

3.1 無差拍電流預測實驗

Fig.7 Experimental equipment圖7 實驗設備

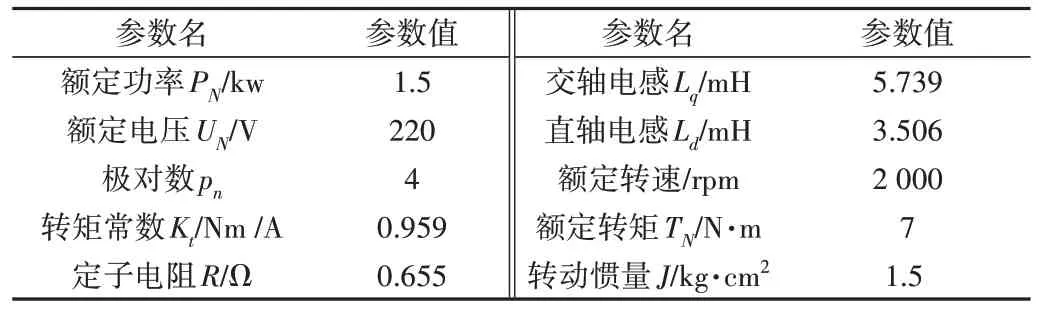
Table 1 Motor parameters表1 電機參數

在電機參數準確時，轉速給定由500rpm 階躍到700rpm，實驗波形如圖8 所示。iqest表示預測電流，iqfdb表示反饋電流。實驗波形上部分為傳統無差拍預測實驗波形，下部分為無差拍自抗擾預測實驗波形。由圖可以看出，使用ESO 實現的電流預測與傳統預測是一致的，在傳統預測基礎上增加的ESO 不會影響電流的快速響應性能。相對于反饋電流，預測電流可實現超前一步。

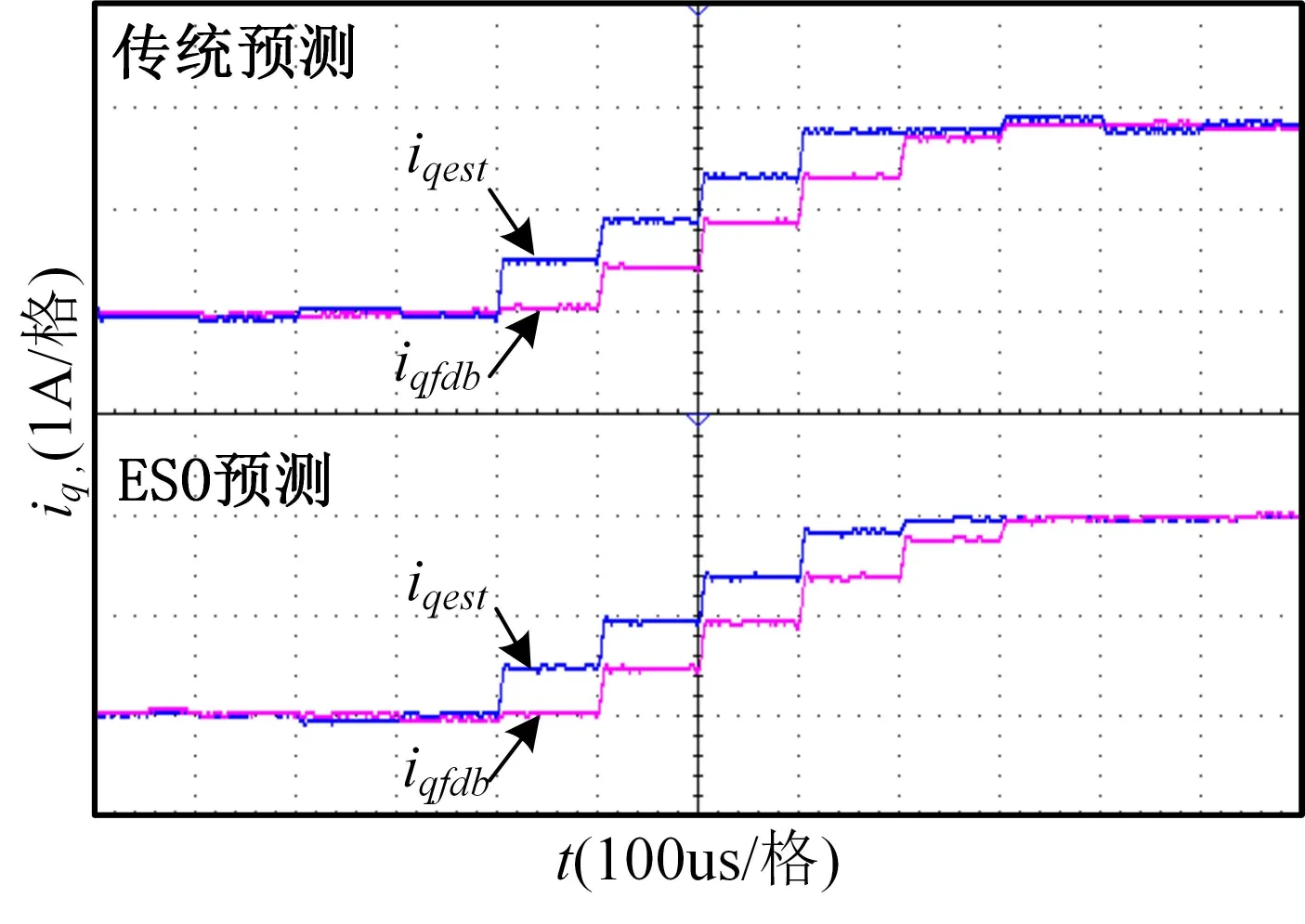
Fig.8 Experimental waveform of deadbeat prediction current control圖8 無差拍電流預測實驗波形

3.2 系統參數魯棒性實驗

驗證系統在電機電感失配下參數的魯棒性，分別改變電感至原來的2 倍和0.3 倍，實驗波形如圖9、圖10 所示。iqref表示給定電流表示估計電感，Ldq表示實際電感。給定轉速由600rpm 階躍至800rpm，由圖可以看出，在傳統無差拍預測控制下，電感失配2 倍時電流已經振蕩，這與前面的理論分析一致。在電感變小時也會在階躍響應時引起預測電流較小的振蕩，這是因為電感失配較大時施加到電機上的電壓存在抖動所致。而使用ESO 進行預測的電流可以實現穩定運行，這是由于ESO 對電感失配造成的擾動進行了實時觀測和補償，控制系統具有較強的魯棒性。

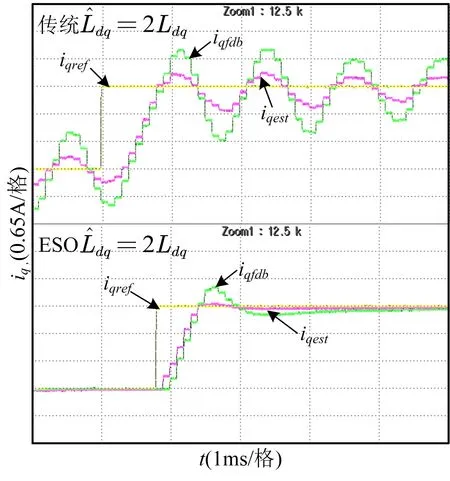
Fig.9 Experimental waveform in case of 2 time of inductance mismatch圖9 電感失配2倍下的實驗波形

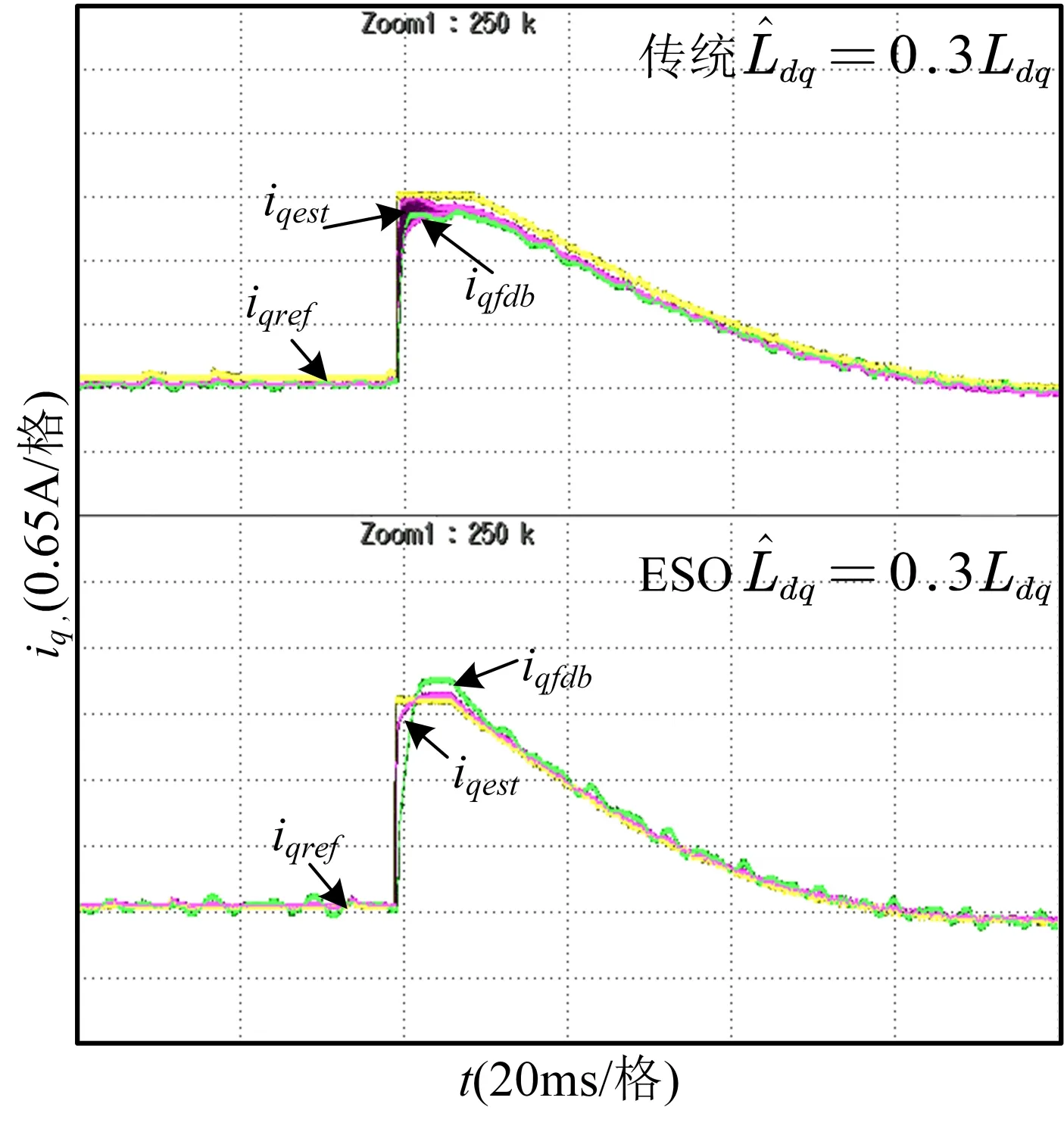
Fig.10 Experimental waveform in case of 0.3 times of inductance mismatch圖10 電感失配0.3倍下的實驗波形

其次驗證系統在磁鏈失配情況下的參數魯棒性，電機轉速恒定在700rpm，然后分別改變磁鏈至原來的1.5 倍和0.5 倍。表示估計磁鏈，ψf表示實際磁鏈。實驗波形如圖11 所示。由圖可以看出，傳統預測實驗在磁鏈失配時會產生電流跟蹤穩態誤差，這與前面的理論分析相符，而設計的ESO 可以利用對擾動的估計進行補償，實現無穩態誤差的電流跟蹤，提高了系統的控制性能。

最后驗證系統在電阻失配情況下的參數魯棒性，由于電阻對系統造成的影響很小，因此只進行了電阻改變為原來8倍的實驗。表示估計電阻，Rs表示實際電阻，給定轉速由600rpm 躍至800rpm。由圖12 可以看出，傳統預測在電阻變為原來的8 倍后，由于電阻失配造成電壓擾動導致施加到電機上的總電壓增加，因此在階躍時反饋電流要比給定電流大。而使用ESO 對擾動電壓進行觀測與補償后，可以實現擾動的快速收斂，因此設計的無差拍自抗擾系統對電阻也有較好的魯棒性。

從實驗結果可以看出，在電機參數準確時，兩種控制方法都可實現電流的快速響應。在電機參數變化時，通過在傳統無差拍電流預測控制中引入擴張狀態觀測器，可在實現電流預測的同時，大幅改善傳統無差拍控制依賴參數的問題，提高了系統參數的魯棒性，實驗結果與理論分析結果一致。

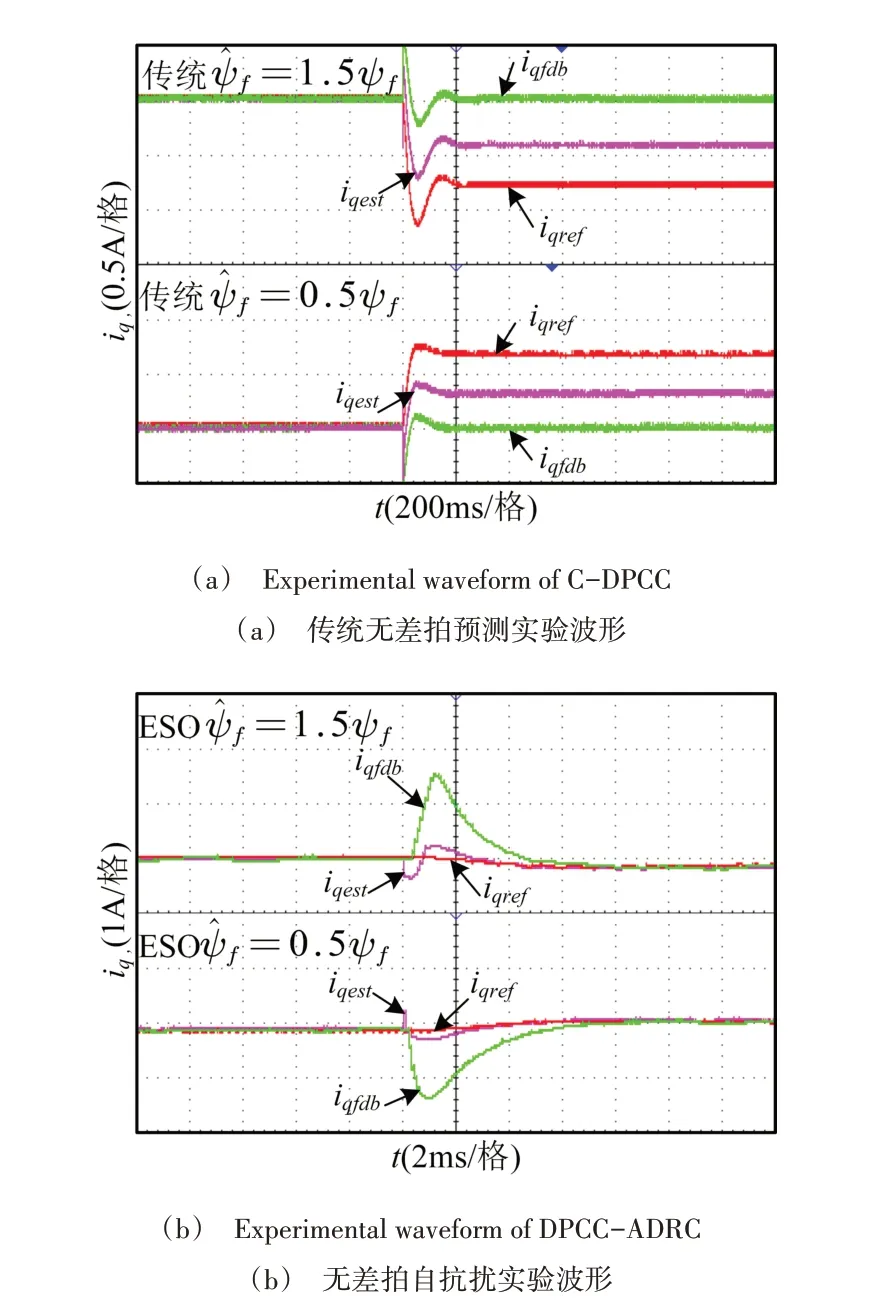
Fig.11 Experimental diagram in case of flux mismatch圖11 磁鏈失配下的實驗波形

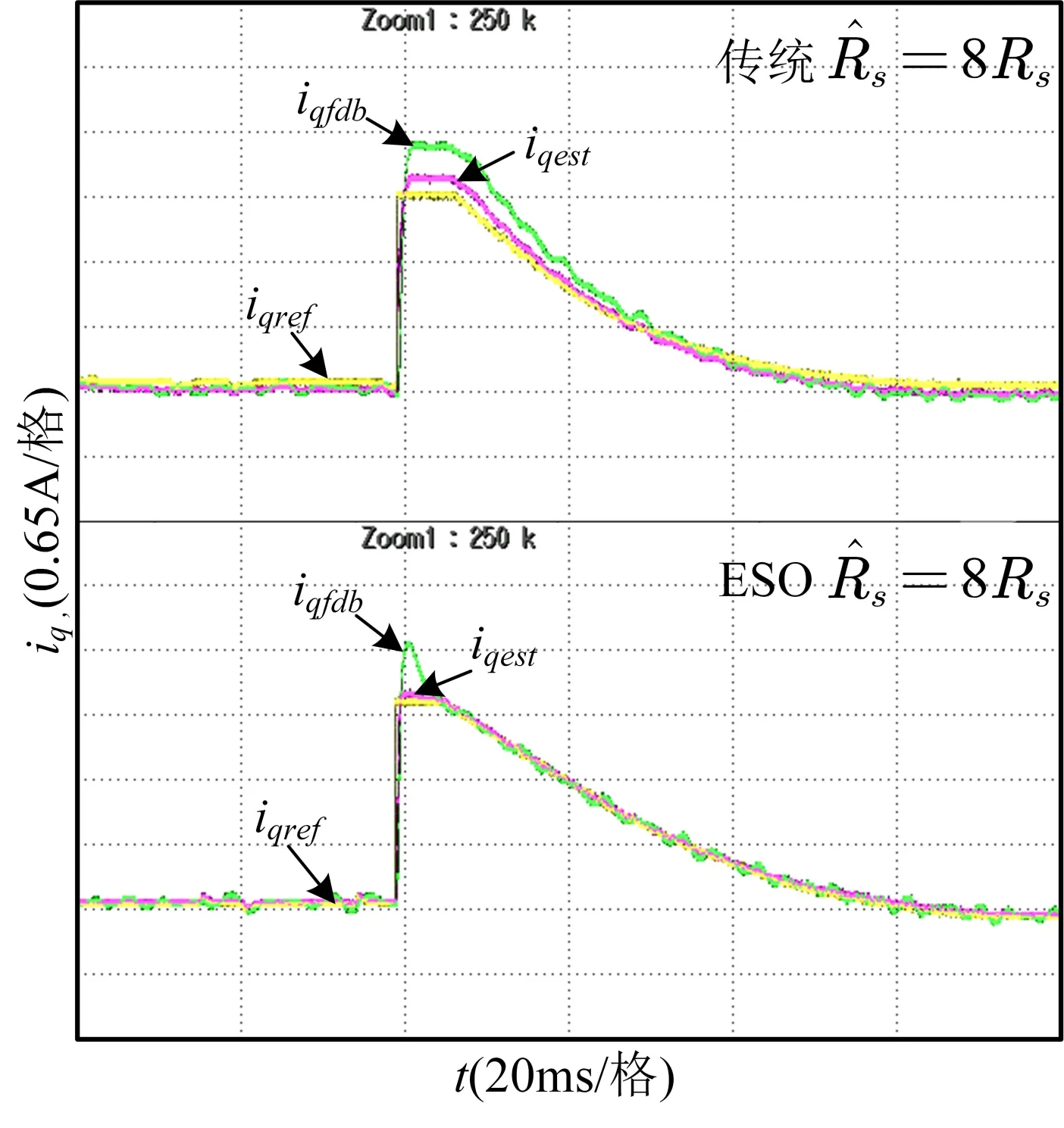
Fig.12 Experimental waveform in case of resistance mismatch圖12 電阻失配下的實驗波形

4 結語

針對傳統無差拍電流預測控制參數魯棒性較差的問題，本文提出一種基于自抗擾的無差拍預測電流控制算法。實驗結果表明，無差拍自抗擾控制可以極大地增強系統參數的魯棒性。然而，在電機的實際運行過程中，電機的電感、電阻和磁鏈有可能同時發生變化，并且變化范圍不一定在本文所設定的范圍內，因此后續需要在此基礎上，研究在多變量變化以及在參數變化范圍較大時依然具有較好魯棒性的無差拍自抗擾控制方法。