高速行車條件下鋼軌焊接接頭區輪軌動態相互作用
楊春凱 陳嶸 王攀杰 孫耀亮 安博洋 王平
1.西南交通大學高速鐵路線路工程教育部重點實驗室,成都 610031;2.西南交通大學土木工程學院,成都 610031;3.中鐵物總運維科技有限公司,北京 100071
TG/GW 115—2012《高速鐵路無砟軌道線路維修規則(試行)》對高速鐵路鋼軌焊接接頭不平順的管理尺寸要求為:200~250 km/h速度等級下1 m直尺測量范圍內焊接接頭平直度不得超過0.3 mm,250~350 km/h速度等級下不得超過0.2 mm。然而,在平直度相同的情況下,不同波長的焊接接頭幾何不平順會引起不同的輪軌動力響應[8]。因此有必要研究高速行車條件下焊接接頭區輪軌動態相互作用,以有效控制焊接接頭幾何不平順尺寸。文獻[9]發現短波不平順波長和幅值是影響安全限值的主要因素。文獻[10-11]利用車輛-軌道耦合系統動力學模型分析了焊接接頭幾何不平順的波長和波深對輪軌垂向力的影響,發現焊縫區輪軌垂向力隨波長增加而逐漸減小。文獻[12]基于車輛-整體道床軌道垂向耦合模型,發現當焊接接頭不平順波長小于某一臨界值時輪軌動力響應會急劇增大。
上述研究均是先假定鋼軌焊接接頭幾何不平順波形為余弦或其疊加形式,再通過不平順波長或波深提出鋼軌接頭幾何限值。實際上,鋼軌接頭的實測幾何形狀與理想波形存在較明顯的差異,上述研究成果的應用范圍受限。為考慮實測鋼軌焊接接頭幾何不平順,文獻[13]提出一種利用幾何梯度來評估焊接接頭質量的方法,假定輪軌垂向力與實際鋼軌接頭的幾何梯度呈線性關系,并基于數值計算和工程經驗確定了相關系數和標準。在此基礎上,文獻[14]提出了特征深度的方法,并借助于三維輪軌瞬態滾動接觸模型獲得了適用于300 km/h高速線路的相關系數,顯著地提高了預測精度。
目前,我國正在修建運行時速達400 km的高速鐵路。隨著列車運行速度進一步提高,列車對鋼軌焊接接頭的沖擊也會加劇。本文在既有研究的基礎上開展400 km/h速度下鋼軌焊接接頭處的輪軌相互作用的研究,并提出相應的評估方法。
1 基于幾何梯度的鋼軌接頭幾何不平順評價方法
文獻[15]中,假定鋼軌焊接接頭幾何梯度與其激發輪軌垂向力的最大波動幅值Fd,max存在線性關系,即
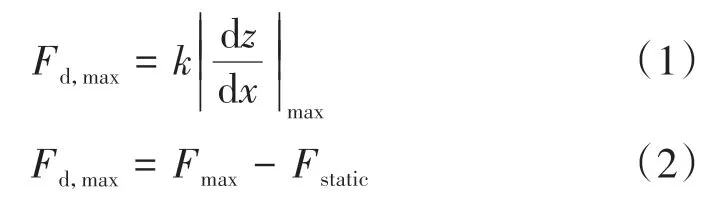
式中:Fmax和Fstatic分別為最大輪軌垂向力、靜輪載;k為與速度相關的系數;|dz/dx|max為鋼軌接頭幾何不平順沿縱向分布的最大梯度。
顯然,線性關系是一種簡化處理方式,文獻[14]對此進行了兩個改進。①提出了特征深度的概念,結合幾何梯度即可考慮與之相關的波長成分;②利用三維輪軌滾動瞬態滾動接觸有限元模型獲得了更為準確的輪軌接觸力與幾何梯度的定量關系。本文在此基礎上,進一步建立適用于400 km/h高速鐵路輪軌接觸力與幾何梯度的定量關系。
研究400 km/h高速行車條件下的輪軌滾動沖擊問題,需要考慮輪軌系統的柔性變形以及高頻振動。因此,采用三維輪軌瞬態滾動接觸有限元模型進行模擬[16]。其中,輪軌系統采用實體單元模擬;施加轉矩M以考慮牽引工況下的輪軌滾動接觸狀態;車輪踏面廓形采用LMA,輪徑取860 mm;鋼軌廓形采用CHN60,并設置1∶40的軌底坡;為提高計算效率,車體和轉向架簡化為質點并通過一系懸掛與輪對相連。有限元模型見圖1。圖中:Ks和Cs分別為一系懸掛的剛度系數和阻尼;Mc為簧上質量;x、z分別為水平縱向和垂向坐標;λ為不平順波長;v為車速。

圖1 有限元模型(單位:m)
考慮兩種鋼軌焊接接頭幾何不平順類型:①理想化的焊接接頭幾何不平順;②由某高速線路實測獲得的幾何不平順。前者用于建立輪軌接觸力與鋼軌接頭幾何不平順的定量關系,后者則用于驗證該定量關系的有效性。其中,理想化的鋼軌焊接接頭幾何不平順的表達式為
對數據分析后發現,數據差異基本都滿足要求,除去個別差距在5%,其余所有數據誤差均在誤差范圍之內,因此,本程序中的風荷載計算模塊是可靠的。
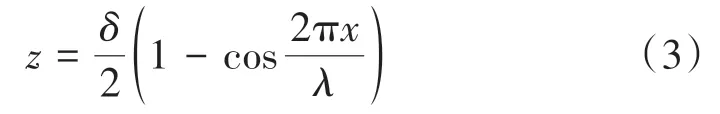
式中:δ為不平順波深。
對式(3)兩邊求一階導數,可得到理想鋼軌焊接接頭幾何梯度的表達式,即
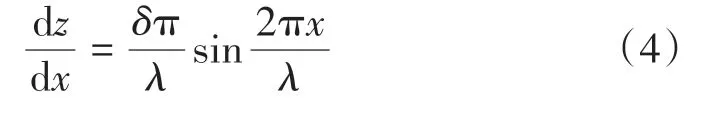
2 鋼軌焊接接頭區輪軌動力相互作用
2.1 鋼軌焊接接頭區的輪軌動態沖擊響應
以δ=0.15 mm,λ=0.05、0.10、0.30 m的鋼軌接頭幾何不平順為例進行分析。計算車輪以400 km/h通過這三種鋼軌接頭時所激發的輪軌動態力,并與焊接接頭幾何梯度沿軌道縱向的變化曲線進行對比,結果見圖2。其中輪軌動態力為輪軌垂向力減去靜輪載后的結果。
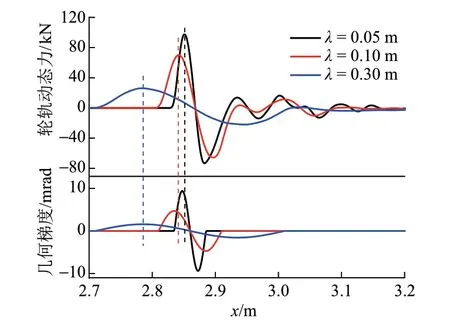
圖2 列車以400 km/h通過不同波長鋼軌焊接接頭區的輪軌動態力時程曲線
由圖2可知:接頭不平順激發的輪軌動態力變化與接頭幾何梯度的變化趨勢一致,最大輪軌動態力出現在幾何梯度最大值附近;接頭越平緩(對應較小的幾何梯度),激起的輪軌動態力越小。
λ=0.10 m時,δ=0.05、0.10、0.15、0.20 mm對應的最大幾何梯度分別為1.57、3.14、4.71、6.28 mrad。車輪以400 km/h通過時所激發的最大輪軌動態力與最大幾何梯度的關系見圖3。可知,最大輪軌動態力隨不平順最大幾何梯度增大而線性增大。顯然,輪軌動態力隨不平順波深增大而線性增大,這為利用線性插值預測輪軌動態力提供了依據。
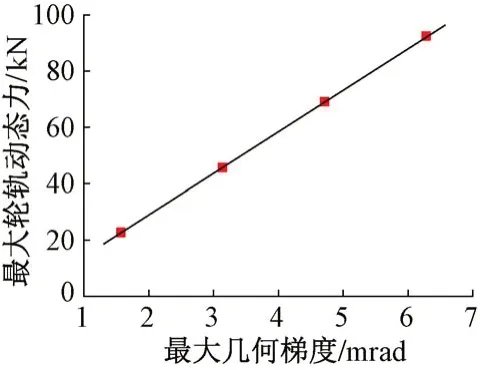
圖3 λ=0.10 m時最大輪軌動態力與最大幾何梯度的關系
2.2 輪軌動態力和幾何梯度的關系
鋼軌焊接接頭波長和波深的不同導致的幾何梯度變化對輪軌動態力的影響顯著。因此,建立最大輪軌動態力與最大幾何梯度的定量關系,結果見圖4。其中包含0.05、0.10、0.15、0.20 mm四種典型波深,幾何梯度的變化通過改變波長實現。
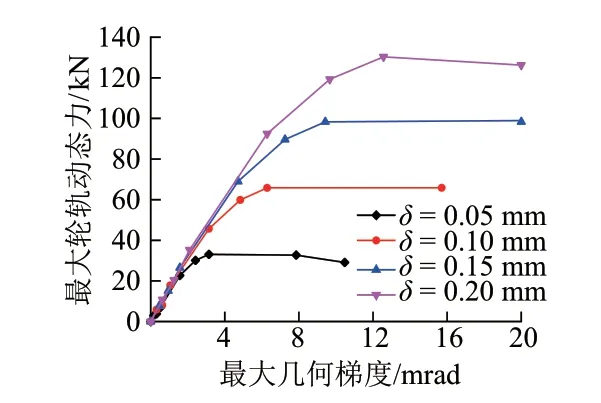
圖4 不同波深下最大輪軌動態力與最大幾何梯度的關系
由圖4可知:①以δ=0.10 mm為例,當焊接接頭最大幾何梯度小于3.14 mrad(對應λ=0.10 m)時,最大輪軌動態力隨最大幾何梯度增大而線性增大;隨著最大幾何梯度進一步增大,最大輪軌動態力由線性增加轉為非線性增加,達到極大值后不再發生明顯變化,說明最大輪軌動態力不會隨波長減小而無限增大,這是由于輪軌接觸區存在濾波作用,即波長小于或接近接觸斑特征尺寸時,不平順對輪軌的激勵作用將被削弱[17]。②隨著波深增加,最大輪軌動態力的極值也逐漸增大,波深增至0.20 mm時最大輪軌動態力極值增至130 kN。根據TB 10621—2014《高速鐵路設計規范》,無砟軌道結構豎向設計荷載動載系數取3.0,即最大輪軌垂向力可取靜輪載的3倍。本文選取的輪對軸重為15 t,單輪靜載值為73.5 kN,因此波深為0.2 mm時,最大動態系數約為2.77,小于線路設計時選用的3倍動態系數。
3 實測鋼軌焊接接頭不平順評估
利用線性插值預測輪軌動態力,對實際鋼軌焊接接頭幾何不平順進行動力評估,并以瞬態接觸模型的計算結果作為參考。
選取我國一高速線路20個實測典型焊接接頭幾何不平順(圖5)作為鋼軌不平順激擾輸入量進行仿真計算。計算時,列車運行速度取400 km/h。
1#實測焊接接頭的幾何分布及通過有限元仿真計算得到的輪軌垂向力變化曲線見圖6。可知:該接頭最大幾何梯度為1.90 mrad;仿真計算得到的最大輪軌垂向力為94.56 kN。根據輪軌動態力與幾何梯度的關系曲線(參見圖4),可預測1#實測焊接接頭引起的輪軌動態力幅值為25.57 kN,疊加靜輪載后最大輪軌垂向力為99.07 kN,這與仿真計算結果很接近。
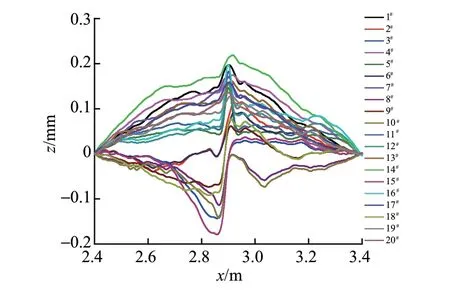
圖5 20例實測焊接接頭幾何分布

圖6 1#實測焊接接頭的幾何分布及輪軌垂向力仿真計算結果
2#實測焊接接頭的幾何分布及通過有限元仿真計算得到的輪軌垂向力變化曲線見圖7。

圖7 2#實測焊接接頭的幾何分布及輪軌垂向力仿真計算結果
由圖7可知:該接頭最大幾何梯度為2.76 mrad;仿真計算得到的最大輪軌垂向力為113.94 kN。2#實測焊接接頭的最大幾何梯度達到2.76 mrad,超過了最大輪軌動態力與最大幾何梯度的關系曲線(參見圖4)的線性區域。這種情況需考慮特征深度的影響,根據文獻[13]提出的特征深度辨識方法,該鋼軌焊接接頭的特征波深為0.12 mm。由圖4及線性插值可以預測其最大輪軌垂向力為114.95 kN,與仿真計算結果的偏差僅0.89%。
20個實測焊接接頭的最大輪軌垂向力預測與仿真結果對比見表1。可知,除15#接頭外,其余接頭的預測與仿真結果偏差均在10%以內。這表明該方法能夠比較準確地預測實測鋼軌接頭幾何不平順引起的輪軌沖擊力。
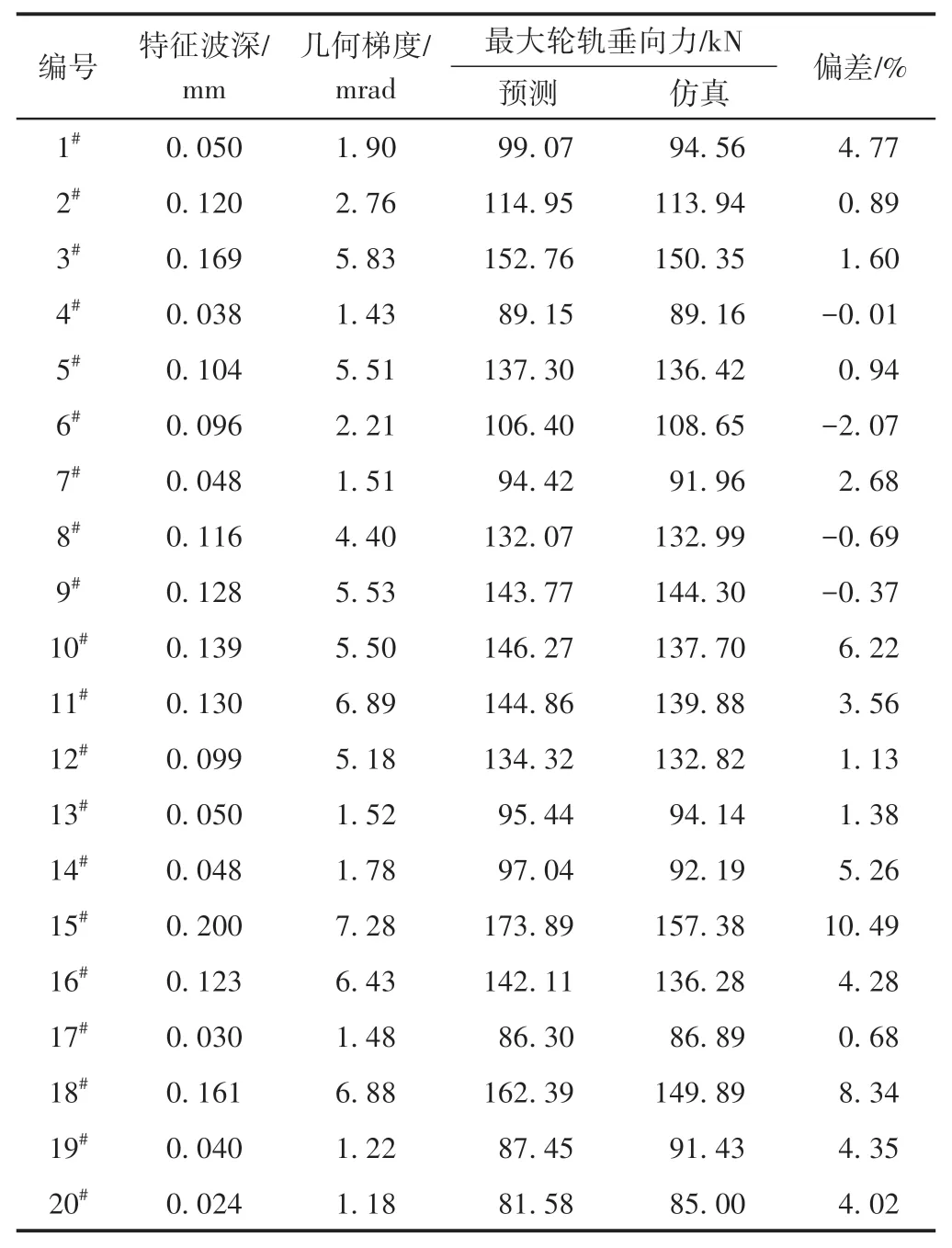
表1 焊接接頭最大輪軌垂向力預測與仿真結果對比
從15#實測焊接接頭的幾何分布(圖8)可知,其焊縫波深達到0.20 mm。車輪通過時未接觸到焊縫最深處,因此利用圖4進行預測時采用的波深偏大,導致預測結果偏大。
值得指出的是,有限元模型計算一個算例的時間大約為40 h,而本文預測方法不足1 s。本文方法可以有效地兼顧計算精度和效率,可用于現場快速評估焊接接頭幾何不平順處的最大輪軌動態力。

圖8 15#實測焊接接頭的幾何分布
4 結論
1)當焊縫幾何梯度較小時,最大輪軌動態力隨幾何梯度呈線性增長;隨梯度進一步增大,最大輪軌動態力由線性增加轉為非線性增加,達到極大值后,由于接觸濾波效應,最大輪軌動態力隨幾何梯度的增加不再發生明顯變化。
2)焊接接頭波深取0.2 mm,即平直度為0.2 mm時,列車以400 km/h通過焊縫,荷載最大動態系數約為2.77,小于線路設計時常選用的3倍動態系數,列車仍可安全運行。
3)利用本文所建立的輪軌動態力與鋼軌焊接接頭幾何梯度的關系,能快速有效地預測實測鋼軌焊接接頭幾何不平順處的輪軌動態力。

