磁共振成像磁體無源勻場改進策略及實驗研究

曲洪一 劉 鑫 王 暉 劉建華 王秋良,3

磁共振成像磁體無源勻場改進策略及實驗研究

曲洪一1,2劉 鑫2,3王 暉1劉建華1,2王秋良1,2,3

（1. 中國科學院電工研究所 北京 100190 2. 中國科學院贛江創新研究院 贛州 341000 3. 中國科學技術大學稀土學院 合肥 230026）

無源勻場用于修正磁共振成像磁體不均勻的磁場，是一個非常耗時的過程，包括磁場測繪、優化分析、方案制定、工程實施等步驟。由于存在不可避免的計算誤差，無源勻場需要多次重復以上步驟（迭代）才能獲得滿足要求的高均勻度靜磁場，目前相關研究主要集中于優化模型的構造或求解算法的改進，研究手段通常是數值模擬法，忽略了勻場實踐中遇到的問題，更沒有基于勻場過程工藝的優化。為了提高勻場的性能和效率，該文提出了一些磁共振成像（MRI）磁體無源勻場技術的改進策略：測量多個樣片的實際磁場以校正磁化場計算；以目標磁場為變量構建線性優化模型；采用“奇偶”勻場法減少勻場系統的拆裝次數。最后，在一臺1.5T MRI超導磁體上實施了改進的無源勻場技術驗證實驗，結果顯示，僅通過兩次迭代即可獲得滿足成像要求的磁場均勻度，并且在第三次迭代后達到設計值。與改進前的實驗結果相比，新的勻場策略具有顯著的成效。

磁共振成像磁體 無源勻場 校正模型 “奇偶”勻場法

0 引言

磁共振成像（Magnetic Resonance Imaging, MRI）設備已成為醫學診斷中最強有力的工具之一，并成為癌癥早期診斷、高風險手術評估、代謝成像和神經科學的重要研究工具[1-2]。磁場均勻度是評估MRI磁體質量重要的指標之一，盡管電磁設計可以使磁體達到很高的磁場均勻度，但在實際制造過程中，各種因素使得磁體線圈偏離理想位置，加之不可避免的計算誤差，導致了磁場偏差（不均勻性）的產生。磁場偏差會使磁共振圖像產生錯位或者模糊等問題，圖1為磁場不均勻導致的偽影和脂肪抑制問題[3]。因此，MRI磁體出廠前需要進行一系列檢測和校準，使其達到成像均勻度的標準[4]。無源勻場是一種提高磁場均勻度的補救措施[5-10]，其原理是：在磁體的室溫孔區域安裝一定數量的鐵磁介質，形成特定的分布組合。分布組合中的鐵磁介質被磁化后會產生特定的磁場場型來“墊補”不均勻的磁場。鐵磁介質產生的磁化場的精確計算是無源勻場關鍵技術難題之一，特別是需要考慮到不飽和磁化和整數化問題的時候[11-14]。圓柱式結構是MRI磁體應用最廣泛的結構類型，其無源勻場系統的設計是在磁體室溫孔壁環繞固定多組勻場條。為了勻場條的穩定和對稱，常將勻場系統與梯度系統耦合設計。勻場條可沿磁體室溫孔軸向拔插，內含若干勻場槽用以放置鐵磁介質。在大多數圓柱形磁體中，與軸向磁感應強度相比，徑向磁感應強度較小，可以忽略不計，因此，鐵磁介質的磁化只需考慮軸向磁場的影響。在高場（一般指1.5～3T）MRI磁體中，鐵磁介質所處位置的磁感應強度較高，可認為被軸向磁場飽和磁化，簡化了計算模型，從而在一定程度上降低了無源勻場的難度。然而，磁體的徑向磁場在室溫孔端部位置數值較大，會對鐵磁介質的軸向磁化場強度造成一定的減弱，不可忽略，現有勻場技術文獻未涉及對端部徑向磁場“負作用”進行修正的措施。由于存在計算誤差，無源勻場的實施過程往往是一個耗時的迭代過程，每次迭代均需要磁場測量、優化分析、方案制定、工程實施等步驟。目前，相關文獻主要針對無源勻場優化算法的提出和改進，對工程、工藝實踐方面改進的報道較少。而實際上，真正影響無源勻場效率和耗時的往往是工程實踐。

圖1 磁場不均勻導致的圖像問題

為了提高MRI磁體無源勻場的精度和效率，減少勻場迭代次數，本文提出了一些無源勻場的改進策略，主要包括算法上構造鐵磁介質敏感矩陣校正模型和自動搜索最優目標磁場的線性規劃模型，工程上采取“奇偶”勻場法。最后，在一臺1.5T MRI超導磁體上實施了改進后的勻場驗證實驗，和未改進前相比，不僅磁場均勻度獲得提升，而且迭代次數減少了2次以上。

1 無源勻場優化設計

1.1 鐵磁介質磁化場計算

鐵磁介質被磁化產生的磁場為

其中

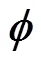
位于空間任意點處的磁矩d在空間任意點處產生的軸向（-）磁場為

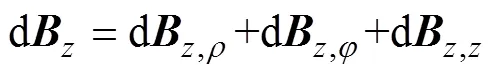
由于方向和方向磁場的貢獻度較小，為了簡化計算，忽略不計，然后利用計算值和實測值的最小化算法進行修正，因此，式（2）右項僅保留第一項。文獻[15-16]給出了鐵磁介質磁化場的詳細計算公式。

鐵磁介質計算中涉及到非線性、飽和、磁滯等多種問題，與所選的材質密切相關[17]，在無源勻場技術中，一般選用磁導率高、矯頑力低、磁滯小的鐵磁材料，如硅鋼等。

1.2 鐵磁介質磁化場校正

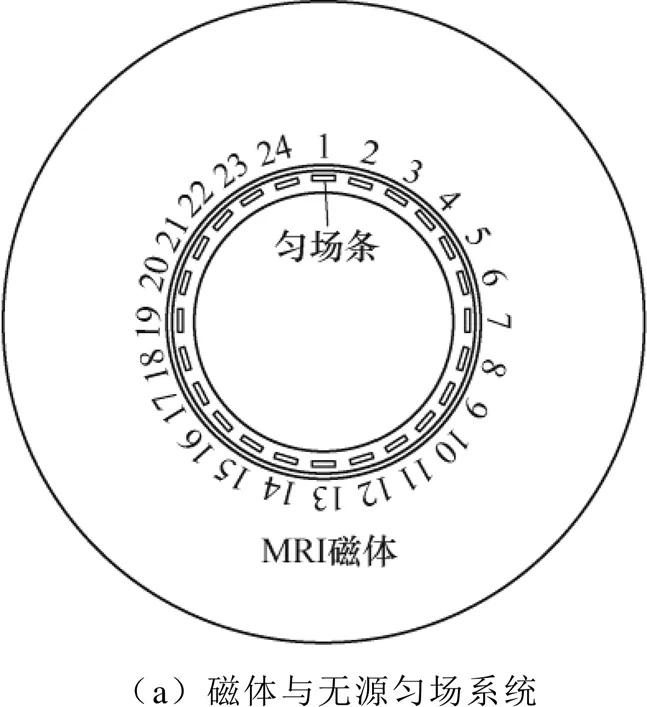
本次實驗研究的對象是圓柱形MRI超導磁體，無源勻場系統如圖2所示，磁體室溫孔預置24組環向均勻排列的勻場條，沿勻場條長軸方向設置22個勻場槽。為方便闡述，勻場條和勻場槽均賦予標號。

由于位于磁體端部勻場槽的鐵磁機制計算誤差較大，可適量增加參與校正的勻場槽，磁體中心的計算誤差較小，考慮計算量，勻場槽可以減少。參數和的值可以通過Matlab求解，獲取和的值后，再對測試磁體進行校正計算。事實上，和的值與硅鋼片的磁化率和徑向磁場的貢獻度有關，用于修正假定飽和磁化和忽略徑向磁場造成的誤差。圖3為本次實驗中，勻場槽1、3、6、11中硅鋼片產生的未校正計算、校正計算和實際測量的磁感應強度比較結果。從圖3中可以看出，相對于未修正的計算結果，校正后的計算值更接近于測量值。

圖3 勻場槽中硅鋼片產生的未校正、校正后和實測的磁場值對比

1.3 動態目標磁場的優化模型

將式（1）～式（3）聯立，可以計算出校正后的敏感矩陣，其維數為×，其中為磁場采樣點數，為勻場槽總數。敏感矩陣為每個勻場槽中單位厚度的鐵磁介質在每個采樣點處產生的軸向磁場。若放置厚度為的鐵磁介質片后，采樣點的磁場將變為m，那么均勻度表述為

以鐵磁介質的總消耗量為目標函數，磁場均勻度和勻場槽可放置鐵磁介質的最大厚度為約束條件，無源勻場的線性規劃模型可表示為

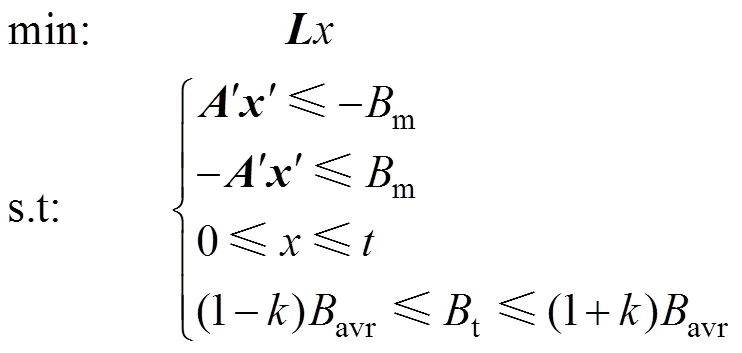
其中

2 實驗研究

對提出的無源勻場改進策略進行了實驗研究，實驗平臺為一臺室溫孔徑850mm，磁感應強度1.5T的MRI超導磁體，如圖4所示，實驗平臺已安裝梯度系統與磁場測量系統，并在梯度系統中預留勻場條拔插孔。磁場測量區域為磁體中心450mm直徑的球形區域（Diameter Spherical Volume, DSV）。

圖4 嵌入無源勻場系統的1.5T超導磁體

2.1 實驗設計

無源勻場是一個繁瑣、耗時的過程，主要步驟包括磁場測量、優化分析、勻場鐵磁介質的放置和勻場條的安裝固定等，并且以上步驟隨著多次迭代而反復進行，工程量較大。此外，由于MRI磁體的磁場對鐵磁介質具有磁場力作用，致使勻場條受力不均勻且不易控制。因此，勻場條的安裝（插拔）具有一定的危險性，可能致使人員受傷、設備損害等情況的發生，特別是大量鐵磁介質集中于一根勻場條的情況，至少需要兩名有經驗的操作人員才能完成拔插步驟。在無源勻場實驗過程中，為了減少勻場條拔插次數，降低危險性，實驗采用了“奇偶”勻場法：第1次迭代，使用奇數標號的12根勻場條進行粗勻，將磁場均勻性提高到較好的水平。后序迭代均使用剩余偶數標號的勻場條進行細勻，勻場條的標記方式如圖2a所示。利用該方法，在每次勻場迭代中，最多只需拔插12根的勻場條，工作量和危險性均大大降低。

本次采用的MRI磁體初始磁場分布如圖5所示，磁場的均勻度采用區域的百萬分之一（part per million, ppm）來評估[22]。一般有兩種評估標準，峰峰值均勻度與體積方均根均勻度。峰峰值均勻度用于衡量磁場數據的最大偏差情況，體積方均根均勻度用于衡量磁場數據的離散情況，體積方均根均勻度的計算方法見文獻[23]。經計算，初始磁場在450mm DSV的峰峰值p-p均勻度和體積方均根（Volume Root Mean Square, VRMS）均勻度分別為378.09ppm和71.19ppm，磁場最大值和最小值位于球體兩極區域。

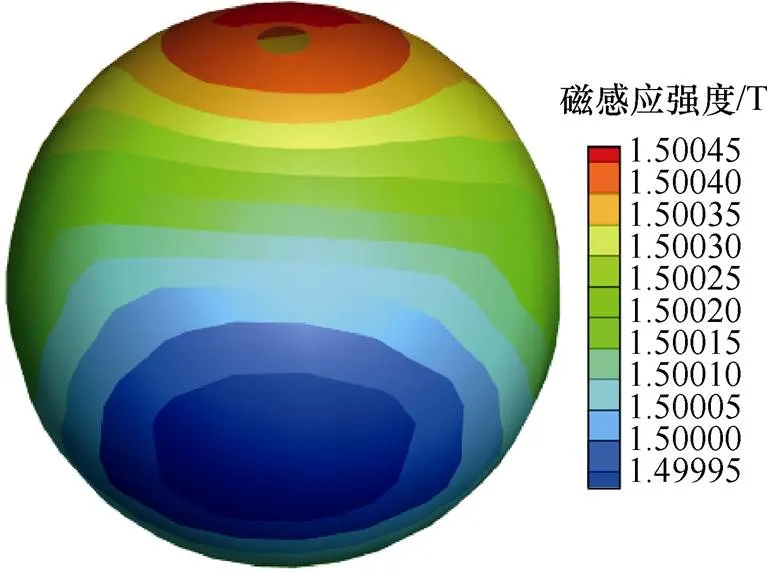
圖5 450mm DSV表面的初始磁場分布

2.2 改進前優化模型的實驗結果

表1 無源勻場的系統參數

表2 改進前模型的勻場實驗過程

Tab.2 The process of shimming experiment with unimproved model

2.3 改進后模型的實驗結果

在相同的實驗平臺下，采用改進后的優化模型進行無源勻場實驗，控制硅鋼片用量和改進前模型勻場實驗用量基本一致，優化參數設置一致。結果顯示，僅需要3次迭代即可完成勻場實驗，表3描述了改進后優化模型的勻場過程，其中，第2次迭代時，磁場滿足了VRMS＜2ppm的要求，第3次迭代時，磁場均勻度實測值和理論值一致。圖7為本次實驗峰峰值均勻度和體積方均根均勻度的收斂曲線，3次迭代過程中，硅鋼片和中心磁場空間分布如圖8～圖10所示，硅鋼片在每個勻場槽內的厚度見表4。

表3 改進后模型的勻場實驗過程

Tab.3 The process of shimming experiment with improved model

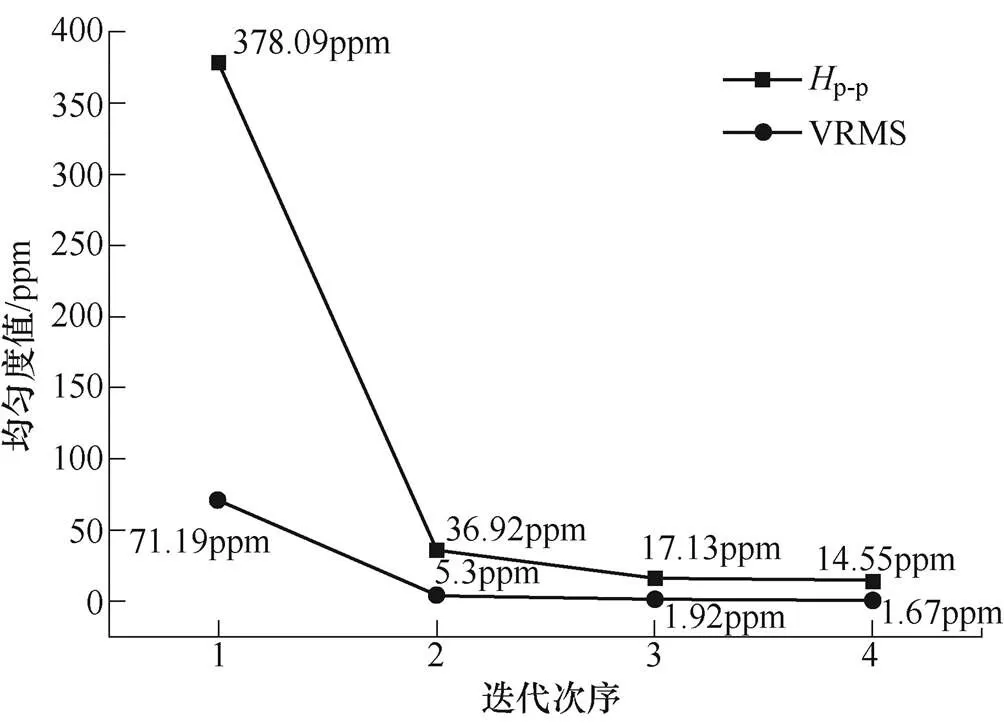
圖7 峰峰值Hp-p均勻度和體積方均根VRMS均勻度的收斂曲線

3 討論

對于無源勻場，勻場片磁化場計算的準確度直接決定了勻場迭代的次數。使用改進前的優化模型，需要5次迭代才能完成勻場實驗，但仍未達到理論值。使用改進后的優化模型，同一臺磁體只需要3次迭代即可完成勻場實驗，其中，第2次迭代就達到了磁場成像均勻度的要求。本文提出的校正方法選擇幾個代表性位置的勻場槽作為測量對象，對放置其中的勻場片進行了實際磁場的測量，通過測量數據和計算數據的最小二乘擬合，獲得了校正參數和，在同一磁體下，該參數可以用于后續的所有勻場實驗。經過校正后的優化模型計算更精確，均勻度收斂性更好，因此，相比于過量迭代所付出的時間和人力成本，從準確度、效率、工作量、安全性等方面評估，本文所提出的校正策略都是一個更佳選擇。另一方面，采用的優化模型能夠自動搜尋最佳的目標磁場，使磁場均勻度和勻場片分布比預先設定固定目標磁場的優化模型更合理。此外，從表3和表4顯示的勻場結果觀察，可以發現，“奇偶”勻場法具有優越的便捷性和安全性，第1次迭代采用奇數標號的勻場條（12根）極大地提高了磁場均勻度，其中，峰峰值均勻度提升了90.2%，體積方均根均勻度提升了92.6%。第1次迭代使用了2.924kg的硅鋼片，占據了硅鋼片總消耗量的80%左右；在第2次迭代中，動用了偶數標號的12根勻場條，消耗0.672kg硅鋼片；在第3次迭代時，動用了11根勻場條，僅消耗0.071kg（約占總消耗量的2%）的硅鋼片即達到了磁場理論值。綜合兩次實驗，“奇偶”勻場法和采用24根勻場條的傳統方法相比，拔插次數上，“奇偶”勻場法僅需拔插勻場條35次，而傳統方法則需拔插100次以上，拔插次數大大減少，降低了工作量；安全性上，“奇偶”勻場法僅在第1次迭代時需拔插大質量的勻場條，而傳統方法5次迭代均需拔插大質量的勻場條，顯然“奇偶”勻場法便捷性和安全性要遠高于傳統方法。但值得注意的是，在MRI磁體的初始磁場均勻性非常差或磁感應強度較高的情況下，因“奇偶”勻場法每次迭代僅適用一半數量的勻場條，其勻場能力有可能不足以達成勻場目標，此時就必須采用傳統的方法。因此，在勻場方案制定和實施前，可采用預測的方式來評估“奇偶”勻場法是否能勝任勻場任務。預測計算對優化模型的準確性提出了較高的要求，再次凸顯了校正計算的重要性和必要性。

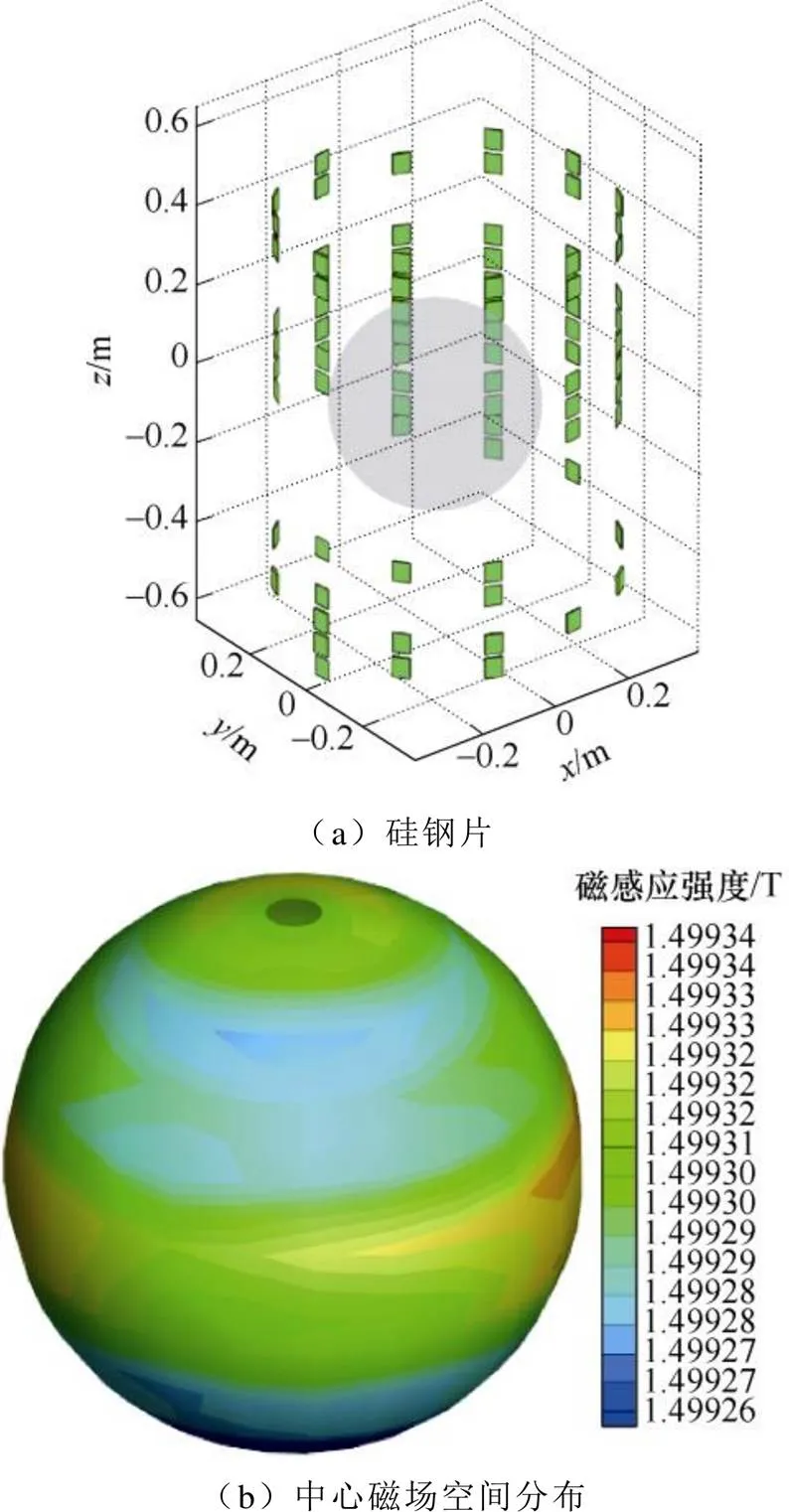
圖8 第1次迭代（粗勻）

圖10 第3次迭代（細勻）

表4 硅鋼片在每個勻場槽中的厚度

Tab.4 The thickness of the silicon steel pieces in each shim pocket （單位: mm）

第2次迭代

（續）

第3次迭代

4 結論

在MRI磁體的制造過程中，由于存在裝配誤差、周圍鐵磁材料的影響等因素，造成了磁場分布不均勻，從而影響磁體的成像效果。因此，通常采用無源勻場技術來提高磁場的均勻性。無源勻場是一個具有挑戰性的實踐工程，簡單的數值模擬研究遠遠不夠，有必要從方案的實際有效性出發。對此，本文提出了改進的無源勻場策略：利用實測值與計算值的最小二乘擬合，提高了勻場片的計算精度，且該方法修正了容易忽略的磁體端部徑向磁場的影響；所采用的優化模型中，將目標磁場設為未知參數，增加優化維度，可進一步提高尋解能力；選用一臺1.5T MRI超導磁體進行了實驗研究，在實驗過程中利用“奇偶”勻場法，有效減少了勻場系統的拆裝次數，降低過程中機械損傷風險。綜上所述，本文所提出的校正計算、優化模型以及“奇偶”勻場法適用于螺管式MRI超導磁體系統，在磁化場精確計算、勻場工作量及操作安全性等方面展現了較大的優勢，對相關研究人員具有一定的參考價值，在今后的研究中，將繼續基于勻場工程實踐中遇到的問題進行分析，力求能進一步提高計算的準確度，優化勻場工藝流程。

[1] 馮煥, 姜暉, 王雪梅. 功能磁共振成像在腫瘤學領域的應用[J]. 電工技術學報, 2021, 36(4): 705-716.

Feng Huan, Jiang Hui, Wang Xuemei. Application of functional magnetic resonance imaging in the field of oncology[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 705-716.

[2] 李曉南, 任雯廷, 劉國強, 等. 高分辨率磁共振電特性成像及腦腫瘤診斷初步研究[J]. 電工技術學報, 2021, 36(18): 3860-3866.

Li Xiaonan, Ren Wenting, Liu Guoqiang, et al. Preliminary conductivity reconstruction by high- resolution magnetic resonance electrical properties tomography for brain tumor diagnosis[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(18): 3860-3866.

[3] 張西亞. 磁場均勻度對MR圖像質量的影響[J]. 生物醫學工程與臨床, 2008, 12(3): 245-248.

Zhang Xiya. The effect of magnetic field homogenous level on the quality of MRI[J]. Biomedical Engin- eering and Clinical Medicine, 2008, 12(3): 245-248.

[4] 王秋良. 磁共振成像系統的電磁理論與構造方法[M]. 北京: 科學出版社, 2018.

[5] Belov A, Bushuev V, Emelianov M, et al. Passive shimming of the superconducting magnet for MRI[J]. IEEE Transactions on Applied Superconductivity, 1995, 5(2): 679-681.

[6] Frollo I, Andris P, Strolka I. Measuring method and magnetic field homogeneity optimization for magnets used in NUM-imaging[J]. Measurement Science Review, 2001,1(1): 9-12.

[7] Tang Wenju, Wang Hui, Li Yi, et al. An accurate passive shimming method[C]//8th International Con- ference on Information Technology in Medicine and Education (ITME), Fuzhou, China, 2016: 66-69.

[8] Abe M, Sakakibara K, Fujikawa T, et al. Static magnetic field shimming calculation using TSVD regularization with constraints of iron piece place- ments[J]. IEEE Transactions on Applied Super- conductivity, 2017, 27(7): 1-12.

[9] Kong Xia, Zhu Minhua, Xia Ling, et al. Passive shimming of a superconducting magnet using the L1-norm regularized least square algorithm[J]. Journal of Magnetic Resonance, 2016, 263: 122-125.

[10] Qu Hongyi, Niu Chaoqun, Wang Yaohui, et al. The optimal target magnetic field method for passive shimming in MRI[J]. Journal of Superconductivity and Novel Magnetism, 2020, 33(3): 867-875.

[11] Zhu Xuchen, Wang Houshen, Wang Hui, et al. A novel design method of passive shimming for 0.7T biplanar superconducting MRI magnet[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(7): 1-5.

[12] 武海澄, 劉正敏, 周荷琴. 磁共振成像永磁體的無源勻場方法[J]. 電工技術學報, 2007, 22(11): 7-11.

Wu Haicheng, Liu Zhengmin, Zhou Heqin. Research on passive shimming method for MRI permanent magnet[J]. Transactions of China Electrotechnical Society, 2007, 22(11): 7-11.

[13] You Xiaofei, Wang Zheng, Zhang Xiaobing, et al. Passive shimming based on mixed integer pro- gramming for MRI magnet[J]. Science China Tech- nological Sciences, 2013, 56(5): 1208-1212.

[14] Zhang Yanli, Xie Dexin, Bai Baodong, et al. A novel optimal design method of passive shimming for permanent MRI magnet[J]. IEEE Transactions on Magnetics, 2008, 44(6): 1058-1061.

[15] So N. Formulation of the spherical harmonic coefficients of the entire magnetic field components generated by magnetic moment and current for shimming[J]. Journal of Applied Physics, 2014, 115(16): 163908.

[16] Liu Feng, Zhu Jianfeng, Xia Ling, et al. A hybrid field-harmonics approach for passive shimming design in MRI[J]. IEEE Transactions on Applied Superconductivity, 2011, 21(2): 60-67.

[17] Furlani E P. Electromechanical devices[M]// Amsterdam: Elsevier, 2001: 335-467.

[18] 潘子君, 潘成, 唐炬, 等. 基于圖像復原技術與約束最小二乘方濾波器的絕緣子表面電荷反演算法[J]. 電工技術學報, 2021, 36(17): 3627-3638.

Pan Zijun, Pan Cheng, Tang Ju, et al. Inversion algorithm for surface charge on insulator based on image restoration technology and constrained least square filter[J]. Transactions of China Electro- technical Society, 2021, 36(17): 3627-3638.

[19] Qu Hongyi, Wang Yaohui, Niu Chaoqun, et al. A novel strategy and test of passive shimming for multi-volumes in cylindrical MRI scanner[J]. IEEE Transactions on Magnetics, 2020, 56(2): 1-7.

[20] 袁佳歆, 曲鍇, 鄭先鋒, 等. 高速鐵路混合儲能系統容量優化研究[J]. 電工技術學報, 2021, 36(19): 4161-4169, 4182.

Yuan Jiaxin, Qu Kai, Zheng Xianfeng, et al. Optimizing research on hybrid energy storage system of high speed railway[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4161-4169, 4182.

[21] 李少巖, 任乙沛, 顧雪平, 等. 基于短路電流約束顯式線性建模的輸電網結構優化[J]. 電工技術學報, 2020, 35(15): 3292-3302.

Li Shaoyan, Ren Yipei, Gu Xueping, et al. Optimization of transmission network structure based on explicit linear modeling of short circuit current constraints[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3292-3302.

[22] 曲洪一. 高場磁共振成像主磁體電磁優化方法研究[D]. 北京: 中國科學院大學, 2020.

[23] Ping Xuewei, Wang Mingyu, Yin Xinghui, et al. Evaluation of VRMS homogeneity of the magnetic field in MRI with numerical methods[C]//International Applied Computational Electromagnetics Society Symposium-China (ACES), Nanjing, China, 2019: 1-2.

Improved Strategy and Experimental Research on Passive Shimming in Magnetic Resonance Imaging Magnet

1,22,311,21,2,3

（1. Institute of Electrical Engineering Chinese Academy of Science Beijing 100190 China 2. Ganjiang Innovation Academy Chinese Academy of Sciences Ganzhou 341000 China 3. College of Rare Earths University of Science and Technology of China Hefei 230026 China）

Passive shimming is used to correct the inhomogeneous magnetic field of the MRI magnets. Due to the inevitable calculation errors, passive shimming must be repeated many times (iteration) to obtain a required high homogeneous static magnetic field. At present, the relevant research mainly focuses on constructing the optimization model or improving the solution algorithm. The research method is usually the numerical simulation method, ignoring the problems encountered in the shimming practice, and there is no optimization based on the shimming process. To improve the performance and efficiency of shimming, this paper presented an improved strategy for the passive shimming technology in MRI magnets: measuring the actual magnetic field of multiple representative pieces to correct the calculation; constructing a linear optimization model with the target magnetic field as a variable; adopting “Odd-Even” approach to simplify the assembly of the shim system. Finally, the experiment for the improved shimming technology was performed on a 1.5T MRI superconducting magnet. The results show that the magnetic field homogeneity that meets the imaging requirements could be obtained only through two iterations, and the design value was reached after the third iteration. Compared with the results of the method before improvement, the new shimming strategy has a significant effect.

Magnetic resonance imaging magnet, passive shimming, corrected model, “Odd-Even” approach

10.19595/j.cnki.1000-6753.tces.211698

TM153

科技部重點研發計劃（2019YFC0117604）和江西省自然科學基金（20212BAB214050）資助項目。

2021-10-25

2022-01-14

曲洪一 男，1993年生，助理研究員，研究方向為超導磁體技術。E-mail: quhongyi@mail.iee.ac.cn

王秋良 男，1965年生，教授，博士生導師，研究方向為強電磁科學與技術、應用超導、先進電磁技術與生物醫學交叉。E-mail: qiuliang@mail.iee.ac.cn（通信作者）

（編輯 崔文靜）