具有Bazykin功能反應(yīng)的捕食者-食餌擴(kuò)散模型的穩(wěn)定性

趙明陽(yáng)，孫福芹，劉朋燕

（天津職業(yè)技術(shù)師范大學(xué)理學(xué)院，天津 300222）

眾所周知，生態(tài)系統(tǒng)能夠反映物種與物種間、物種與自然環(huán)境間的相互作用，捕食者-食餌模型作為一類(lèi)經(jīng)典的生態(tài)系統(tǒng)模型，可以用來(lái)研究2個(gè)物種之間的動(dòng)態(tài)相互作用，對(duì)于維護(hù)生態(tài)系統(tǒng)中物種的穩(wěn)定性具有重要意義。在此基礎(chǔ)上，眾多學(xué)者深入分析捕食者-食餌相互作用的特征，構(gòu)建了帶有多種功能性反應(yīng)函數(shù)的捕食者-食餌模型，包括Holling I-III功能反應(yīng)、Holling-Tanner功能反應(yīng)、Beddington-Deangelis功能反應(yīng)以及Ratio-dependent功能反應(yīng)等[1-4]。然而，在對(duì)捕食者-食餌模型的研究中，鮮有文獻(xiàn)考察Bazykin功能反應(yīng)函數(shù)。Bazykin功能反應(yīng)可以描述捕食者飽和的不穩(wěn)定力量與獵物競(jìng)爭(zhēng)的穩(wěn)定力量，這對(duì)于了解種群之間的作用更具實(shí)際意義。另外，現(xiàn)實(shí)世界中的獵物和捕食者總是處于運(yùn)動(dòng)狀態(tài)，為準(zhǔn)確模擬獵物和捕食者的動(dòng)態(tài)特征，需要在模型中考慮種群的空間擴(kuò)散[5-8]。因此，本文構(gòu)建一個(gè)具有Bazykin功能反應(yīng)的捕食者-食餌擴(kuò)散模型，研究模型的有界性和平衡點(diǎn)的存在性，并對(duì)平衡點(diǎn)的局部穩(wěn)定性、全局穩(wěn)定性以及Turing不穩(wěn)定性進(jìn)行分析。

1 模型組成和初步結(jié)果

1.1 模型組成

考慮了一個(gè)具有Bazykin功能反應(yīng)的捕食者-食餌擴(kuò)散模型[9]如下

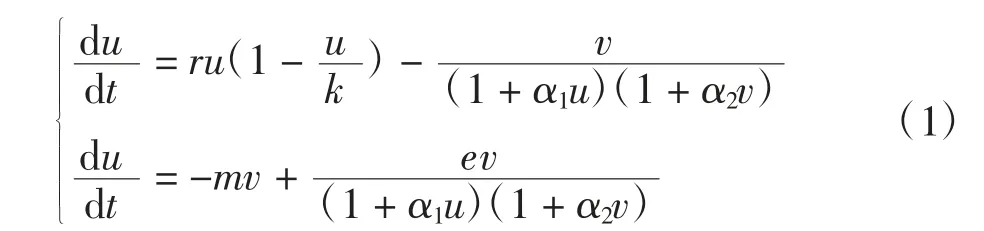
式中：u（t）為t時(shí)刻食餌種群的數(shù)量；v（t）為t時(shí)刻捕食者種群的數(shù)量；增長(zhǎng)率r∈R+；環(huán)境承載力k∈R+；e為食餌到捕食者的轉(zhuǎn)化率（0＜e＜1）；m為捕食者的恒定自然死亡率。

Bazykin型功能性反應(yīng)函數(shù)為f（u，v）=1/（1+α1u）·（1+α2v）。其中，α1和α2為2個(gè)正常數(shù)，且α1＞α2，用來(lái)描述捕食者飽和的破壞穩(wěn)定力和爭(zhēng)奪獵物的穩(wěn)定力。

在現(xiàn)實(shí)世界中，獵物和捕食者始終處于運(yùn)動(dòng)狀態(tài)，該現(xiàn)象可以利用自擴(kuò)散來(lái)模擬。假設(shè)所考慮的2個(gè)種群總是在運(yùn)動(dòng)，每一個(gè)種群都遵循1條路徑，路徑的長(zhǎng)度用x表示。考慮以上假設(shè)，模型（1）可以寫(xiě)為如下形式

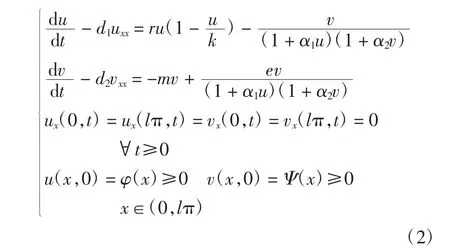
式中：d1、d2分別為食餌和捕食者的擴(kuò)散率；x為捕食者或食餌在時(shí)刻t所在的位置；lπ為所在區(qū)域的范圍。Neuman邊界條件表示食餌和捕食者的移動(dòng)距離為0～lπ。以上所有參數(shù)均為非負(fù)[10]。

1.2 平衡點(diǎn)的存在性

通過(guò)求解du/dt=0，dv/dt=0可以得到模型（2）的平衡點(diǎn)，顯然，模型（2）有平衡點(diǎn)E0（0，0），E1（k，0）以及E2（u*，v*）。u*、v*可根據(jù)方程組（3）求解得出

1.3 有界性

下面給出問(wèn)題（2）解的有界性結(jié)論。

定理1當(dāng)u0（x）≥0，v0（x）≥0且不恒等于0時(shí)，系統(tǒng)（2）有唯一解（u（x），v（x））；當(dāng)t＞0，x∈（0，lπ）時(shí)，0＜u（x，t）＜u*（t）且0＜v（x，t）＜v*（t）。其中，（u*（t），v*（t））為常微分方程（4）的唯一解

進(jìn)一步可以得到

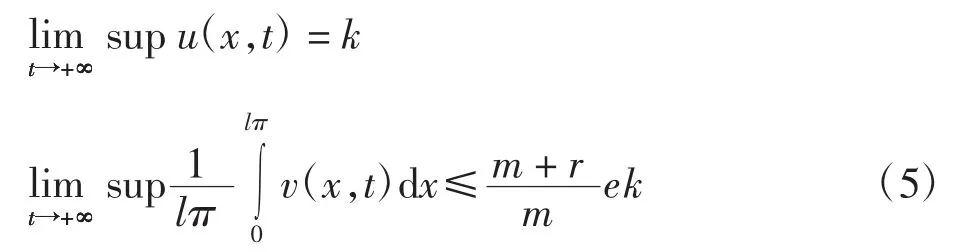
證明令

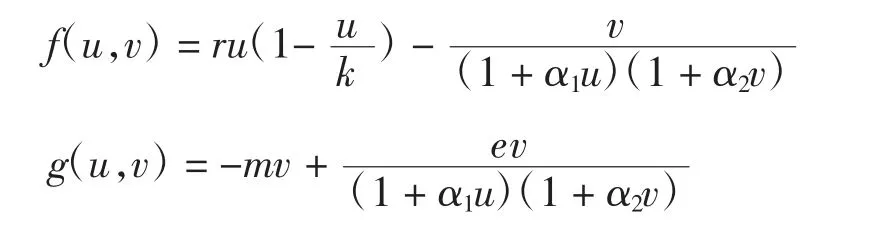
f和g的偏導(dǎo)數(shù)為

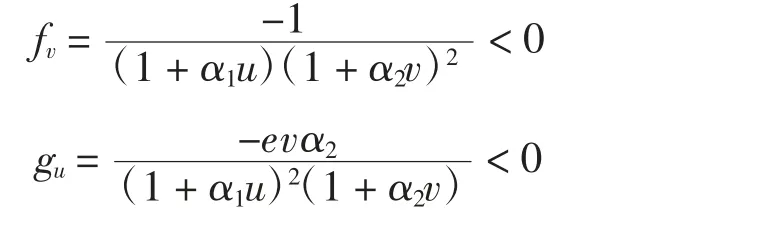
因此，f和g為L(zhǎng)ipschitz函數(shù)，故存在正數(shù)c1、c2對(duì)于u1、u2、v1、v2有

令（u2（x，t），v2（x，t））=（u*（t），v*（t）），滿(mǎn)足方程

令u1（x，t），v1（x，t）=（0，0）滿(mǎn)足方程

其中，0≤u0（x）≤u0*，0≤v0（x）≤v0*，則（u1（x，t），v1（x，t）），（u2（x，t），v2（x，t））分別為系統(tǒng)（2）的上解和下解。強(qiáng)極大值原理表明，當(dāng)t＞0且x∈（0，lπ）時(shí)，u（x，t）＞0，v（x，t）＞0。至此，完成了第一部分的證明。

u（x，t）≤u*（t），v（x，t）≤v*（t），u*（t）為方程ut=ru（x）（1-u（x）/k）的唯一解，且u（0）=u0*＞0。容易證明當(dāng)t→+∞時(shí)，u*（t）→k。所以，對(duì)于?ε＞0，?T0＞0使得u（x，t）≤k+ε。從而得到，當(dāng)t＞T0，x∈（0，lπ）時(shí)，sup u（x，t）=k。

令

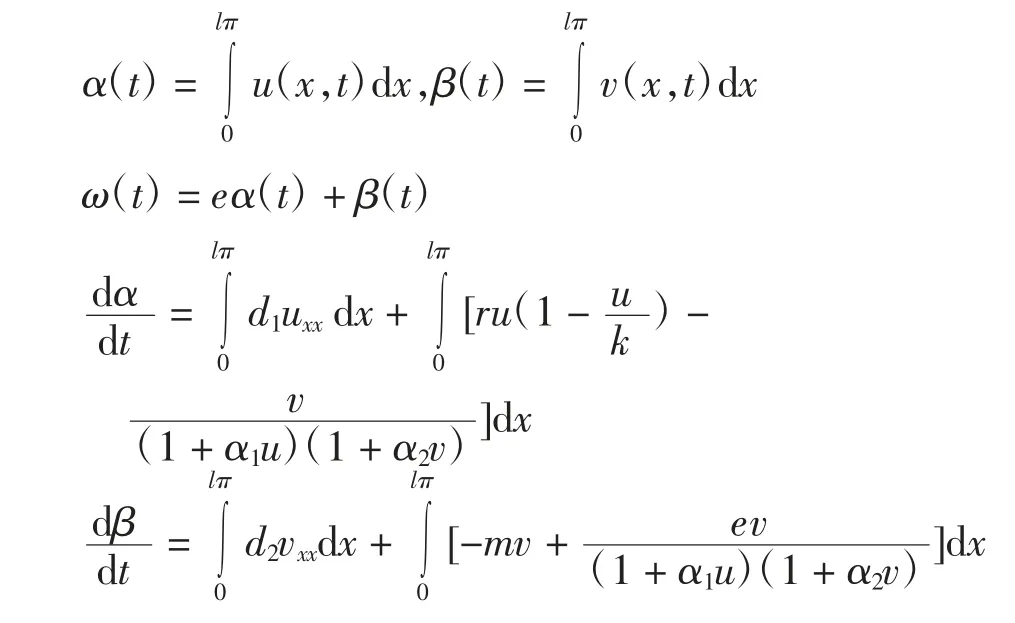
根據(jù)Neumann邊界條件

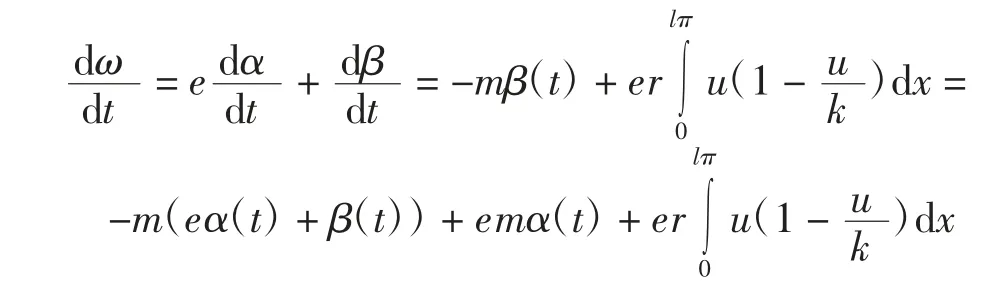
可以得到

得到

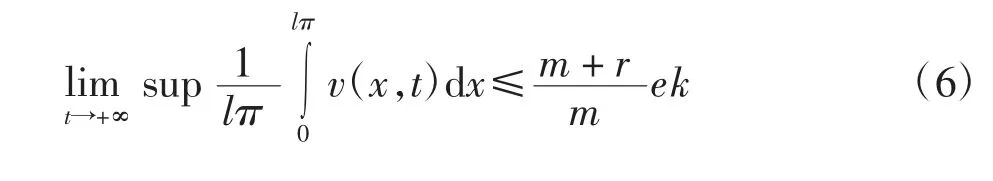
2 穩(wěn)定性分析

系統(tǒng)（2）在任意點(diǎn)（u，v）處的Jacobian矩陣為J=（mij）∈R2×2，

D=diag（d1+d2）及其對(duì)應(yīng)帶有Neumann邊界條件的實(shí)值Sobolev空間可定義為

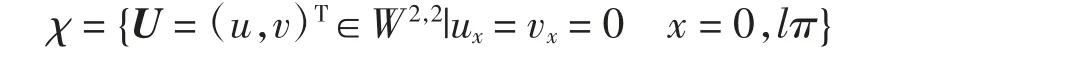
其內(nèi)積為

相關(guān)χ的Hilbertian范數(shù)記為‖·‖2.2，相關(guān)的特征值問(wèn)題為

其中，kn=（n/l）2和cos（nx/l），n=1，2，3…分別為式（7）的特征值和特征函數(shù)。

2.1 E1（k，0）的局部穩(wěn)定性

平衡點(diǎn)E1（k，0）的線(xiàn)性化系統(tǒng)為Ut=DΔU+J（k，0）·U，矩陣-（n/l）2D+J（k，0）的特征值為

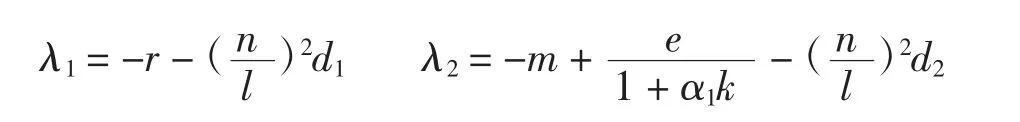
定理2當(dāng)R1=m+e/（1+α1k）＜0時(shí)，系統(tǒng)（2）在平衡點(diǎn)E1（k，0）處是局部漸近穩(wěn)定的。

2.2 E1（k，0）的全局穩(wěn)定性

分別定義系統(tǒng)（2）的上常數(shù)解和下解（u1，v1）=（k+ε，M）和（u2，v2）=（ε，0）。其中，ε、M為正常數(shù)且ε足夠小；定義（）和（），m=1，2，3…為耦合拋物型方程[11]

和

根據(jù)Pao[11]的定理2.1

運(yùn)用比較定理證明方程u（x，t）≤γ（x，t），（x，t）∈[0，lπ]×[0，+∞]，通過(guò)下面的拋物方程

得到t→+∞時(shí)，γ（x，t）→k，在[0，lπ]×[t0，+∞]中，存在t0＞0時(shí)，u（x，t）≤k+ε，這意味著平衡點(diǎn)E1全局吸引，并且定理2證明了在滿(mǎn)足特定條件的情況下，E1局部漸近穩(wěn)定，因此能夠得到E1全局穩(wěn)定。

2.3 E2（u*，v*）的Turing不穩(wěn)定性

系統(tǒng)（2）在正平衡點(diǎn)（u*，v*）處的雅可比矩陣為

系統(tǒng)（2）寫(xiě)成如下形式

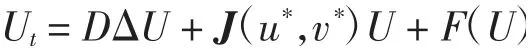
F（U）是圍繞平衡點(diǎn)E2（u*，v*）的非線(xiàn)性函數(shù)。

系統(tǒng)（2）在E2（u*，v*）處的線(xiàn)性化系統(tǒng)為：Ut=DΔU+J（u*，v*）U-（n/l）2D+J（u*，v*）。其中，-（n/l）2D+J（u*，v*）的矩陣為

矩陣（9）的特征值為方程（10）的解

Turing不穩(wěn)定性的存在需要滿(mǎn)足以下2個(gè)方面[12]：

（i）當(dāng)沒(méi)有擴(kuò)散時(shí)，平衡點(diǎn)是線(xiàn)性穩(wěn)定的，D0（k）＞0；

（ii）在擴(kuò)散存在時(shí)，平衡點(diǎn)變得不穩(wěn)定，Dn（k）＜0。

由于

所以

顯然D0（k）＜0，由此可以得到Turing不穩(wěn)定性的不存在性。

3 結(jié)語(yǔ)

本文考慮了齊次Neumann邊界條件下，具有Bazykin功能反應(yīng)的捕食者-食餌擴(kuò)散模型。首先，證明了模型的有界性和平衡點(diǎn)的存在性，得到模型的3個(gè)平衡點(diǎn)E0、E1、E2；其次，證明了在沒(méi)有E2的情況下，E1的局部穩(wěn)定性以及全局穩(wěn)定性；最后，通過(guò)對(duì)平衡點(diǎn)E2（u*，v*）的特征方程進(jìn)行分析，證明Turing不穩(wěn)定性的不存在性。通過(guò)分析具有Bazykin功能反應(yīng)函數(shù)的捕食者-食餌擴(kuò)散模型的穩(wěn)定性，有助于未來(lái)對(duì)具有Bazykin功能反應(yīng)函數(shù)模型的分支問(wèn)題進(jìn)行更深一步的研究。