大跨度斜拉橋時程分析輸入地震波峰值調整方法＊

李曉莉 李小雙

（大連海事大學道路與橋梁工程研究所，遼寧大連 116026）

引言

隨著計算機技術的發展和強震記錄的增加，時程分析法逐漸被推廣應用到結構的動力計算中。時程分析前需要進行地震波的選取，地震波選取的合理性關系到時程分析結果的可靠性。而準確度量地震波強度是合理選擇輸入地震波的基礎，在選取過程中需要對地震波進行峰值調幅，以確保地震波能量與結構所在場地設防烈度相符合。

地震動峰值加速度（PGA）通常由地震波時程曲線中的脈沖波峰所決定。胡聿賢[1]從抗震的觀點出發，認為只有對結構反應有明顯影響的量才是重要的。某些地震波中存在會影響到PGA取值的異常尖峰，假設人為截去這些個別尖峰，PGA會改變，地震波反應譜不會有顯著變化。PGA反映的是地震波本身峰值，與結構和規范反應譜并沒有直接的聯系，用PGA進行峰值調整，可能會對地震能量產生錯誤估計。陳厚群和郭明珠[2]指出，PGA并不是反映地震作用的理想抗震參數，應當用有效峰值加速度（EPA）替代PGA。

PGA與EPA在對地震能量的反映上存在差異。易立新等[3]和鐘菊芳等[4]研究了PGA與EPA的大小比例關系并對影響因素作了探討，發現年超越概率、潛震源與場點的位置、潛震源的分布及潛震源的震級上限大小等多種因素均會對兩種加速度的大小比例產生影響。龍承厚等[5]對PGA、EPA同地震烈度的相關性作了研究，通過對比兩個場地地震加速度記錄數據中的PGA和EPA結果，得出EPA與烈度的相關性較PGA更高的結論。

上述研究發現，基于EPA進行地震波峰值調幅相較PGA而言更為合適，但是實際工程中應用EPA進行峰值調幅的情況較少。地震波峰值調整方法有兩種，分別為基于PGA和基于EPA的調整方法。目前常用的方法是基于PGA的調整方法，即用PGA與《建筑抗震設計規范》（GB 50011—2010）[6]中結構場地地震動峰值加速度進行對比，得到一個調整系數，依據此系數縮放地震波作峰值調幅處理。曹勝濤等[7]、王亞勇[8]和常磊等[9]針對基于EPA的時程分析做了研究，并取得了一些研究成果。基于EPA的峰值調整系數可通過EPA目標值和輸入結構地震波的EPA計算值之比來確定。對于EPA目標值的計算，國內外并沒有通用的定義式。《建筑抗震設計規范》[6]中通過地震影響系數最大值除以放大系數2.25得到；《中國地震動參數區劃圖》（GB 18306—2001）[10]中以地震動峰值加速度按阻尼比5%的標準化地震動加速度反應譜最大值的1/2.5倍確定；美國ATC-3《結構抗震設計樣本規范》[11]中按阻尼比5%的地震動加速度反應譜中周期0.1—0.5 s間平均反應譜值除以該周期范圍內的平均動力放大系數2.5計算；美國地震危險區劃圖[12]中，將其取為阻尼比5%的地震動加速度反應譜中周期0.2 s所對應的反應譜值除以該周期范圍內的平均動力放大系數2.5。對于EPA計算值，曹勝濤等[7]提出了按地震動記錄的類型區分加速度型、速度型和位移型的EPA計算公式；安東亞[13]提出了不需對地震波進行分類的、可適用于所有類型地震波的EPA計算公式。

基于EPA的地震波峰值調整研究總體偏少，常磊等[9]通過平滑后的地震波反應譜計算EPA，但是對平滑方法的相關參數和效果并未作出研究和評價；安東亞[13]計算EPA時通過原地震波反應譜取相關參數，并未對其作平滑處理。由于EPA目標值依據的規范譜是大量譜平均、平滑得到的，所以EPA值的得出也應當基于平滑后的反應譜。此外，相關研究應用對象大部分針對建筑結構，橋梁結構的研究較少。本文中基于EPA的地震波峰值調整方法研究應用對象為大跨度斜拉橋，考慮建筑結構與橋梁結構之間的差異和EPA相關計算系數的選取，探究現有EPA調整方法中存在的不足，提出一種適用于大跨度斜拉橋結構的EPA峰值調整方法，進而獲得更加可靠的地震反應結果。

1 基于EPA的大跨度斜拉橋地震波選取研究

1.1 大跨度斜拉橋結構EPA計算方法

橋梁結構與一般的建筑結構有所差異，基礎深、跨度大等特點使得橋梁抗震規范中設計反應譜與建筑抗震規范不同。依據《公路橋梁抗震設計規范》（JTG/T 2231-01—2020）[14]5.2.1節設計加速度反應譜條文說明，主要不同集中在以下兩點：

（1）《公路橋梁抗震設計規范》[14]中5.2.1條文說明提到，一項專題研究根據模擬和數字記錄反應譜長周期段特征的比較，論證了設計反應譜周期范圍可以擴展到10 s（建筑規范中為6 s）；

（2）考慮到我國經濟實力提升，抗震設防要求也隨之提升，計算基本地震動峰值加速度中的常數值由2.25改為2.5，相當于全面提高了抗震設防標準（建筑規范中為2.25）。

基于以上兩點和現有的EPA計算公式，大跨度斜拉橋的EPA計算公式可定義為：

人工合成地震波EPA計算公式：

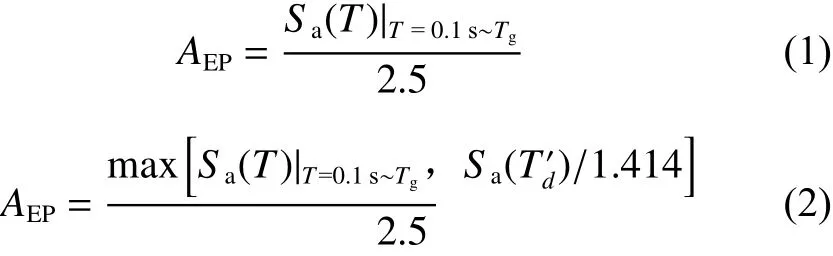
天然地震波EPA計算公式：

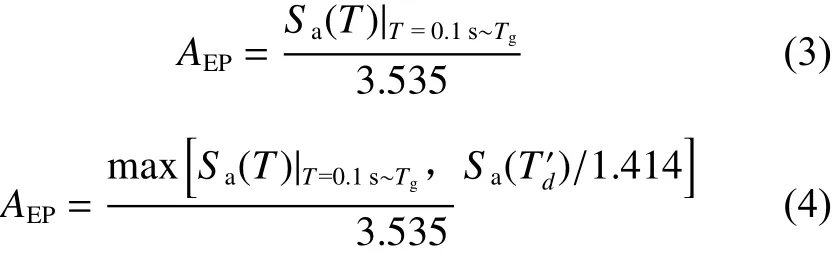
EPA目標值計算公式：

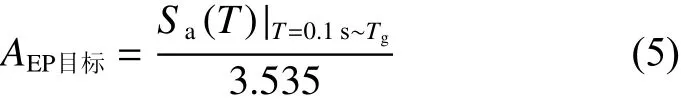
式中，AEP目標為目標EPA值，即需要縮放到該數值的規范地震動峰值加速度數值，Tg是特征周期，為對應周期段反應譜均值，為全周期范圍內反應譜峰值，3.535為2.5和1.414的乘積（考慮天然波反應譜的波動性比人工波更大，計算時在原有數值上除以1.414）。當平臺范圍外無較大峰值，按式（1）、（2）計算EPA，否則按式（3）、（4）計算。

需要注意的是，目前EPA調整方法僅適用于水平向地震動，在豎向地震動的應用上還存在著不足，所以豎向地震動的峰值調整仍采用基于PGA的方法。

1.2 基于EPA的峰值調整方法研究

地震波的選取研究，包括地震波的初選和峰值調幅兩部分，本文研究重心在峰值調整上。基于EPA的峰值調整方法，并非是直接將選取的天然地震波轉換成反應譜，再計算出EPA值進行調整峰值。由于規范中的場地設計反應譜，是經過大量地震動記錄統計、平均處理得到的，所以計算EPA前應該將地震波反應譜作平滑處理。

常磊等[9]對地震波反應譜采取了一種較為簡單的跟隨平均處理，這種處理實際上是一種圖像去噪手段，即均值處理[15]。將地震波反應譜視為 “圖像” ，不規則的曲線視為 “噪聲” ，反應譜的平滑處理可以視為圖像去噪的過程。應用該領域的手段進行地震波反應譜平滑處理研究，探究平滑效果。

1.2.1 平滑處理研究

1.2.1.1 均值平滑處理

均值平滑處理是典型的線性算法，對于地震波反應譜上的目標周期點，取一個區間，該區間包括了其周圍的鄰近點，再用區間中的全體點（除該點）的平均值來代替原來目標點值。計算表達式為：

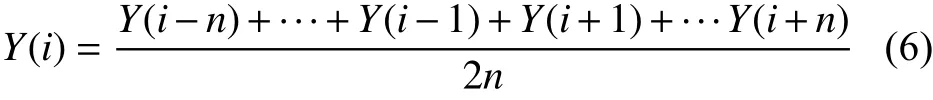
式中，n為目標周期點左右區間（鄰域）點的個數，若周期點鄰域數據的個數不足n個，則按照端點數據值補足。

1.2.1.2 加權均值平滑處理

對均值平滑處理采取加權手段。先取出目標周期點i鄰域內2n個點（目標點除外，鄰域點編號為j），對這2n個點計算均值，再用每一點的反應譜值與均值作差，該差值的絕對值與所有差值的絕對值之比即為權重，權重和對應點譜值的乘積之和即為目標點平滑譜數值。計算表達式為：

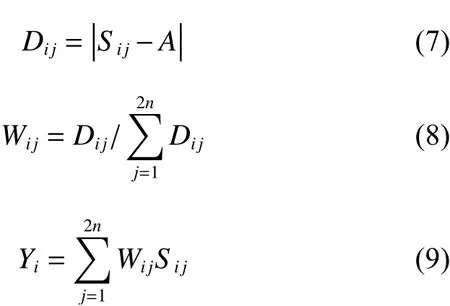
式中，Sij為鄰域內每一點對應反應譜值，A為均值，Di j為 鄰域內每點反應譜值與均值之差的絕對值，Wij為權重，Yi為目標點平滑譜值。

1.2.1.3 規范反應譜平滑處理

將平滑曲線向規范反應譜過渡的處理手段，這里需要用到兩種反應譜，一種是地震波反應譜，另一種是規范反應譜。先取出目標周期點i鄰域內2n個點（目標點除外，鄰域點編號為j），每一點對應的地震波反應譜值與規范設計反應譜值作差，該差值的絕對值與所有差值的絕對值之比即為權重，權重和對應點地震波反應譜值的乘積之和即為目標點平滑譜數值。計算表達式為：

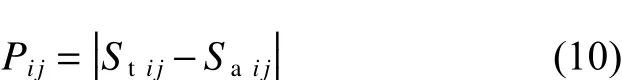
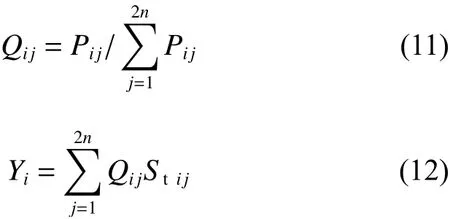
式中，Stij為鄰域內每一點對應地震波反應譜值，Saij為鄰域內每一點對應規范設計反應譜值，Pij為反應譜與規范譜之差的絕對值，Qij為 權重，Yi為目標點平滑譜值。

1.2.2 鄰域區間研究

上述平滑方法需要研討鄰域的取值范圍，鄰域過大，會導致反應譜峰值段明顯降低，計算得出的EPA不夠準確；鄰域過小，平滑后的反應譜形狀接近原反應譜，達不到理想效果。嘗試建立一個系數，使其適用大部分地震波反應譜的平滑處理，滿足條件即認為鄰域合理。該系數建立的設想是：選取若干條地震波，將其轉換成反應譜后作平滑處理。將平滑譜最大峰值段某一小區間內數據的均值與原地震波反應譜最大峰值段某一小區間內數據的均值做比，統計該比值落在各區間的比例（如0.5—0.6占比）。若落在某一區間的百分比重明顯大于其他區間，則可以利用該區間的端點值反算出鄰域區間。此鄰域區間內的平滑處理曲線可視為滿足平滑要求。

在美國太平洋地震波庫中，依托抗震設防烈度為8度的某大跨度斜拉橋場地條件計算設計反應譜作為規范譜，按照不同震級、震中距等條件選取了400條地震波記錄進行系數的探討研究。

先使用Seismo Signal軟件將地震波轉換成反應譜，再用Matlab編譯出3種平滑處理方法，用循環處理各個反應譜數據得出系數，將數據統計后制成表1。

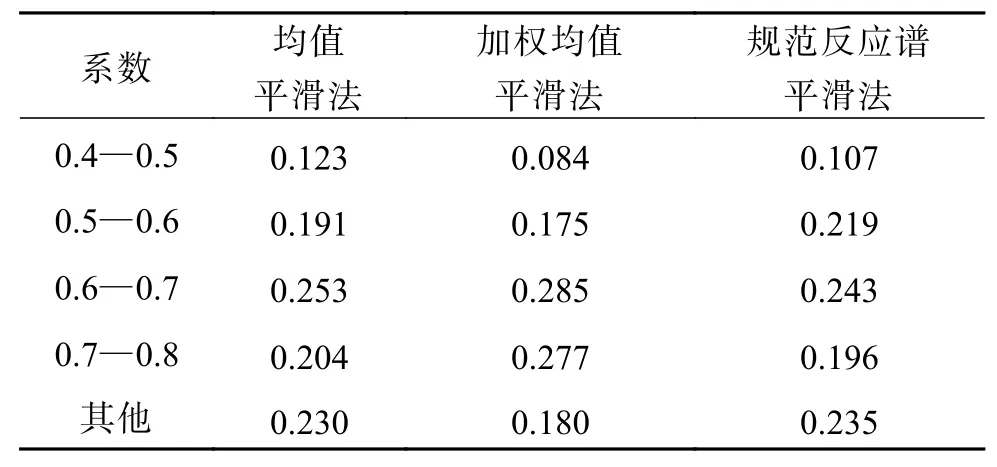
表 1 鄰域系數比例分布Table 1 Proportional distribution of neighborhood coefficient

由表1數據可見，匯總后的系數所占百分比仍然沒有足夠的比重進行建立。不同條件下地震波所轉換的反應譜差異性較大，使得平滑后反應譜與原反應譜最值處的比值很難構建出統一的系數關系。由于反應譜在波峰段的變化很大，所以地震波平滑譜峰值與原反應譜峰值之比只適合對于該條地震波做研究推導，而不具有普適性，想依托其反算鄰域區間的取值范圍具有較大的隨機性。因此，鄰域區間的取值很難確定一個概念上的適用區間，需要針對目標反應譜單獨調整，取得合適的數值。

1.2.3 平滑效果對比分析

以地震波記錄Kern County和Managua，Nicaragua-02為例，采用以上3種方法進行處理，對比結果尋找最優的平滑方法。所選兩條地震波的時程曲線如圖1和圖2所示。

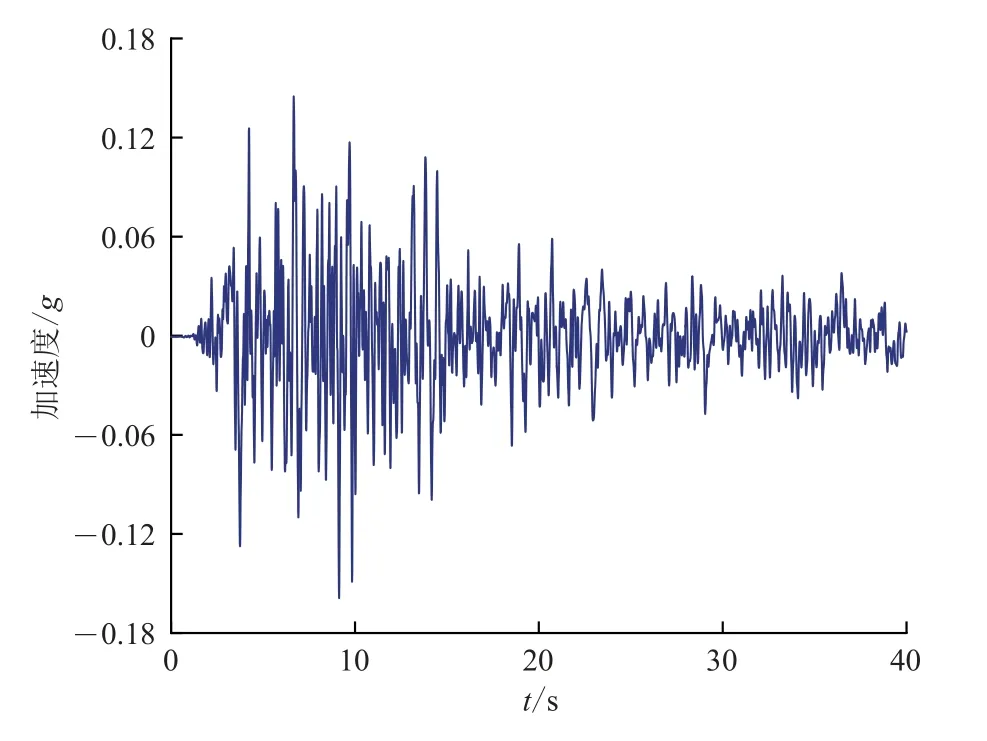
圖 1 地震波Kern County加速度時程Fig. 1 Acceleration time history of seismic wave Kern County

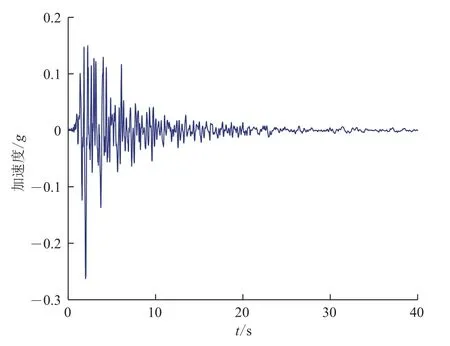
圖 2 地震波Managua，Nicaragua-02加速度時程Fig. 2 Acceleration time history of seismic wave Managua，Nicaragua-02

應用Seismo Signal軟件對地震波記錄濾波后，轉換出地震波反應譜數據導入Matlab軟件中，根據上述3種方法作平滑處理。平滑處理后的反應譜與初始反應譜對比分別如圖3和圖4所示。

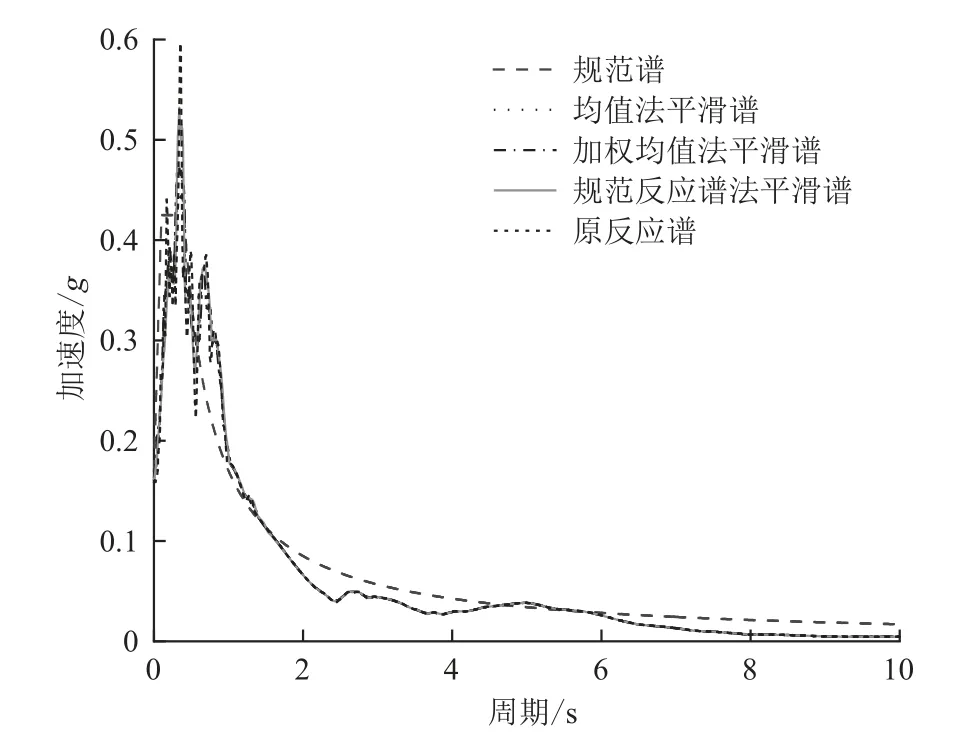
圖 3 地震波Kern County加速度譜平滑前后對比Fig. 3 Comparison of seismic wave Kern County acceleration spectrum before and after smoothing

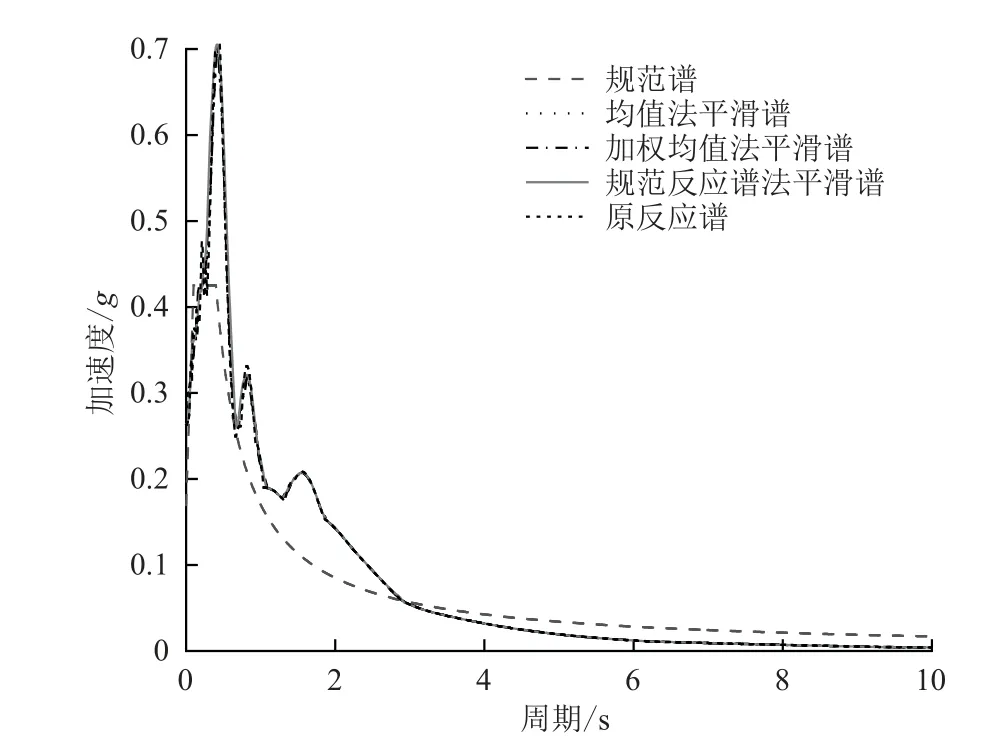
圖 4 地震波Managua，Nicaragua-02加速度譜平滑前后對比Fig. 4 Comparison of seismic wave Managua，Nicaragua-02 acceleration spectrum before and after smoothing

在相同鄰域下，3種平滑方法在1—10 s周期段內的平滑曲線趨于一致，主要不同集中在0—1 s周期范圍內。平滑后的反應譜（簡稱平滑譜）評判指標有兩個，一個是平滑度，另一個是對反應譜的特征反應程度。

針對平滑度的比較，引入變異系數的概念[16]。變異系數也稱離散系數，是反映數據分布狀況的指標，計算上為總體各單位的標準差與平均值的比值。在圖像處理中，用變異系數的倒數（平滑指數）來反映濾波算法對圖像噪聲的平滑作用，取值范圍為 0—1，其值為濾波后圖像的均值與濾波后圖像的標準差的比值。將之應用在地震波反應譜圖像的平滑評價中，可反映平滑譜的平滑度，平滑指數越小，平滑譜的平滑度越高。

經計算，圖3的均值法平滑譜、加權均值法平滑譜、規范反應譜法平滑譜的平滑指數分別為0.659、0.654和0.652，圖4中3個平滑指數分別為0.619、0.620和0.609。依據圖像曲線特征，均值平滑法反應譜較為光滑平整，在一定程度上保留了反應譜的特征；加權均值平滑法是對均值平滑處理方法作加權處理，引入權重調整平滑譜的地震影響系數分布，在平滑度上，隨著地震波記錄的不同與均值平滑法各有優劣，但是在邏輯考慮上更為嚴謹；規范反應譜平滑法在平滑度上優于上述兩種方法，且在反應譜的特征反映上更為顯著。由于地震波是根據結構規范設計反應譜選取的，且規范譜反映了結構所在場地的地震參數，所以依托規范譜作為權重進行的平滑處理方法，在理論上比前兩種單純采用數學手段的處理方法更具有說服力。

通過大量地震波記錄的平滑處理數據，發現當地震波反應譜形狀復雜時，規范反應譜法平滑法的平滑度與前兩種方法相比稍顯不足，但相差不大，三者平滑指數的差值在0.1范圍內；而在對反應譜的特征反應程度上，規范反應譜法平滑法明顯優于前兩種方法。因此，在采用兩個指標綜合評定后，建議采用規范反應譜法進行地震波反應譜的平滑處理。

2 應用實例

以港珠澳大橋青州航道橋為工程背景，依據橋址處場地條件和地震分組，在美國太平洋地震波庫中選取3組天然波記錄（San Fernando，Chalfant Valley-02，Westmorland），對3組記錄分別作基于PGA和基于EPA的峰值調整處理，輸入有限元模型中進行時程分析，比對分析結果。

2.1 模型建立

港珠澳大橋青州航道橋為主跨458 m的雙塔斜拉橋，采用半漂浮體系，橋跨組合為110 m+236 m+458 m+236 m+110 m。橋型布置如圖5所示。

采用Midas/Civil建立港珠澳大橋青州航道橋有限元模型，主梁應用脊梁模式，采用Q345鋼材，以三維梁單元模擬；橋塔和橋墩采用C50混凝土，均以三維梁單元模擬；拉索雙索面對稱布置，以桁架單元模擬。有限元模型如圖6所示。

圖 5 青州航道橋橋型布置Fig. 5 Bridge type layout of Qingzhou Channel Bridge

圖 6 全橋有限元模型Fig. 6 Finite element model of whole bridge

2.2 反應譜分析

根據青州航道橋地質條件和《公路橋梁抗震設計規范》[14]中橋梁設計加速度反應譜（規范譜）計算公式，計算出E1地震作用下的規范譜，應用到有限元模型中進行反應譜分析。將E1地震作用下的反應譜法結果和線性時程分析結果對比校核，經校核，線性時程分析結果總體滿足規范要求大于反應譜法80%的要求。

2.3 峰值調整

將上述3組地震波記錄簡稱為地震波-S、地震波-C和地震波-W，在E1、E2地震作用下，常規PGA直接調幅和平滑后計算EPA調幅，兩種手段的峰值調整系數如表2所示。

2.4 線性時程分析

將3組地震波分別按兩種調整方法在E1地震作用下的峰值調整系數進行調整，調整后的地震波分別按順橋向、橫橋向和豎向輸入，輸入比例依據《建筑抗震設計規范》[1]中規定為x∶y∶z=1∶0.85∶0.65。對橋梁模型進行線性時程分析。

選取大跨度斜拉橋結構6個關鍵截面來對比線性時程分析結果，包含輔助墩處截面、次邊跨跨中截面、主塔處截面、中跨跨中截面4個主梁關鍵截面，橋塔塔頂截面和橋塔塔底截面2個橋塔關鍵截面，編號1-1至6-6。根據《公路橋梁抗震設計規范》[14]相關規定，當采用3條地震波進行時程分析時，結果取其中的最大值，分析結果如表3和表4所示。

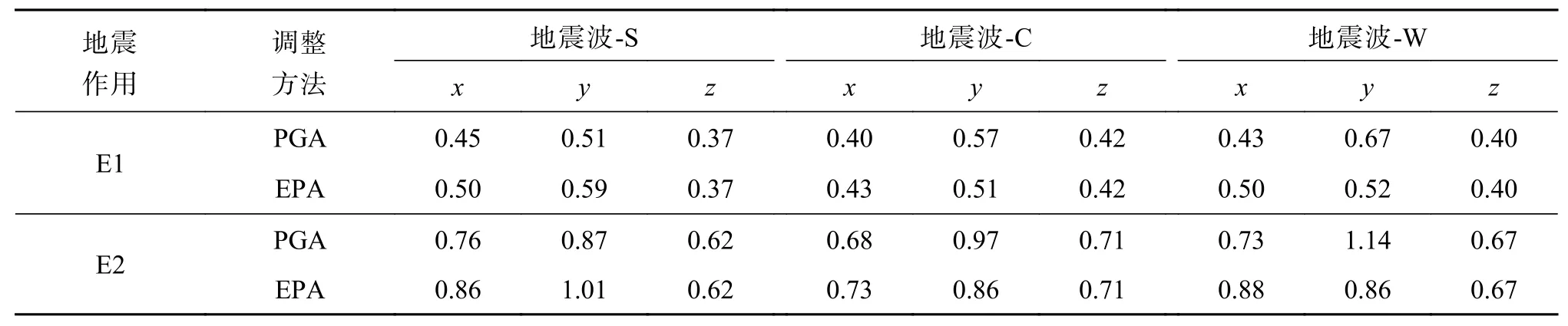
表 2 峰值調整系數Table 2 Peak adjustment factor

將線性時程分析結果與反應譜法結果作比對。本應列出反應譜法在兩種調幅方法下位移、內力結果表格以及時程分析與反應譜法位移、內力結果對比表格，限于篇幅，將上述時程分析在兩種調幅方法下的位移、內力結果與反應譜法結果對比，以相對比值分析對比結果，如表5和表6所示。

由表3可知，基于不同調整方法的兩組時程分析，位移最大值變化基本符合峰值調整系數總體趨勢，即x向調整系數EPA方法較大，y向調整系數PGA方法較大。

由表4可知，基于EPA的時程分析內力最大值總體高于基于PGA的數值，且兩者之間沒有數量級的差異。

由表5和表6可知，兩種調整方法得出的時程結果具有一定能量差異。從總體表征上看，基于EPA的地震波時程結果的離散性較PGA有所降低，說明基于EPA的地震波調整方法對地震波的能量預估更加全面，依托此方法對大跨度橋梁結構進行抗震分析具有可行性。

2.5 非線性時程分析

對橋梁模型定義塑性鉸和非線性邊界，將3組地震波分別按兩種調整方法在E2地震作用下的峰值調整系數進行調整，調整后的地震波分別按順橋向、橫橋向和豎向輸入，輸入比例為x∶y∶z=1∶0.85∶0.65。對橋梁模型進行非線性時程分析。

關鍵截面選取與線性時程分析相同截面，時程分析結果的最大值如表7和表8所示。

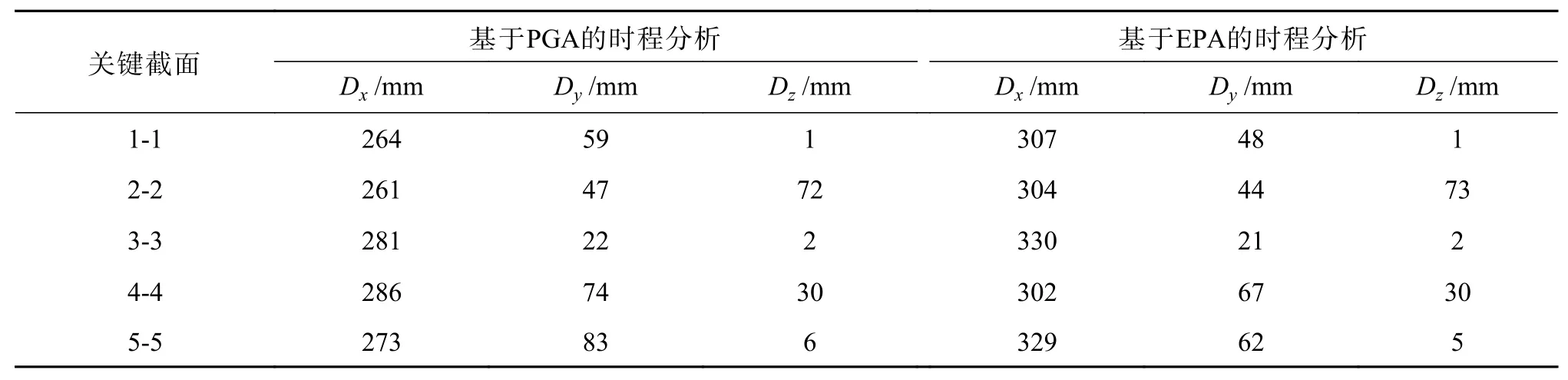
表 3 線性時程分析位移峰值Table 3 Peak displacement of linear time history analysis

表 4 線性時程分析內力峰值Table 4 Peak internal force of linear time history analysis

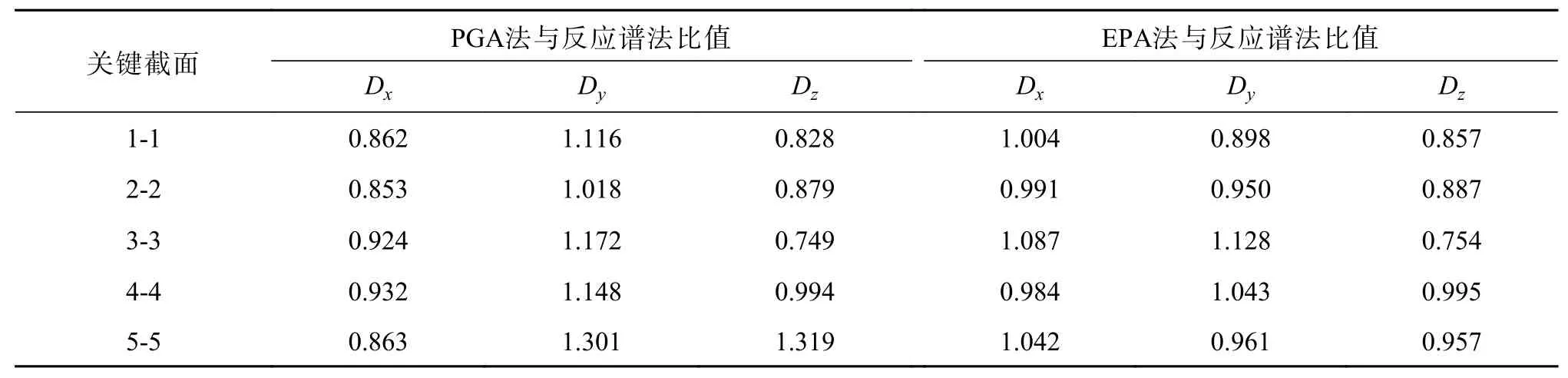
表 5 線性時程分析與反應譜法位移比值Table 5 Displacement ratio of linear time history analysis and response spectrum method

由表7可知，基于不同調整方法的兩組非線性時程分析結果位移最大值變化規律和線性時程分析結果近似，基本符合峰值調整系數總體趨勢，即x向調整系數EPA方法較大，y向調整系數PGA方法較大。

由表8可知，在非線性時程分析下，基于EPA調整方法的內力最大值總體高于基于PGA方法的數值，且兩者之間并未有數量級的差異。

綜上所述，非線性時程分析下兩種調整方法的動力響應結果存在能量上的差異，總體表征上與線性時程分析相似。應用基于EPA的峰值調整方法相較基于PGA的方法，更加全面地反映了地震能量，對大跨度斜拉橋的地震波調整具有一定的優化效果。

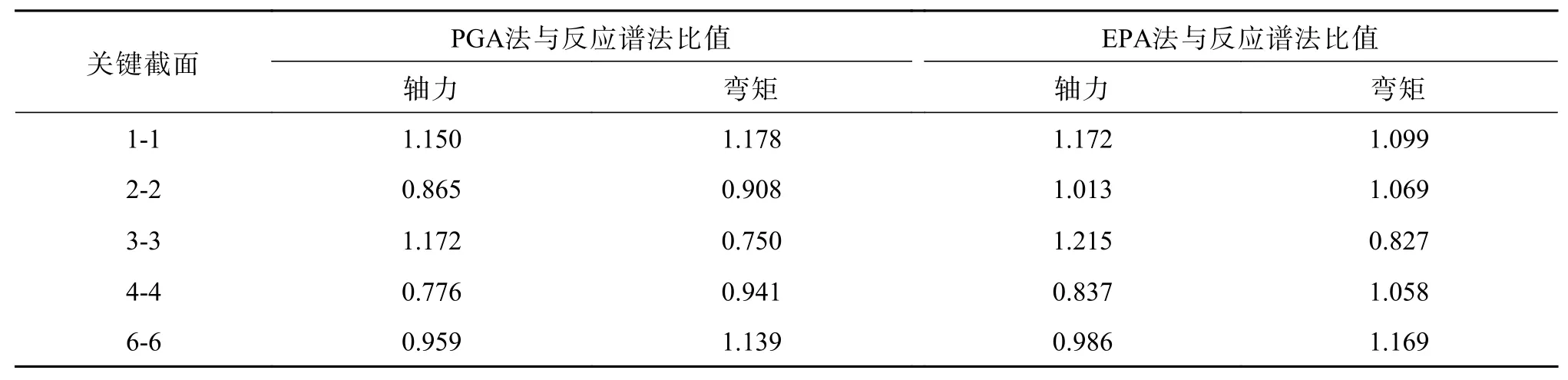
表 6 線性時程分析與反應譜法內力比值Table 6 Internal force ratio of linear time history analysis and response spectrum method

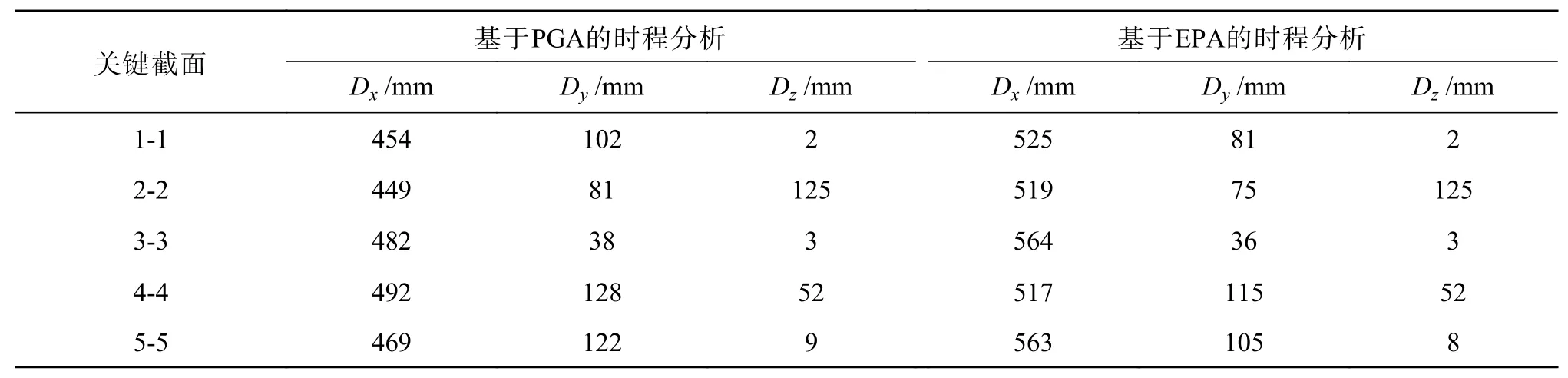
表 7 非線性時程分析位移峰值Table 7 Peak displacement of nonlinear time history analysis

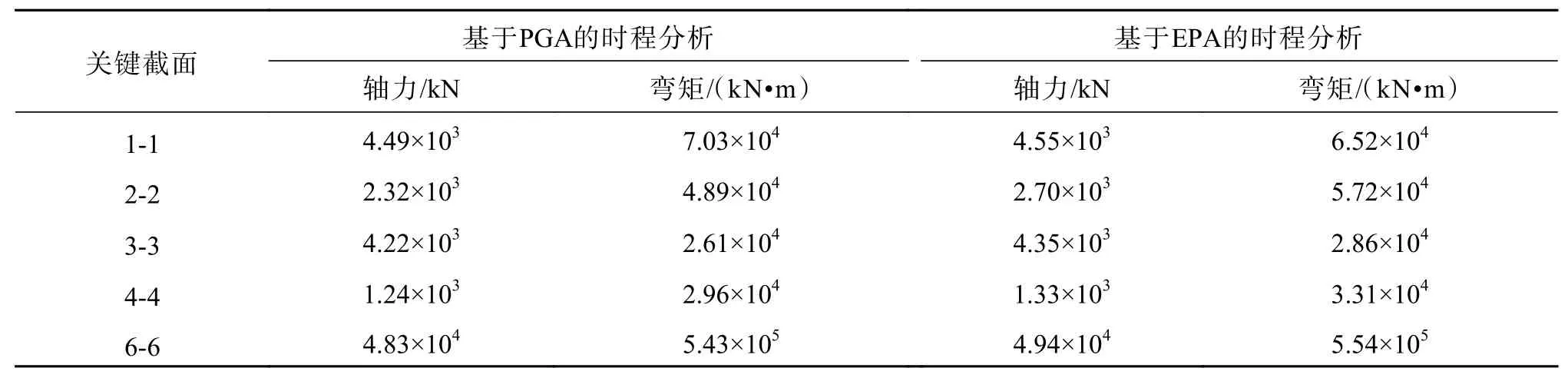
表 8 非線性時程分析內力峰值Table 8 Peak internal force of nonlinear time history analysis

3 結論

（1）基于PGA的調整方法雖然簡單，但是PGA與規范譜及結構沒有直接聯系，不能較好地反映地震能量，與設防烈度之間的關系存在較大的離散性。

（2）提出將基于EPA的峰值調整方法應用于大跨度斜拉橋的時程分析。根據建筑結構已有的EPA計算公式和橋梁規范，針對建筑與橋梁結構的不同特點，對相關參數作改進，使其適用于大跨度斜拉橋結構EPA的計算。

（3）對地震波反應譜的平滑作探討，討論了相關參數的取值和各種方法的平滑效果。經過平滑度、反應譜的特征反應程度兩個指標的篩選，建議使用規范反應譜法進行平滑處理。此方法可以在保證平滑效果的同時，也能較好地反應地震波反應譜的特性。

（4）通過算例初步驗證了基于EPA的地震波峰值調整方法應用于大跨度斜拉橋的可行性。但是，該調整只適用于水平向地震波，豎向地震波仍采用基于PGA的調整方法，對豎向地震波的EPA調整需要做進一步研究。