飽和狀態下黃綿土坡面細溝侵蝕可蝕性和臨界剪切應力特征

黃鈺涵，楊夢格，雷廷武，李法虎，王 偉

飽和狀態下黃綿土坡面細溝侵蝕可蝕性和臨界剪切應力特征

黃鈺涵1,2，楊夢格2，雷廷武1※，李法虎1，王 偉3

（1. 中國農業大學水利與土木工程學院，北京 100083；2. 廣西大學林學院，廣西森林生態與保育重點實驗室，南寧 530004；3. 中國農業大學工學院，北京 100083）

土壤可蝕性參數和臨界剪切應力是評價土壤易侵蝕程度和抗水流剪切變形能力的重要指標，目前在黃綿土坡面細溝侵蝕過程中，土壤飽和條件下可蝕性參數和臨界剪切應力的變化尚不明確。該研究采用室內土槽模擬沖刷試驗確定不同坡度（5°、10°、15°、20°）和流量（2、4、8 L/min）下飽和黃綿土坡面的最大細溝剝蝕率，基于數值法、修正數值法和解析法計算土壤可蝕性參數和臨界剪切應力。結果表明，3種方法所得最大細溝剝蝕率均隨坡度和流量增加而增大，其中修正數值法和解析法計算的最大細溝剝蝕率更接近。土壤可蝕性參數分別是0.470、0.278和0.256 s/m，土壤臨界剪切應力分別為1.502、1.306和1.367 N/m2。修正數值法可提高數值法近似計算的精度，使近似計算結果更接近解析法計算獲得的理論值。飽和較未飽和黃綿土的土壤可蝕性參數略有減小（16.83%），而臨界剪切應力減小了66.97%，表明土壤飽和對黃綿土土壤可蝕性參數影響很小，但大幅度削弱了土壤臨界剪切應力，使得黃綿土坡面飽和后土壤侵蝕更為強烈。此外，飽和黃綿土邊坡的臨界剪切應力與飽和紫色土坡面相比差異不大，而細溝可蝕性參數大2.26倍，表明土壤飽和對2種土壤臨界剪切應力影響程度相似，但黃綿土較紫色土對土壤侵蝕的敏感性更高。研究結果可為飽和狀態下不同土壤坡面細溝侵蝕模型參數的優化提供參考。

土壤；侵蝕；細溝；可蝕性；臨界剪切應力；飽和；最大細溝剝蝕率

0 引 言

細溝侵蝕是坡面侵蝕泥沙的重要來源，是坡面侵蝕泥沙運移的主要通道。侵蝕細溝形成后，土壤侵蝕顯著增加，土地退化加劇，嚴重威脅農業可持續發展[1-3]，因此，研究者們對土壤侵蝕預報和土壤侵蝕控制措施持續關注[4]。目前，常用的土壤侵蝕預報模型包括：經驗模型（Universal Soil Loss Equation (USLW)和Revised Universal Soil Loss Equation (RUSLE)）、基于物理過程的預報模型（Water Erosion Prediction Project (WEPP)和European Soil Erosion Model (EUROSEM)）、分布式流域水文模型（Soil and Water Assessment Tool (SWAT)）等[5-6]。土壤可蝕性參數和臨界剪切應力是土壤侵蝕預報模型的2個重要參數，其中，土壤可蝕性是指土壤是否易受侵蝕破壞的性能, 即土壤對侵蝕介質剝蝕和搬運的敏感性[7]；土壤的臨界剪切應力是表征土體力學性質的一個主要指標，它的大小與土壤凝聚力和內摩擦角有關，可直接反映土體抵抗外力作用發生剪切變形破壞的能力[7]。因此，這2個參數是評價土壤易侵蝕程度和抗水流剪切變形能力的重要指標[8-9]。

土壤可蝕性參數與臨界剪切應力作為土壤坡面細溝侵蝕模型的重要參數，實現其精確計算對提高細溝侵蝕模型精度有十分重要的意義。研究發現影響土壤可蝕性參數和臨界剪切應力的因素包括：土壤含水量[10-12]、土壤水勢梯度[13]、有機質含量[14]、坡度、水流流量[7]、土壤孔隙水壓力[13,15-16]、土壤孔隙比[17]等。其中，土壤含水量的影響越來越受到關注，Hanson等[10]發現土壤抗侵蝕能力隨著土壤含水量的增加在土壤塑限范圍內升高。Su等[15]發現隨著土壤水文條件的變化（從排水到飽和再到滲流狀態下），不同土壤類型（黃褐土、紫色土、干紅壤）的土壤可蝕性參數逐漸增加，而臨界剪切應力沒有顯著變化。Nouwakpo等[13]發現土壤滲流狀態下臨界剪切應力隨垂直水力梯度的增加呈線性減小趨勢，導致土壤侵蝕加劇。邢行等[12]通過限定性細溝模擬試驗指出，土壤水分含量變化會引起土壤臨界剪切應力的變化，這與Singh等[11]研究小流域土壤侵蝕得出的試驗結果一致。以上研究均表明土壤含水量不同能引起近地表水文狀況顯著變化，進而引發不同程度的土壤侵蝕。土壤飽和作為一種特殊的近地表水文狀況，顯著影響了土壤團聚體結構、土壤孔隙水壓力和表面粗糙程度等[18]，進而改變土壤侵蝕。目前關于土壤飽和的研究主要集中于坡面產流產沙過程[19-22]及土壤力學性質方面[23-25]，而針對飽和土壤坡面土壤可蝕性參數和臨界剪切應力的研究較少，開展相關研究可為完善土壤侵蝕預報模型提供科學依據。

黃土高原地區每年60%～70%的降雨量集中于夏季，降雨具有短歷時、高強度的特點[26]。極端降雨條件下，可能因犁底層入滲受阻，使耕層逐漸形成飽和土層，加劇土壤流失。黃綿土作為黃土高原分布面積最大的土壤類型，是受強降雨影響形成農地耕作層飽和土壤侵蝕的核心區域之一，因此針對黃土區坡耕地飽和狀態下黃綿土邊坡的土壤侵蝕研究顯得尤為重要。本文研究黃綿土坡面飽和對土壤可蝕性參數和臨界剪切應力的影響，并對比了黃綿土與紫色土的差異，以期為飽和狀態下土壤坡面細溝侵蝕模型參數的優化提供科學基礎。本文主要研究內容如下：1）根據室內試驗細溝剝蝕率數據集，運用數值法、修正數值法和解析法計算飽和黃綿土的細溝可蝕性參數和臨界剪切應力；2）根據解析法精確計算的理論值，明確數值法與修正數值法的計算精度；3）對比飽和與未飽和狀態下黃綿土坡面及飽和狀態下黃綿土與紫色土的土壤可蝕性參數與臨界剪切應力。

1 材料與方法

1.1 供試土壤

試驗土壤為黃綿土，采集自中國科學院水利部水土保持研究所安塞水土保持綜合試驗站（36°51′30″N、109°19′23″E）周邊的退耕荒地，該區域為典型梁茆狀黃土丘陵溝壑區。將收集的土壤風干后過4 mm篩，使用Mastersizer 3000激光粒度分析儀（Malvern, UK, ±1%）測定試驗土壤機械組成結果如下：砂粒、粉粒和黏粒體積分數分別為23.80%、64.57%和11.63%，根據美國制土壤質地分類標準試驗土壤為粉壤土。通過重鉻酸鉀法測得有機質含量為4.5 g/kg。

1.2 試驗設計與數據集

試驗在中國農業大學水利與土木工程學院模擬降雨大廳進行，試驗土槽為鋼制可調節坡度土槽，長8 m、寬1.2 m。用鋼板將土槽中間隔成8個8 m×0.1 m×0.35 m的限定性溝槽，即8條細溝，每條細溝長度為8 m，寬度0.1 m，深度0.25 m。在最左和最右側預留出0.2 m設置飽和土壤裝置，隔板間及隔板與試驗平臺的間隙用黏質土壤填充壓實5 cm厚，用于模擬犁底層，填土容重為1.5 g/cm3。

供試土槽的8條細溝以1 m為間隔等分為8條溝段,每米溝段的底部都壓實填充3 cm厚的黏土層，并在每米溝段的黏土層上方水平設置1根水管，每根水管位于每米溝段前端10 cm處，且貫穿8條細溝（圖1a）。每個0.1 m溝段間隔的滲水管上表面布設3個滲水孔（直徑2 mm），滲水孔的間距為20 mm，在安裝時滲水孔朝上坡方向放置。自滲水管向下游0.9 m長都用黏性土壤填充壓實2 cm，土壤容重為1.5 g/cm3，每米溝段的前部0.1 m采用粗砂填充2 cm并覆蓋滲水管，作為滲水單元向供試土壤中供水（圖1b）。滲水管上部為供水管，每個供水管上安裝閥門控制供水水量，8根供水管末端都共同連接至1根輸水管，將水流分別輸送至各供水管。此外，在8條細溝中均鋪設滲水良好的土工織物以保護底部沙層，填入20 cm厚的供試土壤并自然沉降。

圖1 試驗裝置圖

試驗工作原理為水流通過輸水管進入供水管而后到達滲水管，并通過滲流孔進入沙層直至沙層達到飽和，而后水流持續向上飽和供試土壤，并逐漸向下游推進，最終實現全坡面土壤供水直至完全飽和。根據中國農耕地的坡度最高25°，且據已有研究[27]以及野外坡耕地調研，細溝發育的臨界坡度為2°，且在5°以上發育最為廣泛，因此試驗選取緩斜坡、斜坡與陡坡的代表性坡度，設置4個坡度：5°、10°、15°、20°。根據以往研究[28]得出的黃綿土坡耕地產生細溝侵蝕的臨界流量及黃綿土細溝侵蝕研究中采用的人工模擬降雨強度進行換算，同時為了與前人研究[4]體系保證統一以便對比，因此，本文設計3個流量：2、4、8 L/min。當供試土壤完全飽和后，調節坡度與流量測定細溝侵蝕水流流速與沿程含沙水樣濃度，且試驗開始前供水條件保持不變。采用電解質示蹤法測量（1、2、3、4、5、6、7、8 m）的水流流速，并取平均流速作為不同水力工況條件下的水流流速（表1）[29]。另外，沿程測定含沙水樣濃度：分別從距離細溝出口的1、2、4、8 m處用4個300 mL容積的鋼杯收集泥沙水流樣品，采樣時間為30～60 s。每個設計工況條件下，水流流速測量與沿程水流含沙量沖刷試驗均各重復3次。之后將樣品靜置24 h后濾掉上層清液，放入105 ℃烘箱中烘干48 h，稱質量記錄并計算水流含沙量，并通過數值法、修正數值法和解析法分別計算得到細溝剝蝕率。

表1 不同水力工況條件下飽和黃綿土坡面沿程水流流速[29]

1.3 計算原理

在WEPP模型中細溝剝蝕率可用式（1）表示：

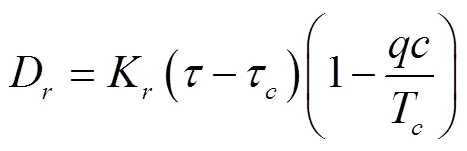
式中D是細溝剝蝕率，kg/(m2·s)；K是土壤可蝕性參數，s/m；是水流剪切應力，N/m2；τ是臨界剪切應力，N/m2；為單寬流量，m3/(s·m)；為水流含沙量，kg/m3；T為水流輸沙能力，kg/m3。在飽和土壤坡面上，清水中的含沙量為0，即水流剛剛進入細溝溝頭時細溝剝蝕率可視為最大值，因此由式（1）可得飽和土壤坡面最大細溝剝蝕率為

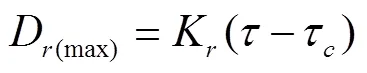
式中D(max)為飽和土壤坡面的最大細溝剝蝕率，kg/(m2·s)。由式（2）可知，確定不同設計試驗工況下最大細溝剝蝕率與水流剪切應力，就可通過擬合分析得到細溝可蝕性參數與臨界剪切應力。

1.3.1 數值法

根據細溝剝蝕率定義，細溝剝蝕率是細溝溝長的函數，且不隨時間變化[30]。基于質量守恒定律，在細溝剝蝕階段水流輸沙量的增量應與土壤剝蝕量相等，則對應的飽和土壤坡面細溝剝蝕率可用數值法近似計算獲得[31]，即：

式中為細溝溝長，m；為水流流量，m3/s；，為細溝溝寬，m；Δ為細溝溝寬增量，m；為單寬流量，m3/(s·m)，D1為數值法計算的細溝剝蝕率，kg/(m2·s)。已有研究表明[31]，飽和土壤坡面上細溝剝蝕率數值計算結果與水流含沙量有良好的線性函數關系，如式（4）：

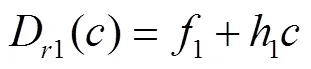
式中1為常數，kg/(m2?s)；1為比例系數，一般為負值，表示隨水流含沙量增加細溝剝蝕率下降的速率，m/s。從式（4）中可看出在飽和土壤坡面上水流的細溝剝蝕率隨水流含沙量的增大而呈線性減小。當水流含沙量為0時，細溝剝蝕率可達到其最大值。

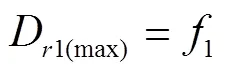
式中D1(max)為數值法計算的飽和土壤坡面最大細溝剝蝕率，kg/(m2·s)。

1.3.2 修正數值法

根據Huang等[32]獲得飽和土壤坡面細溝侵蝕過程中水流含沙量與細溝溝長的變化關系。

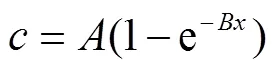
式中為水流達到輸沙能力時的最大水流含沙量，kg/m3；為隨細溝溝長增速的衰減系數，m-1。

由于數值法為近似計算，因此數值法計算獲得的細溝剝蝕率與真實值存在較大誤差。式（6）為單調增函數，且根據1.3.1節所述細溝剝蝕率數值計算原理，基于數學理論，總能在（x-1, x）區間上找到一點(ξ)使得式（7）成立。

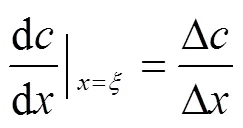
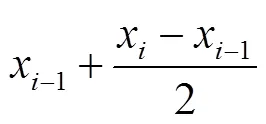
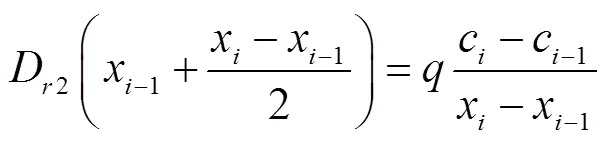
式中D2為修正數值法計算的飽和土壤坡面細溝剝蝕率，kg/(m2?s)；c-1和c分別表示細溝溝段內第-1和處水流含沙量，kg/m3。修正數值法可提高沿程細溝剝蝕率的計算精度，為后續的細溝侵蝕參數估算及模型構建提供基礎。采用修正數值法計算細溝剝蝕率與水流含沙量間的關系，如式（9）所示：

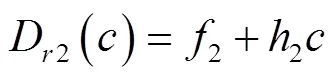
式中2為常數，kg/(m2?s)；2為式（9）中的比例系數，表示隨水流含沙量增加細溝剝蝕率下降的速率，m/s。從式（9）可看出，當水流含沙量為0時細溝剝蝕率可達到其最大值，如式（10）：

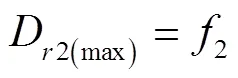
式中D2(max)為修正數值法計算的飽和土壤坡面最大細溝剝蝕率，kg/(m2?s)。

1.3.3 解析法

如式（3）所示，根據細溝剝蝕率的定義，當?趨近于0時，?/2也趨近于0。因此，根據極限的基本原理對式（3）進行轉換：

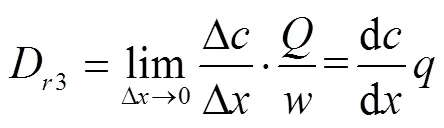
式中D3為解析法計算的飽和土壤坡面細溝剝蝕率(kg/(m2?s))，即依據數學原理精確計算所得的理論細溝剝蝕率。式（11）定義了解析法計算飽和土壤坡面細溝剝蝕率，因此將式（6）代入式（11）中可獲得通過細溝溝長解析計算細溝剝蝕率的式子，如下：

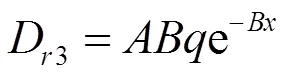
式中D3為通過細溝溝長解析計算的飽和土壤坡面細溝剝蝕率，kg/(m2?s)；是飽和土壤坡面測量最大水流含沙量，kg/m3；為相關系數m-1，表明細溝剝蝕率隨細溝溝長增加而降低的速率。采用解析法計算細溝剝蝕率與水流含沙量間的關系，如式（13）所示：

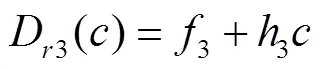
式中3為常數，kg/(m2?s)；3為式（13）中的比例系數，表示隨水流含沙量增加細溝剝蝕率下降的速率，m/s。由式（13）可知，當水流含沙量為0時，細溝剝蝕率可達到其最大值，如式（14）：

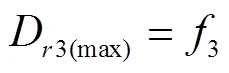
式中D3(max)為解析法計算的飽和土壤坡面最大細溝剝蝕率，kg/(m2?s)。

將式（2）分別代入式（5）、式（10）與式（14），可計算得到基于3種計算方法的飽和土壤坡面細溝侵蝕土壤可蝕性參數K和土壤臨界剪切應力τ：

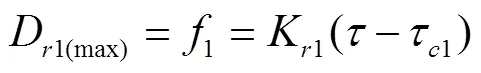
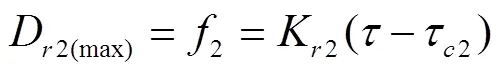
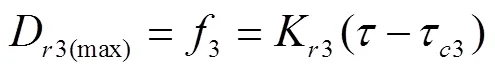
式中K1是基于數值法擬合的土壤可蝕性參數，s/m；τ1是基于數值法擬合的臨界剪切應力，N/m2；K2是基于修正數值法擬合的土壤可蝕性參數，s/m；τ2是基于修正數值法擬合的臨界剪切應力，N/m2；K3是基于解析法擬合的土壤可蝕性參數，s/m；τ3是基于解析法擬合的臨界剪切應力，N/m2。水流剪切應力（τ）為

式中是水的重力密度，9 800 N/m3；為地表坡度的正弦值；avg是侵蝕細溝的水流流速，m/s。

2 結果與分析

2.1 基于3種方法的土壤可蝕性參數與臨界剪切應力

基于WEPP模型原理，最大細溝剝蝕率是計算土壤可蝕性參數與臨界剪切應力的基礎。通過式（5）、式（10）和式（14）得出不同水力工況條件下數值法、修正數值法和解析法計算的最大細溝剝蝕率，如表2所示，3種方法所得結果在坡度為5和10°，流量為2 L/min時都較小，但在坡度為15°和20°，流量為4和8 L/min時逐漸增大。隨坡度增加，數值法計算的最大細溝剝蝕率明顯高于修正數值法和解析法，即數值法計算的最大細溝剝蝕率對于坡度更加敏感。例如流量為8 L/min時，坡度從10°變化至15°，數值法計算的最大細溝剝蝕率變化率為288.1%，而修正數值法與解析法計算的最大細溝剝蝕率變化率僅為156.0%和151.5%。而在同一坡度下，流量增加對3種方法計算的最大細溝剝蝕率的影響無明顯差異。整體來看，修正數值法和解析法計算的最大細溝剝蝕率更接近。

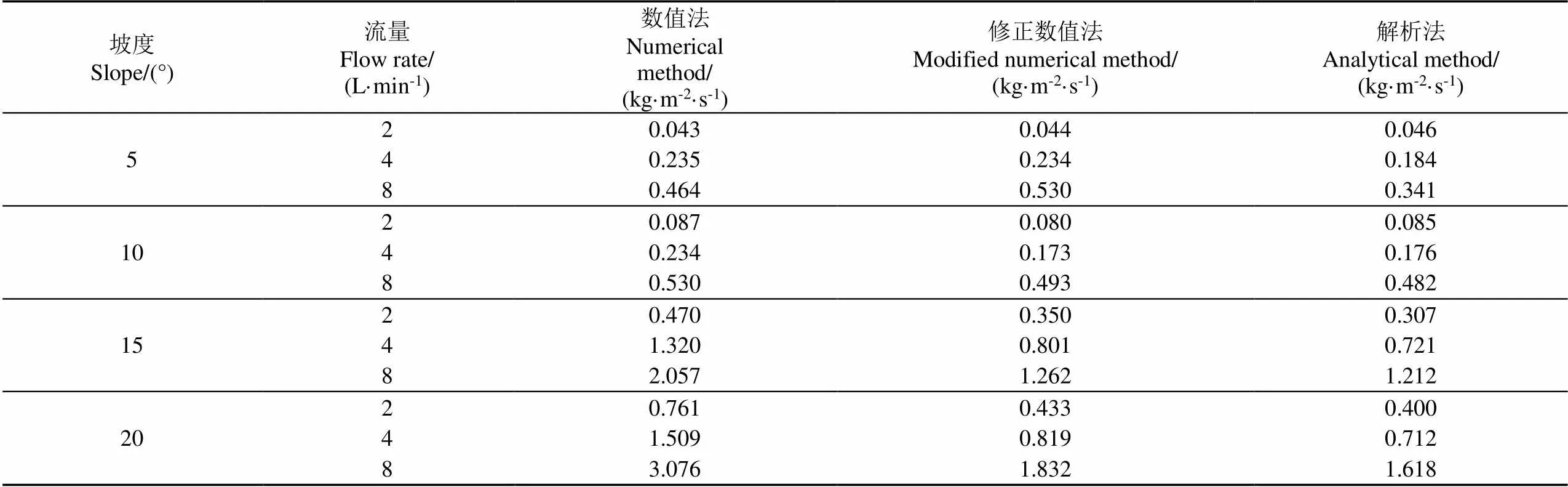
表2 數值法、修正數值法和解析法計算的最大細溝剝蝕率

根據最大細溝剝蝕率結果，運用式（18）計算獲得不同水力工況條件下的水流剪切應力，并根據式（15）、（16）和（17）分別進行線性回歸，所得結果如圖2所示。圖2a中直線的斜率即為基于數值法的土壤可蝕性參數0.470 s/m，圖2b中直線的斜率即為基于修正數值法的土壤可蝕性參數0.278 s/m，圖2c中直線的斜率即為基于解析法的土壤可蝕性參數0.256 s/m。當最大細溝剝蝕率為0時，此時水流剪切力即為臨界剪切應力，因此基于數值法計算的臨界剪切應力為1.502 N/m2，基于修正數值法的臨界剪切應力為1.306 N/m2，基于解析法的臨界剪切應力為1.367 N/m2。

將3種方法計算的飽和黃綿土坡面設計水力工況條件下土壤可蝕性參數及臨界剪切應力的結果進行對比，發現修正數值法與解析法計算的土壤可蝕性參數（0.278、0.256 s/m）和臨界剪切應力（1.306、1.367 N/m2）較為接近，數值法計算的土壤可蝕性參數較大（0.470 s/m、1.502 N/m2）。可見修正數值法較大程度提高了由實測數據近似計算細溝剝蝕率的準確性，使其與解析法計算獲得的理論細溝剝蝕率更為接近，從而提高了基于最大細溝剝蝕率計算所得土壤可蝕性參數和臨界剪切應力的精度。

圖2 基于數值法、修正數值法和解析法計算不同水力工況條件下最大剝蝕率與水流剪切應力的關系

2.2 飽和與未飽和黃綿土坡面細溝侵蝕的土壤可蝕性參數與臨界剪切應力對比

本課題組在前期研究中相同試驗條件獲得了基于解析法計算的未飽和黃綿土坡面土壤可蝕性參數與臨界剪切應力[4]。將之與本研究中基于修正數值法和解析法計算的飽和黃綿土坡面細溝侵蝕土壤可蝕性參數及臨界剪切應力進行對比，如表3所示。

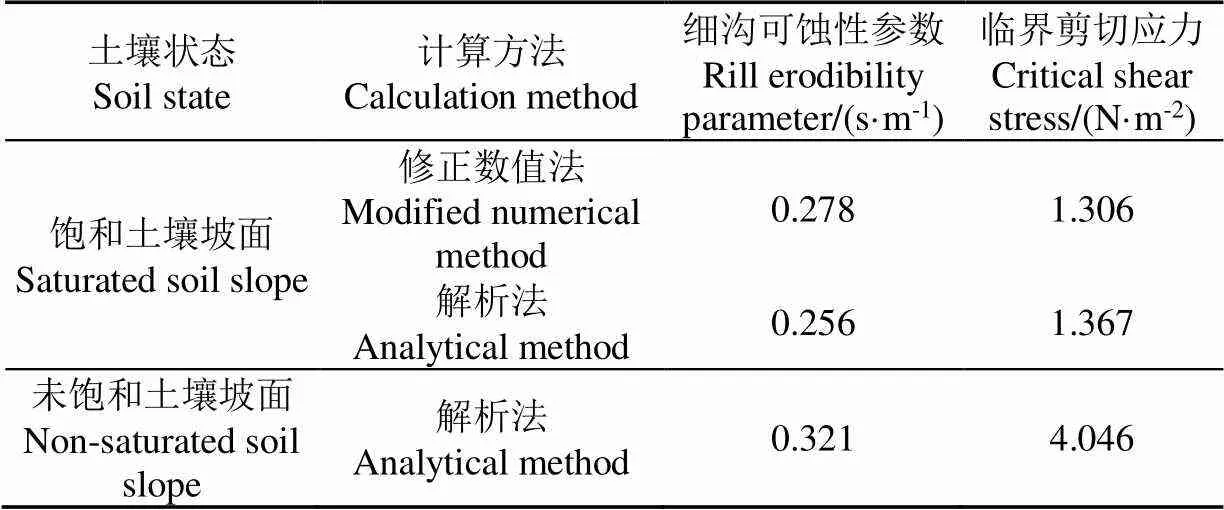
表3 飽和與未飽和黃綿土坡面土壤可蝕性參數與土壤臨界剪切應力

如表3所示，飽和黃綿土坡面修正數值法與解析法計算所得土壤可蝕性參數分別較未飽和黃綿土坡面解析法計算土壤可蝕性參數結果小13.40%和20.25%，平均上小16.83%，但飽和黃綿土坡面修正數值法與解析法計算的臨界剪切應力分別較未飽和黃綿土坡面解析法計算的臨界剪切應力小67.72%和66.21%，平均小66.97%。說明盡管飽和黃綿土坡面細溝侵蝕過程中泥沙輸送能力和細溝水流含沙濃度比未飽和黃綿土坡面大[22,32]，但對于給定類型的土壤，土壤可蝕性參數是一個較為穩定的值[14,34]，土壤飽和對土壤可蝕性參數的影響小，但對臨界剪切應力影響大。一方面，土壤飽和導致土壤顆粒之間黏結力減弱，土壤團聚體易分解為單顆粒，使得土壤強度顯著降低，致使土壤抵抗徑流剪切的能力降低[29,35]；另一方面，土壤飽和使得土壤顆粒間隙在孔隙水壓力影響下增大，且顆粒間的摩擦顯著減小，從而導致土壤的臨界剪切應力降低[16]。因此，飽和與未飽和狀態下的黃綿土臨界剪切應力相差較大，也是飽和黃綿土坡面細溝侵蝕輸沙量更大的原因。上述結果表明，土壤飽和主要導致了黃綿土抵抗徑流剪切破壞的能力大幅度降低，從而使得黃綿土坡面飽和后更易發生細溝侵蝕。

2.3 飽和黃綿土與紫色土坡面細溝侵蝕的土壤可蝕性參數與臨界剪切應力對比

前期研究[2]基于修正數值法和解析法計算得到飽和紫色土坡面細溝剝蝕率，之后通過最大細溝剝蝕率與水流剪切應力回歸分析，獲得飽和紫色土坡面在相同坡度與流量條件下的土壤可蝕性參數和臨界剪切應力。與本文研究結果對比（表4），分析得出飽和狀態下黃綿土坡面解析法與修正數值法計算所得土壤臨界剪切應力分別比紫色土坡面大4.68%和小2.10%，整體差異不大。但飽和黃綿土坡面解析法與修正數值法計算所得土壤可蝕性參數分別比紫色土坡面大2.16倍和2.35倍，平均大2.26倍。原因可能是黃綿土粉粒含量高、有機質含量低，而紫色土黏粒含量高、有機質含量高，且有研究表明黏粒和有機質含量越高，土壤可蝕性參數越小[14,36]。此外，黃綿土黏聚力低，黏結性差，土壤剖面結構不良，使得黃綿土容易侵蝕；而紫色土通常是豐富的不完全風化粗土塊，不易被侵蝕。因此，2種土壤在飽和狀態下，黃綿土較紫色土更易分散為小顆粒，易發生侵蝕[37]，黃綿土的土壤可蝕性參數顯著高于紫色土。黃綿土與紫色土在飽和狀態下的臨界剪切應力相近，但土壤可蝕性參數相差較大，說明土壤類型更大程度上決定了土壤可蝕性參數，因此土壤飽和對其他土壤類型的土壤可蝕性參數和臨界剪切應力影響值得進一步探究。

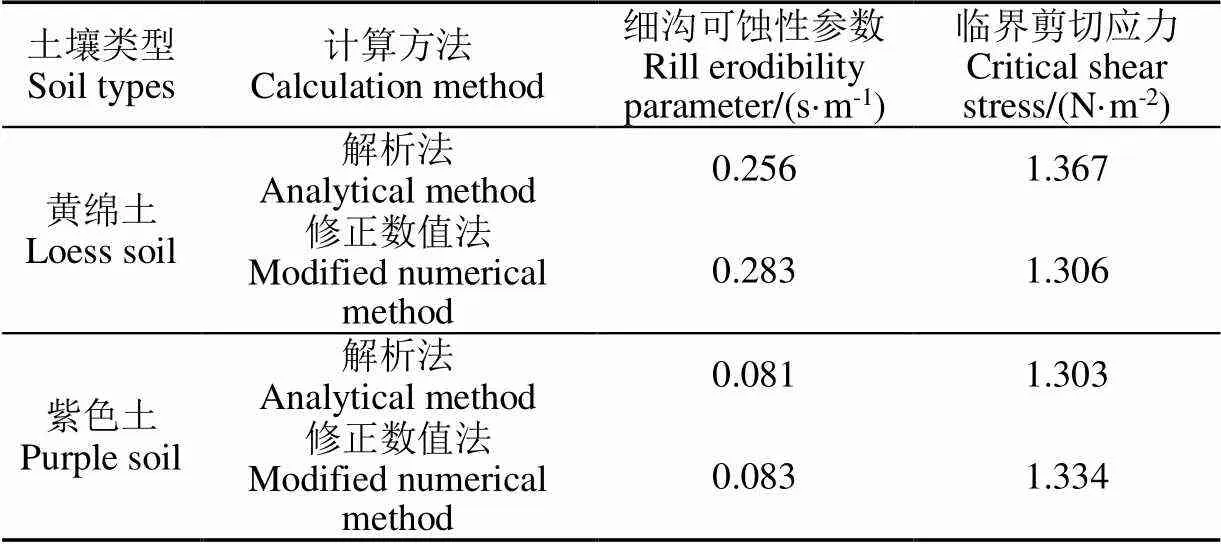
表4 飽和狀態下黃綿土與紫色土的土壤可蝕性參數與臨界剪切應力

3 結 論

本文基于飽和黃綿土坡面細溝侵蝕水流流速與沿程含沙量試驗，采用數值法、修正數值法和解析法計算不同水力工況條件下細溝剝蝕率，獲得最大細溝剝蝕率，而后通過最大細溝剝蝕率與水流剪切應力的線性回歸獲得飽和黃綿土坡面細溝侵蝕的土壤可蝕性參數和臨界剪切應力，結果表明：1）3種方法所得土壤可蝕性參數分別是0.470、0.278和0.256 s/m，臨界剪切應力分別為1.502、1.306和1.367 N/m2。修正數值法可提高數值法近似計算的精度，使近似計算結果更接近解析法計算獲得的理論值。2）飽和狀態下黃綿土坡面細溝侵蝕的土壤可蝕性參數較與未飽和土壤平均減小16.83%，臨界剪切應力相較于未飽和黃綿土坡面平均減小66.97%；說明同一土壤類型的坡面在飽和前后土壤可蝕性參數相近，但臨界剪切應力變化較大，土壤飽和極大影響了臨界剪切應力，從而使得黃綿土坡面飽和時更易發生細溝侵蝕。3）對不同飽和土壤而言，飽和狀態下黃綿土坡面的臨界剪切應力與紫色土差異不大，而土壤可蝕性參數比紫色土大2.26倍，說明2種土壤在飽和狀態下的臨界剪切應力相近，但土壤可蝕性參數相差較大，即土壤類型對土壤可蝕性參數起決定性作用。土壤飽和使得臨界剪切應力降低導致土壤坡面細溝侵蝕加劇，且不同土壤類型坡面的土壤可蝕性參數與臨界剪切應力受飽和狀態的影響不同，因此進一步探究土壤飽和對不同土壤類型土壤坡面的影響可為完善土壤侵蝕預報物理模型提供科學依據。

[1] Chen X Y, Zhao Y, Mi H X, et al. Estimating rill erosion process from eroded morphology in flume experiments by volume replacement method[J]. Catena, 2016, 136: 135-140.

[2] Li D D, Chen X Y, Han Z, et al. Determination of rill erodibility and critical shear stress of saturated purple soil slopes[J]. International Soil and Water Conservation Research, 2021, 10(1): 38-45.

[3] 趙宇輝，張建軍，于洋，等. 晉西黃土區蔡家川小流域切溝的空間分布及形態特征[J]. 農業工程學報，2022，38(4)：151-158.

Zhao Yuhui, Zhang Jianjun, Yu Yang, et al. Spatial distribution and characteristics of the gullies in Caijiachuan watershed in loess region of Western Shanxi Province, China[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(4): 151-158. (in Chinese with English abstract)

[4] Lei T W, Zhang Q W, Yan L J, et al. A rational method for estimating erodibility and critical shear stress of an eroding rill[J]. Geoderma, 2008, (3/4): 628-633.

[5] 陳平安，雷孝章. 美國土壤侵蝕模型研究綜述[C]//劉國東，梁川，覃光華. 河流開發、保護與水資源可持續利用—第六屆中國水水壇水論壇論文集. 北京：中國水利水電出版社，2008：1018-1023.

Chen Pingan, Lei Xiaozhang. A review of soil erosion models in the United States[C]//Liu Guodong, Liang Chuan, Qin Guanghua. River Development and Protection and Sustainable Utilization of Water Resources—The Sixth China Water Forum Proceedings. Beijing: China Water&Power Press, 2008: 1018-1023. (in Chinese with English abstract)

[6] 周正朝，上官周平. 土壤侵蝕模型研究綜述[J]. 中國水土保持科學，2004，2(1)：52-56.

Zhou Zhengchao, Shangguan Zhouping. Overview on soil erosion model research[J]. Science of Soil and Water Conservation in China, 2004, 2(1): 52-56. (in Chinese with English abstract)

[7] 張晴雯，雷廷武，潘英華，等. 細溝侵蝕可蝕性參數及土壤臨界抗剪應力的有理（實驗）求解方法[J]. 中國科學院研究生院學報，2004，21(4)：468-475.

Zhang Qingwen, Lei Tingwu, Pan Yinghua, et al. Rational computational method of soil erodibility and critical shear stress from experimental data[J]. Journal of Graduate School of Chinese Academy of Sciences, 2004, 21(4): 468-475. (in Chinese with English abstract)

[8] van Klaveren R W, McCool D K. Erodibility and critical shear of a previously frozen soil[J]. Transactions of the ASAE, 1998, 41(5): 1315-1321.

[9] 劉寶元，張科利，焦菊英. 土壤可蝕性及其在侵蝕預報中的應用[J]. 自然資源學報，1999，14(4)：345-350.

Liu Baoyuan, Zhang Keli, Jiao Juying. Soil erodibility and its use in soil erosion prediction model[J]. Journal of Natural Resources, 1999, 14(4): 345-350. (in Chinese with English abstract)

[10] Hanson G J, Hunt S L. Lessons learned using laboratory JET method to measure soil erodibility of compacted soils[J]. Applied Engineering in Agriculture, 2007, 23: 305-312.

[11] Singh H V, Thompson A M. Effect of antecedent soil moisture content on soil critical shear stress in agricultural watersheds[J]. Geoderma, 2016, 262: 165-173.

[12] 邢行，陳曉燕，韓珍，等. 飽和與非飽和黃綿土細溝徑流水動力學特征及侵蝕阻力對比[J]. 水土保持學報，2018，32(3)：92-97.

Xing Hang, Chen Xiaoyan, Han Zhen, et al. Comparation of hydrodynamic characteristics and flow resistance under rill erosion between saturated and unsaturated loess soil[J]. Journal of Soil and Water Conservation, 2018, 32(3): 92-97. (in Chinese with English abstract)

[13] Nouwakpo S K, Huang C H, Bowling L, et al. Impact of vertical hydraulic gradient on rill erodibility and critical shear stress[J]. Soil Science Society of America Journal2010, 74(6): 1914-1921.

[14] 王彬，鄭粉莉，王玉璽，等. 東北典型薄層黑土區土壤可蝕性模型適用性分析[J]. 農業工程學報，2012，28(6)：126-131.

Wang Bin, Zheng Fenli, Wang Yuxi, et al. Adaptability analysis on soil erodibility models in typical thin layer black soil area of Northeast China[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(6): 126-131. (in Chinese with English abstract)

[15] Su Z G, Xiong D H, Zhang J H, et al. Variation in the vertical zonality of erodibility and critical shear stress of rill erosion in China’s Hengduan Mountains[J]. Earth Surface Processes and Landforms, 2019, 44(1): 88-97.

[16] Han Z, Chen X Y, Li Y H, et al. Quantifying the rill-detachment process along a saturated soil slope[J]. Soil and Tillage Research, 2020, 204: 104726.

[17] Liu Q J, Wells R R, Dabney S M, et al. Effect of water potential and void ratio on erodibility for agricultural soils[J]. Soil Science Society of America Journal, 2017, 81(3): 622-632.

[18] Bullock M S, Nelson S D, Kemper W D. Soil cohesion as affected by freezing, water content, time and tillage[J]. Soil Science Society of America Journal, 1988, 52(3): 770-776

[19] 董月群，李淑芹，原翠萍，等. 黑麥草對黃土坡面降雨產流產沙過程的影響[J]. 中國農業大學學報，2011，16(4)：67-73.

Dong Yuequn, Li Shuqin, Yuan Cuiping, et al. Impacts of rye grasses on runoff and sedimentation processes from loess slopes[J]. Journal of China Agricultural University, 2011, 16(4): 67-73. (in Chinese with English abstract)

[20] 安娟，鄭粉莉，李桂芳，等. 不同近地表土壤水文條件下雨滴打擊對黑土坡面養分流失的影響[J]. 生態學報，2011，31(24)：7579-7590.

An Juan, Zheng Fenli, Li Guifang, et al. Effect of raindrop impact on nutrient losses under different near-surface soil hydraulic conditions on black soil slope[J]. Acta Pedologica Sinica, 2011, 31(24): 7579-7590. (in Chinese with English abstract)

[21] Wu B, Wang Z L, Zhang Q W, et al. Evaluation of shear stress and unit stream power to determine the sediment transport capacity of loess materials on different slopes[J]. Journal of Soils and Sediments, 2018, 18: 116-127.

[22] Huang Y H, Li F H, Liu Z Q, et al. Experimental determination of sediment transport capacity of concentrated water flow over saturated soil slope[J]. European Journal of Soil Science, 2020, 72(2): 756-768.

[23] 孫樹林，王利豐. 飽和、非飽和有機質粉土抗剪強度的對比[J]. 巖土工程學報，2006，28(11)：1932-1935.

Sun Shulin, Wang Lifeng. Comparison of shear strength between saturated and unsaturated sandy silt[J]. Journal of Geotechnical Engineering, 2006, 28(11): 1932-1935. (in Chinese with English abstract)

[24] 滕延京，盛志強，王曙光. 飽和黏性土抗剪強度的試驗方法[J]. 巖土工程學報，2015，37(3)：426-431.

Teng Yanjing, Sheng Zhiqiang, Wang Shuguang. Test method for shear strength of saturated cohesive soil[J]. Journal of Geotechnical Engineering, 2015, 37(3): 426-431. (in Chinese with English abstract)

[25] Saffari P, Noor M J M, Ashaari Y, et al. Shear strength of unsaturated malaysian granitic residual soil[J]. Journal of Testing and Evaluation, 2019, 47(1): 640-653.

[26] 王偉，陳楊，莊曉暉，等. 極端降雨條件下秸稈覆蓋坡面水流流速空間分布[J]. 農業工程學報，2022，38(2)：149-156.

Wang Wei, Chen Yang, Zhuang Xiaohui, et al. Spatial distribution of overland flow velocity along straw-mulched slope under extreme rainfall[J]. Journal of Geotechnical Engineering (Transactions of the CSAE),2022, 38(2): 149-156. (in Chinese with English abstract)

[27] 沈海鷗, 鄭粉莉, 溫磊磊. 細溝發育與形態特征研究進展[J].生態學報，2018，38(19)：6818-6825.

Shen Haiou, Zheng Fenli, Wen Leilei. A research review of rill development and morphological characteristics[J]. Acta ecologica sinica, 2018, 38(19): 6818-6825. (in Chinese with English abstract)

[28] 張科利, 秋吉康宏. 坡面細溝侵蝕發生的臨界水力條件研究[J]. 土壤侵蝕與水土保持學報，1998(1)：42-47.

Zhang Keli, Qiuji Kanghong. Critical hydraulic condition of rill erosion onsloping surface[J]. Journal of Soil Erosion and Soil and Water Conservation, 1998(1): 42-47. (in Chinese with English abstract)

[29] Huang Y H, Chen X Y, Li F H, et al. Velocity of water flow along saturated loess slopes under erosion effects[J]. Journal of Hydrology, 2018, 561: 304-311.

[30] Lei T W, Zhang Q W, Zhao J, et al. A laboratory study of sediment transport capacity in the dynamic process of rill erosion[J]. Transactions of the ASAE, 2001, 44(6): 1537-1542.

[31] Lei T W, Zhang Q W, Zhao J, et al. Soil detachment rates for sediment loaded flow in rills[J]. Transactions of the ASAE, 2002, 45(6): 1897-1903.

[32] Huang Y H, Wang W, Lei T W, et al. Saturation effect on the distribution of rill detachment rate[J]. European Journal of Soil Science, 2021, 72(5): 2076-2087.

[33] 黃鈺涵. 飽和土壤坡面細溝侵蝕動力機制試驗研究[D]. 北京：中國農業大學，2020.

Huang Y H. Experimental Study on the Dynamic Mechanism of Rill Erosion over Saturated Soil Slope[D]. Beijing: China Agricultural University, 2020. (in Chinese with English abstract)

[34] Huang C H, Bradford J M, Laflen J M. Evaluation of the detachmenttransport coupling concept in the wepp rill erosion equation[J]. Soil Science Society of America Journal, 1996, 60(3): 734-739.

[35] Chen X Y, Huang Y H, Zhao Y, et al. Comparison of loess and purple rill erosions measured with volume replacement method[J]. Journal of Hydrology, 2015, 530: 476-483.

[36] 劉紀根，張平倉，陳展鵬. 聚丙烯酰胺對擾動紅壤可蝕性及臨界剪切力的影響[J]. 農業工程學報，2010，26(7)：45-49.

Liu Jigen, Zhang Pingcang, Chen Zhanpeng. Effects of Polyacrylamide (PAM) on soil erodibility and critical shear stresses for disturbed red soil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(7): 45-49. (in Chinese with English abstract)

[37] Xing H, Huang Y H, Chen X Y, et al. Comparative study of soil erodibility and critical shear stress between loess and purple soils[J]. Journal of Hydrology, 2018, 558: 625-631.

Characteristics of soil erodibility parameter and critical shear stress on saturated loess soil slope

Huang Yuhan1,2, Yang Mengge2, Lei Tingwu1※, Li Fahu1, Wang Wei3

(1.,,100083,;2.,,,530004,;3.,100083,)

Soil erodibility parameter and critical shear stress are important indicators to evaluate the degree of soil erosion sensitivity and the resistance to the shear deformation of water flow. To date, the change of soil erodibility parameter and critical shear stress is unclear in the rill erosion process of saturated loess soil slope. In this study, the maximum rill detachment rates of saturated loess soil slope were determined by a series of soil scouring experiments in the laboratory under different slopes (5°, 10°, 15°, and 20°) and flow rates (2, 4, and 8 L/min). Then, the numerical, modified numerical, and analytical approaches were utilized to calculate the soil erodibility parameters and critical shear stresses. The results showed that the maximum rill detachment rates calculated by the three methods increased with the increase of slope and flow rate over saturated loess soil slope, and the maximum rill detachment rates calculated by the modified numerical method were similar with those calculated by the analytical method. The soil erodibility parameters were 0.470, 0.278, and 0.256 s/m, respectively, and the critical shear stresses were 1.502, 1.306, and 1.367 N/m2, respectively. The modified numerical method improved the calculation accuracy, thus the modified numerical calculation was close to the theoretical value calculated by the analytical method. The soil erodibility parameters of saturated loess soil slope decreased by 16.83%, and the critical shear stresses decreased by 66.97%, compared with those of non-saturated loess soil slope in the same study area. Soil saturation had no significant effect on the soil erodibility parameters, while greatly reducing soil critical shear stress, and then leading to serious soil erosion on loess soil slope. Besides, the critical shear stresses of the saturated loess soil slope were 6.38% larger than those of the saturated purple soil slope, and the soil erodibility parameters of the saturated loess soil slope were 2.26 times those of the saturated purple soil slope. These results indicated that the soil saturation had similar effects on the critical shear stress of the two soils, while the saturated loess soil was more sensitivity on soil erosion than the saturated purple soil. These findings can provide some references to optimize the rill erosion model parameters in different soil slopes under the condition of saturations.

soils; erosion; rills; erodibility parameter; critical shear stress; saturation; maximum rill detachment rate

10.11975/j.issn.1002-6819.2022.17.009

S224.2

A

1002-6819(2022)-17-0083-08

黃鈺涵，楊夢格，雷廷武，等. 飽和狀態下黃綿土坡面細溝侵蝕可蝕性和臨界剪切應力特征[J]. 農業工程學報，2022，38(17)：83-90.doi：10.11975/j.issn.1002-6819.2022.17.009 http://www.tcsae.org

Huang Yuhan, Yang Mengge, Lei Tingwu, et al. Characteristics of soil erodibility parameter and critical shear stress on saturated loess soil slope[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(17): 83-90. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.17.009 http://www.tcsae.org

2022-05-18

2022-07-10

國家自然科學基金面上項目（41571257）

黃鈺涵，博士，講師，研究方向為土壤侵蝕機理、土壤水文與水土保持。Email：huangyuhan0710@foxmail.com

雷廷武，博士，教授，博士生導師，研究方向為土壤侵蝕機理、土壤水文與水土保持。Email：leitingwu@cau.edu.cn