核設施退役數字仿真中人員行走最優路徑研究

古 強，寇驕子，李文濤

（中核四川環保工程有限責任公司，四川 廣元 628017）

全球已有140 多座核電反應堆永久關閉，開始或等待退役。在運行的反應堆中，有部分也已超出設計壽期。除核電反應堆外，一些國家還有大量的遺留軍用核設施需要退役，這些工作均面臨不同程度的難題和挑戰，尤其是在退役策略選擇、輻射安全和成本預算方面存在很大的不確定性，需要大量的準備工作，以達到方案最優化。

消除這種不確定性的有效方法之一是利用仿真技術。利用仿真技術可為退役策略和方案的選定、操作順序的優化、退役廢物數量的估算和形狀的判斷、輻射劑量的估計以及退役操作前人員的培訓等多項工作提供有效的支持，使整個退役過程從放射性廢物產生到成本盡量低等多個方面真正符合合理可行原則。

近年來，我國對于核設施退役監管要求越來越嚴。同時，加大了核設施退役投入，并在部分退役技術方面取得了一定的突破。但在具體的退役實踐經驗還較為欠缺，對于在退役活動中操作人員的安全和健康的保障具體措施的研究應用還較少。因此，本課題是對核設施數字化仿真中人員行走的最優路徑進行研究，基于推導計算出的輻射場分布，按照在相同工作時間，人體受照劑量的累計值最低，采用A-Star 算法進行兩點間最優路徑的計算，將最優路徑轉換為數字化仿真模型中的尋路模型進行呈現，這是在核設施數字化仿真退役中一次重要的嘗試，將為核設施真實退役提供重要參考。

1 基本理論模型

圖論研究中的一個經典算法是最短路徑算法，即在圖中找到2 個結點之間最短的路徑。

計算最短路徑的算法即“最短路徑算法”。常用最短路徑算法包括：迪杰斯特拉算法，即Dijkstra 算法；SPFA 算法Bellman-Ford 算法，即隊列優化算法；弗洛伊德算法（Floyd）Floyd-Warshall 算法；Johnson 算法；A-Star 算法。

本項目主要采用A-Star 算法進行研究。該算法是基于啟發式搜索，即在狀態空間中對每個搜索的位置進行評估，以確定最好的位置，再從這個位置搜索直至到達目標。這樣省略了搜索大量沒有作用的路徑，使得效率得到了提升。在啟發式搜索中，位置的估價是極其重要的方面，不同的估價可能到達不同的效果，其缺點是在長路徑上的速度呈現幾何級數地提升。

2 項目數據源

本項研究以待退役核設施為原型，采用3dMax、Unity 等三維仿真工具和平臺，對待退役核設施的主要建筑、設備、管線等進行了三維模型構建。同時，利用蒙特卡洛程序對輻射場進行計算，基于有限的輻射場數據，采用神經網絡插值的方法重構了輻射場。采用虛擬現實技術的核輻射可視化方法，將輻射場與設施疊加，用以分析和處理輻射信息，解決實時對輻射場進行渲染呈現的問題，并以多種圖形化的方式直觀地顯示核輻射劑量場的分布情況。

采用柵格路徑對設施內部空間進行了分隔。柵格路徑是搜索算法基于柵格地圖得到的一個柵格序列（數組），是本項目研究在路徑算法的實踐之一。柵格法的使用與障礙物柵格的生成，進而將實際三維仿真地圖轉換為柵格地圖，柵格路徑無法直接應用于實際地圖中，需要將其進行處理，將柵格路徑轉換為直角坐標系下的路徑。在項目研究中，將核設施內部的空間按照標準的大小進行柵格繪制，形成了地理柵格內部空間結構，用于與輻射場進行耦合計算，采用A-Star 算法進行路徑尋址，最終找到最優路徑。

3 A-Star 啟發式搜索在輻射場尋址中的應用

3.1 A-Star 啟發式搜索研究

設從A 點移動到B 點，但是這兩點之間被一堵墻（不可走區域）隔開，首先把搜索區域簡化為了二維數組，數組的每一項代表一個格子柵格被定義成2 個狀態，即可走（walkable）和不可走（unwalkable）。通過計算出從A 到B 需要走過哪些節點，就找到了路徑。一旦路徑找到了，便可以從一個節點的中心移動到另一個節點的中心，直至到達目的地。

A-Star 算法核心公式就是F 值的計算

F=G+H，

式中：F 為總移動代價；G 為開始點到當前節點的移動代價；H 為當前節點到結束點的預估移動代價。

3.1.1 G 值的計算

假設當前A 節點，鄰近有8 個格子可走（上、下、左、右、右上、右下、左上、左下），當往上、下、左、右這4個格子走時，移動代價為10；當往左上、左下、右上、右下這4 個格子走時，移動代價為14。（等腰直角三角形勾股定理：斜邊2=2×直角邊2）。

基本公式為

G=移動代價。

根據環境應用的需要，G 值的計算可以進行拓展。如加上柵格不同輻射場量因素對尋路的影響，可以給不同柵格賦予不同代價因子，來體現出G 值的差異。由于輻射場估算已經給每一個柵格賦予了輻射場值，可以利用該數值轉換為代價因子，在移動代價相同情況下，低場量的G 值更低，算法就會傾向選擇G 值更小的低場量柵格。

拓展公式為

G=移動代價×代價因子。

3.1.2 H 值的計算

19世紀，赫爾曼·閔可夫斯基創造了曼哈頓距離（Manhattan Distance）一詞，其是一種幾何用語。在幾何度量空間里，用于標明在標準坐標系上2 個點的絕對軸距的總和，即兩點在南北方向上的距離加上在東西方向上的距離之和。

二維平面兩點a（x1，y1）與b（x2，y2）間的曼哈頓距離為

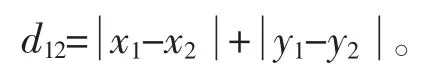
n 維空間點a（x11，x12，…x1n）與b（x21，x22…x2n）的曼哈頓距離為

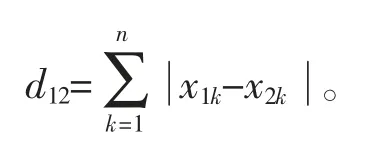
A-Star 算法之所以被認為是具有啟發策略的算法，在于其可通過預估H 值，降低走彎路的可能性，更容易找到一條更短的路徑。其他不具有啟發策略的算法，沒有做預估處理，只是窮舉出所有可通行路徑，然后從中挑選一條最短的路徑。這也是A-Star 算法效率更高的原因。

3.1.3 開始搜索

開放列表（open list）用于記錄所有可考慮選擇的格子。

封閉列表（close list）用于記錄所有不再考慮的格子。

（1）算法開始，首先搜索A 相鄰的所有可能的移動位置，每個節點左上角的值G 表示該點到A 的距離，這里的H 就取其到B 的曼哈頓距離。最后，還要計算一個F 值，F=H+G。

（2）此時的起點A，將其加入由節點組成的開放列表之中，開放列表即是一個待檢查的節點列表。

（3）查看與起點A 相鄰的節點，把其中可走的（walkable）或可到達的（reachable）節點也加入到開放列表（open list）中。隨后把A 從開放列表（open list）中移除，加入到封閉列表（close list）中，封閉列表（close list）中的每個節點都是現在不需要再關注的。

（4）從開放列表（open list）中選一個與起點A 相鄰的節點，選擇具有最小F 值的那個節點。

3.1.4 再次搜索

（1）接著把當前節點A1 從開放列表（open list）移到封閉列表（close list）中，搜索當前節點相鄰的所有可能的移動位置，并且都加入到開放列表（open list）。

（2）把找到最小F 值的節點A2 從開放列表（open list）移到封閉列表（close list）中，然后檢查與其相鄰的節點。其右邊的節點是墻壁（不可走unwalkable），進行忽略。左邊的節點是父節點，在封閉列表（close list）中，也進行忽略。其他相鄰的節點均在開放列表（open list）中，所以A2 節點尋路失敗，選擇開放列表（open list）中最小F 值的節點（列表中如果有多個最小F 值的情況，隨機獲取一個最小F 值節點進行下一次循環）。

（3）繼續把找到最小F 值的節點A3 從開放列表（open list）移到封閉列表（close list）中，然后檢查與其相鄰的節點。按照如此循環直到移動到目標點B。最終過程結果如圖1所示。

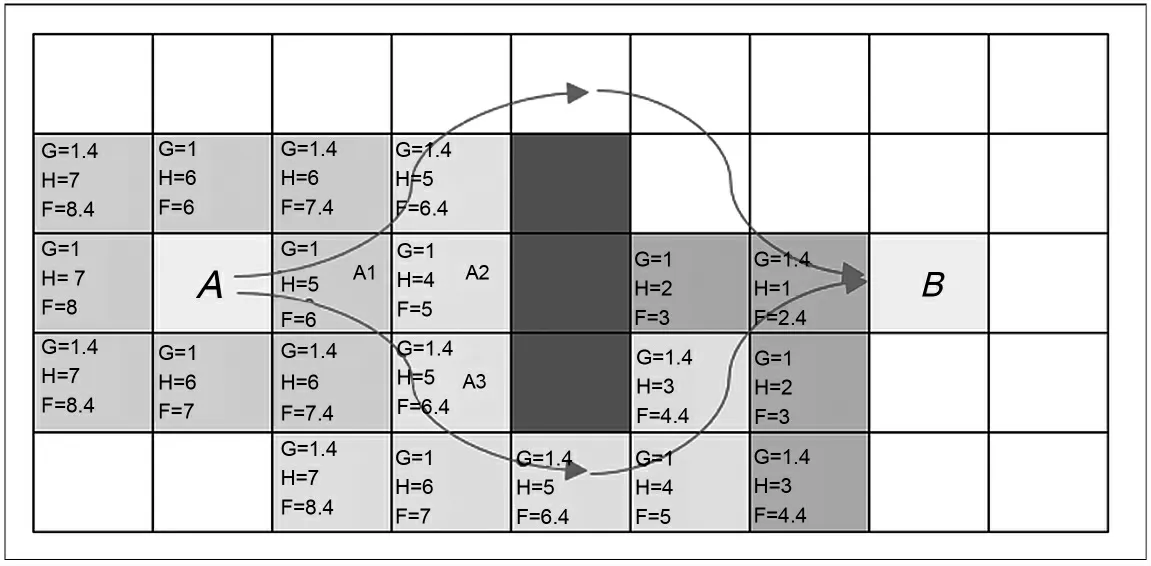
圖1 路徑搜索

3.1.5 補充

（1）最佳路線可能有多條，比如本文的示例，這取決于當開放列表（open list）存在多個F 值最小的節點時，先選取哪一個進行搜索。

（2）曼哈頓距離只是估算H 值最簡單的一種方法，常用的方法還有歐幾里德距離、切比雪夫距離等。

（3）實際應用中，為提高效率，還可以進行雙向搜索。從起點和終點分別發起搜索，一方搜索到另一方的已檢查節點時，即找到最佳路線。地圖較復雜時，雙向搜索可以顯著減少尋路過程中檢查的節點數量。

3.1.6 輻射場與代價因子

前文提到的“G=移動代價×代價因子”，如何將當前柵格輻射場量轉化為合理的代價因子是核退役數字化仿真中人員行走路徑最優化研究項目中的應用特殊性。

在理論上，通過源項調查獲取的輻射場數值范圍不常在一個數量級單位波動，需要使其數據標準化，將其限定在需要的一定的范圍之內。將數據進行標準化就是將數據按照一定的比例進行縮放，讓數據落入小范圍的特定區間內。采用比較和評價進行指標處理時會經常用到，讓數據不再受單位的限制，而將其轉化純數字，這種純數值是無量綱的，這樣對不同單位或量級的數據指標就能夠進行加權和比較。在分析數據之前，應將數據進行標準化，并分析標準化后的數據。數據標準化即將統計的數據指數化。數據無量綱處理和同趨化處理是數據標準化處理的兩個方面。數據無量綱化處理主要用于解決數據的可比性問題。數據同趨化處理主要解決不同性質的數據問題，即對不同性質指標加總不能正確反映不同作用力的綜合結果，首先應考慮改變逆指標數據的性質，使所有指標對測評方案的作用力同趨化，再加總以得到正確的結果。經過以上所述的標準化處理，將原始數據轉換為無量綱化指標測評值，這樣原始數據通過轉換已經處于同一數量級別，再進行綜合測評分析。

經常使用的方法包含如下幾種。

（1）簡單縮放。

（2）逐樣本均值消減（也稱為移除直流分量）。

（3）特征標準化（使數據集中所有特征都具有零均值和單位方差）。

其目的都是在于加快梯度下降求最優解的速度，有可能提高精度。

通常的方法：

（1）線性標準化，即min-max 標準化或離差標準化，就是對原始數據進行線性變換，最終結果值映射到[0，1]區間之間。采用以下函數進行轉換

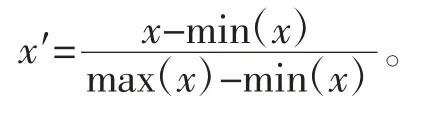
以上方法更適用于數值較為集中的情況。另外，這種方法也有明顯的缺陷，即一旦max 和min 不穩定，結果很可能也不穩定，這將直接影響使用效果。

（2）Z-score 標準化，或者稱為標準差歸一化，這種方法將原始數據的均值（mean，μ）和標準差（standard deviation，σ）進行數據標準化。數據處理后符合標準的正態分布，即均值為0，標準差為1，轉化函數為

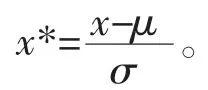
（3）非線性歸一化，一般應用于數據分析較大的場景，采用數學函數將原始值進行映射。這經常使用到log、指數、正切等函數，最終將根據數據分布的具體情況決定非線性函數的曲線。

3.2 在輻射場尋址中的應用

采用虛擬現實技術對核設施退役過程中三維輻射場進行計算和評估，給定核設施退役作業過程場景，以此為基礎構建目標問題動態三維輻射場模型，并對輻射劑量場采用蒙特卡洛數值模擬計算以及全范圍的可視化呈現，既在人員的安全性上有足夠的保障，又在經濟性和可靠性上具有顯著優勢。

基于構建的核設施退役環境中的三維輻射場，進行核設施退役作業過程的建模并完成路線規劃，如圖2所示。

圖2 輻射場中路線規劃實現

基于虛擬仿真平臺構建輻射場的三維仿真模型，將三維模型轉化為基本的幾何體，識別基本幾何體的基本信息，為快速計算輻射場，利用蒙特卡洛程序進行核輻射場計算。利用有限的輻射場數據，采用神經網絡插值的方法對輻射場進行重構，并采用虛擬現實技術實現核輻射可視化的方法，對輻射數據進行分析和處理，再將核設施與輻射場進行疊加，同時實現核輻射場實時渲染，進而以更直觀高效的圖形化方式呈現輻射劑量場的分布情況。

根據待退役核設施前期源項調查選取的4 000 個點位數據，選擇其中2 000 個點的數據作為輸入，在已知源項幾何大小、活度、產生射線的種類和射線能量等基礎信息上，利用蒙特卡洛程序及神經網絡插值進行三維輻射場劑量分布情況進行可視化建模與分析。通過建立的算法進行仿真模擬，并用其余2 000 個點的數據對仿真結果和實際數據進行相對誤差分析，不斷調整算法模型參數，直到模擬輻射場與實際數字誤差達到最小，最終確定輻射場模擬算法，實現了輻射場仿真分布誤差小于30%的指標。

使用柵格法將核設施結構和輻射場離散化，進而對人員行走路徑進行不斷優化。在處于二維環境下時，建立了基于柵格的路徑評估方法，用于評價路徑選擇的各種因素，并且基于圖論算法設計了受到最小輻照的路徑搜索方法，最終用于人員受照劑量最小的路徑的選擇。

在復雜的輻射環境下，采用組合優化的方法得到最小輻照路徑的最優解。本次開發的人員行走路徑優化方法和虛擬仿真技術相結合，不僅實現了核輻射場中人員行走路徑仿真，還能夠提供工作人員行走路徑規劃設計、優化、演練和評估等多種服務。

4 結束語

在核退役數字化仿真中研究人員行走最優路徑，完成了輻射場量和A-Star 最優路徑的耦合功能，并利用鼠標鍵盤等設備在核設施退役場景仿真系統動態交互起止點，可以滿足核設施退役三維場景任意兩點最優路徑的計算。此項研究在核設施退役人員輻射防護方案設計中有重要的參考價值。