基于馬爾可夫模型的電動重載卡車市場需求預(yù)測方法

李洪宇,付鳳平,張世科

(國網(wǎng)河北省電力有限公司營銷服務(wù)中心,河北 石家莊 050035)

0 引言

為了維護(hù)生態(tài)環(huán)境,減少對化石能源的消耗,很多車輛使用了綠色能源作為動力,如家用電動汽車、公交車等逐漸采用了電力動力,而且重載卡車進(jìn)入電動化時代。將電動重載卡車投入市場前,需要詳細(xì)了解客戶對該類產(chǎn)品的需求,并作出產(chǎn)品分析。

現(xiàn)有研究中,文獻(xiàn)[1]以TEI@I方法論為主要算法,設(shè)計了一個針對于航空客運(yùn)的產(chǎn)品框架,在分解EEMD時間序列的過程中,基于數(shù)據(jù)驅(qū)動對每個序列之間的關(guān)系進(jìn)行了的分析,并結(jié)合計量經(jīng)濟(jì)學(xué)等相關(guān)研究,設(shè)計了一套產(chǎn)品預(yù)測智能算法。將該方法應(yīng)用于電動重載卡車,其市場需求預(yù)測模型所得到的預(yù)測結(jié)果較為穩(wěn)定,但是該方法只能預(yù)測短時間內(nèi)的市場需求,在時間較長的市場需求預(yù)測中效果極差。文獻(xiàn)[2]為研究了水產(chǎn)品物流資源的合理配置,預(yù)測了該產(chǎn)業(yè)的冷鏈需求,基于RBF神經(jīng)網(wǎng)絡(luò)模型,設(shè)計了一套多元線性回歸算法,分別計算了冷鏈物流的各項需求分析,并對分析結(jié)果作出了綜合性的總結(jié),得到了一個誤差極小的預(yù)測模型。將該模型應(yīng)用于電動重載卡車市場需求預(yù)測模型中,可以得到較好的預(yù)測精度,但是其需要大量的數(shù)據(jù)支撐,計算效率較差。

為解決現(xiàn)有方法的不足,本文提出基于馬爾可夫模型的電動重載卡車市場需求預(yù)測方法,可有效預(yù)測電動重載卡車的市場需求,為電動重載卡車行業(yè)的規(guī)劃和發(fā)展提供幫助。

1 電動重載卡車市場需求灰色預(yù)測模型

根據(jù)已有信息對含有不確定因素的信息進(jìn)行模糊預(yù)測時,可以使用灰色預(yù)測方法。將所有移植數(shù)據(jù)相勾連,通過系統(tǒng)數(shù)據(jù)的發(fā)展趨勢進(jìn)行相關(guān)性規(guī)律的變動[3]。設(shè)置FM(1,1)模型作為數(shù)據(jù)隨機(jī)性的非負(fù)序列,此時的原始數(shù)據(jù)列為

式中:Y(0)為所有需要進(jìn)行預(yù)測的原始數(shù)據(jù)對;n為原始數(shù)據(jù)列的數(shù)據(jù)個數(shù)。隨著隨機(jī)性數(shù)據(jù)的增加,預(yù)測結(jié)果也會逐漸發(fā)生變化。此時,可以將增加處理后的原始數(shù)據(jù)預(yù)測結(jié)果用公式(2)表示

通過公式(2)可以得到一個新的數(shù)據(jù)隊,即Y(1)(n),i為常數(shù)。在累加數(shù)據(jù)的過程中,有一些關(guān)聯(lián)度很弱的相對誤差序列,需要在背景值中計算累減的生成序列[45]。此時可以將公式(1)中的原始序列以此展開,并代入最小二乘法進(jìn)行參數(shù)向量的辨識,得到

通過公式(3)可以計算關(guān)聯(lián)度的檢驗誤差,在預(yù)測值以及原始值的關(guān)聯(lián)中,如果大于0.5,則可以判定其為相對滿意的狀態(tài)。在后驗差的檢驗中,標(biāo)準(zhǔn)差的計算公式為

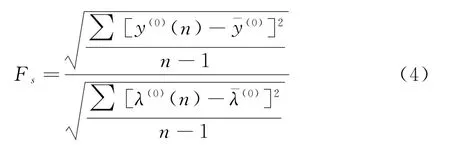
式中:Fs為最小誤差概率;λ(0)(n)為絕對誤差的相對標(biāo)準(zhǔn)差;為原始序列的標(biāo)準(zhǔn)平均值;為第1序列的相對標(biāo)準(zhǔn)差平均值[6-8]。根據(jù)公式(1)—(4)可以得到電動重載卡車市場需求灰色預(yù)測模型。

2 基于馬爾可夫模型修正誤差參數(shù)

在馬爾科夫模型中,存在多個轉(zhuǎn)移狀態(tài),而且每個被轉(zhuǎn)移狀態(tài)都需要依賴前一個狀態(tài),這樣就能夠得到一個具備模型連貫性的算法模型。由于灰度預(yù)測模型在隨機(jī)發(fā)展中的不確定性,需要通過馬爾可夫模型對誤差參數(shù)進(jìn)行修正,以提高市場需求預(yù)測的準(zhǔn)確率[9]。在馬爾科夫鏈中,有一個隨機(jī)數(shù)列,被集中于狀態(tài)空間中。此時的狀態(tài)空間被過去狀態(tài)的條件概率集中在同一個函數(shù),等待條件概率的轉(zhuǎn)移。假設(shè)此時的隨機(jī)變量均為一個完整數(shù)列,則這些條件概率分布的函數(shù)可以表示為

式中:Gx為當(dāng)前時段內(nèi)的變量狀態(tài);Gx+1為過去狀態(tài)下的變量分布概率;G0為第1序列的隨機(jī)變量狀態(tài);L為隨機(jī)變量分布;g為條件概率轉(zhuǎn)移狀態(tài)。在這樣的狀態(tài)轉(zhuǎn)移過程中,有一個具備N階不同參數(shù)的概率分布條件,可以將五元組表示出2個隱含狀態(tài)和1個直觀狀態(tài)[10]。此時的隱藏狀態(tài)中有1個初始時刻的概率矩陣,將這個初始矩陣作為隱藏狀態(tài)與觀察狀態(tài)的轉(zhuǎn)譯概率,可以得到馬爾可夫模型的轉(zhuǎn)移拓?fù)鋱D,見圖1。

如圖1所示,在轉(zhuǎn)移拓?fù)淠Ｐ椭?具備5個隱藏狀態(tài)的轉(zhuǎn)移概率,此時可以通過計算隱藏狀態(tài)與轉(zhuǎn)移狀態(tài)的相對矩陣,得到馬爾可夫模型的參數(shù)修正結(jié)果[11]。

圖1 轉(zhuǎn)移拓?fù)淠Ｐ?/p>

3 市場需求預(yù)測算法的構(gòu)建

通過以上方法獲得市場需求預(yù)測的參數(shù)修正結(jié)果后,可以據(jù)此設(shè)計多個基于馬爾可夫模型的電動重載卡車市場需求預(yù)測算法,算法流程如圖2所示。

圖2 算法流程

如圖2所示,在初始化參數(shù)集后,需要將所有時間坐標(biāo)節(jié)點全部遍歷,將其中的任意序列均插入到拓?fù)渚仃囍小Ｈ魧ふ业讲粚儆谟?xùn)練集的坐標(biāo)點,則重新初始化參數(shù)集。輸入所有已知的觀察點坐標(biāo),并計算市場需求的預(yù)測路徑。建立觀察者的灰度預(yù)測模型,以便通過時間推移的方式獲取更久遠(yuǎn)時間段的預(yù)測結(jié)果[1213]。判定預(yù)測指標(biāo)與實際數(shù)據(jù)的交集程度,此時若存在交集,則可以直接計算市場需求,并得到預(yù)測指標(biāo);若不存在交集,則需要初始化隱藏狀態(tài),并重新建立灰度預(yù)測模型,此時的預(yù)測模型可以計算時間段較長的市場需求。

4 市場需求量預(yù)測

4.1 確定影響因子及建立預(yù)測模型

文中設(shè)計了一種基于馬爾可夫模型的電動載重卡車市場需求預(yù)測方法,為測試該預(yù)測方法的準(zhǔn)確性,以2014—2017年電動載重卡車的市場銷售數(shù)據(jù)為基礎(chǔ),對2018—2021年的電動載重卡車市場銷售額進(jìn)行預(yù)測分析,并與已經(jīng)統(tǒng)計出結(jié)果的數(shù)據(jù)進(jìn)行對比,判斷該方法的準(zhǔn)確性[14]。2014—2017年電動載重卡車的市場銷售數(shù)據(jù)如表1所示。

表1 2014—2017年電動載重卡車銷售數(shù)據(jù) 輛

在現(xiàn)有電動載重卡車市場銷售量的研究中,對銷售額度影響最大的因素主要有貨物運(yùn)輸里程、公路運(yùn)貨量、區(qū)域人口數(shù)量、城市化率、電力消費總量5種因素。設(shè)置變量的選擇標(biāo)準(zhǔn),在不同的條件下,設(shè)相關(guān)系數(shù)Pf＜0.01,且不低于0.9。在多元線性回歸方程中,可以計算自變量與因變量之間的關(guān)系,此時的模型函數(shù)為

式中:yp為多元線性回歸模型的因變量參數(shù)值;b1、b2、bn為變量x1、x2、xn的系數(shù),此時n=1、2、3、4、5;ai表示5個影響因素之間的相關(guān)性[15]。通過SPSS統(tǒng)計分析方法將5種影響因素對電動載重卡車市場的需求進(jìn)行相關(guān)性驗證,可以得到矩陣

式中:E為5種影響因素對電動載重卡車的市場需求相關(guān)性權(quán)重指數(shù),i、j=1、2、3、4、5;u11為載重卡車的貨物運(yùn)輸里程;u22為單位里程公路的運(yùn)貨量;u33為區(qū)域人口數(shù)量;u44為城市化率;u55為電動載重卡車的電力消費總量。根據(jù)以上因素,建立電動載重卡車的市場需求量組合預(yù)測模型[16]。為了提高預(yù)測的精準(zhǔn)度,使用標(biāo)準(zhǔn)差法計算組合權(quán)重,設(shè)置指數(shù)平滑模型的多元回歸標(biāo)準(zhǔn)差分別為σi和σj。此時可以得到2個參數(shù)的計算公式

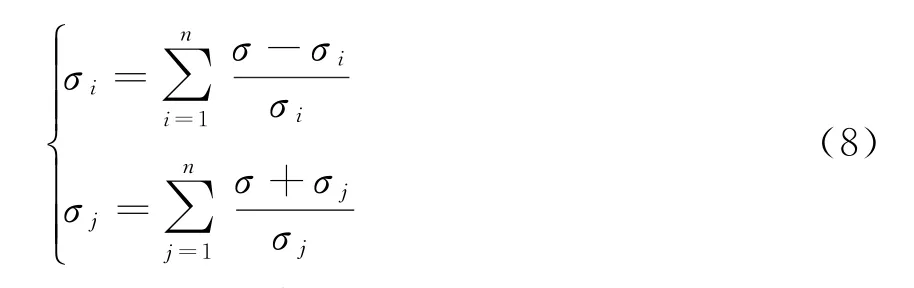
在計算2個參數(shù)的模型權(quán)重后,可以根據(jù)該組合權(quán)重,建立預(yù)測模型

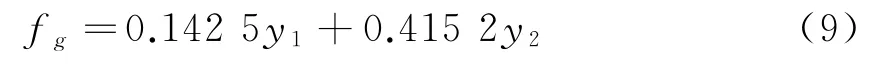
式中:fg為市場需求的預(yù)測值;y1為指數(shù)平滑預(yù)測值;y2為多元回歸預(yù)測值。根據(jù)該預(yù)測模型,可以直接預(yù)測該產(chǎn)品的市場需求。

4.2 市場需求量預(yù)測結(jié)果

結(jié)合上文中得到的預(yù)測模型,對比基于TEI@I方法論的預(yù)測模型以及基于RBF神經(jīng)網(wǎng)絡(luò)算法的需求預(yù)測方法,得到2018—2021年的電動載重卡車市場銷售額預(yù)測結(jié)果。獲取2018—2021年電動載重卡車市場的整體銷售額,作為該產(chǎn)品的實際需求量數(shù)據(jù),用以對比不同方法的預(yù)測差異值。2018—2021年電動載重卡車市場的整體銷售額如表2所示。

表2 2018—2021年電動載重卡車銷售額 輛

得到2018—2021年實際需求量數(shù)據(jù)后,計算預(yù)測結(jié)果與實際需求量之間的差異值,計算公式為

式中:λ為預(yù)測結(jié)果與實際結(jié)果之間的差異值;fx為該產(chǎn)品的實際需求量。通過以上公式計算,得到了不同方法的預(yù)測差異值,如圖3所示。

圖3 不同方法的預(yù)測差異值

如圖3所示,自2018年起,隨著時間點的后移,3種市場需求預(yù)測模型的差異值變化幅度在不斷增加,2018年的差異值相對平穩(wěn),但是時間越向后,差異值的變化趨勢就越明顯,且通過馬爾可夫模型得到的需求量預(yù)測差異值明顯小于其他2種方法。為了使結(jié)果更加直觀,將不同方法的需求量預(yù)測差異平均值以表格形式進(jìn)行展示,如表3所示。

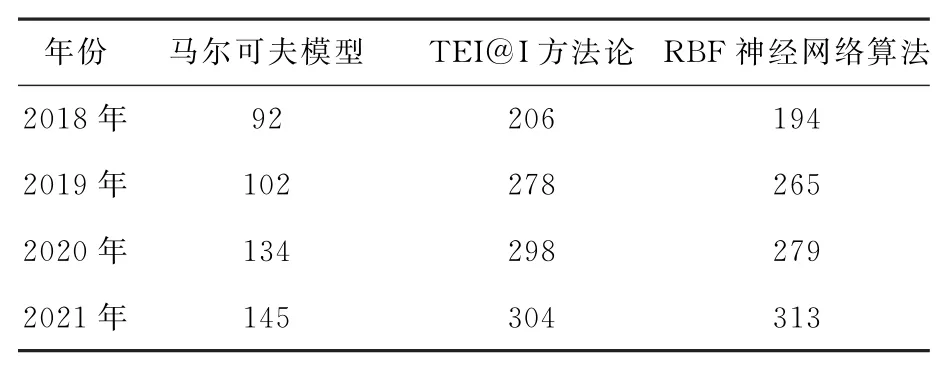
表3 不同方法的需求量預(yù)測差異平均值 輛

馬爾可夫模型的需求量預(yù)測差異平均值最高為145輛,而另2種方法的需求量預(yù)測差異平均值均超過300輛以上,由此可以說明本文設(shè)計的馬爾可夫模型的需求量預(yù)測差異平均值較低,對于電動重載卡車市場需求預(yù)測的準(zhǔn)確度更高。

5 結(jié)論

本文基于馬爾可夫模型設(shè)計了一個電動重載卡車的市場需求預(yù)測方法,構(gòu)建灰色預(yù)測模型,使用馬爾可夫模型對參數(shù)進(jìn)行優(yōu)化與改正,實現(xiàn)基于馬爾可夫模型的電動重載卡車市場需求預(yù)測方法的設(shè)計。并通過實驗驗證了設(shè)計方法能夠有效對2018-2021年內(nèi)電動重載卡車的市場需求進(jìn)行精準(zhǔn)預(yù)測,預(yù)測結(jié)果較為穩(wěn)定。雖然設(shè)計方法的預(yù)測精度較高,但是由于時間的限制,本文并未分析電動重載卡車市場存在的制約性,因此,在接下來的研究中,將著重分析市場需求預(yù)測過程中的影響因素,不斷完善設(shè)計方法,在預(yù)測過程中重點關(guān)注影響因素帶來的變化,提高預(yù)測方法的準(zhǔn)確性,以期為電動重載卡車未來的規(guī)劃與推廣提供一定的技術(shù)支持。