雙幅變孔徑篩面物料拋擲運動機理與優化

宋寶成，江海深，田祖織

1江蘇安全技術職業學院 江蘇徐州 221000

2中國礦業大學化工學院 江蘇徐州 221116

3國家煤加工與潔凈化工程技術研究中心 江蘇徐州 221116

4中國礦業大學機電工程學院 江蘇徐州 221116

振動篩是重要的礦物加工裝備，廣泛應用于各類選礦作業[1-2]。振動篩分工藝過程大多基于物料拋擲運動理論，采用拋擲指數衡量篩面上物料實現拋擲運動的能力[3]。Xiao J Z 等人[4]建立了一種具有擺動軌跡振動篩的拋擲指數分布函數，分析了顆粒落點位置的影響，認為拋擲指數是決定篩分效率的直接因素。Yin Z J 等人[5]在推導橢圓篩拋擲指數的基礎上分析了拋擲指數與物料運動速度的關系，認為合理的拋擲指數有助于物料輸送過程中的松散分層。劉德洋等人[6]推導了采用附加氣室空氣彈簧隔振的振動篩拋擲指數，通過改變振動頻率與振幅實現了拋擲指數的調節。

雙幅變孔徑篩面采用剛柔耦合的方式，兼顧剛性篩面與柔性材料篩面的優點。振動過程中，相鄰篩桿具有不同的振幅，可以獲得篩孔孔徑的周期性變化，對典型的堵孔現象能夠實現有效預防[7]。然而雙幅變孔徑篩面的幾何結構與振動方式較為復雜，傳統篩面的物料拋擲機理對其不再適用。為此，本文在建立雙幅變孔徑篩面顆粒受力模型的基礎上，得到了其拋擲指數分布函數；對其篩分過程進行了數值模擬，以篩分效率為指標，分別采用 GA、LRGA 與 GRNN 神經網絡結合的方法對拋擲指數各因素進行優化，以得到理想的拋擲指數分布，為相關產品的設計研發提供參考。

1 物料拋擲機理分析

雙幅變孔徑篩面結構如圖 1 所示。普通篩桿與篩框固連，與增強篩桿交替布置。增強篩桿末端通過橡膠塊與篩框柔性連結。在約束槽作用下，在x方向，增強篩桿振幅A2x與普通篩桿振幅A1x相同。

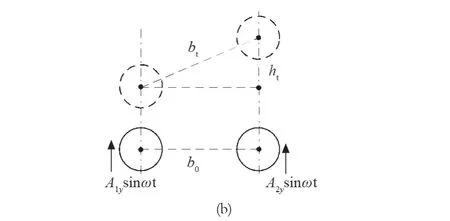
圖1 篩面結構與孔徑變化Fig.1 Structure of screen surface and variation of aperture

當篩桿質量m、橡膠塊剛度k與激振頻率ω滿足時[7]，在y方向，增強篩桿與普通篩桿振動同相，且振幅A2y＞A1y，孔徑dt產生周期性變化：

式中：b0為相鄰篩桿中心間距；r為篩桿半徑。

如圖 2 所示，以顆粒質心為局部坐標系O xpyp原點，yp為接觸點法向，xp為接觸點切向。全局坐標y指向豎直方向，x由入料端指向出料端。令普通篩桿與增強篩桿振動方向角分別為α1與α2，當xp與x的夾角與αi(i=1，2) 一致時 (如圖 2(a) 中xp')，篩桿對顆粒的支撐力N與振動方向垂直，篩面振動將無法得到N為 0 的平衡條件[8]，此處為顆粒被篩面振動作用拋起的左極限位置。當xp與重力方向一致時 (如圖 2(a) 中xp″)，篩桿對顆粒的支撐力N始終為 0，篩面振動對顆粒將不再產生作用，此處為顆粒被篩面振動作用拋起的右極限位置。將yp與y的夾角δ i稱為顆粒篩桿間的接觸偏角，所以拋擲指數存在的條件為δi∈(0，αi+0.5π)，其中i=1，2。

圖2 雙幅變孔徑篩面顆粒受力模型Fig.2 Force model of particle on double-amplitude variable-aperture screen

對滿足δi∈(0，αi+0.5π)(i=1，2) 的顆粒，顆粒受力情況如圖 2(b) 所示。分別建立xp與yp方向平衡方程為

式中：Ai為篩桿振幅。

令拋始角為φsi，由顆粒拋擲運動臨界條件N=0[8]可得

由此可知，振動強度Asi與拋擲指數AVi分別為

可見，由于A2x=A1x且A2y＞A1y，所以增強篩桿具有更大的振動強度 (Ks2＞Ks1)，且Ks1與Ks2均為定值，不隨顆粒與篩桿接觸位置的改變而改變。而拋擲指數與顆粒、篩桿間的接觸位置有關，在 (0，α i+0.5π) 范圍內，隨δi單調遞減。將δi=90°時的拋擲指數稱為頂點拋擲指數，由式 (6) 可知，使得相同δi條件下KV2＞KV1。

由于A2x=A1x，A2y＞A2y，所以，即增強篩桿的有效拋擲范圍大于普通篩桿。分別對α i、Ksi求偏導，由于Ksi大于 1[10]，可得

因此，對于普通篩桿與增強篩桿，振動方向角αi與振動強度Ksi越大，那么篩桿能夠使顆粒拋離篩面的有效拋擲范圍越大。

2 篩分數值模擬與參數優化

2.1 篩分數值模擬

圖3 所示為 EDEM 環境下雙幅變孔徑篩面離散元數值模擬模型。考慮到篩面寬度主要影響處理量，對篩分效率影響甚微，故篩面模型采用大長寬比參數 (1 010 mm×90 mm) 以提高數值模擬效率[11]。初始孔徑d=10 mm。利用顆粒填充技術模擬實際物料的復雜外形，以 0.6 kg/s 速率持續給料 (粒度小于d與大于d的物料比為 2∶3)，模擬單位面積處理量為 23.76 t/(h·m2) 的篩分過程；采用網格單元組 (Grid Bin Group) 獲取篩下物與篩上物的動態成分，直至獲得穩定的篩分效率η。物料密度為 1 300 kg/m3，篩桿密度為 7 800 kg/m3，其他物性參數如表 1 所列。

圖3 雙幅變孔徑篩面離散元數值模擬Fig.3 Discrete element numerical simulation on doubleamplitude variable-aperture screen

表1 篩分數值模擬參數Tab.1 Parameters of screening numerical simulation

由式 (5)、(6) 可知，當激振頻率固定時，影響雙幅變孔徑篩面物料拋擲效果的因素包括Aix與Aiy。在A1y與A2y協同作用下孔徑發生變化，為了便于分析該協同關系對篩分效果的影響，引入孔徑最大變化率ξ。由式 (1) 可知

取r=5 mm，b0=20 mm，進而可將篩分效果影響因素簡化為篩桿水平方向振幅 (因素A)、普通篩桿豎直方向振幅 (因素B) 及孔徑最大變化率 (因素C)。取振動頻率為 16.67 Hz，因素A、B分別具有 2.5、3.0、3.5、4.0、4.5 這 5 個水平值，因素C的 5 個水平值依次為 0.5、1.0、1.5、2.0、2.5。表 2 所列為相應正交試驗 (序號 1～25) 及補充因素水平組合 (序號 26～31) 數值模擬所得結果。

表2 數值模擬結果Tab.2 Numerical simulation results

表3 所列為極差分析結果，因素A、B、C在相應的水平值范圍內對指標η的影響顯著性由大到小依次為C、A、B，孔徑最大變化率對篩分效率影響最大。最佳因素水平組合為A3-B4-C4，該條件下 (序號 26) 的數值模擬結果為 92.724%，高于其他條件所得指標，證明了極差分析結果的可靠性。同時可以發現，指標η隨因素A、B、C均呈現先增大后減小的趨勢，適中的孔徑最大變化率有利于提高篩分效率。

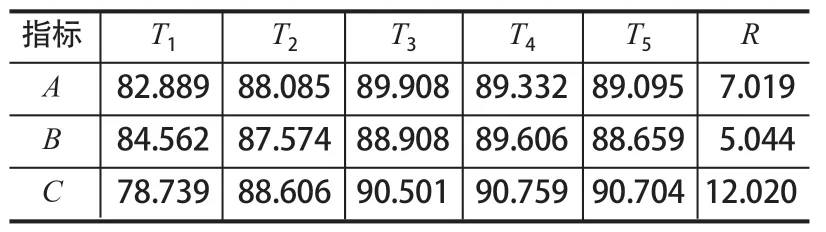
表3 極差分析結果Tab.3 Range analysis results

2.2 拋擲指數參數優化

取因素A、B、C為網絡輸入，指標η為網絡輸出，對數值模擬結果進行歸一化處理后，以序號 1～26 數據為訓練樣本，以序號 27～31 數據為檢驗樣本，采用 GRNN 神經網絡進行數據擬合，流程如圖 4 所示。分別采用 GA 與 LRGA[12]對 spread 進行優化，并對所得優化的 GRNN 神經網絡進行參數尋優，以得到指標η最大值對應的因素A、B、C值。

圖4 擬合與尋優流程Fig.4 Process flow of fitness and optimization

圖5 所示為分別采用相同算法參數 (種群規模，30；交叉概率，0.9；變異概率，0.01；進化代數，30) 的 GA 與 LRGA 進行 10 次擬合尋優所得結果。可以發現，采用 GA 所得結果較為離散，不能滿足優化需要；采用 LRGA 所得結果更為穩定，可信度更高。對 LRGA 所得尋優結果進行反歸一化處理，并以此參數進行數值模擬驗證，得到篩桿水平方向振幅Aix為 3.78 mm、普通篩桿豎直方向振幅A1y為 3.92 mm、孔徑最大變化率ξ為 2.1% 時，篩分效率為 93.576%，高于極差分析所得最佳結果。

圖5 尋優結果Fig.5 Optimization results

由式 (10) 可知，此時增強篩桿豎直方向振幅A2y為 6.83 mm，進而計算可得：普通篩桿振幅A1=5.45 mm，振動方向角α1=46.04°，增強篩桿振幅A2=7.81 mm，振動方向角α2=61.04°，普通篩桿、增強篩桿拋擲指數存在條件分別為δ1∈ (0，136.04°)，δ2∈(0，151.04°)。代入式 (5)、(6) 可得振動強度Ks1=6.089，Ks2=8.725，并得到篩桿拋擲指數分布優化結果：

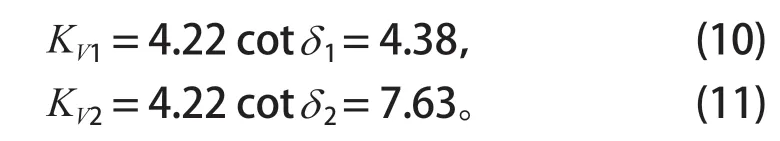
圖6 拋擲指數分布曲線Fig.6 Throwing index distribution curve

3 結論

(1) 普通篩桿與增強篩桿的振動強度均為定值，且增強篩桿振動強度較大。當顆粒篩桿間的接觸偏角δi∈(0，αi+0.5π) 時，拋擲指數存在，其值隨δi單調遞減。

(2) 雙幅變孔徑篩面篩桿有效拋擲范圍與振動方向角α i、振動強度Ksi正相關，增強篩桿的有效拋擲范圍大于普通篩桿。

(3) 拋擲強度的影響因素中，ξ對篩分效果影響最為顯著。當Aix=3.78 mm、A1y=3.92 mm、ξ=2.1% 時，可以獲得最高的篩分效率為 93.576%。

(4) 最佳拋擲指數分布條件下，普通篩桿與增強篩桿的頂點拋擲指數分別為 4.38 與 7.63，有效拋擲范圍分別為 (0，128.69°) 與 (0，147.52°)。