基于均質化等效的點陣夾芯板仿真方法
鄧夢,何敏,徐昉暉
(中國電子科技集團公司第十研究所,成都 610036)
引言
點陣材料是一種具有高孔隙率以及周期性結構的先進輕質多功能材料,可根據不同的受力環境實現每個微小單元的結構拓撲、單元數量與尺寸以及結構內局部的相對密度等參數的精確控制[1]。普遍情況下,點陣材料的相對密度僅是實體材料的十分之一,有利于設備的輕量化設計[2];同時,該類型材料還具有吸收環境噪音、減少沖擊響應、屏蔽電磁輻射和提供減振阻尼等多功能特性,目前已廣泛應用于航天航空飛行器、海軍艦船、汽車等領域[3-5]。
研究人員通常基于實驗方式對簡單點陣材料的各項力學特性進行研究。Geng針對金屬點陣材料與試驗機夾持困難的問題提出了非接觸式試驗方法,成功測得了選擇性激光熔煉制備的含菱形十二面體和BBC單元的AlSi10Mg點陣材料的彈性模量以及應力-應變關系曲線[6]。Xiao等通過單軸測試預測點陣材料的多軸屈服行為,提出了基于總應變能密度假設的點陣材料屈服準則[7]。Horn等利用四點彎試驗研究了基于電子束選區熔化技術的等截面桿、不同尺寸和不同相對密度的菱形十二面體點陣材料的力學特性[8]。Khalil等提出了一種基于極端統計量和Crossland HCF準則的方法,研究了基本單元拓撲結構在比例多軸載荷下對幾種類型單元結構抗疲勞性能的影響[9]。
然而,在點陣內部結構和外部尺寸先驗優化設計階段進行大量重復試驗與測試會帶來高昂的研制成本和漫長的設計周期,故完全基于實驗方法研究復雜點陣材料的打印過程和材料性能可行性較差。在眾多潛在的替代方法中,基于有限元方法的計算機輔助工程(CAE)技術可以顯著縮短研究周期并降低工作成本,目前已廣泛應用于點陣材料的疲勞分析[10]、優化設計[11-13]和生產制備[14]流程中。但目前的研究主要針對簡單點陣材料本身的制造工藝和宏觀特性,其結果對含有復雜點陣的零部件甚至整機設備的仿真分析與優化設計指導借鑒意義有限。
因此,本文采用了均質化等效的方法,將點陣材料均質化,對其材料特性進行等效處理,降低了含點陣材料的電子設備的仿真分析難度。
1 點陣材料均質化
點陣材料是由許多相同的點陣單元通過某種形式周期性的組合而成。點陣單元即胞元,點陣材料的均質化就是對胞元進行等效簡化。
1.1 均質化等效方法
對胞元結構進行均質化等效,等效體的應力等于胞元結構的平均應力,等效體的平均應變等于胞元結構的平均應變,如式(1)和式(2)所示。


而等效體的平均應力和平均應變的本構關系模型如式(3)所示。

式中:
De—胞元結構的等效剛度矩陣。
因此,胞元結構的均質化等效主要是求解胞元結構的等效剛度矩陣。

式中:
D—有限元的通用剛度矩陣。
各向異性的材料的剛度矩陣有21個未知變量、正交各向異性的材料的剛度矩陣有9個未知變量,而各項同性材料的剛度矩陣只有3個未知變量。
對于各項異性的胞元結構,等效剛度矩陣有21個未知變量,而且胞元結構通常尺寸很小,通過材料試驗的方式來獲取等效剛度矩陣的難度大。因此,采用有限元仿真分析的方法來對胞元結構的剛度矩陣進行等效。
在求解胞元結構的等效剛度矩陣De時,以胞元結構的應變為仿真分析的邊界條件,設計仿真邊界使應變的第i個元素((ii))中的值不為0、其余元素的值為0,此時,De的第i列De(i)與當前邊界狀態下胞元結構的應力響應的關系為:

因此,胞元等效剛度矩陣的第i列的值可通過式(6)求解。
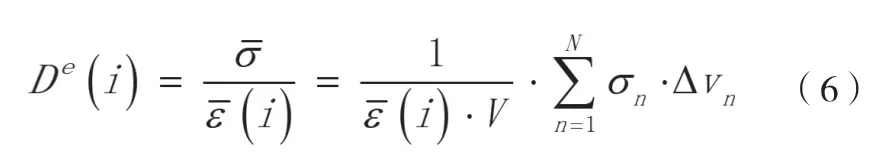
式中:
V—胞元結構的體積;
N—胞元結構網格單元的數量;
σn—第n個單元的平均應力;
△Vn—第n個單元的體積。
按上述方式依次進行六次求解,即可獲得胞元結構的等效剛度矩陣De。
1.2 均質化等效結果
本文中研究的胞元結構如圖1所示,選用的3D打印材料為AlSi10Mg,其材料特性如表1所示。

表1 AlSi10Mg材料屬性

圖1 胞元結構
按1.1節的方法對胞元結構進行等效處理,等效體的密度為924.35 kg/m3,等效剛度矩陣如表2所示。
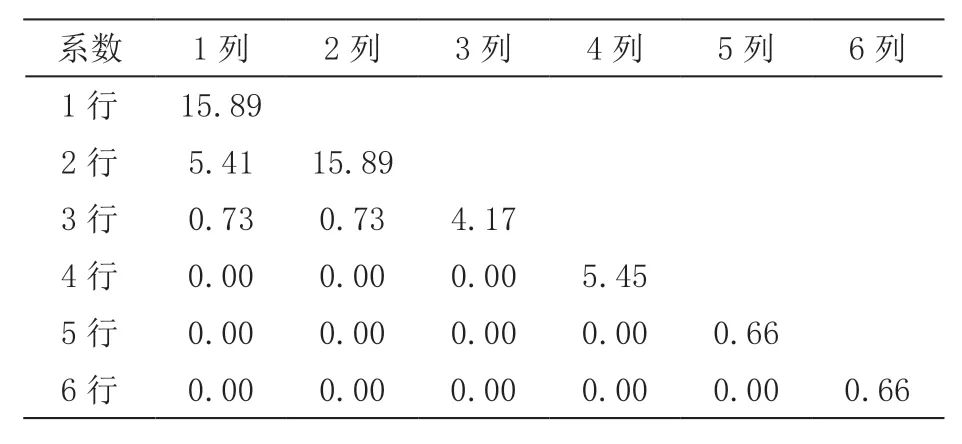
表2 等效剛度矩陣(GPa)
2 仿真及試驗方法
為研究1.2節求得的均質化等效結構能否準確模擬點陣材料在外界激勵下的真實響應,分別對其進行了試驗和仿真分析。
2.1 試驗設計
夾芯板主體為點陣材料,并在其表面打印一層厚度約為0.5 mm的實心層,使其形成一個封閉的整體,如圖2所示。
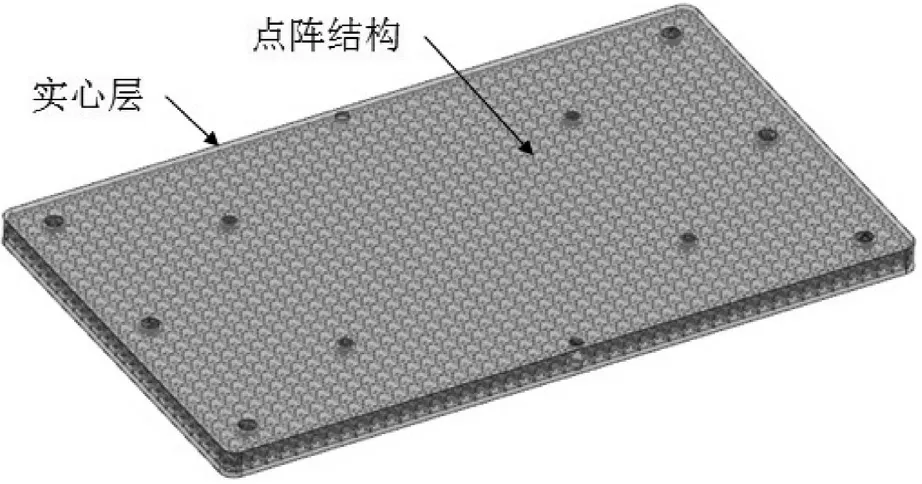
圖2 夾芯板模型
振動試驗激勵條件為隨機振動,激勵頻率范圍為(15~2 000)Hz、幅值為0.01 g2/Hz;試驗過程中采集夾芯板樣件的中心、長短邊中點三個典型位置的加速度響應信號,試驗件裝夾及傳感器布局如圖3所示。

圖3 夾芯板裝夾及傳感器布局
2.2 仿真設計
在對試驗板進行仿真分析前,需對試驗板進行等效處理,將點陣特征區域進行填充形成均質化層,如圖4所示。仿真分析時,均質化層采用AlSi10Mg均質化等效材料,實心層采用AlSi10Mg。兩部分模型之間通過節點耦合方式的進行連接。
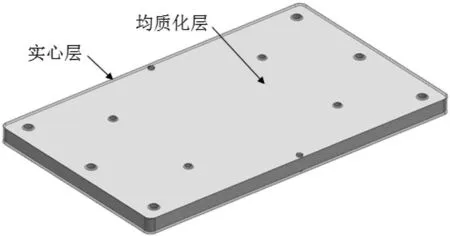
圖4 夾芯板模型簡化
為準確模擬設備在試驗中的響應,仿真時將實驗夾具也加入到仿真模型中,并采用梁單元模擬夾芯板和夾具的螺釘連接。通過夾具模型的安裝孔施加固定約束,作為隨機振動分析的激勵源,如圖5所示。仿真分析條件與振動試驗條件一致,阻尼采用軟件默認設置,即值為0.01的常數阻尼比。
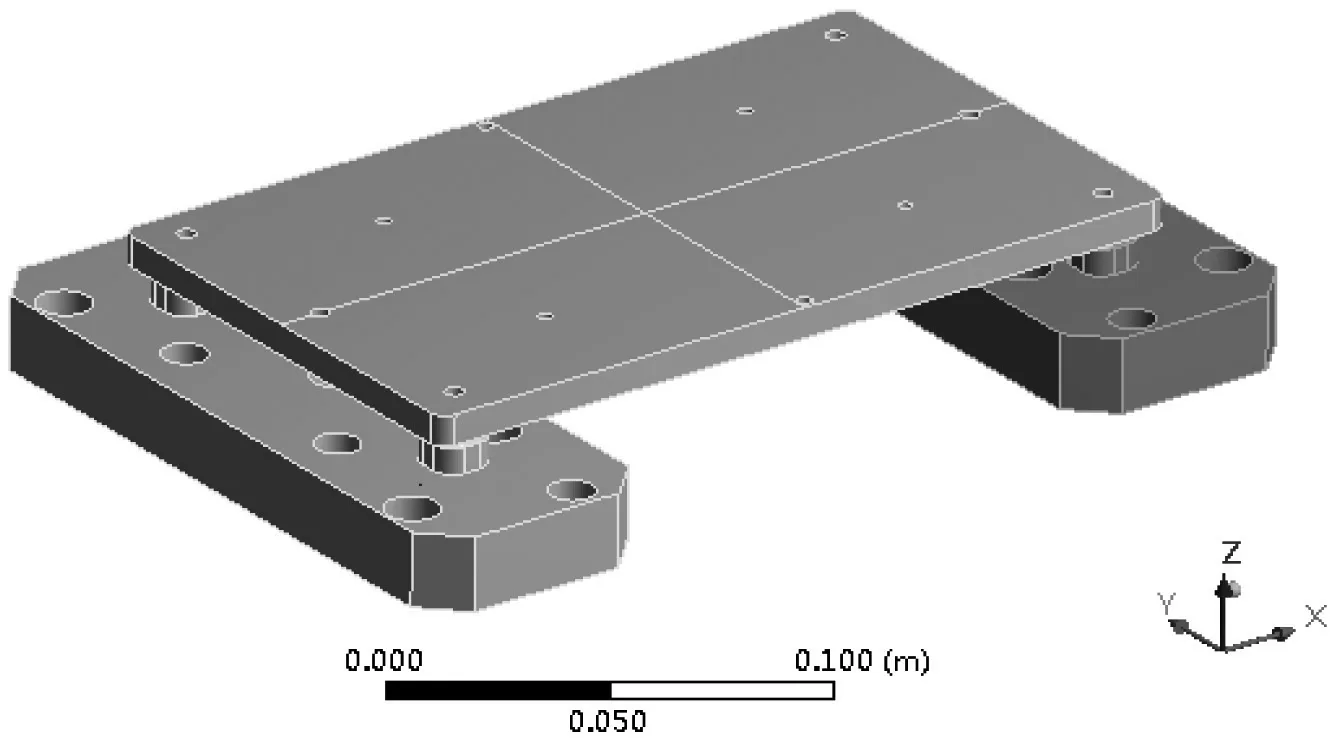
圖5 夾芯板仿真模型
3 結果分析
夾芯板隨機振動試驗的加速度測試結果如圖6所示。由圖6可知,測點3的響應結果與振動試驗條件基本一致;測點1和測點2的響應結果在698.4 Hz和1 302 Hz處有明顯的共振放大。
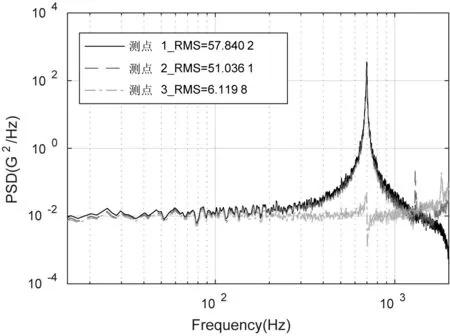
圖6 夾芯板測試結果
夾芯板的模態分析結果如圖7所示。在2 000 Hz的頻率范圍內夾芯板共有2階模態,固有頻率分別為701.7 Hz和1 406.4 Hz。與測試結果相比,仿真分析的前兩階固有頻率的偏差分別為0.43 %和7.96 %。
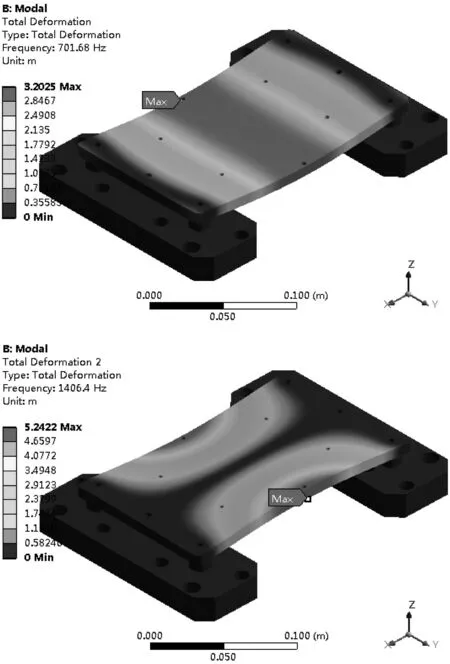
圖7 夾芯板模態分析結果
由圖6可知,僅測點1和2處有明顯的共振放大,因此,僅對比測點1和2的隨機振動條件的仿真及測試結果,如圖8和圖9所示。
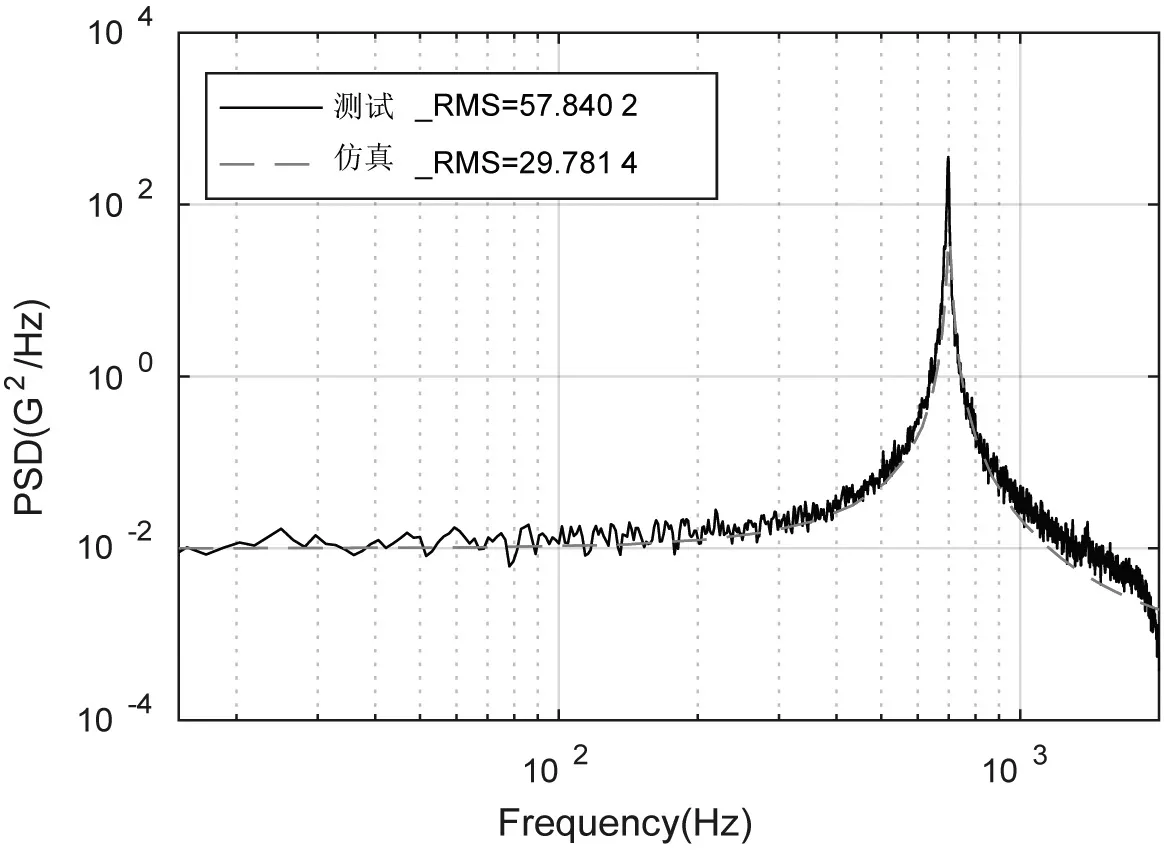
圖8 測點1仿真測試結果對比
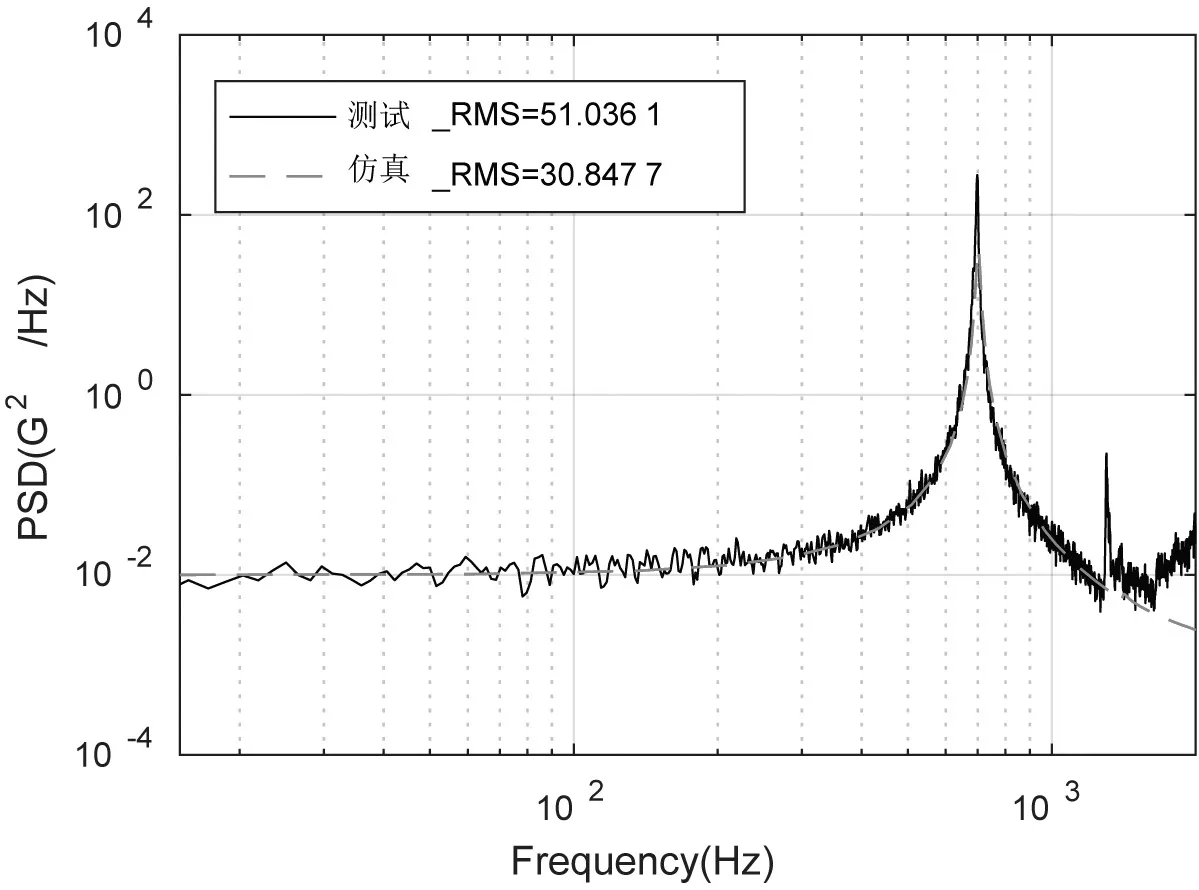
圖9 測點2仿真測試結果對比
由圖8和圖9可知,兩個測點的加速度響應的測試和仿真結果曲線的重合度較高,但其RMS值差距較大。這主要是由于仿真分析中設置的常數阻尼比的值與其實際值相差較大。通過修正仿真中的阻尼比參數,可對仿真結果進行修正,如表3、圖10和圖11所示。當阻尼比D=0.003 3時,測點1、測點2加速度響應的仿真曲線和測試曲線基本重合,且RMS值的相對誤差最大值分別僅為-9.34 %和6.43 %。
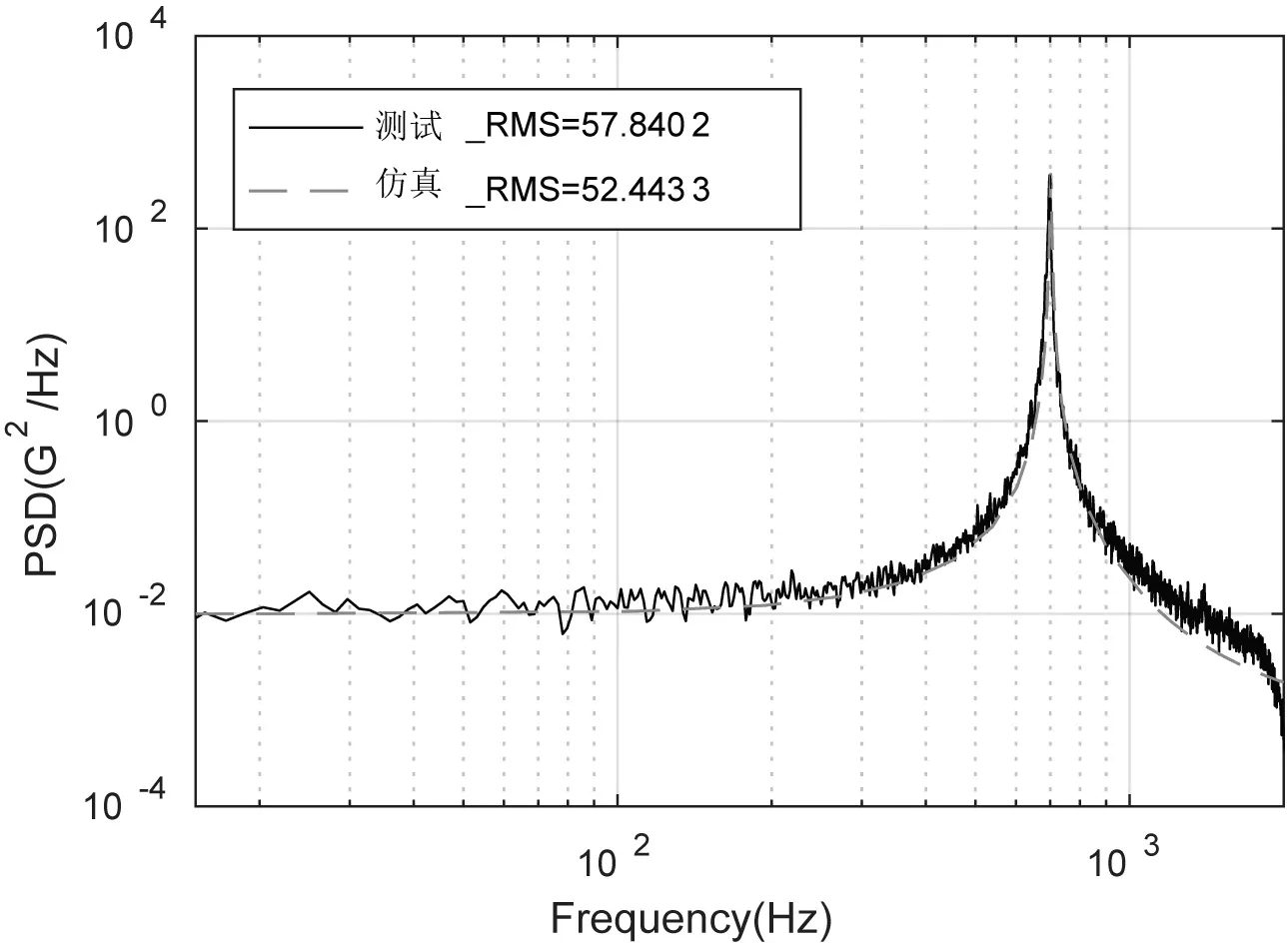
圖10 測點1仿真測試結果對比(阻尼修正后)
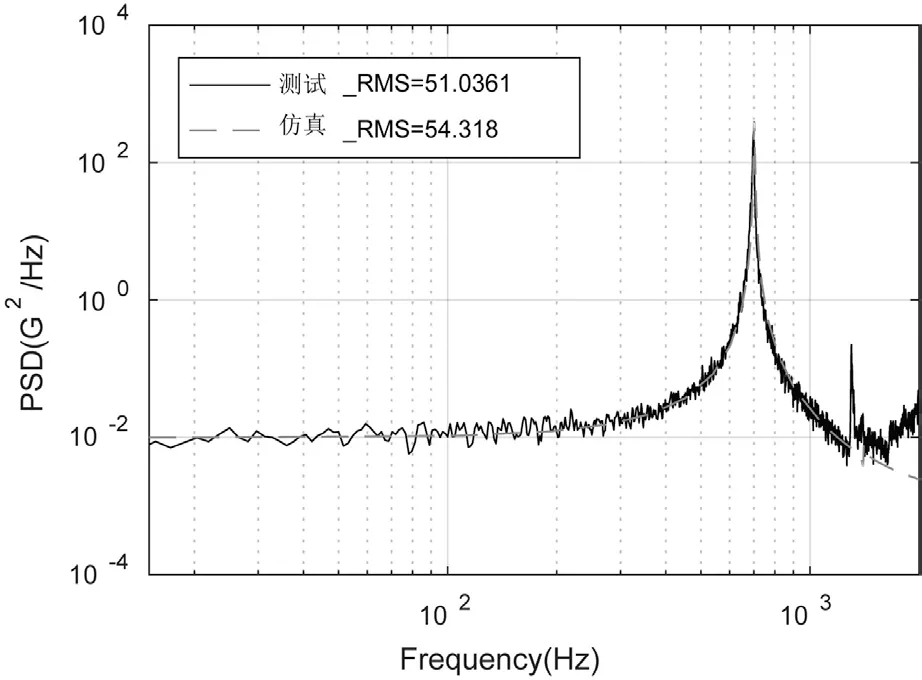
圖11 測點2仿真測試結果對比(阻尼修正后)
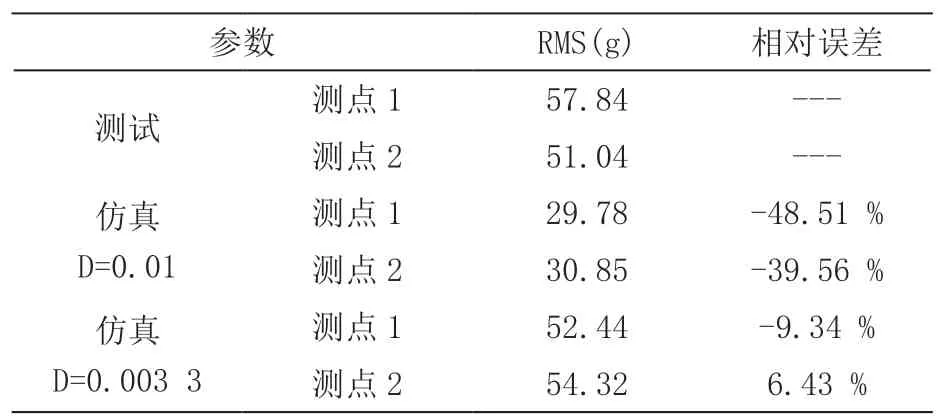
表3 仿真測試RMS值對比
4 結論
點陣材料是由許多相同的點陣單元通過某種形式周期性的組合而成,采用常規的有限元仿真分析方法,必然導致網格的節點數量過多而無法進行計算求解。本文提出了對點陣單元進行均質化等效的方法,使得含有大規模點陣單元的電子設備的有限元仿真分析成為可能。
對比仿真和試驗測試結果可知,采用均質化等效后的有限元分析固有頻率結果與試驗相比最大誤差為7.96 %,RMS值的最大誤差為-9.34 %,證明本文提出的點陣材料均質化等效方法在大幅降低了仿真難度的同時能很好地模擬其力學性能。

